引言

陆地表面温度(T_LS)是区域和全球尺度陆面过程中的一个关键因子，广泛应用于气候学、水文学、生态学等的研究。目前，科技工作者使用最多、最普遍的地表温度数据仍来自气象台站的地面温度(T_s)观测资料^[1]，它是对裸露土壤表面的观测温度。然而，土壤温度因土壤种类、土壤含水量等的差异，具有很强的局地性，而开展地温观测的台站又非常有限，若用常规的方法进行地温的空间插值，不可能获得满意的地面温度空间分布^[2]。

为了实现空间的拓展，不少学者开展了大量卫星反演产品与地面实际观测值的对比分析，试图利用遥感数据，来弥补观测台站的不足，获得满意的空间分布。如，廖顺宝等^[3]进行了NOAA-AVHRR资料反演地温与地面实测值的对比分析, 结果发现遥感反演的月最高地温与地面实测月最高地温的线性相关系数为0.86；刘晶淼等^[4]利用任意时刻AVHRR资料近似估计区域地表温度日较差的试验。侯英雨等^[6]利用卫星遥感资料估算空气温度。齐述华等^[5]研究了利用MODIS遥感影像获取近地层气温的方法，其精度约为+4 ℃。吴可军等^[6]在利用NOAA卫星资料分析城市热岛效应的过程中，采用9点平滑方法将T_LS转换为气温。有研究工作^[7-8]认为在一定的范围内，选择高植被覆盖度像元的T_LS作为气温的估计值是可行的。Prihodko和Goward等^[9]在假设气温与浓密植被冠层温度近似的基础上，结合可见光反射率和热辐射信息，得到植被完全覆盖下的T_LS可作为气温估计值的结论。过去的研究工作受卫星同步地面观测资料的限制，采用的绝大部分研究数据是地面观测日极值和假设温度日变化为正弦函数关系而估算的同步数据，极少有星、地同步观测数据。而这一点对于获得的是瞬时观测值的卫星数据而言，非常重要。本文利用近几年建立起来的自动气象观测台站信息，开展MODIS反演地表温度与准同步的空气温度和土壤表面温度的相关分析，建立基于卫星反演地表温度的同步土壤表面温度估算模型。

1 资料说明

四川盆地位于四川省的东部，外部轮廓可由广元—雅安—叙永—开江四市(县)的连线所构成，盆周为黄土壤的山区，以林地为主；盆中为紫色土壤的成都平原和丘陵区，水田、旱地及林地等零散分布其间。

1.1 资料选取

MODIS是EOS系列卫星的主要探测仪器，具有36个光谱通道(0.4~14.4 μm)，地面分辨率对不同波段分别为250 m，500 m和1 km。本文选用四川盆地绝大部分地方晴空的2005年3月5日、3月8日，2006年3月8日，2008年5月11日、5月19日共5轨Terra/MODIS数据。

自动气象观测站的空气温度和0 cm地温数据为每小时观测一次。地面观测数据是以气象站所在的卫星像元是晴空作为选取前提，挑选出不但有气温观测还要有地温观测的四川盆地气象站：2005年3月5日有41个，2005年3月8日有43个，2006年3月8日有72个，2008年5月11日有78个，2008年5月19日有67个。

1.2 资料处理 1.2.1 卫星资料

文中所用的Terra/MODIS的1B数据资料来自中国遥感卫星数据服务网(http://satellite.cma.gov.cn), 卫星白天经过四川盆地的时间集中在11：15—12：15，地表温度的反演采用分裂窗方法，由中国科学院遥感应用研究所的RSIS软件实现，地表温度空间分辨率为0.01°×0.01°。四川盆地气象观测台站所在的卫星像元均为混合像元，在1 km×1 km的范围内，有房屋、水田、旱地和林地等的多种组合，像元组分存在明显差异，像元下垫面不均匀。

1.2.2 地面观测资料

自动气象站观测数据只有整点观测, 要获得与卫星过境时间准同步的数据, 需要进行时间插值。温度随时间的日变化的关系可以用正弦关系表示^[10-11]，利用每个气象站的经纬度、观测日期，以及实测的最大、最小温度值，建立各自的谐波函数。然而，此方法的拟合值与实际每小时观测值比较结果表明拟合值并不理想，这是由于气温变化并非完全遵循正弦函数，还会受到当时云状、风等情况影响。考虑到分析数据是在11：00—12：00或12：00—13：00(Terra经过四川盆地时间)的1个小时内插值，而且是在日出以后、温度极大值出现以前的单调升温时段内，本文假设插值的1小时内温度变化是单调线性的，与卫星过境时间HH:MM准同步的地面气温与地温的获取便可采用下式进行插值，即

$ {T_{{\rm{HHMM}}}} = {T_{{\rm{HH}}-{\rm{1}}}} + \left( {{T_{{\rm{HH + 1}}}}-{T_{{\rm{HH}}-1}}} \right) \times MM/60 $

式中HH、MM分别代表卫星过境时的时、分；T_HH-1和T_HH+1分别是卫星过境时间前、后整点的观测温度。

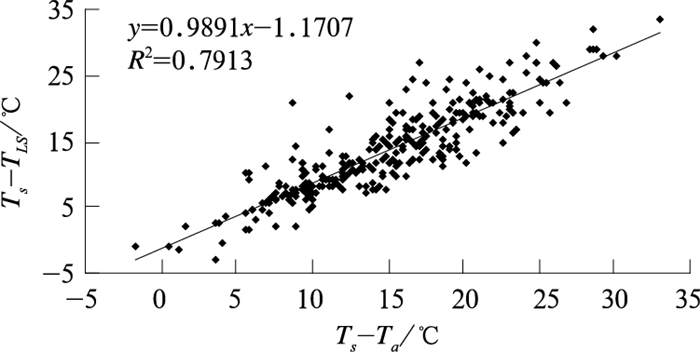
2 卫星反演地表温度与气温、地温的相关统计分析 2.1 相关分析

从表 1可见，将地面准同步观测的空气温度T_a、土壤表面温度T_s和卫星反演地表温度T_LS两两进行相关分析^[12]，发现总样本相关性很好，T_LS与T_s、T_LS与T_a、T_s与T_a的相关系数分别为0.834、0.854、0.864，都通过了0.001显著性检验。然而，非常遗憾的是它们都没有通过相关系数的稳定性检验^[13]，针对不同的卫星过境时间，相关系数相差甚大，特别是T_LS与T_a的相关系数2005年3月5日为-0.051，而2008年5月11日却为0.609，表现出极大的不稳定性。而相关系数是否稳定是统计模型效果好坏的关键问题，所以，T_LS、T_s和T_a两两不稳定的相关系数表明：简单利用卫星反演地表温度来估算气温、地温的精度不能得到保证，仅根据空气温度来进行地温的空间插值，会造成较大误差。究其原因，作者认为除了卫星像元地表温度的反演误差、以及卫星和地面观测非完全同步的原因外，地表状况的差异和尺度的不匹配是相关系数不稳定性的主要原因。众所周知，卫星反演地表温度是卫星像元尺度温度，对于非均匀下垫面，不同像元内组分的组成是不同的，地面气象观测只是针对其所在卫星像元内的观测点而言的，地温更是只代表像元内土壤组分的温度。依据Prihodko等^[9]的气温与浓密植被冠层温度近似的假设，那(T_s-T_a)与(T_s-T_LS)在一定程度上可反映像元内组分的差异，二者应该有较好的相关性。通过分析，果然发现(T_s-T_LS)与(T_s-T_a)存在显著线性相关(图 1)，且相关系数稳定，不论是总体样本还是不同卫星观测时间的子样本相关系数都达0.82以上，也都通过了0.001的显著性检验，判定系数R²=0.7913。(T_s-T_a)与(T_s-T_LS)的相关关系可表示为：

$ \left( {{T_s}-{T_{LS}}} \right) = 0.9891\left( {{T_s}-{T_a}} \right)-1.1707 $

(1)

2.2 地温的回归方程

依据T_LS、T_s和T_a三者的相关分析结果，假设T_s与T_LS、T_a有线性关系，从表 2给出的子样本和总样本的回归模型及检验参数可见，在一定程度上、一定精度范围内，假设是成立的，各回归方程在显著性水平α=0.01上具有显著性。从而，得到地温回归方程：

$ {T_s}^\prime = 0.648893{T_{LS}} + 1.000165{T_a} $

(2)

根据上述回归方程，利用气象站观测的空气温度和对应卫星像元的地表温度反演值，可以得到推算对应像元内的土壤表面温度。

2.3 误差分析

根据地温估算公式(2)，将估算地温与实际观测值进行比较，二者判定系数R²=0.9843, T_s′标准差为s=4.85 ℃。尽管误差看起来比较大，但是对于具有明显局地性、观测站点非常有限的土壤温度而言，文中采用遥感数据获取地温的方法还是具有一定应用价值的。

为了进一步提高区域地温的估算精度，可利用区域上的有限观测地温观测数据T_s和相应的估算值T_s′，建立地温订正经验线性回归方程

$ {T_s}^{\prime \prime } = a + b{T_s}^\prime $

(3)

之中T_s″为地温订正值。方程(3) 作为各网格点地温估计值的方程, 它可将偏差太大的估算值按其回归值加以订正。

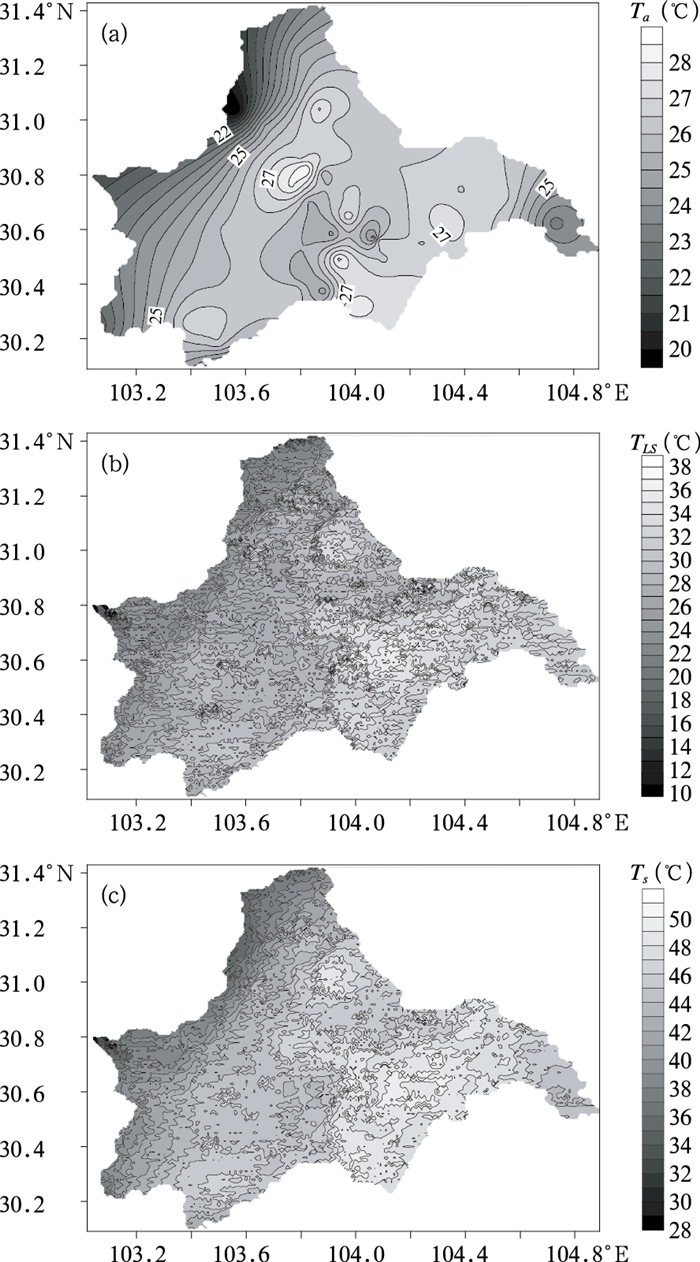
3 地温估算方程应用

选取2006年4月29日的自动气象站数据和Terra/MODIS遥感信息，进行成都市地表土壤温度的估算。成都市(30.09°~31.43°N、103.02°~104.89°E)以平原为主，空气温度的自动观测站点密度大，有44个自动气象站，空气温度可以通过插值方法获得较满意的结果，本文采用梯度距离平方反比法^[14]，将空气温度插值到与MODIS反演地表温度空间分辨率一致，在已知地表温度和空气温度的前提下，据方程(2)、(3) 就可推算出无实测地温观测资料的网点估算值，从而获得区域0.01度分辨率的土壤表面温度分布图 2。结果表明该数据在一定精度范围内，可为城市气象业务服务提供更加详尽的地面温度信息。

4 结论

通过对四川盆地准同步的T_LS、T_a、T_s两两相关关系分析，建立基于卫星反演地表温度和准同步空气温度的地温回归方程，得出以下结论。

(1) 对于非均匀下垫面，卫星反演地表温度与地表气温和0 cm地温的相关系数不稳定，各自的相关系数因卫星轨道时间的不同存在较大差异，缺乏稳定性。

(2) 地温与卫星反演地表温度的差值同地温与地表气温的差值之间存在既显著又稳定的线性正相关关系。

(3) 基于MODIS卫星反演地表温度和有限观测站点的气温、地温，可获得区域地温分布。统计模型在一定程度上、一定精度范围内，具有可行性，易于推广应用。

本文分析结果适用于四川盆地春季，其他季节、其他区域的适应性尚有待更多数据的验证。