2. 国家气象中心,北京 100081
2. National Meteorological Center, Beijing 100081
四川是一个多暴雨洪水的省份,新中国成立以来,局部或涉及数县乃至十多县的暴雨洪灾,几乎年年有之,因此,夏季的防汛,历来是四川省气象服务中的重要任务[1]。然而由于四川处于青藏高原东麓这一地形、地质结构最复杂的地区,其暴雨突发性强,时空分布不均匀[2-4],就连世界上最先进的预报方法、数值预报模式的产品对这一地区暴雨预报效果仍不能取得令人满意的结果[5]。集合预报方法的提出及其在数值模式预测中的成功应用被认为是大气科学领域的一项重要成就[6-7]。为适应预报服务的需要,四川省气象局于2004年在国内最早开展了区域集合预报的研究,并于该年9月投入业务运行[8],每日向预报员提供诸如降水平均、离散度、小雨、中雨、大雨、暴雨的降水概率等集合预报产品。面对海量的集合预报产品,如何取其精华,弃其糟粕,综合集成其优势,得到最优的样本预报结果,这是现今集合预报工作中薄弱的环节,国内可借鉴的方法很少[9-10]。随着各个学科的发展,尤其是数据挖掘和知识发现的研究进展,20世纪50年代产生的贝叶斯统计方法[11]受到了研究者的广泛关注[12-15]。作为一种统计方法,贝叶斯方法主张利用所有能够获得的信息, 包括样本和先于采样的信息, 进而对预报样本作出良好的推断与决策。Krzysztofowicz利用贝叶斯方法在水文预报中提出了贝叶斯概率水文预报理论[16],2007年,他将该方法引入数值预报的产品释用中,建立了BPF方法(Bayesian Processor Forecast)[17],目前,他正探索将贝叶斯方法与集合预报产品相结合的BPE方法(Bayesian Processor of Ensemble)[18],这是一种有价值的数值预报产品释用方法。本文在上述研究的基础上,利用贝叶斯方法,从四川预报员最关注的暴雨入手,探索从集合预报提供的暴雨的概率预报产品中,提取更好地体现暴雨概率预报价值的信息,进而建立四川省暴雨预警方法模型,促使暴雨的定量决策的结果更合理、更科学。
1 资料选取和贝叶斯方法概述 1.1 资料选取所用的资料有:
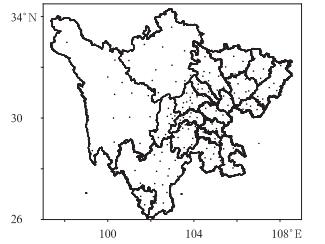
(1) 实况降水资料选取1951—2004年6—9月四川境内147个台站的逐日20:00时24小时累积雨量的整编资料,站点分布如图 1所示。
|
图 1 四川省境内147台站分布图 Fig. 1 The distribution of 147 observing stations in Sichuan Province |
(2) 集合概率预报资料选取西南区域中心区域中尺度集合预报系统提供的2008年6—9月预报时效为48小时的≥50 mm降水集合概率预报产品,产生概率预报产品的预报模式采用美国PSU/NCAR的高分辨率中尺度非静力MM5模式V3.4版,模式区域中心为:30°N、105°E,采用二重嵌套,粗网格区域是东亚区域,子域覆盖长江上游地区(图略)。粗网格格距为45 km,格点数为101×101,细网格格距为15 km,格点数为103×103,模式垂直方向为不等距的24层σ坐标。区域中尺度集合预报系统构造方案采用多物理扰动模式构造方案和异物理模态初始扰动场相结合的方法(详见文献[19])。客观分析采用修正的cressman香蕉型权重系数逐步订正分析方法,初值和边界条件利用东亚地区常规地面资料和探空资料,对背景场(T213全球格点场)进行再分析获得。≥50 mm的降水集合预报概率(P)的计算方法见式(1):
| $ P = (\sum\limits_{i = 1}^N {{P_i}} )/N, \begin{array}{*{20}{c}} {}&{{P_i} = 1\begin{array}{*{20}{c}} {}&{} \end{array}R \ge {R_0}}\\ {}&{{P_i} = 0\begin{array}{*{20}{c}} {}&{} \end{array}R < {R_0}} \end{array} $ | (1) |
式中P表示≥50 mm降水集合预报概率(假定每个集合预报成员是等权重的),N表示集合预报成员数(N=8),Pi表示每个成员24小时内≥50 mm降水预报值与实况暴雨的比较,R表示每个成员预报24小时降水量值,R0为24小时内的实况达到暴雨的降水量。
1.2 贝叶斯方法概述贝叶斯方法是多因子条件概率的一种综合方法。它适用于预报量事先有明确的状态,而预报因子事先没有划好状态,在预报分析过程中划定状态,这样一种预报问题。在贝叶斯方法中,任何具有不确定量的信息状态均可以用概率的形式来描述,随着新信息的增加,概率可以逐渐得到修正。也就是说该方法最主要的是确定所考虑的事件的概率分布,以及为了反映新信息而对该分布所做的修正。在气象应用中,对于暴雨这一类极端气象事件E的贝叶斯公式可以写为[10]:
| $ \begin{array}{*{20}{l}} {P(E/y) = \frac{{P(E)P(y|E)}}{{P(E)P(y|E) + P(\bar E)P(y|\bar E)}}} \end{array} $ | (2) |
式中y表示历史某个给定的时间段,P(y|E)表示在历史某个给定的时间段内暴雨E发生的概率,称之为似然函数,而P(E)和P(E)分别表示集合预报预报未来某个给定的时间段内暴雨的发生E和不发生E的概率,称之为先验概率,它独立于对历史某个给定时段内暴雨发生E和不发生E的概率,而后验概率P(E/y),即在对历史某个给定时段内暴雨发生概率被了解后暴雨的发生概率,当然,暴雨不发生E的后验概率P(E/y)也可由贝叶斯定理确定,或者从P(E/y)=1-P(E/y)中直接得出。这样,通过贝叶斯方法就将暴雨发生的气候概率与集合预报直接输出的>50 mm集合降水概率预报产品结合在了一起,二者的结合实际上就是“压制空报、容忍漏报”的过程,对空报“压制”的基础在于对于某地某一给定时间段内暴雨发生的次数是有限的,当大于或等于给定时间段内历史发生最大次数时,暴雨再发生的概率就变得很小了,对漏报“容忍”的基础在于,暴雨的发生是多种因素的结果,不能要求一种预报指标预报所有的暴雨。
2 基于贝叶斯方法的四川暴雨集合概率预警模型利用贝叶斯方法建立四川暴雨集合概率预警模型(以下简称贝叶斯模型),主要就是利用贝叶斯公式,计算后验概率的过程。
2.1 先验概率的选取被确定为先验概率的待选初始因子客观上有很多[10],但选取初始因子基本掌握以下几条原则:(1) 准确率高,从贝叶斯公式分析看,准确率高的初始因子对最终准确率有直接的影响;(2) 简单实用;(3) 稳定性好。
西南区域中心的中尺度区域集合预报系统于2004年投入业务运行,每天为预报员提供了多种集合预报信息,根据初始因子选取的原则,本文直接采用该系统利用式(1) 计算输出的>50 mm降水概率预报产品作为式(2) 中的先验概率P(E),模式输出是等距离格点的值,利用双线性插值法将暴雨概率格点值插值到147个需要预报的观测站点上。
2.2 似然函数的选取在贝叶斯统计方法中,新的信息(或新的统计样本)是通过似然函数进入分析过程的,似然函数就是为了反映新信息(或新样本)而对所考虑事件的先验概率分布所作的修正。客观上似然函数的选取有很多,如何有效地使用似然函数,发挥最佳作用,需要不断地加以探索。通过对1951—2004年6—9月四川境内147个台站的20—20时的实况降水资料的月暴雨最多日数和平均日数的统计(表 1给出了四川典型的代表站广元、绵阳、温江、雅安、南充、达州、自贡、内江、宜宾、乐山10站6—9月的月平均暴雨日数、月最多暴雨日数,其余137站的统计信息类似),可以看到像暴雨这样的极端天气事件,其发生日数的统计性质具有这样的一个特点,即在大量的观测记录中,月暴雨日数很少,最多天数一般也只有3~4天,也就是说针对暴雨这一单一事件,其发生与否当月其出现的日数有一定的关系,可以认为部分符合Bernoulli试验的要求[10],因而可以用Poisson分布的形式去描述它的概率特性,故选取暴雨发生当月其出现日数的概率来获取暴雨发生的似然函数。
|
|
表 1 四川典型代表站1951—2004年6—9月暴雨最多日数及平均日数(单位:日数/月) Table 1 The monthly maximum and average heavy rainfall days of Sichuan typical stations from June to Septemer during 1951—2004(units:d/mon) |
设x为所给定时段暴雨日数,则它具有如下的分布律:
| $ f(x) = {\mathit{\Lambda }^x}{{\rm{e}}^{-\Lambda }}/x!\;\;\;\;\;\;\;\;\;x = {\rm{0}}, {\rm{1}}, {\rm{2}}, \cdots, n $ | (3) |
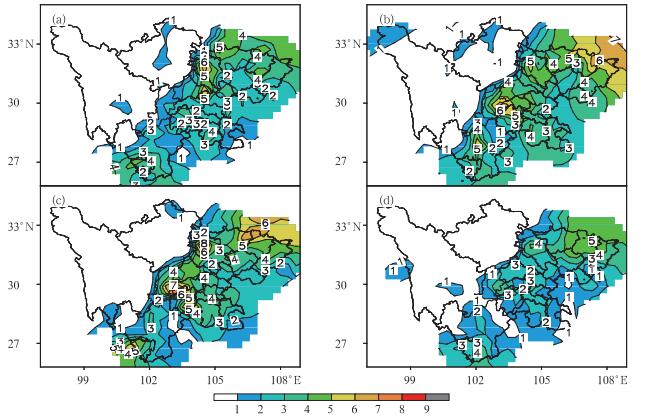
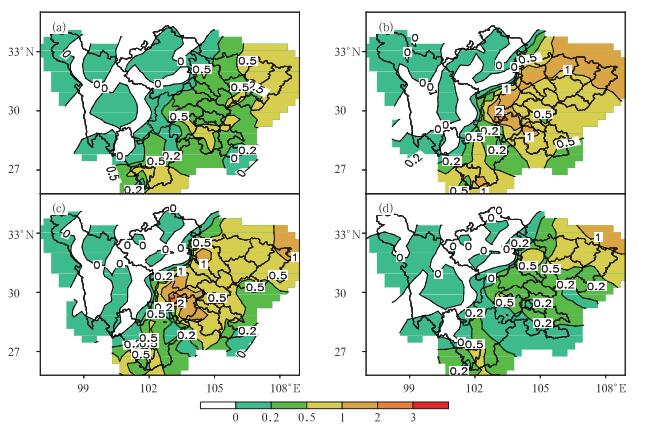
式中Λ是所给定时段暴雨日数的平均值。图 2给出了四川省147站1951—2004年6—9月暴雨最多日数。从图中可以看到6—9月盆地内站点月暴雨最多日数明显大于高原上的站点:盆地内站点上月暴雨最多日数可达9天(安县56194),而高原上月暴雨最多日数仅为5天;同为主汛期,但盆地内大多数站点7、8月的月暴雨最多日数多于6、9月。而从四川省月暴雨平均日数的分布图(图 3)可以看到6—9月盆地内的站点暴雨出现平均频数亦明显多于高原,需要特别指出的是,56384(峨眉)和56287(雅安)两站8月的月暴雨平均日数为3天,也就是说每年8月这两站几乎都有暴雨出现,不愧为“天漏”的称呼。
|
图 2 四川147站1951—2004年6—9月暴雨最多日数分布图(a)~(d)分别表示6—9月 Fig. 2 The distribution of monthly maximum heavy rainfall days of 147 stations in Sichuan Province from June to September during 1951-2004, (a) June, (b) July, (c) August, (d) September |
|
图 3 四川147站1951—2004年6—9月暴雨平均日数分布图(a)~(d)分别表示6—9月 Fig. 3 The distribution of monthly average heavy rainfall days of 147 stations in Sichuan Province from June to September during 1951-2004(a) June, (b) July, (c) August, (d) September |
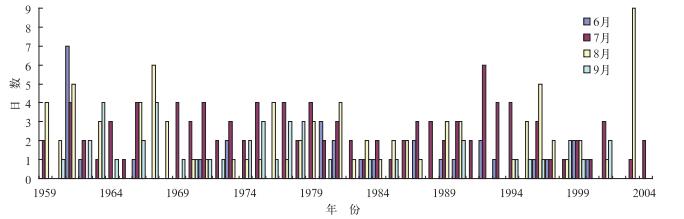
图 4给出了1959—2004年6—9月逐年月暴雨日数的56194站(安县)的时间演变图,从图中可以看到9月的多年月暴雨日数最多为4天,而8月为9天,而7月有10年达到4天或以上,9年达到3天,同时在这46年中,该站7月有暴雨出现的年份为40年,占86%以上,8月为33年,占到了71%,说明7、8月是安县暴雨日数最多的月份,同时也说明这两月也是安县暴雨发生概率极高的时段。
|
图 4 安县(56194)1959—2004年6—9月暴雨最多日数的时间演变图 Fig. 4 The time series of monthly maximum heavy rainfall days in Anxian County (56194) from June to September during 1959-2004 |
根据以上的统计事实,发现当预报站点当月的暴雨发生次数已经达到或超过月暴雨最多日数,那么该站当月再发生暴雨的概率肯定会减小。也就是说公式(3) 中的x是预报站点当月已发生暴雨次数tr和当月暴雨最多日数tm的函数,于是将公式(3) 改写为
| $ f(x) = {\Lambda ^{x(t)}}{{\rm{e}}^{-\Lambda }}/x(t)! $ | (4) |
式中x(t)=tm-tr,当Λ较小时,e-Λ可近似等于1,为讨论简单并减少计算量,对公式(4) 的计算结果做了如下简化处理:
f(x)=Λa×0.5b
公式(5) 中当预报初始时刻所在月份,tr=0,则a=0,b=0;当预报初始时刻所在月份,tr≠0,则a=1,若1≤tr≤tm且tr>Λ, 则b=1,若1≤tr<tm且tm<Λ, 则b=0, 若tr≥tm则b=-t。
2.3 后验概率的计算经过以上资料准备及技术处理后,先验概率和似然函数的分布就确定下来,那么根据公式(2) 后验概率的分布也随之确定。
为避免日常工作中冗长与繁琐的公式计算,通过采用过程化编程语言(VB6.0) 编制了一段计算机程序,将该项工作交由计算机完成,这样在实际应用中,只需要根据提示,仅输入几个原始数据便可获得结果,图 5为该计算过程的程序框架图。
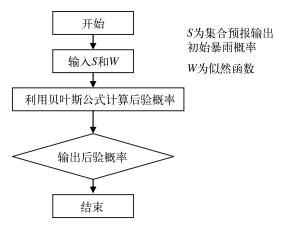
|
图 5 程序框架图 Fig. 5 The scheme of program frame |
在以上流程建立的基础上,对2008年6月1日至9月30日的暴雨预报引入了利用贝叶斯方法进行暴雨的概率预报的修正。
3.1 个例试验结果分析以2008年7月20日20时至21日20时发生在四川盆地的暴雨个例,对利用贝叶斯方法对集合预报暴雨概率预报产品进行的修正举例说明。
图 6a~6d分别给出了该时段的实况降水量、西南区域中尺度集合预报系统直接输出的暴雨概率预报产品(先验概率)、暴雨发生所在月份7月的四川多年气候概率(似然函数)以及经过贝叶斯方法修正后的暴雨概率(后验概率)。
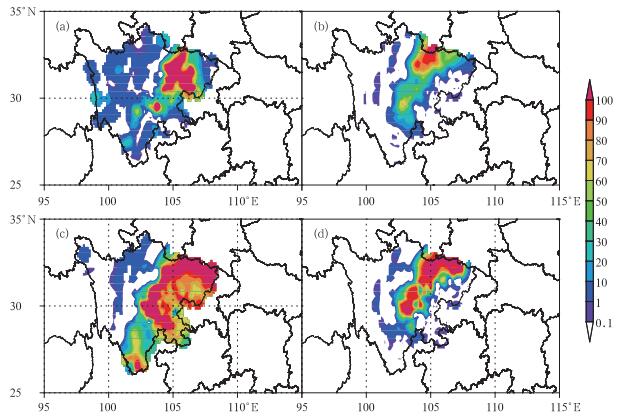
|
图 6 (a) 2008年7月20日20时至21日20时实况雨量(单位:mm); (b)初始概率,(单位:%);(c)似然函数(单位:%);(d)后验概率(单位:%) Fig. 6 (a) The rainfall from 20:00 BT 20 to 20:00 BT 21 July 2008 (units: mm), (b) initial probability(units:%), (c) likelihood function(units:%), (d) posterior probability(units:%) |
从图中可以看到:强降雨区主要位于盆地西部到中部,暴雨中心有两个,分别是江油288.4 mm、乐山280 mm(图 6a), 暴雨预报的概率大值区分别在盆地西北部和西南部的一小块区域(图 6b),图 6c给出了以暴雨气候概率作为修正因子的多年7月份出现暴雨初始概率分布情况,从图中可以看到在7月,整个盆地西部、北部是暴雨的多发区,从图 6d中可以看到,整个暴雨概率预报的大值区范围有所扩大,与图 6b比较,修订后的盆地北部的概率大值中心范围向盆地中东部扩大,修订前南充一带的暴雨概率预报值为20%,修订后其值增大为60%,整个北部暴雨中心向盆地中部扩展的这一事实与实况是基本相符的,乐山一带的暴雨概率大值中心,修订前其值为70%,修订后其值增大为100%,大大增强了暴雨预报可信度。
图 7给出了2008年7月19日20时的48小时后验概率预报与先验概率的偏差站点分布示意图,从图中可以看到,后验概率值比先验概率值既有增加,也有减少,其增加的概率的值大部分集中在实况暴雨区内,对先验概率中漏报的盆地中部的值增加比较明显,其增加幅度可达74%,大大增强了暴雨预报的可信度;对后验概率比先验概率减少的站点基本集中在未出现暴雨的地区,其减小幅度最大可达47%。
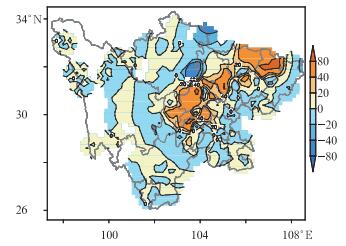
|
图 7 2008年7月19日20时48 h后验概率与先验概率的偏差分布图(单位:%) Fig. 7 The forecasting bias distribution between the posterior and prior probability of 48 h leading time started from 20:00 BT 19 July 2008 (units:%) |
也就是说,以暴雨发生当月其出现日数的概率来修订集合预报系统提供的暴雨概率预报,可以将原始暴雨概率预报产品中空报的概率大值中心值减小,漏报的地方给出一定的暴雨出现的信息,也就是前面所提到的“压制空报、容忍漏报”的概率修正过程,同样也就使得暴雨这一类发生概率极低的天气事件的历史统计信息与集合预报的模式预报结果有机地结合到了一起。
3.2 连续实验结果分析将2008年6月1日至9月30日四川省境内147个预报站点的48小时暴雨预报的后验概率最大值和先验概率最大值与相对应时段的暴雨个数(图 6)通过对比分析,可见:在整个连续试验时间段,四川省境内有11次比较强的暴雨过程(包括5次区域性暴雨过程)(图 8柱形),其对应的48小时集合预报的先验暴雨概率和后验概率的最大值峰值均与实况暴雨个数峰值吻合,没有漏报暴雨;同时在11次暴雨过程期间,暴雨的后验概率最大值均大于或等于先验概率最大值,说明经过贝叶斯模型修正后的暴雨概率预报能够增强可能出现暴雨的信号。在6月16—30日、7月12—14日、7月23—28日、8月16—20日、9月14—16日、9月18—21日、9月27日、9月30日,实况并未出现暴雨,而先验概率最大值却出现了较大峰值,但经过贝叶斯暴雨预报模型修正后其后验概率最大值的峰值均有所下降,如6月17日先验概率最大值为80%,经修正后其后验概率降为37%,说明利用贝叶斯方法修正后的暴雨概率预报能够减少暴雨预报的空报。
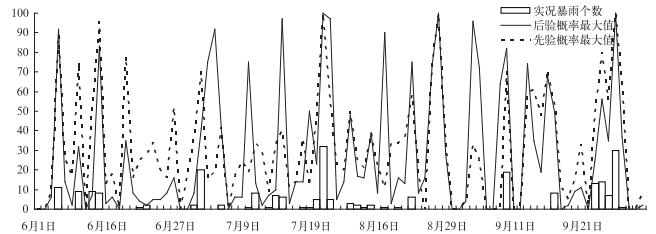
|
图 8 2008年6月1日至9月30日20时四川147个站48小时预报后验概率最大值与先验概率最大值与相对应时段暴雨个数对比图 (柱形为暴雨实况(单位:个);点线为先验概率,实线为后验概率(单位:%) Fig. 8 The comparison of 48 h leading time forecasting maximum posterior, prior probability and the number of real heavy rainfall stations from 20:00 BT 1 June to 20:00 BT 30 September, 2008 (column: the number of real heavy rainfall stations; dashed line: the prior probability, solid line: the posterior) |
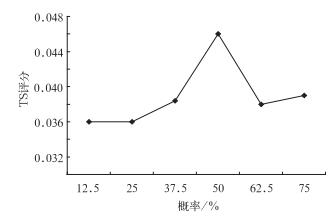
暴雨预报的概率确定后,如何准确的运用其信息来制作暴雨预报?图 9给出了通过反算2004—2007年6—9月西南区域中尺度集合预报系统提供的暴雨概率预报产品的后验概率后,分别取其值为≥12.5%、≥25%、≥37.5%、≥50%、≥62.5%、≥75%时预报暴雨的TS评分值,从图中可以看到,当集合暴雨概率预报值取到≥50%时,暴雨的TS评分值最高,达到了0.046。据此推断通过贝叶斯方法修正后的集合预报暴雨概率≥50%的可信度较大。分别对2008年6月1日至9月30日暴雨的先验概率和后验概率分别大于≥50%时判断有暴雨的结果进行TS和BS评分,表 2给出了其TS、BS评分结果。
|
图 9 2004—2007年6—9月集合预报系统暴雨概率预报产品的后验概率TS评分 Fig. 9 The Threat Score (TS) of the posterior probability of the EPS heavy rainfall probability from 1 June to 30 September during 2004-2007 |
|
|
表 2 2008年6—9月四川暴雨的先验概率和后验概率分别≥50%时判断有暴雨时的TS和BS评分 Table 2 The Threat Score(TS) and Bias Score(BS) of forecasting heavy rainfall by critical vaule of prior and posterior probability over 50% |
从表 2可以看到,当均取≥50%的暴雨概率预报值来进行有暴雨预报时,经过贝叶斯方法修正后的暴雨概率预报产品(后验概率)的TS评分值大于未经过处理的区域中尺度集合预报系统直接输出的概率预报产品(先验概率)的TS评分值,同时后验概率的BS评分也小于先验概率的BS值。说明利用贝叶斯方法修正后的暴雨概率预报不仅能够提高暴雨预报的准确率,同时也能在一定程度上减少暴雨预报的空报率,再次证明了利用贝叶斯方法进行暴雨概率预报修正的本质就是“压制空报、容忍漏报”。
4 小结与讨论贝叶斯概率理论为解决从集合预报产品海量信息中提取对暴雨预报有效的信息提供了数学依据, 其重要性已远远超出了它的特定范围。本文详细地描述了利用贝叶斯方法对集合暴雨概率产品的释用过程,并对其修正前后的结果进行了对比分析。得出以下几点结论:
(1) 对于可以取得的暴雨这一类极端天气的预报资料总是有限而在日常的预报中又必需经常做出预测的问题,应用贝叶斯方法有特别的意义,其核心在于将暴雨这一类发生概率极低的天气事件的历史统计信息与集合预报的模式预报结果进行有机的结合。
(2) 利用贝叶斯公式得到的更新概率分布将改进当前暴雨出现的概率分布; 不仅可以有效地增强暴雨可能出现的信号,直观地展示暴雨可能发生的区域,同时还能有效地减小暴雨预报空报的可能性,也就是“压制空报、容忍漏报”。
本文对贝叶斯方法的使用,仅仅采用了集合预报产品中的暴雨概率产品与暴雨发生当月其出现日数的概率的结合,其他诸如暴雨的离散度、各成员暴雨预报量值、对流层低层的相对湿度、温度等均对暴雨预报有指示意义,可以当作新的信息利用贝叶斯的方法不断地修正暴雨的概率预报,但这需要进一步的深入研究。
四川省短期天气预报手册[G]. 1986, 下册: 1-4.
|
康岚, 冯汉中, 屠妮妮, 等, 2008. 一次川渝大暴雨的中尺度分析[J]. 气象, 34(10): 40-49. DOI:10.7519/j.issn.1000-0526.2008.10.006 |
陈静, 李川, 谌贵珣, 2002. 低空急流在四川"9.18"大暴雨中的触发作用分析[J]. 气象, 28(8): 24-29. DOI:10.7519/j.issn.1000-0526.2002.08.005 |
顾清源, 肖递祥, 黄楚惠, 等, 2009. 低空急流在副高西北侧连续性暴雨中的触发作用[J]. 气象, 35(4): 59-67. DOI:10.7519/j.issn.1000-0526.2009.04.008 |
陈静, 矫梅燕, 李川, 2003. 青藏高原东侧一次β中尺度对流系统的数值模拟[J]. 高原气象, 22(增刊): 90-101. |
Sivillo J K, Ahlquist J E, Toth Z, 1997. An ensemble forecasting primer[J]. Weather and Forecasting, 12(12): 809-817. |
毛恒青, 王建捷, 2000. 集合预报业务使用现状和趋势[J]. 气象, 26(6): 26-29. DOI:10.7519/j.issn.1000-0526.2000.06.006 |
冯汉中, 陈静, 何光碧, 等, 2006. 长江上游暴雨短期集合预报系统试验与检验[J]. 气象, 32(8): 12-16. DOI:10.7519/j.issn.1000-0526.2006.08.002 |
马清, 龚建东, 李莉, 等, 2008. 中尺度集合预报的二阶矩离散度订正研究[J]. 气象, 34(11): 15-21. DOI:10.7519/j.issn.1000-0526.2008.11.003 |
马清, 龚建东, 李莉, 等, 2008. 超级集合预报的误差订正与集成研究[J]. 气象, 34(3): 42-48. DOI:10.7519/j.issn.1000-0526.2008.03.007 |
张军, 葛军, 田俊杰, 等, 1998. 概率天气预报及其应用[M]. 北京: 气象出版社, 115-126.
|
罗海飞, 吴刚, 杨金生, 2006. 基于贝叶斯的文本分类方法[J]. 计算机工程与设计, 27(24): 4746-4748. DOI:10.3969/j.issn.1000-7024.2006.24.040 |
张洪刚, 郭生练, 刘攀, 等, 2005. 基于贝叶斯方法的实时洪水校正模型[J]. 武汉大学学报(工学版), 38(1). |
尹力峰, 李锰, 宋立军, 2001. 贝叶斯模型在房屋震害预测中的应用[J]. 高原地震, 13(4). |
王秀梅, 2000. 用贝叶斯公式分析风险决策与信息的价值[J]. 价值工程, (3): 38-39. |
Krzysztofowicz R, 1985. Bayesian model of forecasted time series[J]. Water Resources Research, 21(5): 805-814. |
Krzysztofowicz R, 2008. Probabilistic Forecasts from the National Digital Forecast Database[J]. Weather and Forecasting, 4(27): 270-289. |
Krzysztofowicz R. http://www.faculty.virginia.edu/rk/BPE.
|
陈静, 李川, 冯汉中, 等, 2004. 青藏高原东侧"2003[J]. 高原气象, 23(增刊): 6-13. |
 2010, Vol. 36
2010, Vol. 36 