引言

由于大气是一个对初值敏感的、高度非线性的动力系统，所以像决定性数值预报方法那样，仅用众多可能的预报状态的一种来描述大气未来的状态是不够科学的，更合理的方法是以概率的形式来认识大气预报状态，而对所有可能的预报状态及这些预报状态的概率分布进行预报，这种预报方法就是集合预报。集合预报为解决单一确定性预报存在不确定性的问题提供了一条新的途径。通过对集合预报产品解释应用方法的研究，能提高对极端性天气的预报能力和对危险性天气的防御能力，为预报员的预报决策提供有效的、实用的预报结果，这些成果将具有应用价值。目前发达国家都开展了集合预报业务，且多种集合预报产品已应用到实际业务中，其中以欧洲中心的集合预报产品最为丰富，包括离散度图、要素概率图、邮票图、概率烟羽图等^[1-4]，在数值预报产品中集合预报产品占60%。我国对集合预报产品的研究也越来越受到重视，中国气象局的中期集合预报也实现了业务化，但对集合预报的解释应用工作远远不够，产品数量还不够丰富，解释应用方法还不够完善。目前相关方面的学术论文也很少，皇甫雪官^[5]对集合预报结果进行了Talagrand概率分布、离散度、BS评分、命中率以及空报率的统计检验。毛恒青等^[6]采用面条图、温度变化趋势图等对集合预报产品进行了解释应用。本文将针对几种集合预报产品应用作进一步的研究，并将其应用到“麦莎”台风的预报中，以期提高对极端性天气的预报水平，使集合预报结果更加客观^[7-10]。

1 台风麦莎和试验方案简介

2005年7月31日至8月9日，0509号台风麦莎影响了我国东部沿海和华东地区，使我国出现大范围暴雨和大风天气，此次台风是继1997年11号台风后，近8年来对我国影响最严重的台风之一，给人民的生命财产造成很大损失^[11]。

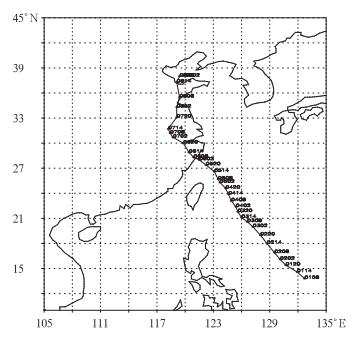
台风麦莎于2005年7月31日在菲律宾以东洋面上生成，在东南气流引导下向西北方向移动，8月3日02时(北京时间，下同)加强为台风，8月6日03时40分在浙江玉环登陆，登陆时中心附近最大风速45 m·s^-1，然后向西北方向移动，8月6日，江苏省受到“麦莎”前锋的影响，普降暴雨，8月6日22时15分后，“麦莎”影响安徽，8月7—8日，“麦莎”席卷山东，8月7日晚，天津出现2005年首次风暴潮，8日出现一次大范围的强降水天气。9日07时10分在辽宁省大连市龙王塘镇再次登陆。台风登陆后开始一直沿西北方向移动，在7日08时，当其移动到31.2°N、118°E附近时，又转为向东北向移动一直经过山东半岛到达渤海湾^[12-14](见图 1)。

采用T106L19全球谱模式和增长模繁殖法对本次台风过程制作了集合预报，繁殖循环初始扰动取为T106L19模式24小时预报均方根误差乘在[-1, 1]之间均匀分布的随机数；繁殖模采用成对繁殖的方法生成，即繁殖模定义为加扰预报与减扰预报之差的1/2；繁殖循环周期同客观分析周期取为6个小时；总时间繁殖为3天；前人研究表明^[15-16]，在集合预报中，采用8个集合成员求平均已能完成集合平均对预报精确度改善量的主要部分，增加集合成员数有利于提高集合预报效果，由于计算条件限制，在此集合成员取为13个，其中一个控制预报，6个加扰预报和6个减扰预报。预报时效为10天，前5天为每6小时输出一次结果，后5天为每12小时输出一次结果，共有31次结果。

2 集合预报产品的应用 2.1 形势场分簇

根据集合预报各成员的演变趋势，可以把所有成员预报的结果分成几簇，使每一簇的变化趋势十分相似，每一簇的平均场就是形势场分簇图。这是有效提取集合预报产品有用信息的方法之一。该产品可以为预报员提供几种类型的形势场演变趋势，并给出每种类型可能出现的概率大小。欧洲中期天气预报中心(ECMWF)采用差值均方根分簇法进行分簇，该方法将各成员之间500 hPa高度场的差值均方根作为衡量它们之间距离大小的标准，分类时选定欧洲区域，是以5~7天的预报场作为分簇的基础^[6]。我国现在采用的分簇法是离散距离分簇法，该方法以各成员对集合平均的离散程度大小进行分类，采用30°~50°N、110°~130°E范围内500 hPa高度场96小时预报资料作为分簇基础^[17]。具体做法如下^[6]：

设每个预报成员在选定区域内的格点高度值分别为H_ij(i=1, 2, …, N, j=1, 2, …, M)，其中i为预报成员序号，j为选定区域格点的序号。则区域内各点上高度的平均值为：

$ {\overline H _j} = \sum\limits_{i = 1}^N {{H_{ij}}} /N $

(1)

各成员在各点上的距平值为：

$ \Delta {H_{ij}} = {H_{ij}}-{\overline H _j} $

(2)

区域内各成员的平均距平值为：

$ {\overline {\Delta H} _i} = \sum\limits_{j = 1}^M {\Delta {H_{ij}}} /M $

(3)

因此，在该区域内所有成员的离散距离定义为：$ L = \max ({\overline {\Delta H} _i})-\min ({\overline {\Delta H} _i})$。

根据离散距离大小，将预报成员分为如下3簇：第一簇：$ {\overline {\Delta H} _i} \le-L/4$；第二簇: $ -L/4 < {\overline {\Delta H} _i} \le + L/4$；第三簇:$ + L/4 < {\overline {\Delta H} _i}$。

2.1.1 方差分析在离散距离分簇法中的应用

采用离散距离分簇法，分簇基础的确定是分簇成功与否的关键，目前没有一个统一的确定方法，前面已经提到离散距离分簇法中以往取第96小时的预报场作为分簇的基础。为了找出一种更合理确定分簇基础的方法，我们将方差分析引入离散距离分簇法中。方差分析是通过对试验数据的分析来辨别矛盾主次的一种数学方法，方差分析中的F统计量反映了簇间差异与簇内差异之比，若F值越大，则说明同簇的样本数值的离散程度小，而不同簇的样本之间数值离散程度大，则可以说明分簇越显著。计算F统计量公式为^[18]：

$ F = \frac{{\overline {{S_1}} }}{{\overline {{S_2}} }} $

(4)

其中：${\bar S_1} = \frac{{{S_1}}}{{a - 1}},{\bar S_2} = \frac{{{S_2}}}{{\sum\limits_{i = 1}^a {{b_i} - a} }}$，而S₁=Q-P，S₂=R-Q，P、Q和R的计算方法如下：

$ P = \frac{1}{{\sum\limits_{i = 1}^a {{b_i}} }}{(\sum\limits_{i = 1}^a {\sum\limits_{j = 1}^{\mathop b\nolimits_i } {{y_{ij}}} } )^2} $

(5)

$ Q = \sum\limits_{i = 1}^a {\frac{1}{{{b_i}}}(\sum\limits_{j = 1}^{\mathop b\nolimits_i } {{y_{ij}}{)^2}} } $

(6)

$ R = \sum\limits_{i = 1}^a {\sum\limits_{j = 1}^{{b_i}} {{y_{ij}}^2} } $

(7)

其中，i表示簇号，范围从1到a；b_i表示第i簇内的样本数；j表示簇内样本号，范围从1到b_i；y_ij表示第i簇第j号样本。S₁的自由度为a-1；S₂的自由度为$ \sum\limits_{i = 1}^a {{b_i}-a} $。

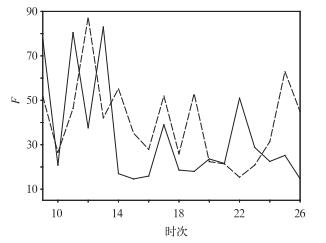
以8月2日及8月4日起报的850 hPa高度场的10天预报为例，分簇基础的计算区域为15°~50°N、90°~150°E，考虑到预报时效为中期时段以及T106模式的预报效果，将3~8天模式输出的18个时次的集合预报结果作为分簇的基础，按以上公式计算F值。图 2为F值曲线图。分析图 2可以看出，对3~8天的预报结果，8月2日起报的F最大值出现在第66小时(即模式第12个时次的输出结果)；8月4日起报的F最大值出现在第72小时(第13个时次)。也就是说对于这两天的预报以66小时和72小时作为分簇基础进行分簇时，可以使簇内成员相似性最大，簇间成员的相似性最小。

2.1.2 分簇结果分析

表 1给出的是以第66小时预报场作为分簇基础，对8月2日起报的10天预报的850 hPa高度场分簇的结果。

8月2日起报是提前4天对台风登陆进行预报，模式控制预报及集合平均预报的结果是台风中心都不会登陆我国，而在各成员预报中，第4、5个减扰预报以及第3个加扰预报都报出了比控制预报好的结果(图略)。从表 1可见，第三簇成功地将第5个减扰预报和第3个加扰预报分离出来。为了分析台风登陆过程，下面只给出了台风登陆前后即预报的第90小时到第240小时三簇850 hPa高度场簇平均随时间演变图(图 3)，其中，图 3a、3b、3c分别为第一、二、三簇的簇平均时间演变图。在簇平均图中，第三簇报出了台风在预报的第132小时登陆，比实况要晚，且在图中台风登陆后没有闭合环流，这可能与模式分辨率及集合预报输出结果时间密度不够有关。第三簇对于台风登陆后向西北方向移动，其后又转向东北方向移动的实况过程没有报出，但实际上第三个加扰预报报出了这一转向的移动路径，簇平均漏报台风转向可能是由于簇成员平均后弱信息被平滑掉的结果。由此可见分簇平均图给出了集合平均预报所不能给出的信息，但一些特殊成员预报也不可忽视。此外特别要注意的是，第三簇所占比重虽然不是最大的，但第三簇包括了集合成员预报较好的成员样本的66.7%，整个簇比重达到30%以上，所以这一簇的预报结果应给予重视。

表 2给出的是以第72小时预报场作为分簇基础，对8月4日起报的10天预报的850 hPa高度场分簇结果。

8月4日08时起报模式，对台风登陆(6日03时)是提前近2天的预报。控制预报和集合平均预报的结果相近，其结果是台风中心都不会到达我国内陆地区。图 4给出了30~120小时三簇850 hPa高度场的簇平均随时间演变图。图 4a、4b、4c分别对应表 2中的第一、二、三簇的簇平均时间演变图。其中只有第一簇报出了台风的登陆及其后的转向移动，但与实况相比，登陆时间推迟了12个小时左右，登陆地点偏北。其余两簇都没有报出台风到达我国内陆，其预报路线为在海面沿西北向移至江淮地区，然后沿海岸线北移到达山东半岛，后两者的差别在于台风中心距离大陆远近。在13个成员预报中第5个加扰预报、第1、2、4、6个减扰预报都成功地预报出了台风登陆以及登陆后先向西北方向移动然后转向东北方向移动的情况。这5个成员中有3个成员包括在第一簇中。

2.1.3 与不采用方差分析的结果对比

如果采用以往常用的96小时预报结果作为分簇基础，8月2日和4日起报的分簇结果见表 3和表 4。

8月2日起报的三簇比重分别为15.4%、61.8%、23.1%，这三簇的簇平均都没有报出台风的登陆。从表中可以看到，预报效果较好的第4个、第5个减扰及第3个加扰的成员预报分别被分在3个簇中。

8月4日起报的三簇的比重为8%、84.6%、8%。只有第一簇报出了台风的登陆及转向，但比起应用方差分析法得到的三簇中第一簇的比重23.7%，可信度小了很多。由此可见，用F检验确定分簇基础是十分必要的，这将大大提高分簇的效果。

2.2 气压场烟羽聚类图

概率烟羽图是为了表示在某一固定地点某个气象要素的集合预报离散度在整个预报期限内的变化情况。具体做法是选取某一关心地点，统计计算集合预报各成员对此点上气象要素的概率分布，然后将所有预报时效的要素概率绘制成等值线图，由于其形状很像烟雾和羽毛，故叫概率烟羽图^[6]。一般而言概率烟羽分布范围较大时，可信度较差；当烟羽出现分叉状态时，大气处于不确定状态^[19]。本文制作的是气压场概率烟羽图，其中气压间隔取1 hPa。

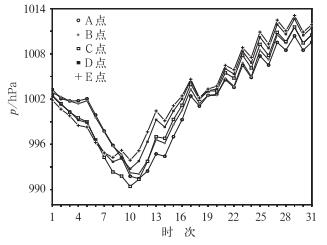
在前面8月4日起报的分簇个例中，第一簇簇平均预报结果是在第54小时(图 4a的第5张小图)台风大致在(30°N、122°E)登陆。由于分簇法仅从大体上提供了几种形势场的可能演变趋势，台风登陆地点的确定还很粗略。为了缩小这一误差，在30°N附近的海岸线上，分别取A(31°N、122.0°E)，B(30°N、120.75°E)，C(29°N、121.75°E)，D(28°N、120.75°E)，E(27°N、120.5°E)五点，通过制作和分析这些点上的气压烟羽聚类图，来进一步确定台风登陆的地点。具体作法是：首先利用双线性插值法将集合预报的海平面气压插值到这5个点，然后将每个点上集合平均预报的海平面气压随时间的演变绘在一张图中(见图 5)。

由于台风是热带地区的暖性低压涡旋，中心的气压值很低，当台风环流靠近某一地区时，该地气压开始缓慢下降，当接近台风中心时，气压出现陡然下降，当达到台风中心时气压达到最低值，台风经过后，气压便迅速回升^[20]。利用台风过境气压的这种变化规律，分析图 5上五点海平面气压的演变，C点的海平面气压随时间下降的幅度最为明显，在8月6日14时达到了气压最低值，由此推测台风有可能在C点登陆，实际上C点与台风实际登陆地点玉环(28.14°N、21.23°E)十分接近，仅偏北不到100 km。气压达到最低值的时间与台风的实际登陆时间8月6日03时相差大约11个小时，产生误差的一种可能原因是模式输出时间密度不够。

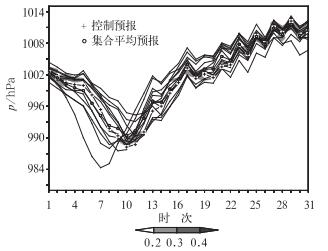
选择C点作海平面气压概率烟羽图(如图 6)用以分析在该点各成员预报的离散度。其中，“+”线代表的是控制预报，“+”线代表的是集合平均预报。阴影区域代表海平面气压的概率。阴影的大值区出现在初始时刻、第18小时(图中对应第4个时次)及第168小时(第25个时次)到216小时(第29个时次)，概率值大于30%，要素预报可信度较高。另外，在第48小时(第9个时次)到第66小时(第12个时次)阴影区对应的概率值也达到了20%以上。在第24小时到第78小时要素分布较分散，出现多分叉现象，即大气处于不确定状态，对这一时段的预报需多加注意。而这正处于台风登陆前后。

为进一步掌握在分叉处海平面气压的离散状况，我们采用系统聚类法中的最短距离法对各成员海平面气压随时间演变趋势进行分类。

系统聚类法是目前国内外常用的一种方法，其基本思想是先将每个样品各自看成一类，n个样品即有n类，选择距离最小的两类并成一个新类，计算新类和其他类的距离，再将距离最近的两类合并，距离计算公式如下^[21-22]：

$ {x_{ijK}} = {x_{iK}}-{x_{jK}} $

(8)

$ {E_{ij}} = \frac{1}{{({m_2}-{m_1} + 1)}}\sum\limits_{K = {m_1}}^{{m_2}} {{x_{ijK}}} $

(9)

其中, i, j代表样本号，取值范围为1~13；K代表离散度大的时次，这里取第5~14个时次，即m₁=5, m₂=14；E_ij代表了i样本对j样本各时次之间的总平均差值。

$ {S_{ij}} = \frac{1}{{({m_2}-{m_1} + 1)}}\sum\limits_{K = {m_1}}^{{m_2}} {\left| {{x_{ijK}}-{E_{ij}}} \right|} $

(10)

S_ij能反映出两个样本中各个时次之间的差值x_ijK对E_ij的离散程度，能较好地反映两样本间的形相似程度。

图 7给出了用系统聚类法对C点海平面气压进行分类的结果，其中图 7a、7b、7c、7d分别代表第一、二、三、四类，粗线条代表类平均，四类中类成员占总集合成员数的百分比分别为38.5%、38.5%、15.4%、7.7%。

通过分析几类图中海平面气压最低点出现的时间，可以预报台风登陆的时间。在图 7中，第一类最低点出现在第60小时(图中对应第11个时次)，第二类最低点出现在第54小时(第10个时次)，第三类最低点出现在第42小时(第8个时次)，第四类最低点出现在第36小时(第7个时次)。尽管第三类所占比重不是最大的，但第三类最低点出现时间最接近实际台风登陆时间，这反映了在业务预报中，这几类情况都不能忽视。

2.3 盒须图(box-whisker plot)

盒须图能提供数据变化范围和极端值的信息。方盒表示中间50%数据的位置，须向盒外两侧延伸至1.5倍半极差范围内最远的数据点^[20]。盒须图具体的制作方法为：从一个四分位数到另一个四分位数画一盒子，并在中位数处画一横线穿过框。然后从框形的每一端画一竖直虚线，竖直虚线止于这样一个区间的极值上，该区间为(下四分位数-1.5×四分位数间距，上四位数+1.5×四分位数间距)^[23]。

盒子中的横线表示的中位数是表明数据位置的一个很好的指标，它在各种情况下都能保持稳定，也就是说中位数是一个稳健估计。使用稳健估计的优势在于，在实际中大多数物理数据组并不是正态分布的，因此样本均值不再是最佳估计量。另一方面，长数据组中不可避免地包含一些远离中心的数据，这时样本均值对于这些数据来说并不具有很好的代表性^[24-25]。对于集合预报来说，难免有一些远离中心的数据，稳健估计可以使要素预报的估计值不受远离中心数据的影响。两个四分位数与中位数的差值可以给出数据偏斜度的某些信息。盒子长度越长，说明数据分布越分散，预报的不确定性越大。除此之外，根据盒子各部分长短的不同，可以判断数据集中的值域。利用两个极值、两个四分位数和一个中位数这样5个数值就能很好地概括集合要素预报^[24]。

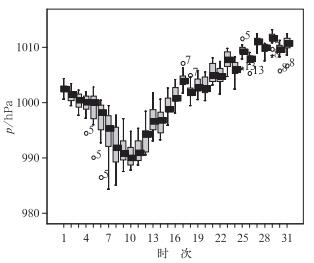
图 8给出了8月4日起报C点海平面气压演变的盒须图，其中小圈代表(下四分位数-1.5×四分位数间距，上四位数+1.5×四分位数间距)区间之外且在(下四分位数-3×四分位数间距，上四位数+3×四分位数间距)区间之内的值，星号代表(下四分位数-3×四分位数间距，上四位数+3×四分位数间距)区间之外的值，图中数字表示成员编号。这样保证在正态分布中有95%的数据均位于盒形图(盒子和两端的须)内。因此，在盒形图外的点能详细地表示集合成员中的一些特殊成员。这样找到的特殊成员的预报结果可能是正确的，也可能误差较大。检验出特殊成员后，不能只作简单的删除。很多情况下，这些成员往往包含比其他成员更多的信息量，必须根据实际情况作仔细分析。

分析图 8可见，在第36小时(图中对应第7个时次)到第48小时(第9个时次)盒子长度及盒子外的须伸展的范围都很大，可由此推测在这一时段预报处于较强的不确定状态，需重点分析，这正对应台风登陆前期。随着盒子长度由长变短再变长，对应了台风的登陆前期、登陆和登陆后的移动。其中5、7、8、13(对应第4、6个减扰预报以及第1、6个加扰预报)这几个成员在显著性检验范围之外, 它们很可能是一些与主体数据相差较远的特殊成员，也可能是单一确定性预报所不能提供的重要信息。盒须图中离散度较大时段内第5个成员(即第4个减扰预报)自第18小时(第4时次)至第30小时(第6个时次)一直在显著性检验之外，由前面分析已知，第4个减扰预报报出了台风的登陆和转向，所以对于这些点也不能忽视。

3 小结

本文利用T106L19全球谱模式和增长模繁殖法，制作了13个成员的中期集合预报，针对“麦莎”台风登陆过程，对集合预报产品进行了解释应用，由于篇幅限制，并没有对影响台风路径的关键天气系统进行预报性能分析，这一内容将另外撰文研究。主要结论如下：

(1) 为提高分簇效果，将方差分析引入离散距离分簇法中，可使分簇基础更加客观和合理，从对850 hPa高度场的集合预报进行分簇的结果看，这种方法可以将不同的预报结果分离出来，特别是对预报效果比较好的成员能分在一簇中，并给出各簇的比重，这与以往采用96小时预报场作为分簇基础的分簇结果相比，效果得到明显改善。

(2) 对台风麦莎的预报，850 hPa高度场可分为三簇，其中一簇的簇平均结果与实况接近。

(3) 根据簇平均图中得到台风可能登陆地点，利用不同点的海平面气压烟羽图，通过分析海平面气压随时间的演变特征，可以进一步订正和确定台风的登陆地点和登陆时间。台风麦莎的试验结果表明，对登陆地点和登陆时间的预报结果都比簇平均图的预报更接近实况。

(4) 对要素烟羽图中多分叉时段利用系统聚类法进行分类，得到预报点海平面气压的烟羽聚类图，反映了几种可能的台风登陆时间。台风麦莎的试验结果被分成四类，同时给出了每一类占集合预报的比重。

(5) 盒须图不仅给出了以往集合预报常用的信息，还给出了数据组主体以外的特殊数据点，这些点可能是大气状态的极端情况，反映了单一确定性预报所不能提供的重要信息，利用这些点可以减少小概率事件的漏报率。