2. 云南省气象台,昆明 650034;
3. 南京信息工程大学电子工程系,南京 210044
2. Yunnan Meteorological Observatory, Kunming 650034;
3. Nanjing University of Information Science & Technology, Nanjing 210044
多普勒天气雷达可以得到目标物沿雷达射线方向的运动速度(即径向速度),有常规测雨雷达不可比拟的优点,但多普勒天气雷达不能测量目标物垂直于雷达射线方向的运动速度(即切向速度),所以发展从单部多普勒雷达所获取的资料中反演风场信息的方法就具有特别重要的实际意义,从多普勒天气雷达测量的径向速度资料中提取风场信息已经提出了不少有实际应用价值的方法,但对散度繁衍方法的研究并不令人满意,特别是多普勒天气雷达所探测到的风场信息存在缺测问题成为了多年一直影响风场信息应用的棘手问题。
20世纪60年代初期,Lhermitt和Atlas[1]提出了单部多普勒天气雷达测量风场的一种方法,称为VAD(Velocity Azimuth Display)技术,应用这种方法,单部多普勒天气雷达可以得到降水区中各高度上的平均风向风速和平均散度等。Srivastava等[2]将VAD方法加以改进推广,称之为推广速度方位显示方法(Extended VAD),简称EVAD方法。然而无论是VAD方法还是EVAD方法,都是在某一固定距离圈上对Vr(θ)作谐波分析的基础上得到的,因此必须考虑Vr(θ)本身的测量误差和距离圈上的局部缺测Vr(θ)(无回波区)资料产生的误差,数值试验证明当无回波区缺口大于30°或者累积缺测区大于60°时,对计算的水平散度有明显的影响,为了减少这种误差,就必须对资料进行处理。最简单常用的方法是插值法,如胡明宝等[3]采用拉格朗日插值公式补缺测点,梁海河等[4]提出了k-邻域频数法来消除风场中的“噪声”和填补缺测,王凌震等[5]探讨了一种遮挡范围内进行数据插补的技术方法,以弥补雷达产品生成中的缺陷问题,尤其是解决雷达定量测量面降雨量场的补缺问题,但此方法只是很简单地用较高仰角的资料对相应的低仰角无回波区进行填补,万蓉等、汤达章等、忻翎艳等[6-9]提出了对原始的多普勒速度资料进行中值滤波处理,但在某距离圈上连续的方位缺测区大于30°或者总方位缺测值大于60°时,误差偏大。就目前来说,由于挡角造成无回波区和降水回波区实测无回波区中的多普勒速度资料填补技术,目前国内外均无有效的方法。本文在线性风场的条件下,利用迭代法对模拟的多普勒速度场无回波区进行填补,分析迭代法填补的精度和适用范围。数值模拟的试验表明,迭代法填补速度场无回波区能极大的改善从多普勒速度场中提取平均散度和平均形变信息的精度。
1 迭代法原理介绍在线性风场条件下,假定雷达低仰角扫描某一距离圈存在无回波区,定义该距离圈上Vr随方位角的分布为Vr0(θ)[Vr0(θ)包括有回波区部分Vr0(θ)′和无回波区部分Vr0(θ)″],具体方法如下:
① 由VAD理论[3]
| $ \begin{array}{l} {V_r}(\theta ) = {u_0}\cos \theta \cos \alpha + {v_0}\sin \theta \cos \alpha + \frac{1}{2}({u_x} + {v_y}) \times \\ \;\;\;\;\;\;\;\;\;\;\;r\cos \alpha + \frac{1}{2}({u_x}-{v_y})r\cos 2\theta \cos \alpha + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}({u_y} + {v_x})r\sin 2\theta \cos \alpha-{V_f}\sin \alpha \end{array} $ | (1) |
式(1) 中的θ和α分别是方位角和仰角,r为等距离圈的半径。当雷达低仰角扫描时,由于垂直速度对Vf多普勒速度Vr(θ)贡献很小,可以忽略不计。因此对式(1) 作谐波分析可得
| $ \left\{ \begin{array}{l} {u_x} + {v_y} = \frac{2}{{Mr\cos \alpha }}\sum\limits_{i = 1}^M {{V_{ri}}} \\ {u_0} = \frac{2}{{M\cos \alpha }}\sum\limits_{i = 1}^M {{V_{ri}}} \cos {\theta _i}\\ {v_0} = \frac{2}{{M\cos \alpha }}\sum\limits_{i = 1}^M {{V_{ri}}} \sin {\theta _i}\\ {u_x}-{v_y} = \frac{4}{{Mr\cos \alpha }}\sum\limits_{i = 1}^M {{V_{ri}}} \cos 2{\theta _i}\\ {u_y} + {v_x} = \frac{4}{{Mr\cos \alpha }}\sum\limits_{i = 1}^M {{V_{ri}}} \sin 2{\theta _i} \end{array} \right. $ | (2) |
将Vr(θ)代入式(1) 和式(2),可以得到一组平均风向风速、散度项和形变项,即u0, v0, ux+vy, ux-vy, uy+vx,也称为0、1、2阶谐波分量。
② 将步骤① 中所求得的u0, v0, ux+vy, ux-vy, uy+vx代入公式(1) 得到一组新的Vr随方位角的分布,定义其为Vri(θ)。[Vri(θ)中对应于Vr0(θ)中有回波的部分称为Vri(θ)′,对应于Vr0(θ)中无回波的部分称为Vri(θ)″]。
③ 由于距离圈存在无回波区,因此步骤①、② 中计算u0, v0, ux+vy, ux-vy, uy+vx时的结果是有误差的,无回波区越大,误差越大,为了减小误差,用Vri(θ)″对Vr0(θ)进行填补。具体做法是:保留Vr0(θ)中有回波的点,无回波的部分Vr0(θ)″用Vri(θ)″替代,最后得到一组新的Vr(θ)随方位角的分布,定义其为Vr2(θ)。
④ 经过上面的处理之后,相对于理想的径向速度资料还是有误差的,对该距离圈计算一个速度均方根误差RMS
| $ RMS = \sqrt {\frac{1}{M}\sum\limits_{i = 1}^M {{{[{V_{ri}}(\theta ) - {V_{ri}}(\theta )']}^2}} } $ | (3) |
M为Vr0(θ)中有速度值点的总数。RMS值越小表明迭代过后所得的径向速度资料相对于原始的资料的误差越小。
⑤ 为了能使误差降低到最小,利用步骤③ 所求得的新的Vr(θ)随方位角的分布Vr2(θ)。重复上述①、②、③、④ 步骤,计算得到一系列的RMS,当RMS达到最小时,步骤③ 通过迭代得到的Vr2(θ)即是所要得到的径向速度场。
这里提出的方法是根据VAD理论,考虑0、1、2阶谐波项(区别于最小二乘法),利用迭代法对无回波区不断填补,不断缩小误差到最小而实现,能有效解决正负速度区缺测问题。
2 回波信号模拟的基本理论由于实测多普勒雷达的线性风场是存在噪声干扰的,为了更好地验证迭代法填补多普勒速度场无回波区的可行性,需要对模拟的回波信号进行加噪处理,使模拟的附加了一定噪声的回波信号在性质上与实测雷达的降水回波信号保持一致,即模拟的降水回波信号在时域和频域要与实际情况相符。具体做法是:首先对模拟信号进行采样,然后附加一定信噪比的白噪声,得到降水回波的离散功率谱密度函数,再通过反傅立叶变换法将降水回波的功率谱密度函数转变为回波的时域信号。由于在迭代法和VAD填补试验中只需要模拟的多普勒速度场,因此本文利用脉冲对处理法(PPP法)对时变函数进行处理,最后得到多普勒速度谱的零阶距(回波功率)、1阶距(平均多普勒速度)和2阶距(多普勒速度谱宽)。
2.1 模拟信号的采样及加噪处理相对于大多数降水回波信号,功率谱密度函数为
| $ Gn = \frac{1}{{{\sigma _f}{{(2\pi )}^{\frac{1}{2}}}}}\exp [-\frac{{{{({f_n}-\overline f )}^2}}}{{2{\sigma _f}^2}}] $ | (4) |
Gn是与fn相对应的离散的谱密度函数,f是功率加权的中间频率,即多普勒频率,f总是正的且小于fN(Nyquist频率)并且存在这样的不等式-fN < fn < fN[3]。
降水回波的功率谱密度通常呈高斯谱分布,而谱分析的信号是离散的谱信号, 必须对原谱进行离散化[10-11],用采样公式可得到离散谱函数Sn。为使模拟信号尽可能符合实际情况,需对模拟的谱函数附加一定信噪比的白噪声,用加噪公式可得到加噪后的离散功率函数PN。加噪后模拟信号的离散功率谱密度函数为
| $ {S_n} =- \ln ({x_n})[KGn + \frac{{{P_N}}}{N}] $ | (5) |
式中0 < xn < 1,是一个在(0,1) 之间呈均匀分布的随机数,K是信噪系数,
| $ K = \frac{{{P_N}{{10}^{SNR/10}}}}{{\sum\limits_n {Gn} }} $ | (6) |
PN是噪声功率,
|
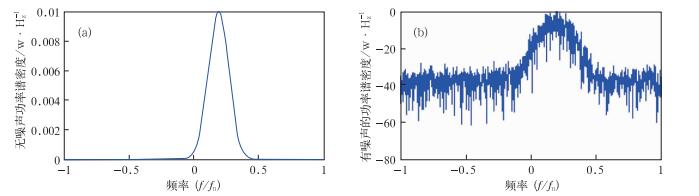
图 1 径向速度为Vr=5 m·s-1(对应的多普勒频率为fd=100 Hz)无噪声和附加20 dB信噪比(SNR=20 dB)白噪声后的离散功率谱密度图 (a)无噪声;(b)附加SNR=20 dB白噪声 Fig. 1 The discrete power spectral density chart of non-noise and white noise of 20 signal-to-noise ratios (SNR=20 dB) when the radial velocity Vr=5 m·s-1 (corresponding to Doppler frequency of 100 Hz) (a) non-noise, (b) white noise of 20 dB |
对式(4)、式(5) 中所求得的实谱序列附加上相位谱,考虑到噪声的随机性,附加0~2π概率分布均匀的随机相位谱分布,得到复谱序列[10],即由
| $ {A_n} = S_n^{\frac{1}{2}}\cos (2\pi {y_n}) $ | (7) |
| $ {B_n} = S_n^{\frac{1}{2}}\sin (2{\rm{\pi }}{y_n}) $ | (8) |
yn是(0,1) 区间上概率均匀分布的随机数,随后通过傅里叶反变换[3]得到时域信号。
2.3 利用脉冲对处理法(PPP法)得到加噪的径向速度由于本文在进行数值模拟时仅需要多普勒速度谱的0阶距(回波功率)、1阶距(平均多普勒速度)和2阶距(多普勒速度谱宽),而不需要知道整个谱的详细结构,因此利用脉冲对处理法(PPP法)对采样信号进行处理。PPP法的特点是在假定雷达照射体积内每一个粒子的径向速度脉动具有偶函数的分布密度条件下,可以不对信号进行谱分析,而是采用相继的二个取样值成对的进行处理,直接得到平均多普勒频率和速度。
设Zn和Zn+1是{Zn}回波信号序列中相继取样的两个信号值[3],两个信号之间的时间间隔为Ts,且一系列的回波信号的总数N,则根据自相关函数的定义[12]有:
| $ R({T_s}) = \frac{1}{N}\sum\limits_{j = 0}^{N-1} {{Z_{j + 1}}{Z_j}} $ | (9) |
信号的复数形式为
Z(t)=X(t)+jY(t),
且有
X(t)=acosϕ(t), Y(t)=asinϕ(t)
于是式(9) 就可写成
| $ \begin{array}{l} R({T_s}) = \frac{1}{N}\sum\limits_{j = 0}^{N-1} {{Z_{j + 1}}{Z_j}} = \frac{1}{N}\sum\limits_{j = 0}^{N-1} {{Q_{n + 1}}{Q_n} + } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{I_{n + 1}}{I_n} + j({Q_{n + 1}}{Q_n}-{I_{n + 1}}{I_n}) \end{array} $ | (10) |
结合式(7)、式(8),则加噪后的径向速度为:
| $ {V_r} = \frac{\lambda }{2}\overline {{f_0}} = \frac{\lambda }{{4\pi {T_s}}}\arctan \left\{ {\frac{{{\rm{Im}}\left[ {R({T_s})} \right]}}{{{\rm{Re}}\left[ {R({T_s})} \right]}}} \right\} $ |
Re[R(Ts)]、Im[R(Ts)]分别为复数的实部和虚部。
模拟风场的每一个径向速度所对应的多普勒频率
为验证迭代法填补径向速度场无回波区的精度,本文进行数值模拟试验。首先考虑VAD算法中径向速度展开的傅氏级数中包含0、1、2阶谐波,模拟平面线性风场的特征参数如表 1所示,根据公式(1),再由表 1的特征参量得到全方位上二维径向速度模拟场,模拟中用到的假设为:雷达探测距离150 km;雷达仰角0.5°;脉冲重复频率PRF为1024 Hz;雷达发射的波长10 cm;信噪比的取值范围0~40 dB;PPP法中取32个脉冲对;方位角采样间隔为1°;每条径向上每隔150 m模拟一个径向速度资料库,共模拟1000条等距离圈的径向速度资料库。
|
|
表 1 模拟含0、1、2阶谐波的线性风场特征参量(单位:m·s-1) Table 1 The characteristic parameters of simulated linear wind field containing 0, 1, 2 step overtones |
本文设计的线性风场是通过在某一固定距离圈上对Vr(θ)作谐波分析的基础上得到的,所以此模拟风场上的每一个径向速度都在VAD显示的速度方位曲线上,此径向速度不含有雷达的机内噪声,为了使模拟风场更加接近实际风场,对上述模拟风场的每一个径向速度附加不同信噪比和不同速度谱宽的噪声,模拟得到带噪声的径向速度场,模拟过程中存在速度模糊的地方均做了退模糊预处理。
在模拟得到Vr(θ)的基础上,人为设定无回波区,利用前面介绍的迭代法对缺口进行填补,得到填补后的径向速度场资料,通过比较不同缺口在不同噪声情况下迭代填补的平均RMS值、平均迭代次数、0、1、2阶谐波分量相对误差ε的平均值(其中
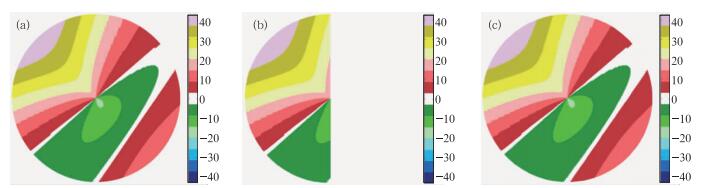
首先检验模拟的多普勒径向速度场在无噪声情况下,用迭代法填补的精度。本文选取随机连续性缺口累积值为10°, 20°, 30°, …, 180°,用迭代法填补结果见表 2,可见在模拟的一个平面线性速度场无噪声情况下,随着连续累积缺口的不断增大,终止迭代的次数不断增多,终止迭代时RMS平均值、0、1、2阶谐波的平均相对误差值也逐渐增大但增长幅度较小,所有相对误差值均接近0,说明迭代填补后平面径向速度场的0、1、2阶谐波分量几乎不变,从而验证了迭代法填补多普勒速度场无回波区在无噪声情况下的精确性。从表 2还可看出,80 km距离圈上缺口处迭代前后速度相对误差值均为0,说明填补前后速度场均能保持原有的特征。从连续缺口180°的迭代前后填补效果图看出(图 2),即使是在较大缺口的情况下,迭代法填补前后缺口处的径向速度场仍然没有任何改变。显然,迭代法能非常精确地填补无噪声情况下缺口值在180°以内的速度场。
|
|
表 2 迭代法填补平面无噪声速度场无回波区结果 Table 2 The result of filling non-echo area of plane non-noise velocity field with repetitive processing |
|
图 2 无噪声连续累积缺口180°平面线性速度场迭代填补前后图 (a)模拟图;(b) 180°缺口图;(c)迭代填补图 Fig. 2 The comparison images of the simulated and non-noise velocity field that filled continuously gap 180° iteration non-echo areas with repetitive processing (a) simulation image, (b) the 180° gap image, (c) filled image |
模拟回波信号由平均多普勒频率、速度谱宽σv(或频率谱宽σf)、信噪比SNR这3个参数决定,故速度谱宽、信噪比SNR的变化将引起径向速度以及用VAD方法得到的水平散度的变化。为进一步验证迭代法填补速度场无回波区的精度,取SNR值分别为0、5、15、20、30、40和σv值分别为1、2、3、4、5、6来填补速度场无回波区,并验证填补的精度和效果。
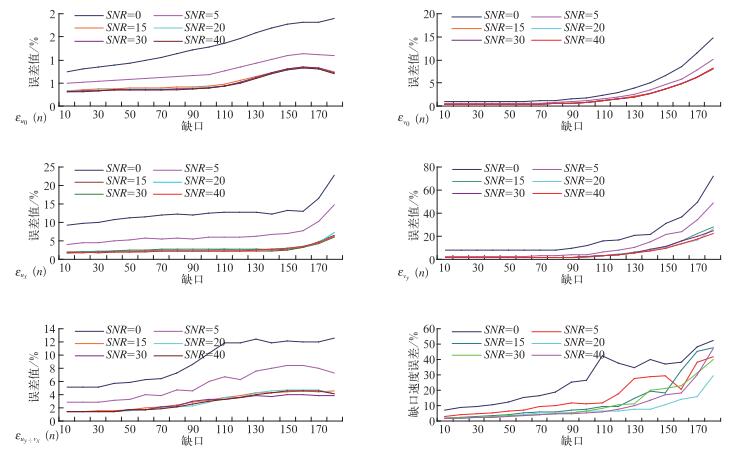
3.3.1 速度谱宽σv一定(σv=2 m·s-1),信噪比SNR变化分别对模拟的带有SNR分别为0、5、15、20、30、40噪声的平面径向速度场进行连续性缺口10°~180°的迭代填补,结果见图 3和表 3,在信噪比不变的情况下,随着累积缺测区的增大,迭代次数也逐渐增多,终止迭代时平均RMS值也呈线性增大但增长幅度较小,迭代法填补径向速度场缺测区所得的u0, v0, ux+vy, ux-vy, uy+vx的相对误差εu0、εv0、εux、εvy、εuy÷vx都相应的增大;一个距离圈上迭代填补前后速度值相对误差ε也呈线性增长趋势,ε值在180°累积缺口时最大可达52.56%;当SNR不同时,在累积缺口≤120°条件下,随着SNR的减小,εu0、εv0、εux、εvy、εuy÷vx、80 km距离圈上ε值基本呈缓慢线εv0性增加趋势,0、1、2阶谐波的总体误差能控制在15%以内,缺口处速度场迭代填补前后的ε值也基本能控制在30%左右;当累积缺口≥120°时,εv0、εux、εvy呈显著性线性增加趋势,εu0、εuy÷vx呈先增大、后减小的变化趋势,80 km距离圈上ε呈现先增大,后减小,再增大的变化趋势,这可能是由于随着累积缺口增加,噪声功率对迭代填补求取平均ε的影响也逐渐减小的缘故,说明迭代法填补在累积缺口≥120°时效果不好;当SNR≤5时,由于噪声功率较大,εu0、εv0、εux、εvy、εuy÷vx和80 km距离圈上ε值增加很快,迭代法填补速度场无回波区的效果不明显,说明迭代法填补多普勒速度场无回波区受信噪比SNR和累积缺口的影响较大,在SNR≥5、累积缺口≤120°时迭代填补的误差能满足实际业务需求。
|
图 3 不同SNR条件下,迭代法填补径向速度场无回波区误差分析图 Fig. 3 Under different SNR conditions, the error analysis of filling velocity field non-echo area with repetitive processing |
|
|
表 3 不同SNR条件下迭代法填补10°~180°缺测区域的平均值 Table 3 Under different SNR conditions, the average RMS analysis result of filling continuously gap from 10° to 180° iteration radial velocity field non-echo area with repetitive processing |
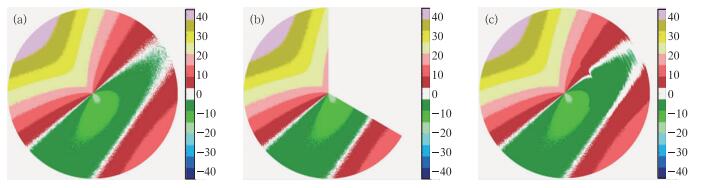
以SNR=15 dB、σv=2 m·s-1随机取连续性累积缺口为120°为例(图 4),图 4a为模拟的带SNR=15、σv=2 m·s-1噪声的平面径向速度场图,图 4b为人为设计的120°连续性缺口,图 4c为迭代填补后的速度图,可以看到填补效果较好。因此本文建议的迭代法在信噪比SNR≥5、连续累积缺口≤120°的情况下,能较高精度地填补平面径向速度场无回波区。
|
图 4 SNR=15 dB、σv=2 m·s-1连续累积缺口120°时迭代填补前后平面速度图 (a)模拟图; (b)缺口图; (c)填补图 Fig. 4 When SNR=15 dB, σv=2 m·s-1, the comparison images of the simulated velocity field that filled continuously gap non-echo areas with repetitive processing (a) simulation image, (b) the 120° gap image, (c) filled image |
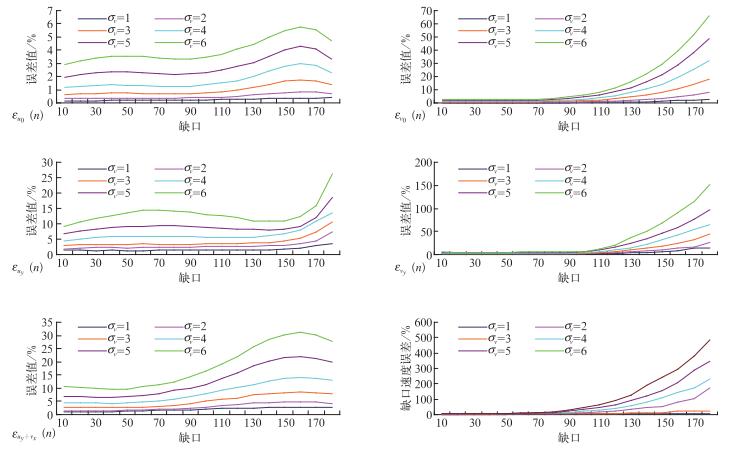
在SNR=20 dB、σv=1, 2, 3, 4, 5, 6 m·s-1条件下,模拟的6个带噪声的平面径向速度场,分别进行连续性缺口10°~180°迭代填补,结果如表 4和图 5所示,在谱宽一定的条件下,随着累积缺测区的增大,迭代次数也逐渐增多,终止迭代时平均RMS值也呈线性增大但增长幅度较小,迭代法填补径向速度场缺测区所得的u0, v0, ux+vy, ux-vy, uy+vx的相对误差εu0、εv0、εux、εvy、εuy÷vx都相应的增大;一个距离圈上迭代填补前后速度值相对误差ε也呈线性增长趋势;当σv不同时,随着σv的增大εu0、εv0、εux、εvy、εuy÷vx及80km距离圈上迭代法填补缺测区的速度值相对误差ε增大非常明显,尤其在缺测区>120°时,0、1、2阶谐波相对误差基本上都在15%以上,ε值则达到了100%以上,迭代填补效果并不明显;当σv < 3 m·s-1、缺测区域 < 120°时,0、1、2阶谐波相对误差均在10%以内变化,80 km距离圈迭代法填补缺测区速度值相对误差ε在1%到20%之间变动,说明在此缺测区范围迭代法填补精度较高,效果较好;σv>4 m·s-1时,缺测区域>120°以上的迭代法填补效果并不理想,0、1、2阶谐波相对误差均大于10%,80 km距离圈的速度ε值均大于30%,特别是σv=6 m·s-1时,100°缺测区的εuy÷vx值已达到19%、80 km距离圈的速度ε已达到30.5%,填补效果不好。由此可见,速度谱宽的大小对迭代法填补平面速度场无回波区有较大影响,本文建议,在用迭代法填补速度场缺测区域时,累积连续缺口最好在120°以内,速度谱宽σv最好在4 m·s-1以下填补效果和精度才能达到满意效果。
|
|
表 4 不同σv条件下迭代法填补10°~180°缺测区域的平均值 Table 4 Under different σv conditions, the average RMS analysis result of filling continuously gap from 10° to 180°iteration radial velocity field non-echo area with repetitive processing |
|
图 5 不同σv条件下,迭代法填补径向速度场无回波区误差分析图 Fig. 5 Under different σv conditions, the error analysis chart of filling radial velocity field non-echo area with repetitive processing |
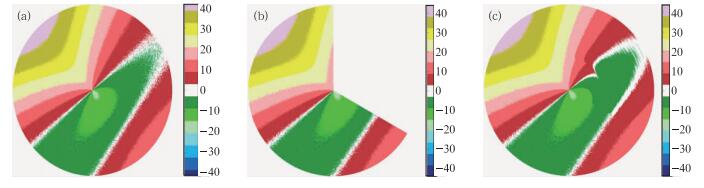
以SNR=20 dB、σv=3 m·s-1随机取连续性累积缺口为120°为例(图 6),图 6a为模拟的带SNR=20、σv=3 m·s-1噪声的平面径向速度场图,图 6b为人为设计的120°连续性缺口,图 6c为迭代填补后的速度图,可以看到填补效果较好。因此本文建议的迭代法在信噪比σv≤3 m·s-1、连续累积缺口≤120°的情况下,能较高精度地填补平面径向速度场无回波区。
|
图 6 SNR=20 dB、σv=3 m·s-1连续累积缺口120°时迭代填补前后平面速度图 (a)模拟图; (b)缺口图; (c)填补图 Fig. 6 When SNR=20 dB、σv=3 m·s-1, the comparison images of the simulated radar velocity field that filled continuously gap 120° iteration non-echo areas with repetitive processing (a) simulated image, (b) the 120°gap image, (c) filled image |
在实际情况下,测站周围的降水回波分布不均匀,同一距离圈上存在着不同的缺测数;另外在资料使用前必须做质量检验、剔除奇异点,这样也会出现一些空隙和缺测区域。为此,模拟了随机取的非连续性缺口(代表积累的Vr(θ)缺测区)即非全方位不均匀采样,从而使模拟回波的速度资料更加接近真实情况。
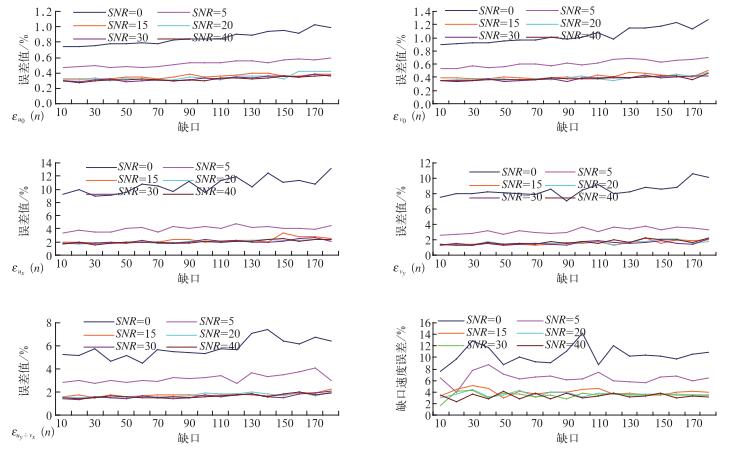
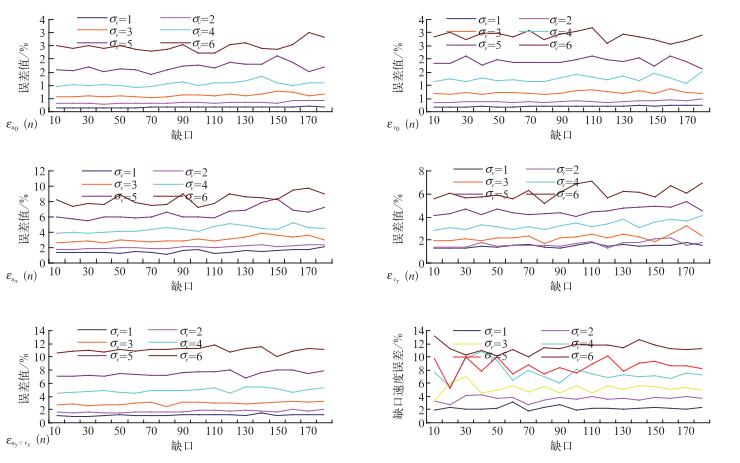
本文分别对模拟的带有σv=2 m·s-1, SNR=40、30、20、15、5、0 dB和SNR=20 dB,σv=6, 5, 4, 3, 2, 1 m·s-1噪声的12个平面线性速度场随机取非连续性缺口0°~180°,并用迭代法进行无回波区填补,结果如图 7、图 8所示,在同一个噪声情况下,随着累积缺测区的增大,迭代次数也逐渐增大但增大幅度很小,0、1、2阶谐波相对误差和80 km距离圈上迭代法填补缺测区的速度值相对误差ε增幅几乎不变,说明对于非连续性缺口的平面速度场,缺口的大小对迭代次数和迭代效果的影响较小,迭代法填补的精度和效果能达到满意程度;在速度谱宽σv固定SNR改变的条件下,随着SNR减小即机内噪声逐渐增大,0、1、2阶谐波相对误差和80 km距离圈上迭代法填补缺测区的速度值相对误差ε有缓慢增加趋势但误差值均控制在15%以内,对SNR固定速度谱宽σv改变的条件下,随着σv的逐渐增大,误差值的变化趋势与上述基本一致,总体误差也都控制在15%以内,说明对模拟的附加不同噪声的平面径向速度场,用迭代法填补随机非连续性缺口时,噪声和缺口大小对迭代填补的效果影响较小,迭代法能较为精确地填补非连续缺口在180°以内的附加不同噪声的平面径向速度场。
|
图 7 不同SNR条件下,迭代法填补随机缺口径向速度场无回波区误差分析图 Fig. 7 Under different SNR conditions, the error analysis chart of the random gap velocity field non-echo area filled with repetitive processing |
|
图 8 不同σv条件下,迭代法填补随机缺口径向速度场无回波区误差分析图 Fig. 8 Under different σv conditions, the error analysis chart of the random gap velocity field non-echo area filled with repetitive processing |
在数值模拟的基础上,本文利用迭代法对实测多普勒速度场无回波区进行填补。云南的6部CINRAD-CC多普勒天气雷达在实际探测风场资料中常出现因地物阻挡造成缺测和实际观测两种无回波区。本文选取速度场资料比较完整的普洱雷达、存在实际无回波区的昆明雷达和因挡角造成无回波区的丽江雷达的探测资料,进行有代表性的迭代填补实验。
3.5.1 实测多普勒雷达完整速度场人为缺口的无回波区迭代填补效果分析选取2007年7月19日10:48速度场资料比较完整的普洱多普勒速度场探测资料(0.5°仰角),人为做0°~110°的连续缺口,然后用迭代法对无回波区进行填补。从填补效果分析(图 9),填补后的速度图不但能消除奇异点的影响,还能较好反映缺测的零速度线的走向,同时还能更清晰地反映出大范围辐合线性分场特征。
|
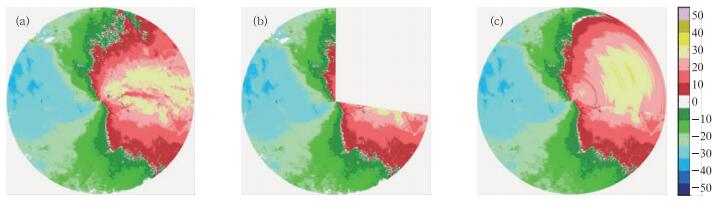
图 9 普洱实测速度图连续累积缺测方位角110°填补效果 (a)原始图像; (b)连续累积110°缺口图; (c)填补图 Fig. 9 The comparison images of the actual observed radar velocity field that filled continuously gap 110° iteration non-echo areas with repetitive processing in Pu'er radar station (a) original image, (b) the 110° gap image, (c) filled image |
选取2007年7月19日15:22本身存在非连续无回波区较多的昆明雷达速度场资料(0.5°仰角)和2007年7月20日7:22因地物阻挡造成的低仰角回波缺测区域较多的丽江多普勒速度场探测资料(1.5°仰角),利用迭代法对无回波区进行填补。从填补前后图像(图 10)对比分析可看出,对昆明实测速度场资料,填补后的速度图能基本消除奇异点的影响,迭代填补后的图像与原图几乎保持一致的零速度线特征。迭代填补后风场的分布特征更加明显,使填补后图像更适合于定量降水估算和风场散度与形变等信息的提取。对丽江实测多普勒速度场资料,当一个等距离圈上的累积缺口≤120°时,迭代法填补效果比较满意,填补后的速度场能较清晰地显示出风场的零速度线走向、速度场中心区位置和风场辐合等特征。

|
图 10 昆明、丽江雷达站实测多普勒速度场资料迭代填补前后图 (a)昆明实测速度图;(b)昆明填补图;(c)丽江实测速度图;(d)丽江填补图 Fig. 10 The comparison images of the actual observed Doppler velocity field that filled non-echo areas with repetitive processing in Kunming and Lijiang radar stations (a) Original velocity image in Kunming, (b) filled velocity image in Kunming, (c) Original velocity image in Lijiang, (d) filled velocity image in Lijiang |
通过理论分析和对模拟资料的计算分析以及实测多普勒速度场无回波区填补,结果表明:
(1) 对模拟的无噪声平面径向速度场,迭代法能基本无误差的填补连续累积缺口值在180°以内的速度场,填补后0、1、2阶谐波误差绝对值及80 km距离圈上迭代填补缺测区速度误差均趋向0。
(2) 对模拟的连续性累积缺口为0°~180°的平面径向速度场,在σv=2 m·s-1, SNR=40、30、20、15、5、0 dB的情况下,迭代法填补速度场无回波区在SNR≥5 dB、连续累积缺口≤120°条件下填补精度和效果较好,填补后0、1、2阶谐波误差绝对值均控制在15%以内,80 km距离圈上迭代填补缺测区的速度误差控制在30%以内。
(3) 对模拟的连续性累积缺口为0°~180°的平面径向速度场,在SNR=20 dB,σv=1, 2, 3, 4, 5, 6 m·s-1情况下,迭代法填补速度场无回波区在σv≤4 m·s-1,连续累积缺口≤120°条件下填补精度和效果较好,填补后0、1、2阶谐波误差绝对值均控制在15%以内,80 km距离圈上迭代填补缺测区的速度误差控制在30%以内。
(4) 对模拟的非连续性累积缺口为0°~180°的平面径向速度场,在不同速度谱宽和不同SNR条件下,迭代法均能较为精确地填补速度场无回波区,填补后0、1、2阶谐波误差绝对值及80 km距离圈上迭代填补缺测区的速度误差均能控制在15%以内。
(5) 用迭代法对实测多普勒速度场进行填补,发现对人为缺口的无回波区和存在因挡角和本身无回波区的速度场资料,在连续累积缺口≤120°情况下,迭代法均能较好地填补无回波区,填补效果较好,填补后的速度图不但能消除奇异点的影响,较好反映缺测的零速度线的走向,还能更清晰地反映出大范围辐合线性分场特征,使填补后图像更适合于计算机反演降水定量算法、风场散度、形变等信息的提取。
Lhermitte R H, Atlas D. Receptation motion by pulse Doppler radar [A], Preprint 9th conference on Radar Meterology [C]. Boston: Amer Meteor Soc, 1961:218-223.
|
Thomas Matejks, Srivastava, 1991. An improved version of the extended velocity-azimuth display analysis of single-Doppler data[J]. J Atmos Oceanic Technol, 8(4): 453-456. DOI:10.1175/1520-0426(1991)008<0453:AIVOTE>2.0.CO;2 |
胡明宝, 高太长, 汤达章, 2000. 多普勒天气雷达资料分析与应用[M]. 北京: 解放军出版社.
|
梁海河, 张沛源, 葛润生, 2002. 多普勒天气雷达风场退模糊方法的研究[J]. 应用气象学报, 13(5): 591-599. |
王凌震, 王啸华, 薛小宁, 等, 2005. 新一代天气雷达观测受遮挡范围内数据插补补技术方法[J]. 气象科学, 25(4): 405-409. |
万蓉, 汤达章, 张鹏, 等, 2003. 非线性风场的VAD分析初探[J]. 气象科学, 23(3): 314-323. |
忻翎艳, 汤达章, 1990. 由VVP探测技术提取风场信息的方法[J]. 气象科学, 10(4): 400-408. |
汤达章, 忻翎艳, 1989. VAD和VARD速度资料获取风场信息的方法[J]. 南京气象学院学报, 12(3): 66-73. |
徐芬, 夏文梅, 吴蕾, 等, 2007. 多普勒天气雷达速度PPI图散度分布信息提取[J]. 气象, 33(11): 21-27. DOI:10.7519/j.issn.1000-0526.2007.11.004 |
Dale Sirmans, Bill Bungarner, 1975. Numerical Comparison of Five Mean Frequency Estimators[J]. Appl Meter, 14(9): 991-1003. |
杜晓勇, 张鹏, 胡明宝, 2002. VAD技术反演平均风向风速的研究[J]. 解放军理工大学学报, 3(3): 81-84. |
赵恒轩, 1999. 天气雷达及其信号处理[M]. 乌鲁木齐: 新疆大学出版社.
|
 2010, Vol. 36
2010, Vol. 36 