2. 中国气象科学研究院,北京 100081
2. Chinese Academy of Meteorological Sciences, Beijing 100081
空气温度是表示热量特征的重要指标之一,是进行热量资源分析、自然区划、农业生产潜力估算的重要参数[1-2]。空气温度也是地球大气系统能量和水分循环的关键参数,在陆地过程模式、气候和数值天气预报区域或全球模式中扮演着越来越重要的角色。气象数据都是单点观测的,气象观测台站数量有限而且分布不均匀,空间代表性较差,在区域尺度模型中应用还存在一些问题。因此许多空间插值方法如反距离加权插值法、最近邻点插值法、多元回归法、三角网线性插值法、三次B样条法、克里格法等在气象学领域得到广泛的应用。然而不同插值方法的优化权重标准是不一样的,如果观测点足够多,大多数插值技术得到的结果基本相似,如果观测站点比较稀疏,不同的插值方法得到的结果差别比较大。遥感技术的发展为获取区域尺度的地表参数提供了一个重要手段。目前不少学者对陆地表面温度遥感反演方法进行了大量的研究,反演误差基本在1℃之内[3-5],但从遥感探测数据中直接提取空气温度在精度上还很难满足气象业务应用需求。
当前从卫星遥感观测数据估算空气温度方法的研究比较多。一是直接从卫星遥感反演的地表温度(Land Surface Temperature, TLS)和气温的统计关系来推算。如Chen等[6]研究发现利用GOES静止气象卫星的热红外数据推算的空气温度与实际1.5 m观测空气温度的线性回归系数R2=0.76,回归方程的标准差为1.3~2.0 ℃。Horiguchi等[7]也利用1.5 m高度气象台站观测的实际空气温度与静止气象卫星反演的地表温度进行回归分析,发现估算的空气温度误差在1~1.7 K。最近,Green等[8]发现在非洲和欧洲大陆,从AVHRR反演的TLS与气象台站观测的月平均温度有着连续显著的相关性。
另一种方法主要是基于NDVI和TLS的梯形或三角形的空间特征关系。由于植被的数量在空间分布上是趋于不均匀的,观测的TLS将随植被的变化而变化[9]。Saravanapavan等[10]研究认为TLS随着NDVI的增加而降低,空气温度可以通过全覆盖植被的NDVI值外插来估算。在浓密植被覆盖条件下,植被的冠层温度几乎接近其周围空气温度。因此基于TLS和NDVI空间特征关系的空气温度估算方法被提出来,即“Vi-Ts”(Vegetation Index-Surface Temperature)方法[11-13]。该方法对于中、高植被覆盖区域比较适用,但对于稀疏植被地区,误差很大。
笔者在前人的研究基础上,分别建立了稀疏植被(NDVI≤0.25) 和中、高覆盖植被(NDVI>0.25)[14]地区的空气温度遥感反演方法。
1 数据与方法 1.1 地表温度反演原理与方法目前从卫星遥感反演地表温度的主要方法有单一红外通道法、分裂窗法、日夜法等[3]。本文采用常用的分裂窗算法,其基本原理如下,
由于在10.5~12.5 μm波长之间,太阳辐射非常弱,利用卫星传感器获得辐射亮度值R(μ)可以利用辐射传输公式描述[15-16],
| $\begin{array}{l} R\left( {{v_i},\mu } \right) = B\left( {{v_i},{T_s}} \right){\rm{ \mathsf{ ε} }}\left( {{v_i},\mu } \right)\tau \left( {{v_i},\mu ,{p_s}} \right) + \\ \quad \quad \quad {R_a}\left( {{v_i},\mu } \right) + \int\limits_0^{2\pi } {\int\limits_0^1 {\mu '{f_r}} } \left( {{v_i}, - \mu ',\phi '} \right) \times \\ \quad \quad \;{R_d}\left( {{v_i}, - \mu ',\phi '} \right)\tau \left( {{v_i}, - \mu ',\phi ',{p_s}} \right){\rm{d}}\mu '{\rm{d}}\phi ' \end{array}$ | (1) |
式中R(vi, μ)是波段辐射的平均测量值,vi为波数,μ是当地观测天顶角的余弦,B(vi, Ts)是地表温度为Ts的普朗克函数,ε(vi, μ)是地表有效比辐射率,τ(vi, μ, ps)是沿θ观测角从大气压为ps的地表到大气顶层的大气整层透过率。上式右边第一项是地表辐射经大气削弱到达传感器的部分,第二项是大气上行辐射,第三项大气下行辐射经地表反射并穿过大气达到传感器的部分。
在分裂窗反演地表面温度的算法中,主要的参数有地表温度Ts、大气状况、分裂窗两个波段的观测辐射亮度值和两个波段的地表发射率值。利用AVHRR的第4和第5通道的观测值T4和T5以及两个通道的发射率ε4和ε5,可以得到地表温度的解析公式:
| $\begin{array}{l} {T_s} = \left( {{A_1} + {A_2}\frac{{1 - \varepsilon }}{\varepsilon } + {A_3}\frac{{\Delta \varepsilon }}{{{\varepsilon ^2}}}} \right)\frac{{{T_4} + {T_5}}}{2} + \\ \quad \quad \left( {{B_1} + {B_2}\frac{{1 - \varepsilon }}{\varepsilon } + {B_3}\frac{{\Delta \varepsilon }}{{{\varepsilon ^2}}}} \right) \times \left( {{T_4} + {T_5}} \right) + C \end{array}$ | (2) |
ε为AVHRR第4、5通道地表发射率的平均值,Δ ε为AVHRR第4、5通道地表发射率之差。A1、A2、A3和B1、B2、B3、C为方程系数。许多学者基于各自简化的辐射传输方程提出了许多修正的分裂窗算法,其中Ulivieri等[17]提出的分裂窗算法最具代表性:
| ${T_s} = {T_4} + 1.8\left( {{T_4} - {T_5}} \right) + 48\left( {1 - \varepsilon } \right) - 75\Delta \varepsilon $ | (3) |
式中,T4、T5分别为AVHRR第4、5通道亮温(K);ε4和Δε可通过NDVI来计算,其算式如下[18]:
| ${\varepsilon _4} = 0.9897 + 0.29\ln \left( {NDVI} \right)$ | (4) |
| $\begin{array}{l} \Delta \varepsilon = \left( {{\varepsilon _4} - {\varepsilon _5}} \right)\\ \quad \; = 0.01019 + 0.01344\;\ln \left( {NDVI} \right) \end{array}$ | (5) |
| $\varepsilon = \left( {{\varepsilon _4} - {\varepsilon _5}} \right)/2$ | (6) |
式中,ε4、ε5分别为AVHRR第4、第5通道地表发射率。
1.2 基于地表温度的稀疏植被区域的空气温度遥感估算方法按照地形差异(分为三类:0~500 m、500~1000 m;1000 m以上),根据不同季节无云干扰的NOAA-AVHRR资料反演的TLS和相应时间段的地面气象站1.5 m处观测的空气温度,分别建立了不同高程类型的TLS与空气温度Ta的相关关系(见图 1、图 2、图 3),参与建模的NOAA-AVHRR资料来自中国气象局国家卫星气象中心,资料覆盖范围为中国区域,过境时间分别是2006年3月2日14时27分、2006年11月21日14时39分、2006年12月15日12时15分、2007年5月2日13时37分、2007年6月2日13时18分、2007年7月6日14时9分、2007年8月22日12时45分。

|
图 1 地表温度TLS与空气温度Ta的关系 (NDVI<0.25;高程:0~500 m) Fig. 1 The relation between TLS and Ta (NDVI < 0.25;Elevation: 0~500 m) |

|
图 2 地表温度TLS与空气温度Ta的关系 (NDVI<0.25;高程:500 m~1000 m) Fig. 2 The relation between TLS and Ta (NDVI < 0.25;Elevation: 500~1000 m) |

|
图 3 地表温度TLS与空气温度Ta的关系 (NDVI<0.25;高程:1000 m以上) Fig. 3 The relation between TLS and Ta (NDVI < 0.25;Elevation: above 1000 m) |
从图 1、图 2、图 3可以看出,在稀疏植被地区,TLS与空气温度具有明显的相关性,相关系数R2均超过了0.92,说明在稀疏植被区域可以基于TLS和空气温度的相关关系来推算空气温度。
1.3 基于Vi-Ts的中、高植被覆盖区域空气温度遥感反演方法 1.3.1 “干边”和“湿边”的确定图 4是植被指数与地表温度的散点示意图。假定不同植被指数下的地表温度上限称为“干边”(“Warm Line”), 地表温度下限称为“湿边”(“Cold Line”)。通过植被指数NDVI和地表温度TLS的线性回归,可以分别获取干边、湿边方程,具体如下,
| ${T_{LSNDV{I_{i,\max }}}} = {a_1} + {b_1} \times NDV{I_i}$ | (7) |
| ${T_{LSNDV{I_{i,min}}}} = {a_2} + {b_2} \times NDV{I_i}$ | (8) |

|
图 4 Vi-Ts特征空间示意图 Fig. 4 Sketch map of Vi-Ts |
当NDVIi等于NDVImin时,计算得到的TLSNDVIi.max和TLSNDVIi.min分别对应裸地最大地表温度Tsoil.max和最小地表温度Tsoil.min。当NDVIi等于NDVI max时,计算得到的TLSNDVIi.max和TLSNDVIi.min分别对应最大空气温度Ta.max和最小空气温度Ta.min(在此,假定全植被覆盖条件下,TLS近似于空气温度)。
1.3.2 空气温度的确定首先根据“干边”和“湿边”方程,分别求算任意NDVIi下的TLSNDVIi.max和TLSNDVIi.min。然后根据图 4的梯形几何关系,可以推断NDVIi下的空气温度,具体公式如下:
| ${T_a} = \frac{{{T_{LSNDV{I_i}}} - {T_{LSNDV{I_{i.min}}}}}}{{{T_{LSNDV{I_i}}} - {T_{LSNDV{I_{i.\min }}}}}}\left( {{T_{a.\max }} - {T_{a.\min }}} \right)$ | (9) |
对于稀疏植被覆盖区域,挑选未参与建模的中国区域NOAA-AVHRR遥感资料,成像时间分别是2007年5月4日14时49分、2007年5月20日13时52分、2007年7月21日14时57分,利用已经建立的遥感统计模式来推算空气温度。从图 5和表 1的结果可以看出,遥感统计模式的精度较高,平均绝对误差在1.5~1.8 ℃之间,相关系数在0.9以上。
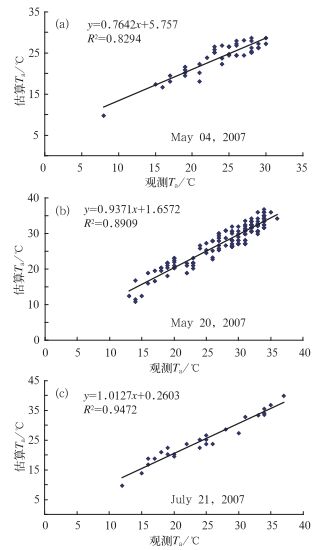
|
图 5 稀疏植被区反演的空气温度与实际观测值的比较 (a) 2007年5月4日;(b) 2007年5月20日;(c) 2007年7月21日 Fig. 5 Comparison of air temperatures in sparse vegetation regions between inversed from remote sensing data and observed at ground meteorological stations (c) |
|
|
表 1 稀疏植被区域的空气温度遥感反演方法的检验 Table 1 Validation of air temperature inversed from remote sensing data in sparse vegetation regions |
对于中、高植被覆盖区域,挑选中国区域晴空范围相对较大的NOAA-AVHRR卫星遥感数据,基于文中第1.3节中提出的空气温度反演方法,获得空气温度的空间网格分布图;同时选择晴空像元对应的相近时间的地面实测空气温度对其反演结果进行检验。参与验证的卫星资料的成像时间分别是2007年8月22日12时45分、2007年7月6日14时9分、2007年6月2日13时18分、2007年5月2日13时37分、2006年3月2日14时27分。比较结果见图 6和表 2,其相关系数达到了0.95,平均绝对误差为1.61℃,样本数为163个。

|
图 6 中、高植被覆盖区反演的空气温度与实际观测值的比较 Fig. 6 Comparison of air temperatures in dense vegetation regions between inversed from remote sensing data and observed at ground meteorological stations |
|
|
表 2 中、高植被覆盖区域的空气温度遥感反演的检验 Table 2 Validation of air temperature inversed from remote sensing data in dense vegetation regions |
文中提出了不同植被覆盖条件下的空气温度卫星遥感估算新方法。在稀疏植被地区,按高程分成三类:0~500 m、500~1000 m、1000 m以上,基于地表温度TLS和地面观测空气温度的相关关系,分别建立了不同高程范围空气温度的遥感估算统计模型。在高植被覆盖区域,基于NDVI和TLS的梯形空间特征关系,建立了空气温度的遥感估算物理模型。
经过实测资料验证表明,本文提出的空气温度遥感估算方法是可行的。稀疏植被区域估算误差在1.5~1.8 ℃之间,估算值与地面实测值的相关系数在0.9以上。高植被覆盖区域,估算空气温度的平均绝对误差为1.61 ℃,相关系数达到了0.95。
本文选取的NOAA-AVHRR卫星资料均是中国气象局北京卫星地面站接收的,覆盖范围为我国中部和东部地区,因此在稀疏植被覆盖区建立的空气温度与遥感反演的地表温度之间的统计关系,不一定适合于我国西部地区。基于地表温度和植被指数空间特征关系的空气温度估算方法是动态的,“干边”和“湿边”方程系数随着卫星资料成像时间的变化而变化。
另外,由于地面空气温度是每3小时观测一次,卫星过境很难与地面观测时间一致,存在一个时间差,在验证过程中,只能选择相近时次的资料进行检验。
廖顺宝, 李泽辉, 游松财, 2003. 气温数据栅格化的方法及其比较[J]. 资源科学, 25(6): 83-88. |
张月维, 何全军, 赵晓利, 等, 2006. 2005年7月珠三角地表温度场的遥感监测分析[J]. 气象, 32(9): 23-27. DOI:10.7519/j.issn.1000-0526.2006.09.004 |
Wan Z M. MODIS land surface temperature algorithm theoretical basis document (LST ATBD)[OL].version3.3. 1999. http://eospso.gsfc.nasa.gov.
|
Kerr Y H, Lagouarde J P, Imberton J, 1992. Accurate land surface temperature retrieval from AVHRR data with use of an improved split window algorithm[J]. Remote Sensing of Environment, 41: 197-209. DOI:10.1016/0034-4257(92)90078-X |
Wan Z M, Feng Y Z, Zhang Y L, et al. land-surface temperature and emissivity retrieval from MODIS Airborne Simulator(MAS) data[C]. Summaries of the seventh JPL Airborne Earth Science workshop 1998. 3:57-66.
|
Chen E, Allen L H, Bartholic J F, et al, 1983. Comparsion of winter-noctual geostationary satellite infrared-surface temperature with shelter-height temperature in Florida[J]. Remote Sensing of Environment, 13: 313-327. DOI:10.1016/0034-4257(83)90033-0 |
Horiguchi I, Tani H and Motoki T. Accurate estimation of 1.5 m-height air temperature by GMS IR data[C]. Pro 24 th Int. Cymp. On Rem. Sens. Envir. Rio de Janeiro May 1991, 301-307, 1992.
|
Green R, 2002. The potential of Pathfinder AVHRR data for providing surrogate climatic variables across africa and Europe for epidemiological applications[J]. Remote Sensing of Environment, 79(2-3): 166-175. DOI:10.1016/S0034-4257(01)00270-X |
Nemani RR and Running SW, 1989. Estimation of resistance to evapotranspiration from NDVI and thermal-IR AVHRR data[J]. Journal of Climate and Applied Meteorolog, 28: 176-294. DOI:10.1175/1520-0450(1989)028<0176:EOSWOT>2.0.CO;2 |
Saravanapavan T and Dye D G. 1995. Satellite estimation of environmental variables by the contextual analysis method: validation in seasonal tropical environment[G]. Global Engineering Laboratory Institute of Industrial Science University of Tukyo, Janpan, 1995.
|
Prince S D and Goward S N, 1995. Global primary production: a remote sensing approach[J]. Journal of Biogeography, 22: 2829-2849. |
Czajkowski K P, Mulhern T, Goward S N, et al, 1997. Biospheric environmental monitoring at BOREAS with AVHRR observations[J]. Journal of Geophysical Research, 102: 29651-29662. DOI:10.1029/97JD01327 |
Prihodko L, Goward S N, 1997. Estimation of air temperature from remotely sensed surface observations[J]. Remote Sensing of Environment, 60: 335-346. DOI:10.1016/S0034-4257(96)00216-7 |
韩丽娟, 王鹏新, 王锦地, 等, 2005. 植被指数-地表温度构成的特征空间研究[J]. 中国科学D辑地球科学, 35(4): 371-377. |
Wan Z M and Dozier J, 1996. A generalize split-window algorithm for retrieving land-surface temperature from space[J]. IEEE Transactions on Geoscience and Remote Sensing, 34(4): 892-905. DOI:10.1109/36.508406 |
刘玉洁, 杨忠东, 2001. 遥感信息处理原理与算法[M]. 北京: 科学出版社.
|
Ulivieri C, Castronuovo MM, Francioni R, et al, 1994. A split window algorithm for estimating land surface temperature from satellites[J]. Advances in Space Research, 14(3): 59-65. DOI:10.1016/0273-1177(94)90193-7 |
Josef C, Hung L, Li Z Q, et al, 1997. Multitemporal, mulitichannel AVHRR datasets for land biosphere studies-arti-facts and correction[J]. Remote Sensing of Environment, 60: 35-57. DOI:10.1016/S0034-4257(96)00137-X |
 2010, Vol. 36
2010, Vol. 36 