引言

自20世纪80年代前后以来，关于位涡的理论和应用的研究蓬勃发展。位涡理论被广泛地应用于天气分析预报和研究工作中。本文主要对位涡理论的一些要点，包括位涡的定义、特性、分析方法、位涡思想、位涡反演、湿位涡以及位涡理论的发展和应用等作一简要介绍。

1 位涡的概念

位涡是“位势涡度(Potential Vorticity)”的简称，通常写为PV。早在20世纪40年代初，Rossby就提出了位涡的概念，他指出在正压条件下，绝对涡度的垂直分量ζ_a与气柱的高度h之比值为一常数，即

${\zeta _a}/h = {\text{常数}}$

(1)

这里，ζ_a/h即为“位涡”最简单的表达形式，它表明位涡是一个既与大气的涡度(旋转性)有关，又与大气的位势(厚度或高度)有关的物理量。在天气学中常用ζ_a/h＝常数，即位涡守恒的理论来解释低压(槽)上山时减弱，下山时加强的现象，这是位涡理论应用中最为人们熟悉的例子之一。

与Rossby同一时期，Ertel也提出了一个位涡的表达式：

$q = \alpha {\mathit{\boldsymbol{\zeta }}_a} \cdot \nabla \theta $

(2)

其中θ为位温，α(=ρ^-1)为比容，ζ_a为绝对涡度矢量，q称为Ertel位涡，或称为广义位涡。Rossby提出的位涡只是Ertel位涡的一个特例。广义位涡在绝热、无摩擦的干空气中具有严格的守恒性(即dq/dt=0)。由式(2) 可见，q是绝对涡度矢量与位温梯度矢量的点乘积。在静力平衡条件下，q可以简化为绝对涡度垂直分量与静力稳定度的乘积:

$q = \left( {{\zeta _\theta } + f} \right)\left( { - g\frac{{\partial \theta }}{{\partial p}}} \right)$

(3)

其中, ζ_θ为等熵面涡度垂直分量，f是地转涡度的垂直分量， $\left( {\frac{{\partial \theta }}{{\partial p}}} \right)$ 为静力稳定度，g为重力加速度。式(3) 也可写为：

$PV = {\sigma ^{ - 1}}{\zeta _{a\theta }}$

(4)

其中，

$\sigma = - {g^{ - 1}}\partial p/\partial \theta > 0$

(5)

${\zeta _{a\theta }} = f + {\zeta _\theta }$

(6)

σ为在xyθ空间中的气块密度，θ为位温，g为重力加速度，ζ_aθ为等熵绝对涡度，在等熵面上的位涡称为等熵位涡(IPV)。

对于典型的中纬度天气尺度系统，ζ＜f，因此，式(3) 可简化为：

$q \approx - gf\frac{{\partial \theta }}{{\partial p}}$

(7)

同时, ∂θ/∂p≈-10 K/100 hPa。在北半球，f＞0，因此通常q为正值，而且可以由下式估算其数量级：

$\begin{gathered} q = - \left( {10\;{\text{m}}/{{\text{s}}^2}} \right)\left( {{{10}^{ - 4}}/{\text{s}}} \right)\left[ { - \frac{{10\;{\text{K}}}}{{10\;{\text{kPa}}}}} \right] \times \hfill \\ \quad \quad \frac{{1\;{\text{kPa}}}}{{{{10}^3}\;{\text{kg}} \cdot {\text{m}}/\left( {{{\text{s}}^2} \cdot {{\text{m}}^2}} \right)}} \hfill \\ \quad = {10^{ - 6}}\;{{\text{m}}^2} \cdot {\text{K}} \cdot {{\text{s}}^{ - 1}} \cdot {\text{k}}{{\text{g}}^{ - 1}} = 1\;{\text{PVU}} \hfill \\ \end{gathered} $

(8)

PVU为“位涡单位”。

由式(7) 可见, 位涡大小与f和 $\left( {\frac{{\partial \theta }}{{\partial p}}} \right)$ 的大小成比例, 而后二者又与纬度和高度相关, 因此位涡的分布一般呈现由低纬向高纬和由低层向高层增大的现象。在对流层中位涡一般小于1.5 PVU，在对流层顶附近位涡突然增大至4 PVU，在平流层中位涡随高度迅速增大, 通常称为“高位涡库”; 在对流层低层赤道附近位涡近于0 PVU，中纬地区约0.3 PVU, 在对流层高层中纬度地区位涡典型值为1.0 PVU。PV=2 PVU的等值线通常代表来自低纬地区对流层的低位涡大气与来自高纬地区对流层高层及平流层的高位涡大气之间的边界。在副热带急流以北地区, PV=2 PVU的等位涡面接近于实际大气的对流层顶, 一般称之为“动力对流层顶”。

2 位涡的守恒性

如上所说，位涡是绝对涡度与位温梯度的乘积。其中，位温是一个描述空气的热力状态的物理量，而涡度则是一个描述大气旋转性(包括旋转方向和强度)的物理量，因而位涡便是一个既包含热力因子又包含动力因子的综合的物理量。

涡度是一个三维矢量，通常主要关心其垂直分量。当大气运动是非地转的，即有辐合或辐散时，绝对涡度不是一个守恒量。由涡度方程可知，当有辐合时，涡度增大，辐散时，涡度减小。而且由大气连续方程可知，水平散度又是与垂直运动相联系的。一个垂直气柱若保持质量不变，则当其水平方向收缩时，垂直方向便拉长；相反，当其水平方向扩大时，垂直方向便缩短。假设地面的垂直速度w₀=0，则当对流层低层有水平辐合时，便有垂直上升运动产生；而当有水平辐散时，则有垂直下沉运动。所以当一个作气旋性旋转的气柱收缩(辐合)时，气柱拉长，涡度增大，旋转加快。绝对涡度包括相对涡度和地转涡度两部分，而对局地而言，地转涡度f为常数，所以绝对涡度增大也就是相对涡度增大；相反，当气柱扩大(辐散)时，气柱缩短，涡度减小，旋转变慢，局地相对涡度减小，或反气旋涡度增大。

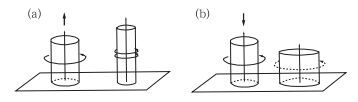
由上分析可见，涡度大小与气柱长短成正比的关系，即气柱拉长时涡度增大，气柱缩短时涡度变小(图 1)，涡度的垂直分量与气柱的高度之比值保持常数。而涡度大小与气柱长短两者的比值，就是Rossby所定义的位涡，说明它是一个守恒量。

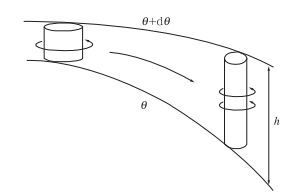
现在再来看一个旋转的小气柱(涡柱)作等熵运动时涡度变化的情况。假定有一个旋转的小气柱，如图 2所示，其底面位于位温为θ的等位温面上，顶面位于位温为θ+Δθ的等位温面上，小气柱的上下界面之间的位温差为Δθ，气柱的厚度为h。设小气柱在两个等位温面之间干绝热地作下降运动，并保持其质量不变，由于Δθ保持常数，则如果气柱厚度增大，θ的垂直梯度便减小。另一方面，由于气柱拉长，产生上升运动，使水平辐合加大，气柱收缩，涡度增大，旋转加快。在这种变化过程中，随着气柱下降，气柱不断拉长，静力稳定度变得愈来愈小，但是涡度却变得愈来愈大，因而涡度垂直分量与静力稳定度两者的乘积，也就是由公式(3) 所定义的小气柱的位涡 $q = \left( {{\zeta _\theta } + f} \right)\left( { - g\frac{{\partial \theta }}{{\partial p}}} \right)$ ，则始终是保持不变的，同样说明位涡的守恒性。由于在上面的讨论中设定Δθ为常数，所以在这种情况下，公式(3) 中的 $\left( {{\zeta _\theta } + f} \right)\left( { - g\frac{{\partial \theta }}{{\partial p}}} \right)$ 与公式(1) 中ζ_a/h两者是基本一致的, 由此可见, 正如前面所说，Rossby提出的位涡只是Ertel位涡的一个特例。

3 位涡的分析

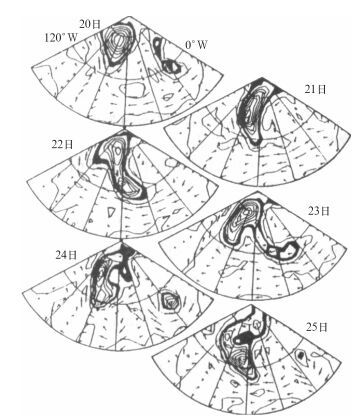
位涡有多种分析方法，最常用的方法之一是等熵位涡分析法，即在等位温面(即等熵面)上分析等位涡线。等熵面一般取为与极锋地区的对流层顶相重合的等位温面。在北半球冬季一般取θ=315 K，夏季一般取θ=325 K的等位温面。由于如上所说, 位涡具有守恒性，即在绝热、无摩擦条件下，运动大气的位涡保持不变。因此它是一个很好的示踪器。可以通过追踪位涡异常区(即位涡高值或低值区)来追踪大气扰动的演变情况。图 3给出了一个例子，它显示了1982年9月20—25日在300 K等熵面图上，40°N至北极、120°W~0°，以60°W为中心经度的区域内等熵位涡高值区从西北向东南伸展并断裂的过程。通过IPV高值区的演变图的分析，我们可以很清楚地看到一个具有高IPV值的空气团的时空变化过程。

4 位涡思想

位涡具有两个重要特性, 除了上面所说的守恒性以外，还具有可反演性。所谓“可反演性”, 即在给定位涡分布和边界条件，并假定运动是平衡(如地转风平衡、热成风平衡、梯度风平衡等)的情况下，可以反演出同一时刻的风、温度、位势高度等物理量的分布来。Hoskins等^[1-2]利用位涡守恒性和可反演性的原理，通过等熵位涡分析很好地解释了准平衡运动的动力学特征，清楚地显示了高空位涡异常和低层位温异常所对应的高低空系统的结构特征和演变趋势。这种分析理论和方法称为位涡思想(PV thinking)。

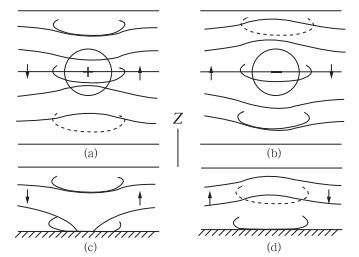
图 4为理想的高空正、负位涡异常区和低层正、负位温异常区所对应的高低空系统的结构特征的示意图。图 4a表示在高空有正位涡异常区的情况下，由于在正位涡异常区内位涡比周围高，即是一个涡度和静力稳定度大值区，因此在正位涡异常区内等位温面向正位涡异常中心收拢，造成与在正位涡异常中心的上方和下方相邻的等熵面之间的距离拉大，致使那里的静力稳定度减小。由于位涡守恒性的作用，使气旋性涡度增大，结果便出现围绕正位涡异常区的气旋性环流。图 4b表示在高空有负位涡异常区的情况下，与上述情况相反, 由于在负位涡异常区内位涡比周围低，即为一个涡度和静力稳定度小值区，因此在负位涡异常区内等位温面向负位涡异常中心分开，造成与在负位涡异常中心的上方和下方相邻的等熵面之间的距离缩短，致使那里的静力稳定度增大, 气旋性涡度减小, 反气旋性增大，结果便出现围绕负位涡异常区的反气旋性环流。图 4c表示在位涡均匀分布的低层有正温度异常出现的情况下，各等熵面间的间隔加大，使静力稳定度减小，因而气旋性涡度增大，结果便出现围绕正温度异常区的气旋性环流。类似地, 在低层有负温度异常出现的情况下，各等熵面间的间隔减小，使静力稳定度增大，因而引起反气旋性涡度增大，结果便出现围绕负温度异常区的反气旋性环流(如图 4d所示)。上述等熵位涡思想也可通过图 5得到清楚的表示。

上述等熵位涡思想包含下列要点：(1) 用涡度观点，我们通常将大气结构看成是由移动性的高空槽、脊叠加在地面气旋、反气旋之上所组成的。而用位涡思想则将大气结构看成是由高空位涡异常和低层位温异常相叠加而组成的；(2) 围绕高空正、负位涡异常区，分别有气旋性和反气旋性环流出现；而近地面层的正、负温度异常区，也分别有气旋性和反气旋性环流相对应。上下层位涡和温度异常所诱生的风场之和便构成了总风场；(3) 在绝热、无摩擦假定下等熵面上位涡平流引起位涡的局地变化；(4) 位涡和温度异常所诱生的风场改变了等熵位涡的分布；(5) 等熵位涡的分布又与新诱生的风场相联系。位涡和温度异常与诱生的风场的连续相互作用，造成“自我发展”(self development)过程，这种过程将一直延续到高低层异常区的轴线在同一垂直线上为止。

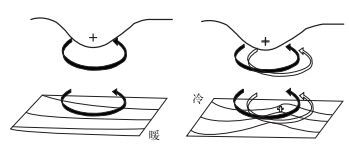
利用等熵位涡思想可以很好地解释地面气旋的发展过程。如图 6所示, 当高空有一正位涡异常区(与对流层顶下降相对应)东移叠加在低空原先存在的地面锋区上空时，在正位涡异常区可诱生出一个气旋性环流并向下伸展(其垂直伸展的尺度H_R称为Rossby穿透高度， ${H_R} = f\frac{L}{N}$ ，其中f, L, N分别为地转参数、水平尺度和浮力频率)。气旋性环流与低层锋区作用造成冷暖平流。暖平流引起低空正位温异常，从而在原来的低空气旋性环流的前方诱生出附加的气旋性环流，它又使高层的气旋性环流加强，而高层的气旋性环流又促使低空的气旋性环流和温度平流加强，结果便造成地面气旋的发展。这种正反馈过程将一直延续至上下层的两个异常区的轴线在同一垂直线上时才会终止。

5 位涡反演

如前所述，位涡具有可反演性, 即可由给定位涡的分布及其变化，反演诊断出风、温度、位势高度等要素的分布及其变化。位涡反演理论最早由Kleischmidt^[3-6]提出。他用流体静力原始方程模式位涡反演得出如下的结论:

(1) 高位涡区引起正环流, 低位涡区引起负环流;

(2) 激发的流场向位涡异常区上、下扩展，扩展尺度由Rossby穿透高度决定；

(3) 高位涡区内静力稳定度、绝对涡度都较大，低位涡区则相反；

(4) 高位涡区的上、下方静力稳定度都减小，低位涡区则相反；

(5) 向前移动的高位涡对它下层大气像个“吸尘器”，吸进前缘处空气向上运动，并向后缘挤压产生下沉运动。

可是由于Kleischmidt的观点太超前于当时的理论发展，而被人们忽视。后来Hoskins等^[2]再次提出位涡反演理论和位涡思想，位涡反演才受到重视。

位涡反演原理的独到之处在于，它能定量诊断出与反映各种动力学过程的PV扰动相联系的位势扰动、温度扰动和风场扰动，通过分析这些扰动的强度及其相互作用，不仅能诊断出决定系统发展的主要动力因子，而且能有效地揭示出系统发展演变的物理机制。

最近二三十年来，关于位涡反演的理论发展很快，提出很多位涡模式(如浅水模式、准地转模式、半地转模式、流体静力原始方程模式、非流体静力模式等)和反演方法(如具有圆形轴对称结构位涡异常区的反演、准地转位涡反演以及分段位涡反演等)。下面仅对其中的分段位涡反演法(piecewise PV inversion，简称PPVI)作简要介绍。

大气运动是包含各种尺度的、非常复杂的非线性过程。分段位涡反演方法是一种具有丰富动力学内涵的诊断方法。它通过把复杂的现象“分解”成各种相对简单的现象, 以便于研究天气现象间内在的“因果”关系。

分段位涡反演方法的具体做法是, 首先将整个位涡场人为地分成个别位涡异常区和周围环境场, 然后逐个地反演位涡异常区, 分析其对整个流场的贡献以及它们之间的相互作用。换句话说，若某一天气现象发生时会出现多个位涡异常, 采用分段反演方法就能诊断出哪些位涡异常是产生该现象的主要原因, 从而推断出该现象可能的动力学机制。

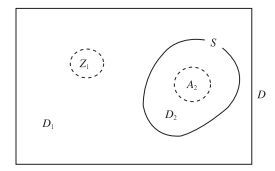
为了清楚起见, 我们再稍微具体地描述一下分段位涡反演(PPVI)技术。设通过观测, 已知在一个区域D (如图 7所示)中的流函数为ψ_ob(x, y, z), 相应的位涡为q_ob以及q_ob的异常为q′_ob。假定在区域D中包含D₁和D₂两个区域，D=D₁+D₂。其中D₂区中的位涡扰动q′=0，而D₁区中的位涡扰动q′=q′_ob。D₂区和D₁区的分界线为S，在S线上q′是不连续的。然后通过反演q场，就可以获得流函数ψ(x, y, z)。例如，假定在D₁中有正的PV异常Z₁，就可以通过PPVI来估计在D₂中引起的风，以及与这种风造成的在D₂中的PV异常A₂。假定在区域D中包含多个位涡异常区，然后逐个地进行反演，这就是所谓的分段反演。根据位涡方程可知，有很多因子可能引起位涡非守恒过程，从而分别引起位涡异常, 借助分段反演方法可以诊断出每种因子各自对风、压场变化的贡献，从而有助于理解天气系统演变的原因和本质。

6 湿位涡的分析

在考虑降水特别是暴雨的生成机制时，必须考虑水汽的作用, 从而出现了湿位涡概念。对潮湿大气，以相当位温θ_e代替位温θ, 则可得湿位涡MPV的表达式:

$MPV = a{\zeta _a} \cdot \nabla {\theta _e}$

(9)

同样可给出湿位涡在等压坐标和等熵坐标中的简化表达式, 分别为：

$\begin{gathered} MPV = - g\left( {f\mathit{\boldsymbol{k}} + {\nabla _p} \times \mathit{\boldsymbol{V}}} \right) \cdot {\nabla _p}{\theta _e} \hfill \\ \quad \quad \;\; = - g{\zeta _p}\frac{{\partial {\theta _e}}}{{\partial p}} - g\mathit{\boldsymbol{k}} \times \frac{{\partial \mathit{\boldsymbol{V}}}}{{\partial p}} \cdot {\nabla _p}{\theta _e} \hfill \\ \end{gathered} $

(10)

$MPV = - g{\zeta _\theta }\frac{{\partial {\theta _e}}}{{\partial p}}$

(11)

其中, ζ_p和ζ_θ为ζ_a在垂直方向的投影。如果不计非绝热加热和摩擦效应，湿位涡同样具有守恒性。湿位涡这一物理量不仅表征了大气动力、热力属性，而且考虑了水汽的作用，所以对湿位涡进行诊断，可以寻求各热力和动力及水汽条件与降水的关系，从而揭示降水发生、发展的物理机制。近年来湿位涡概念得到广泛的应用。

在式(10) 右边有两项，由此可见，湿位涡可以分解为湿正压项(MPV1) 和湿斜压项(MPV2)，即:MPV=MPV1+MPV2。其中 $MPV1 = - g\left( {\zeta + f} \right)\frac{{\partial {\theta _e}}}{{\partial p}}$ ，表示惯性稳定性(ζ+f)和对流稳定性 $\left( {\frac{{\partial {\theta _e}}}{{\partial p}}} \right)$ 的作用。当惯性稳定(ζ+f>0) 和对流稳定 $\left( {\frac{{\partial {\theta _e}}}{{\partial p}} ＜ 0} \right)$ 时, MPV1>0。

$MPV2 = g\left( {\frac{{\partial v}}{{\partial p}}\frac{{\partial {\theta _e}}}{{\partial x}} - \frac{{\partial u}}{{\partial p}}\frac{{\partial {\theta _e}}}{{\partial y}}} \right)$ ，包含了湿斜压性(∇_pθ_e)和水平风垂直切变的贡献。将等压面位涡分解为正压部分和斜压部分，可以计算出(湿)斜压系统中(湿)斜压性相对于正压性的大小，从而反映(湿)斜压系统的结构特征。为更好地反映湿位涡与降水的关系，类似于相对涡度、牵连涡度的概念，也可以提出相对湿位涡和牵连湿位涡的概念，相对湿位涡的表达式为：

${\left( {MPV} \right)_{re}} = - g\zeta \frac{{\partial {\theta _e}}}{{\partial p}} + g\left( {\frac{{\partial v}}{{\partial p}}\frac{{\partial {\theta _e}}}{{\partial x}} - \frac{{\partial u}}{{\partial p}}\frac{{\partial {\theta _e}}}{{\partial y}}} \right)$

(12)

牵连湿位涡即为大气静止时(u=0, v=0) 的湿位涡，因此也可以说是大气的背景湿位涡，其表达式为：

${\left( {MPV} \right)_{am}} = - gf\frac{{\partial {\theta _e}}}{{\partial p}}$

(13)

很明显，相对湿位涡相当于从湿位涡MPV中减去大气的背景位涡，因此可以称相对湿位涡为大气的扰动湿位涡。

将湿位涡分解为相对湿位涡和牵连湿位涡，则为在随地球旋转的坐标系中考察斜压涡旋的特征提供了方便，正是相对湿位涡这个物理量简明而定量地反映了强对流系统发展的动力学成因。

7 位涡理论的发展与应用

最近二三十年来，位涡理论和应用研究发展很快。回顾历史，其发展进程大致可以分成两个阶段：第一阶段始于20世纪80年代初，Hoskins等^[2]提出了绝热无摩擦大气有沿等熵面做二维运动的趋势以及位涡所蕴藏的丰富动力学内涵(即位涡反演原理)，因而等熵面位涡图是研究大气动力学过程一个非常有用的工具。运用上述理论，对切断低压、阻塞高压的空间结构、起源及维持，Rossby波的传播，斜压、正压不稳定机制等给出明晰的物理图像和解释。第二阶段始于20世纪90年代初，Davis^[7]提出了分段位涡反演方法。利用位涡守恒性可以分离出主要由非守恒过程引起的位涡异常，借助分段反演方法可以诊断出各自对风、压场的贡献，从而推断出某些现象产生的原因和本质特征。这方面的研究工作主要用准地转位涡和Ertel位涡并且集中在以下两个领域：第一，利用观测资料和理论模型对气旋生成和锋面内次级环流等动力学机制进行定量化诊断研究；第二，利用观测和模式预报得出的位涡偏差，反演出动力协调的风、气压、温度场，叠加到原来初始场中改进初始场，达到提高短期预报准确度的目的。

位涡的理论及其应用研究还有更多方面的进展，以下仅对其中很少的一部分作十分简要的介绍：

(1) 用以判定大气的对称不稳定性，解释锋面雨带的生成

位涡q的表达式也可以写成：

$q = {N^2}{F^2} - {S^4}$

(14)

其中， ${N^2} = \frac{g}{{{\theta _0}}}\frac{{\partial \theta }}{{\partial z}},{F^2} = f\left( {f + \zeta } \right),{S^2} = f\frac{{\partial \mathit{\boldsymbol{V}}}}{{\partial z}}$ 分别表示静力稳定性、惯性稳定性和大气斜压性。所以位涡的大小和正负与大气的各种静力和动力稳定性紧密相关。

Bennets等^[8]提出了条件性对称不稳定，即湿静力-惯性不稳定性的概念，并提出当湿位涡(q_w)为负值(q_w＜0) 时就可能出现条件性对称不稳定。他们很好地解释了锋面中尺度雨带的发生和发展的原因。Xu^[9]研究了准地转位涡(GPV)与带状降水的关系，并用模式说明了出现单条雨带和多条雨带的不同情况以及它们形成、维持的机制。

(2) 分析有利于形成对称不稳定的天气形势

Bennetts等^[8]还根据湿球位涡变化方程来讨论有利于形成对称不稳定的天气形势。他们指出在绝热、无摩擦情况下，湿球位涡q_w的倾向方程可简化为

$\frac{{{\rm{d}}{q_w}}}{{{\rm{d}}t}} \approx f\left( {{g^2}/\theta _0^2} \right)\mathit{\boldsymbol{k}} \cdot \left( {\nabla {\theta _w} \times \nabla \theta } \right)$

(15)

当f(g²/θ₀²)k·(∇θ_w×∇θ)＜0时, $\frac{{{\text{d}}{q_w}}}{{{\text{d}}t}} ＜ 0$ 。这说明当沿热成风方向湿度增大时, 有利于形成条件性对称不稳定，从而很好地解释了锋面中尺度雨带的发生和发展的一种可能机制。同时Bennets等指出在初始为静(重)力稳定、惯性稳定(即MPV1>0) 的情况下，只有当MPV2＜0时才可能出现对称不稳定，说明湿斜压性和水平风垂直切变对形成对称不稳定的重要作用。

(3) “位涡下传”理论及对流层下部及地面的气旋发展

Hoskins等论证了对流层的上部或平流层的位涡扰动下传，可以引起对流层下部及地面的气旋发展。高低层的位涡和温度扰动, 以及它们诱发的环流共同作用的结果, 便造成了低涡或气旋的发生和发展。并再次提出和讨论了Kleinschmidt早在20世纪50年代就已提出的位涡反演理论及其意义。Davis等^[10]提出可以将高层对流层锋视为等熵面上的PV梯度加强的过程。Davis等^[11]提出了一个观点，认为高层位涡的发展强烈受到低层异常的影响。Molinari等^[12]分析了热带风暴Danny与一个高层对流层正的PV异常间的相互作用，提出叠加原理，即小尺度的正的高层PV异常与低层热带气旋中心相叠加使得热带气旋加强，特别指出高层大尺度的PV扰动并不利于气旋生成。Molinari等^[12]的叠加原理发展和深化了Hoskins的位涡下传理论。吴国雄等^[13-14]从原始方程出发，在导出湿位涡方程的基础上，证得绝热无摩擦的饱和大气具有湿位涡守恒的特性，并由此去研究湿斜压过程中涡旋垂直涡度的发展，提出倾斜涡度发展(SVD)理论，在暴雨等强天气研究中得到广泛应用。

(4) 干侵入理论的应用

干侵入(dry intrusion)指的是来自平流层下层和对流层中上层的以低相对湿度和高位涡表征的干燥下沉气流，它们可以与对流层低层暖湿空气相互作用。这种现象也称为高层高位涡侵入或对流层顶折叠。根据位涡守恒原理，来自高层稳定环境的高位涡气流到达低层不稳定环境后其涡度增大，于是便会促进气旋的发生和发展，有利于引起暴雨或强对流天气的形成。阎凤霞等^[15]与姚秀萍等^[16]分析了干侵入对气旋发生发展以及暴雨过程的作用。

(5) 湿位涡物质不可渗透性理论及应用

自Hoskins等^[2]提出位涡反演理论后，又一个重要进展是Haynes^[17]提出了“位涡物质(PVS)”概念。所谓位涡物质，即具有一定位涡的空气物质, 它们就像任何化学物质一样，可以被平流，它们具有保守性和不渗透性(impermeability)。等熵面是一个物质面，相当于一层半透明薄膜。一般空气物质可以自由通过等熵面，而“位涡物质”则不能穿过等熵面，只能在各层等熵面内作准二维运动。“位涡物质”具有守恒性，除非等熵面与边界面(如地面)相交，“位涡物质”像电荷一样不会自我毁灭，但可以被稀释或浓缩。以上两结论是在非流体静力、非绝热、甚至有摩擦存在的情况下导出的，具有广泛的适用性。

高守亭等^[18]还从由完全动力学方程推出的湿位涡方程得到湿位涡物质不可渗透性理论。由于位涡物质具有这些重要特性，因此位涡理论在天气系统移动和发展分析预报方面有着广泛的应用。特别是对大尺度运动来说，由于在直角坐标系中位温面与水平面是近似平行的，涡度矢量和位温梯度矢量的交角较小，两个矢量点乘的积是明显的。因此对许多中高纬度天气系统的发展和演变来说，位涡是一个非常有效的动力示踪工具。对中尺度系统的发展和演变的研究来说，位涡也有广泛的应用。但在深对流系统中，由于湿等熵面的倾斜，位温梯度矢量与涡度矢量的交角变大，极端时可接近垂直(~90°)，因此两个矢量的点乘积变小，位涡变得较弱。针对这个问题，高守亭等^[19-22]将位涡的定义广义化，引入了对流涡度矢量(CVV)和湿涡度矢量(MVV)这样两个新概念：

$CVV = \left( {{\mathit{\boldsymbol{\zeta }}_a} \times \nabla {\theta _e}} \right)/\rho $

(16)

$MVV = \left( {{\mathit{\boldsymbol{\zeta }}_a} \times \nabla {q_v}} \right)/\rho $

(17)

其中, ζ_a为绝对涡度矢量, θ_e为相当位温, q_v为比湿, ρ为密度。他们把对流涡度矢量和湿涡度矢量这样两个新物理量应用在二维云分辨模式及三维云分辨模式中，来研究热带对流系统，得到了有意义的研究成果。特别指出CVV和MVV的垂直分量与热带对流密切相关，并且能把热带对流的中尺度动力过程和热力过程与云微物理过程密切联系起来。因此提出了一种很有应用潜力的诊断分析方法。

(6) 在天气诊断分析和预报中的应用

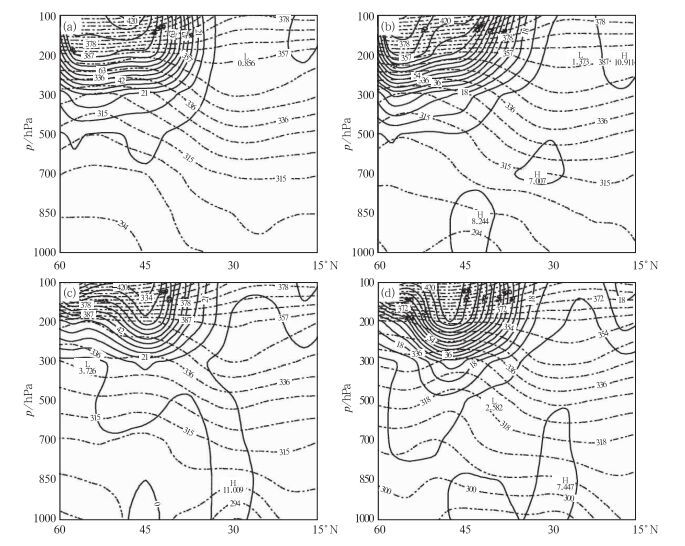
在国内，自20世纪80年代以来，位涡的研究主要是将PV作为一个诊断量用于对暴雨和其他天气系统的诊断。例如王永中等^[23]研究了暴雨与低层流场位涡的关系问题，发现暴雨区基本上和高值位涡区相重合或者靠的很近，并且二者的发展过程也比较一致。刘还珠等^[24]通过一个强降水个例分析了湿位涡与锋面强降水天气的关系，指出可利用对流层低层湿位涡的符号与数值来判断强降水的落区。候定臣^[25]分析了夏季江淮气旋活动的等熵面位涡图和位涡垂直廓线，探讨了夏季江淮气旋发生、发展的可能机制，提出夏季江淮地区气旋波活动的一个概念模式，即从高原一带东移的对流层中层弱的扰动在有利条件下引起江淮地区较强降水，中层潜热释放导致气旋性环流向下延伸，最终可在地面静止锋上形成波动。并指出，来自中高纬平流层下部的高位涡空气沿等熵面向南方下滑，是典型温带气旋区别于夏季江淮气旋的主要特征。陆尔等^[26]应用位涡分析讨论了1991年江淮特大暴雨冷空气活动的特征，指出南下的冷空气在江淮一带被来自低纬西南暖气流和东南暖气流所切断，形成高位涡冷空气中心，它与两支暖气流相互作用，维持梅雨锋，从而形成持续暴雨。吴海英等^[27]研究了在1991年7月5—6日的江淮暴雨过程中位涡扰动与气旋发展的关系，通过对等压面位涡的垂直结构演变的分析发现，高层位涡的下传，促进了对流层低层及地面的气旋发展(图 8)。寿绍文等^[28]和王淑云等^[29]分析了在层结对流性稳定条件下产生的暴雨过程，根据对称不稳定机制解释了暴雨的成因。由于暴雨和强对流天气的发生需要具备水汽、不稳定能量和动力抬升等条件，而从上面介绍的理论和应用实例可见，通过位涡分析可以全面地反映这些条件，因此位涡理论在暴雨和强对流等天气的诊断分析和预报中常常得到广泛的应用^[30-59]。

8 小结

综上所述，位涡理论发展到今天，已成为天气动力学领域中的重要研究方法之一。位涡守恒性和可反演性成为利用位涡理论描述大气动力学过程的两个主要原理。等熵位涡(IPV)概念简捷地概述了通常以平流、辐散和垂直运动来描述的所有的平衡动力学，IPV思想加深了我们对天气系统特征的理解。正如涡度在正压大气中的作用一样，位涡对于研究斜压大气中的天气现象来讲，是一个十分有用的工具。同时PV概念与理论在数值预报模式的发展和评估中，在大气模式的参数化方案的制定上，也是十分有价值的。特别是对暴雨、强对流等天气现象的物理机制的研究上位涡分析更是常用的重要工具之一。如前所述，无论是对干位涡、湿位涡或是更细致地对它们的组成部分的进一步分析，均有助于加深对暴雨等天气过程的发生、发展和演变规律的理解。