2. 河北省生态环境监测实验室,石家庄 050021
2. Hebei Eco-Environmental Monitoring Laboratory, Shijiazhuang 050021
天气雷达在观测过程中采用的是锥面扫描, 空间定位参数是:R(波束从天线到散射质点所走过的路径长度),θ(天线的方位角),φ(天线的仰角)。在地球大气条件下, 一般说来R是一条曲线的长度, 而且它的曲率是随大气层结的变化而变化。当曲率超过地球表面曲率时,射线由一定的高度反射到地面,再反射上去,如此反复进行,电磁波可以传到很远的地方,这种现象称为大气波导或波导层,产生超折射现象。由超折射现象所产生的回波称为超折射回波, 当大气中发生超折射时, 就会在平面位置显示器上平时无地物回波的距离上出现地物回波。由于超折射现象的存在,使得雷达读得的目标视位置与实际位置产生偏差,往往引起人们对雷达回波空间定位造成误解。
在超折射对电磁波传播的影响研究方面,姚展予等[1]研究了大气波导特征及其对电磁波传播的影响。胡晓华等[2]分析了气象条件对大气波导的影响,讨论了温度、气压、湿度和风、云、雾等天气现象与大气波导的关系,总结了易出现大气波导现象的天气条件。浙江金华地区的雷达观测人员利用常规雷达的观测资料对超折射回波与未来降水的关系进行过初步分析[3]。官莉等[4]利用南京实际观测的超折射回波对大气波导形成条件及传播路径进行了模拟和研究。
华北平原是我国北方冬季大雾出现频率较高的地区,许多学者对华北平原大雾发生的气候和气象条件特征进行了统计和分析[5-8]。本文利用石家庄CINRAD/SA型多普勒天气雷达资料,结合探空实况对2005年11月19-21日(文中时间采用北京时)华北平原大雾天气过程的超折射回波的形成原理进行了电磁射线追踪分析。为进行雷达空间定位和华北平原大雾天气的监测、预报提供新的技术手段和科学依据。
1 华北平原大雾天气实况和多普勒天气雷达超折射回波演变2005年11月19至21日,华北地区出现了大范围的大雾天气,从11月17日开始,河北平原东部京广线以东部分地区有大雾,但范围很小,19日20时,雾区位于河北东南部到山东西北部,20日08时继续扩大,河南大部、山东西部与河北平原为大雾所笼罩,河北省有80多个站出现了大雾天气,河北平原东部、河南北部、山东西北部部分地区雾最浓时能见度不足50 m。下午,雾区的范围和强度减小,雾区主要位于冀东平原和鲁西北。入夜后又开始加强,21日02时雾区进一步扩展,此后一直维持,日出以后,大雾开始逐渐消散,14时,大雾全部消散。
在雷达的平面位置显示产品上,超折射回波一般呈辐射状,有时呈片状,并且回波很强,很像强对流回波,但抬高雷达仰角,超折射回波强度迅速减弱或消失。在卫星云图上这些超折射回波区没有云层,地面观测实况也没有强对流天气出现。根据石家庄CINRAD/SA雷达资料,从2005年11月20日14时开始,在0.5°反射率因子图上方位62°距离128 km开始有超折射回波出现,速度图上显示的速度为零,在1.5°同一位置附近反射率因子图上没有回波。此后超折射回波时现时断, 强度也较弱。
从20日22时30分开始,在0.5°反射率因子图上雷达站东北100~200 km,方位30~60°有较强超折射回波,最大反射率因子强度为35 dBz。速度产品图上相应位置为零速度。
21日02时,超折射回波明显增强,在0.5°反射率因子图上44°~195°,60~400 km有成片的超折射回波出现,并且回波有层次,强中心位于52°,距离雷达站209 km,强度达60 d Bz以上。相应的0.5°速度产品图相应位置为零速度,并有紫色距离模糊区。在1.5°反射率因子图上, 在40°~70°, 200~260 km范围内有25 dBz以下的弱回波, 相应的1.5°速度产品图上为无回波区。
21日08时,超折射回波进一步发展,在0.5°反射率因子图上30°~195°,50~460k m有超折射回波,强中心位于30°~220°, 距离140~220 km,强度在60 dBz以上,在0.5°速度图上相应区域为零速度区,并伴有紫色距离模糊区, 如图 1所示。

|
图 1 石家庄CINRAD/SA雷达2005年11月21日08:03:53反射率因子产品和速度产品 Fig. 1 The reflectivity and velocity products of Shijiazhuang CINRAD/SA radar at 08:03:53 on November 21, 2005 |
超折射回波11时左右开始减弱,13时基本消失,伴随超折射回波的消失,14时大雾也散尽,此时,在反射率因子和速度回波图上均没有回波。
从上面超折射回波出现的时间分布来看, 主要出现在大雾的发展和维持阶段。
2 华北平原大雾天气探空资料分析大气折射与气温、气压和湿度之间的关系为[9]:
| $ N{\rm{ = }}\left( {n - 1} \right) \times {10^6} = \frac{{77.6}}{T}\left( {p + \frac{{4810e}}{T}} \right) $ | (1) |
其中n为大气折射率,N为大气折射模数, T是大气的绝对温度,单位为K,p为气压,e是水汽压,单位为hPa。通常气压、温度和水汽压都随高度而变化。
当电磁波传播距离很短时,可近似认为地球表面为平面,但若电磁波传播距离较长时,就必须考虑地球曲率的影响,此时,为了将地球表面处理成平面,通常对N进行地球曲率订正而引入大气修正折射模数M。由式(1) 可得其表达式为:
| $ M = N + \frac{h}{{{R_m}}} \times {10^6} $ | (2) |
其中Rm=6.371×106 m为平均地球半径,垂直高度h的单位取为m。将式(1)、(2) 两边对高度h求导,可得:
| $ \begin{array}{l} \frac{{{\rm{d}}N}}{{{\rm{d}}h}} = - \frac{{77.6}}{{{T^2}}}\left( {p + \frac{{9620e}}{T}} \right)\frac{{\partial T}}{{\partial h}} + \\ \;\;\;\;\;\;\;\;\;\;\frac{{77.6}}{T}\frac{{\partial p}}{{\partial h}} + \frac{{373256}}{{{T^2}}}\frac{{\partial e}}{{\partial h}} \end{array} $ | (3) |
| $ \frac{{{\rm{d}}M}}{{{\rm{d}}h}} = \frac{{{\rm{d}}N}}{{{\rm{d}}h}} + 0.157 $ | (4) |
当
超折射条件下探测到的地物回波有下面几种类型:(1) 两层模式:当从近地面开始往上存在一超折射层, 而在超折射层之上为非超折射层时, 就使得地物回波从本站开始, 较连续地扩展到数十千米或更远。(2) 三层模式:测站周围近处出现正常的地物回波, 而在远距离处出现一片超折射回波。其相应的层结为:在近地面存在较薄的一层非超折射层, 在此层之上有一超折射层, 再往上又为非超折射层。(3) 四层模式:其相应大气层结由近地面向上依次为:超折射层-非超折射层-超折射层-非超折射层,这种回波比较罕见[9]。
为了进一步分析此次大雾天气及超折射回波形成的原因,利用距离雷达站最近的邢台探空站资料分析气象要素的垂直变化特征,并计算大气折射模数N(实际应用单位)和大气修正折射模数M,计算结果见表 1、表 2和图 2、图 3。
|
|
表 1 2005年11月20日08时邢台探空记录及计算结果 Table 1 The records and calculated results of Xingtai sounding station at 08:00 on November 20, 2005 |
|
|
表 2 2005年11月21日08时邢台探空记录及计算结果 Table 2 The records and calculated results of Xingtai sounding station at 08:00 on November 21, 2005 |
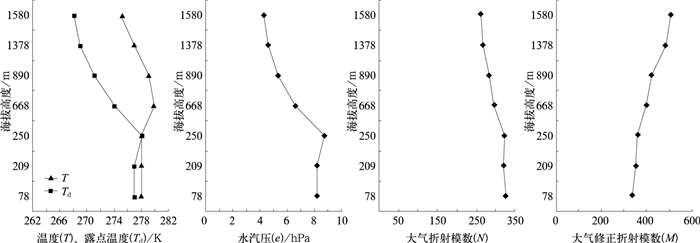
|
图 2 2005年11月20日08:00的温度(T)、露点温度(Td)、水汽压(e)、大气折射模数(N)和大气修正折射模数(M)的垂直廓线分布 Fig. 2 The vertical profile distribution of temperature (T), dew temperature(Td), vapour pressure (e), atmospheric refractive modulus (N), and atmospheric modified refractive modulus (M) at 08:00 on November 20, 2005 |
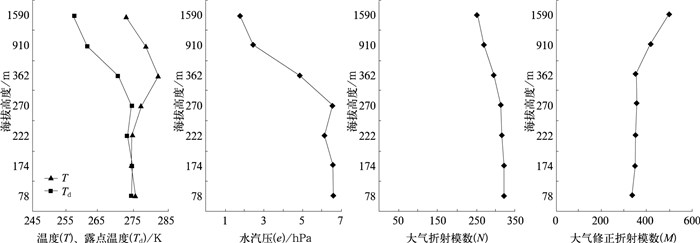
|
图 3 2005年11月21日08:00的温度(T)、露点温度(Td)、水汽压(e)、大气折射模数(N)和大气修正折射模数(M)的垂直廓线分布 Fig. 3 The vertical profile distribution of temperature (T), dew temperature (Td), vapour pressure (e), atmospheric refractive modulus (N), and atmospheric modified refractive modulus (M) at 08:00 on November 21, 2005 |
从图 2可见,20日08时,在250~668 m出现逆温,水汽压从250 m以上递减,M自地面随高度呈上升状态,不满足超折射发生的条件。在图 3中,从222~362 m温度随高度增加,水汽压从222~270 m增加,270 m以上开始减少。M从地面到270 m为增加,270 ~362 m为随高度减少,362 m以上随高度增加。因此,在270~362 m之间存在
从上述两个时次的资料还可以看出,温度和露点温度曲线相距很近,说明整层大气湿度很大,并且均有逆温区,都出现了大雾天气,但前者并没有出现超折射回波,因此,垂直方向出现逆温和湿度随高度递减只是为超折射回波的出现创造了有利条件,只有当达到一定强度才能出现超折射回波。
表 3为2005年11月21日08时位于华北平原边缘的北京、张家口、济南3个周边探空站的探测资料及相应的大气修正折射模数M计算结果,可以看出在超折射回波出现时,这3个探空站上空并没有形成大气波导层,因此,大气波导水平分布并不是均匀的, 只是出现在雷达站附近的平原地区,致使电磁波向下弯曲并超过地球曲率。
|
|
表 3 2005年11月21日08时北京、张家口、济南探空记录及大气修正折射模数计算结果 Table 3 The records and calculated results of atmospheric modified refractive modulus at Beijing, Zhangjiakou, and Jinan sounding stations |
根据2005年11月21日08时邢台探空资料计算的大气折射模数N和大气修正折射模数M, 结合图 4石家庄新一代天气雷达遮蔽角图和07:45雷达0.5°反射率因子产品的超折射回波实况, 我们利用球面大气分层的Snell定律,假设在球面分层的各层中电磁波波束直线传播,按照进入大气波导层之前、在大气波导层中以及出大气波导层底达到地面的三个层次对该时刻电磁波的传播路径进行分析。
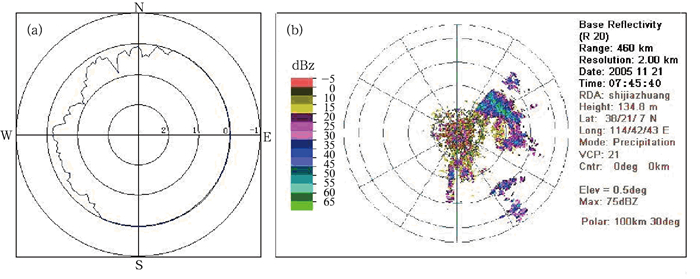
|
图 4 石家庄新一代天气雷达遮蔽角图(a)和2005年11月21日07:45:40石家庄CINRAD/SA雷达0.5°反射率因子产品超折射回波图(b) Fig. 4 The shield angle map (a) and superrefraction echoes on 0.5°reflectivity of Shijiazhuang CINRAD/SA radar (b) at 07:45:40 on November 21, 2005 |
由Snell公式可知[9]:
| $ \left( {r + H} \right)n\left( H \right)\cos \varphi \left( H \right) = {C_0} $ | (5) |
其中φ(H)为电磁波在H高度的仰角,n(H)是H高度上的折射率,r为地球半径,C0为Snell常数。
n(H)可用下述公式求出[9]:
| $ n\left( H \right) = \frac{{77.6}}{{T\left( H \right)}}\left[{p\left( H \right) + \frac{{4810e\left( H \right)}}{{T\left( H \right)}}} \right] \times {10^{ - 6}} + 1 $ | (6) |
T(H)、p(H)、e(H)分别是H高度上的气温、气压、和水汽压。
C0可用电磁波的初始入射角φ(H0),初始位置的海拔高度H0和所在高度n(H0)求出。
即:
| $ {C_0} = \left( {r + {H_0}} \right)n\left( {{H_0}} \right)\cos \varphi \left( {{H_0}} \right) $ | (7) |
则在波束传播过程中,各点的仰角为:
| $ \cos \varphi \left( H \right) = \frac{{{C_0}}}{{\left( {r + H} \right)n\left( H \right)}} $ | (8) |
当
石家庄新一代天气雷达的天线海拔高度为135 m,地面海拔高度为75 m,如果以邢台探空站海拔174 m以下的气压、温度、露点温度数据来近似雷达站天线所在高度的数值,雷达初始天线仰角按照0.5°,地球半径r=6.371×106m, 来计算n(H0)和C0。
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;n\left( {{H_0}} \right) = 1.00031927\\ {C_0} = \left( {6371000 + 135} \right) \times 1.00031927 \times \\ \;\;\;\;\;\;\;\;\;\cos {0.5^ \circ } \approx 6372926 \end{array} $ |
大气波导层的底部所在高度为270 m,根据探空资料,由式(6) 可求得:
| $ n\left( H \right) = 1.0003121 $ |
由公式(8) 可以计算出电磁波在大气波导层底部雷达的入射角约为:
| $ \begin{array}{l} \cos \varphi \left( H \right){\rm{ = }}\frac{{{C_0}}}{{\left( {r + H} \right)n\left( H \right)}}{\rm{ = }}\\ \;\;\;\frac{{6372926}}{{\left( {6371000{\rm{ + }}270} \right) \times 1.0003121}} \approx 0.999948\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\varphi \approx {0.585^ \circ } \end{array} $ |
可以算出,当初始入射角≤0.5°时, 总是保持C0<(r+H)n(H), 即cosφ(H)<1, 因此,电磁波在进入大气波导层前不会出现全反射。
3.1.2 大气波导层内石家庄新一代天气雷达的天线垂直波束宽度为0.91°, 因此波束轴线与底边半功率点的夹角为0.455°, 如果雷达电磁波在大气波导层底部的入射角为φ=0.585°,则雷达电磁波束底边的入射角约0.13°, 同样, 如果以波束底边的入射角、大气波导底层高度和大气折射率来计算n(H0)和C0,则:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;n\left( {{H_0}} \right){\rm{ = }}1.0003121\\ {C_0} = \left( {6371000{\rm{ + }}270} \right) \times 1.0003121 \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\cos \;{0.13^ \circ } \approx 6373242 \end{array} $ |
大气波导层的顶部所在高度为362 m,根据探空资料,由式(6) 可求得:
| $ n\left( H \right) = 1.00029487 $ |
由公式(8) 可以计算出电磁波到达大气波导层顶部雷达的入射角约为:
| $ \begin{array}{l} \;\;\;\;\;\;\cos \varphi \left( H \right)\frac{{{C_0}}}{{\left( {r + H} \right)n\left( H \right)}}\\ \frac{{6373242}}{{\left( {6371000 + 362} \right) \times 1.00029487}} > 1 \end{array} $ |
此时,上式无意义,满足全反射发生条件。可以算出,对于在大气波导底部初始入射角≤0.13°的电磁波, 在波导层顶部始终为C0≥(r+H)n(H), 即cosφ(H)≥1, 这说明,在大气波导层内,如果电磁波传播的初始入射角≤0.13°,电磁波在波导层内产生全反射。
3.2 计算各层的电磁波传播距离 3.2.1 在进入大气波导层之前波束传播距离在球面分层大气的每层中,假设波束直线传播。由探空资料,大气波导层的底部所在高度为270 m,根据天线仰角、高度和大气波导层底部高度,可以计算出电磁波在进入大气波导层之前的传播距离R1。
| $ {R_1} = \frac{{135}}{{\sin \left( {{{0.5}^ \circ }} \right)}} \approx 15469\;{\rm{m}} $ |
从遮蔽角图 4a可以看出,石家庄雷达站以方位30°至210°为分界线,东南侧为平原,西北侧为山区。由于在0.5°仰角受到西部山区遮挡,电磁波不能继续向前传播,在回波图 4b上,以山脉走向为分界,超折射回波主要分布在东部平原。
3.2.2 在大气波导层中电磁波传播距离根据前面计算,在大气波导层底部,雷达电磁波束底边的入射角约0.13°, 产生了全反射,由此可以计算出电磁波在波导层的自底部至顶部传播距离R2′。
| $ {{R'}_2} = \frac{{92}}{{\sin \left( {{{0.13}^ \circ }} \right)}} \approx 40546\;{\rm{m}} $ |
然后,电磁波反射回大气波导底层,则在大气波导层内的传播距离为:
| $ {R_2} = 2 \times {{R'}_2} \approx 81093\;{\rm{m}} $ |
在大气波导层传播距离约81 km。
3.2.3 穿出大气波导层底到达地面时的电磁波传播距离根据文献,高架雷达电磁波俯视探测时,对高度H为目标物的雷达最大探测距离为[9]:
| $ R = \sqrt {2 {{R'}_{\rm{m}}}} \left( {\sqrt H + \sqrt h } \right) $ | (9) |
| $ {R'_{\rm{m}}} = \frac{{{R_m}}}{{1 + {R_m}\frac{{{\rm{d}}n}}{{{\rm{d}}h}}}} $ | (10) |
式中H、h分别为目标物和天线架高的海拔高度,Rm′和Rm分别为等效地球半径和真实地球半径。对于标准大气:
| $ R = 4.15\left( {\sqrt H + \sqrt h } \right) $ | (11) |
当到达地面,即目标物高度H=0时:
| $ R = 4.15\left( {\sqrt h } \right) $ | (12) |
这里H、h以m为单位,R以km为单位,从前面对张家口、北京和济南探空站的资料分析可知,在距离雷达站较远的地区上空不存在大气波导层。因此,可以用上述公式来计算电磁波移出大气波导层到达地面的传播距离。如果平原地区的平均海拔高度按50 m计算, 大气波导层底部的海拔高度为270 m, 则此时电磁波到达地面时的传播距离约为:
| $ {R_3} = 4.15 \times \left( {\sqrt {270 - 50} } \right) \approx 61.554\;{\rm{km}} $ |
由大气波导层底到达地面时电磁波传播距离约62 km。
当电磁波以较小的负仰角穿过大气波导层向地面传播时,由于大气折射率分布不均匀和华北平原地形情况,大致可以出现以下三种情况:(1) 电磁波到达地面后继续传播,并且探测到平原远处的山脉。(2) 电磁波到达地面后返回,形成超折射回波。(3) 电磁波由于向下弯曲的曲率较小,没有到达地面,电磁波向前传播,直到探测到更远处的山脉。
因此,电磁波波束在进入大气波导层之前、在波导层中及自大气波导底到达地面三段所对应的沿地面传播的距离分别约为15 km、81 km和62 km,三者之和为158 km,即电磁波波传播的总距离R。
| $ R = {R_1} + {R_2} + {R_3} \approx 158\;{\rm{km}} $ |
这与图 4b中160 km左右开始出现较强回波是相吻合的。东北部300 km左右再次出现了较强的地物回波,这说明,电磁波接近地面后继续向东北方向传播,遇到了山脉或到达地面。
从上面对2005年11月21日08时的探空资料和雷达回波的分析可以看出,由于雷达站附近在270~362 m出现了
文献[5-6, 10]指出,华北平原形成大雾的主要原因是大气层结稳定,水汽充沛,逆温层的高度和强度影响雾的形成,深厚逆温层的维持对雾层长时间维持起着决定性作用。当近地面水平风很弱, 相对湿度为80%~90%,温度露点差在2~4℃,饱和湿空气气层处于稳定或者弱不稳定状态,以及近地面气温在3~9℃时,华北平原雾的发生频率较高。
从前面对超折射回波的气象条件和探空资料的分析可以看出,在雾的顶部温度场出现较强逆温层, 相对湿度递减梯度加大,
表 4是2004-2007年华北平原出现的10次大雾天气过程中超折射回波出现的时间分布,可以看出每次大雾天气过程均有超折射回波出现。超折射回波还具有明显的日变化,10次大雾天气过程超折射回波多出现在夜晚和上午, 而在午后则出现较少。此外,从强度变化来看,超折射回波一般傍晚以后开始强度增强, 夜间和清晨强度达到最强。
|
|
表 4 10次大雾天气过程中超折射回波的时间分布 Table 4 The time distributions of superrefraction echoes in 10 dense fog weather events |
由于目前每天仅有08:00和20:00两次探空资料,因此对雾的观测和分析受到很大限制。CINRAD/SA型多普勒天气雷达每6分钟进行一次体积扫描,探测资料的连续性很强,24小时连续运行,能够提供回波强度、径向速度等参数的空间分布。多普勒天气的超折射回波能够反映出边界层内温度、湿度等气象要素的垂直分布情况,超折射回波的存在表明逆温层的存在和低层水汽含量较高,大气层结稳定。从华北平原出现的10次大雾天气过程中的多普勒天气雷达超折射回波出现的时间分布来看, 超折射回波主要出现在大雾天气的维持和发展阶段。
5 结语通过对超折射回波的射线追踪分析和气象条件的讨论,可以看出,在华北平原大雾天气出现时, 在雾的顶部存在
姚展予, 赵柏林, 李万彪, 等, 2000. 大气波导特征分析及其对电磁波传播的影响[J]. 气象学报, 58(5): 605-616. DOI:10.11676/qxxb2000.062 |
胡晓华, 费建芳, 张翔, 等, 2007. 气象条件对大气波导的影响[J]. 气象科学, 27(3): 349-354. |
浙江金华地区气象台雷达组, 1979. 超折射回波与未来降水[J]. 气象, 5(12): 32-33. DOI:10.7519/j.issn.1000-0526.1979.12.015 |
官莉, 顾松山, 火焰, 等, 2003. 大气波导形成条件及传播路径模拟[J]. 南京气象学院学报, 26(5): 631-637. |
毛冬艳, 杨贵名, 2006. 华北平原雾发生的气象条件[J]. 气象, 32(1): 78-83. DOI:10.7519/j.issn.1000-0526.2006.01.013 |
康志明, 尤红, 郭文华, 等, 2005. 2004年冬季华北平原持续大雾天气的诊断分析[J]. 气象, 31(12): 51-56. DOI:10.7519/j.issn.1000-0526.2005.12.010 |
田华, 王亚伟, 2008. 京津塘高速公路雾气候特征与气象条件分析[J]. 气象, 34(1): 66-71. DOI:10.7519/j.issn.1000-0526.2008.01.010 |
张宗灏, 王咏青, 2007. 鲁西南雾的统计特征[J]. 气象, 33(11): 82-86. DOI:10.7519/j.issn.1000-0526.2007.11.013 |
张培昌, 杜秉玉, 戴铁丕, 2001. 雷达气象学[M]. 北京: 气象出版社, 94, 308, 334-121, 310, 335.
|
董剑希, 雷恒池, 胡朝霞, 等, 2006. 北京及其周边地区一次大雾的数值模拟及诊断分析[J]. 气候与环境研究, 11(2): 175-184. |
 2010, Vol. 36
2010, Vol. 36 