2. 山西水利职业技术学院,运城 030014;
3. 山西省运城市水利科学研究所,运城 030014
2. Shanxi Technical College of Water Conservancy, Yuncheng 030014;
3. Yuncheng Water Conservancy Research Institute of Shanxi, Yuncheng 030014
农田土壤水分是影响作物生长及产量的重要环境因子,也是分析研究农田水循环的一个重要因素。特别是在农业灌溉用水不足的条件下,准确掌握农田土壤水分变化动态,有助于合理确定作物的灌水时间,提高有限灌溉供水量的利用效率。
农田土壤水分变化动态的分析研究,一直是农业和水利学者们关心的一个重要问题。对此人们已提出了多种分析方法,建立了不同类型的土壤水分变化模拟模型。其中土壤水动力学模型具有严格的理论基础[1],能够给出农田土壤剖面含水量的时空变化特征,是进行土壤水分蒸发、入渗、土壤溶质运移等农田物质能量转化研究的基本依据。但是,在通常情况下人们更多地关心根区或称为根系层土壤水分平均值的变化,为此,许多学者致力于农田土壤水分变化概念性模型的研究[2-8],并由此为水文循环等研究提供依据[9]。本文以山西水利职业技术学院试验基地2007年和2008年冬小麦试验资料分析建立了麦田土壤水分变化模拟模型。
1 模型描述模型以作物根区土体为研究对象,依据水量平衡方程分析作物蒸散、降水、灌水、深层土壤水分补给以及深层渗漏等对土壤水分变化动态的影响。田间土壤水分变化动态模拟模型主要由作物蒸散模型、根区下界面水分通量模型和根区土壤水量平衡方程组成。
1.1 根区水量平衡方程根区水量包括时段内进入根区的降水量、灌水量、通过根区下界面向根区补给的水量、时段初土壤的储水量、地表径流量,时段内流出根区的水量,包括作物蒸散量、通过根区下界面流出根区的水量、地表径流量以及时段末土壤储水量等,在农田条件下,地表径流量一般较小,常忽略不计。
时段[t0,t1]内根区土体单元水量平衡方程如下,
| ${{W}_{1}}-{{W}_{0}}=\sum P+\sum IR-\int_{{{t}_{0}}}^{{{t}_{1}}}{{}}ET\text{d}t-\int_{{{t}_{0}}}^{{{t}_{1}}}{{}}q\text{d}t$ | (1) |
式中:W0为时段初(t0)的土壤储水量,单位:mm;W1为时段末(t1)的土壤储水量,单位:mm;∑P为时段内的降水量,单位:mm;∑IR为时段内的灌水量,单位:mm;ET为作物蒸散量,单位:mm·d-1;q为根区下界面水分通量,向下为正,单位:mm·d-1。
1.2 作物蒸散模型作物蒸散量是指作物叶面蒸腾和棵间土壤蒸发量之和。由于田间条件下作物蒸腾和蒸发难以区分,因而常将两者合并计算,称为作物蒸散量。依据根区土壤水分大小可将作物蒸散的计算分为两种情况,一种是充分供水条件下的作物蒸散量的计算,一种是非充分供水条件下的作物蒸散量的计算。用分段函数表示如下[4],
| $ET=\left\{ \begin{array}{*{35}{l}} {{K}_{c}}\cdot E{{T}_{0}}~ & \theta \ge {{\theta }_{j}} \\ {{K}_{\theta }}\cdot {{K}_{c}}\cdot E{{T}_{0}} & {{\theta }_{wp}}\le \theta <{{\theta }_{j}} \\ \end{array} \right.$ | (2) |
式中:ET为作物蒸散量,单位:mm·d-1;ET0为参考作物蒸散量,单位:mm·d-1;Kc为作物系数;Kθ为土壤水分修正系数。其中参考作物蒸散采用FAO 1998年推荐的FAO Penman-Menteith公式[2]计算,
| $E{{T}_{0}}=\frac{0.408\Delta ({{R}_{n}}-G)+\gamma \frac{900}{T+273}{{u}_{2}}({{e}_{s}}-{{e}_{a}})}{\Delta +\gamma (1+0.34{{u}_{2}})}$ | (3) |
式中:Rn为作物冠层顶的净辐射,单位:MJ·m-2·d-1;G为土壤热流强度,单位:MJ·m-2·d-1;T为2 m高度处的日平均气温,单位:℃;u2为2 m高度处的风速,单位:m·s-1;γ为湿度计常数,单位:kPa·℃-1;Δ为饱和水汽压—温度曲线斜率,单位:kPa·℃-1;es为气温为T时的饱和蒸汽压,单位:kPa;ea为气温为T时的实际蒸汽压,单位:kPa;其余符号意义同前。
土壤水分修正系数是根区土壤水分的函数,可用下式计算[1],
| ${{K}_{\theta }}=\text{ }\left\{ \begin{array}{*{35}{l}} 1\text{ } & {{\theta }_{j}}\le \theta \\ {{\left( \frac{\theta -{{\theta }_{wp}}}{{{\theta }_{j}}-{{\theta }_{wp}}} \right)}^{n}}~ & {{\theta }_{wp}}\le \theta <{{\theta }_{j}} \\ 0 & \theta <{{\theta }_{wp}} \\ \end{array} \right.$ | (4) |
式中:θ为作物根区实际含水率,单位:%(以体积含水率表示,下同);θwp为土壤凋萎点含水率,单位:%;θj为蒸散开始受土壤含水量影响时的临界含水量,单位:%,令θj=Bjθf,θf为作物根区最大田间持水率,单位:%;Bj为与θj相对应的系数;n为经验指数,由实测资料分析求得。
作物系数反应了作物生长特性对蒸散的影响,随生育阶段不同而变化。参照FAO推荐的分段单值平均作物系数法及其相应的阶段划分方法,将冬小麦生育期划分为初始生长期、快速发育期、生育中期、成熟期等四个时期[5],其中初始生长期包括了苗期、冬前分蘖期和冻融期等三个时期。对快速发育期和成熟期作物系数的变化采用曲线表示,其他两个时期用常数表示。据此本文给出全生育期作物系数的变化过程表达式,
| ${K_c} = \left\{ {\matrix{ {{K_{c\min }}} \hfill & {0 \le {t_1}} \hfill \cr {{a_0} + {a_1}t + {a_2}{t^2} + {a_3}{t^3}} \hfill & {{t_1} \le t < {t_2}} \hfill \cr \matrix{ {K_{c\max }} \hfill \cr {b_0} + {b_1}t + {b_2}{t^2} \hfill \cr} \hfill & \matrix{ {t_2} \le t < {t_3} \hfill \cr {t_3} \le t \le {t_4} \hfill \cr} \hfill \cr } } \right.$ | (5) |
式中Kcmin为初始生长期的作物系数;Kcmax为生育中期的作物系数;t1,t2,t3,t4为与作物系数变化相对应的累积天数,其中t4为全生育期生长天数;a0, a1, a2, a3, b0, b1, b2为模型参数,其中a0, a1, a2, a3和b0, b1, b2中的6个参数可利用作物生长连续性的特点由其他参数求得。
根据作物生长的连续性,在t=t1, t2, t3处,作物系数分别为Kcmin, Kcmax和Kcmax,且作物系数的曲线应该是光滑的,亦即,三点处的导数应该等于零,
| ${{a}_{3}}=\frac{{{K}_{c\max }}-{{K}_{c\min }}}{t_{2}^{3}-t_{1}^{3}+3{{t}_{1}}{{t}_{2}}({{t}_{2}}-{{t}_{1}})-1.5({{t}_{2}}-{{t}_{1}}){{({{t}_{2}}+{{t}_{1}})}^{2}}}$ | (6) |
| ${{a}_{2}}=-1.5{{a}_{3}}({{t}_{2}}+{{t}_{1}})$ | (7) |
| ${{a}_{1}}=3{{t}_{1}}{{t}_{2}}{{a}_{3}}$ | (8) |
| ${{a}_{0}}={{K}_{c\max }}-{{a}_{3}}{{t}_{2}}^{3}-{{a}_{2}}{{t}_{2}}^{2}-{{a}_{1}}{{t}_{2}}$ | (9) |
| ${{b}_{0}}={{K}_{c\max }}+{{b}_{2}}{{t}_{3}}^{2}$ | (10) |
| ${{b}_{1}}=-2{{b}_{2}}{{t}_{3}}$ | (11) |
由此可见,参数a0, a1, a2, a3和b0, b1可由参数Kcmin, Kcmax, t1, t2, t3, b2确定。从而减少待定参数的个数。其中t1, t2, t3根据FAO阶段划分方法确定,对本试区t1=140,t2=200,t3=225 d。因而,作物系数模型的待定参数只有Kcmin, Kcmax和b2 3个。
1.3 根区下界面水分通量模型根区下界面水分通量是单位时间通过根区下界面单位面积向上或向下运移的土壤水量。可用下式表示[6, 8]
| $q=a{{\left( \frac{W}{{{W}_{f}}} \right)}^{d}}(W-{{W}_{c}})$ | (12) |
式中:a,d为待定参数;W为根区土壤储水量,单位:mm;Wf为根区土壤田间持水量,单位:mm;Wc为根区临界土壤储水量,单位:mm;其中W=10γHθ,Wf=10γHθf,Wc=10γHθc,θ, θf和θc分别为与W, Wf和Wc相对应的土壤体积含水率,单位:%;H为根区深度,单位:m。本文研究中取H=1 m。
根区临界储水量Wc是估算根区下界面水分通量的一个重要参数,由式(12) 可见,当根区土壤储水量W大于临界储水量Wc时,根区下界面水分通量方向向下,当根区土壤储水量小于临界储水量时,根区下界面水分通量方向向上,当W=Wc时,通量为零。临界储水量Wc主要与地下水埋深有关,理论上,可利用土壤水分特征曲线确定临界储水量与地下水埋深的关系,
| ${{W}_{c}}={{a}_{c}}L_{w}^{{{b}_{c}}}$ | (13) |
式中,Wc的单位为mm,地下水埋深Lw单位为m,ac, bc为待定参数。考虑本试区土壤质地,取ac=385.11, bc=-0.172[5]。若地下水埋深较深(Lw>5),Wc可取为常数。
2 材料与方法 2.1 模型参数辨识方法采用最小二乘法进行参数辨识。设选择一组土壤水分观测值[W11,W21],W11和W21分别为某一时段[t1,t2]初和末的土壤储水量,假定一组参数,用式(1) 至式(13) 从时段初开始逐日计算,直到计算出时段末的土壤储水量
| $SS=\min \sum\limits_{i=1}^{m}{{}}{{({{{\hat{W}}}_{2i}}-{{W}_{2i}})}^{2}}$ | (14) |
式中:i为时段编号,下脚标2表示时段末,即W2i和2i为第i个时段实测的土壤储水量和计算的土壤储水量;m为时段总数。根据最小二乘法原理,参数优选目标是使实测的土壤储水量与模型计算的土壤储水量误差最小。由于式(14) 的非线性特性,参数优选不能采用解析法,必须采用非线性优化方法。本文采用坐标轮换法[10]及Excel软件提供的规划求解工具进行参数优化。
2.2 资料及其测试方法试验区位于山西省南部的运城市盐湖区,34°48′27″°N、110°41′23″°E,海拔370 m。年平均降雨量559.3 mm,年平均日照时数2247.4 h,年平均气温13.6 ℃,全年无霜期208 d左右。试验区土壤属于中壤土,土壤有机质为10.39 g·kg-1,全氮量为0.5 g·kg-1,全磷为0.5 g·kg-1。0~100 cm和100~160 cm土层的土壤容重均为1.45 g·cm-3,田间持水率为22%(占干土重的%), 地下水埋深大于6 m。
试验作物为冬小麦,设置4个小区试验处理,见表 1处理1至处理4。每个处理设3个重复,且3个重复相邻布置,小区面积66 m2,小区之间不设隔离区,整个试区周边须设置保护区。同时设置3个大田对照处理,见表 1处理5至处理7。采用畦灌,畦幅规格:3.3 m×20 m=66 m2。管道输水灌溉,水表量水。
|
|
表 1 试验处理设计 Table 1 Design of experiments |
用中子仪测试土壤水分,从地表开始,每20 cm一层,直到160 cm。测试时间为播种、收获、灌水前后,以及重要的生育期等。2006—2007年和2007—2008年二个年度试验期间共测试土壤含水率117次。其中2007年度于2006年10月11日播种,于2007年5月28日收获;2008年度试验于2007年10月16日播种,于2008年5月29日收获,两个年度均采用邯郸6172品种。施肥水平同当地农户。实际灌水时间,2007年度冬水为1月18日,拔节水为3月23日,抽穗水为4月22日,灌浆水5月5日;2008年度冬水为12月20日,拔节水为3月28日,抽穗水为4月22日,灌浆水5月6日。
3 结果分析 3.1 待定参数初始值的确定及参数优化结果由式(1) ~(13) 可知,麦田土壤水分动态模拟模型的待定参数有14个,其中需要优化确定的参数有8个(表 2)。待定参数a, d, Wc, n, Bj初始值的确定参照王仰仁等的研究[6],Kcmin, Kcmax, t1, t2, t3的确定参照段爱旺等的研究[5],结果见表 2。对于根区临界储水量Wc,由于地下水埋深较大,在参数优选过程中取为常数,参照式(12),初始值取385×6-0.172=282 mm。在灌溉条件下,冬小麦根区深度取1 m。参数优选结果见表 2。由式(5) ~(10) 可求得a0=27.4717,a1=-0.5012,a2=3.04×10-3,a3=-5.97×10-6,b0=-12.0973,b1=0.1184。
|
|
表 2 冬小麦田间水分转化模型参数优选结果 Table 2 Model parameters of field soil water transformation for winter wheat |
采用标准误差(σ)、复相关系数(R)和模拟计算值与实测值散点图(图 1)对拟合精度进行评价,采用F检验法对拟合模型进行检验,相应的计算公式见式(15) ~(16),其计算结果见表 2。由表 2可见土壤储水量模拟计算值与实测值的复相关系数R达到0.9555,F=139.56>F0.001=3.55,表示模拟值与实测值有较好的一致性,所建立的麦田土壤水分动态模拟模型达到极显著水平,可用于麦田土壤水分变化动态的模拟计算。其标准误差为11.87 mm,占土壤储水量的3%~11%。
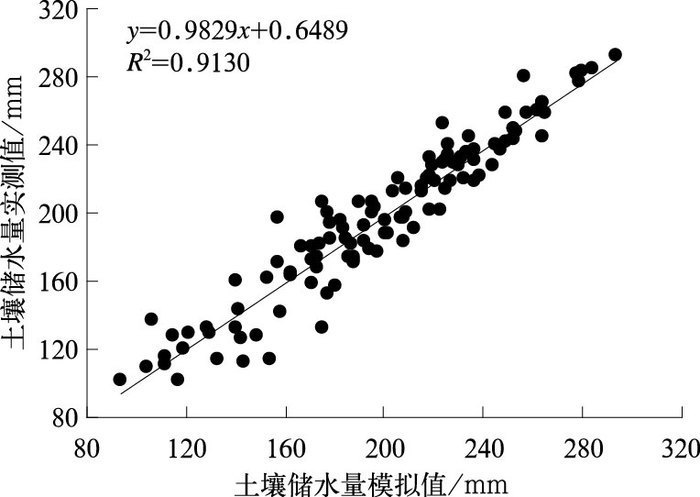
|
图 1 冬小麦根区土壤储水量模拟计算值与实测值比较散点图 Fig. 1 Relationship between measured and simulated soil moisture storage of root zone for winter wheat |
| $\sigma =\sqrt{\frac{SS}{m-p-1}}$ | (15) |
| ${{R}^{2}}=1-\frac{SS}{ST}$ | (16) |
式中ST为总平方和,
由图 1可见,(1) 模拟计算值与实测值拟合直线非常接近于通过原点的45°直线,表明参数优选结果是较好的;(2) 但是,在土壤储水量较小时拟合误差相对较大,其原因有待进一步研究。
3.3 独立样本精度检验为了检验上述模型及其参数的合理性,图 2给出了本试区同期大田试验(试验小区面积为334 m2)处理土壤水分模拟值和实测值比较的散点图。由图 2可见,大田试验处理模拟计算的土壤储水量与实测的土壤储水量非常接近。但是,在土壤含水量较小时预测误差较大,其原因有待进一步研究。
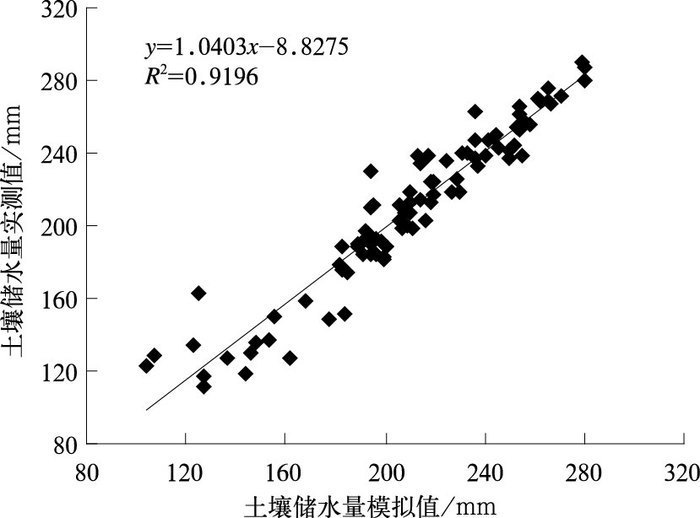
|
图 2 大田试验冬小麦根区土壤储水量模拟值与实测值比较散点图 Fig. 2 Relationship between measured and simulated soil moisture storage of root zone for winter wheat under field scale experiment |
图 3以2008年度试验中中等灌水(处理1) 和不灌水(处理4) 为例,给出了冬小麦全生育期土壤水分修正系数随时间的变化过程。由图可见,(1) 灌水处理的土壤水分较高,土壤水分修正系数保持了较大值,不灌水的处理则呈现持续减小的趋势,表明作物生长处于水分胁迫状态;(2) 在同样灌水定额条件下,前期灌水可维持较长时间使得土壤水分修正系数等于1,后期则维持时间较短,主要原因是冬小麦前期耗水强度较小,后期耗水强度较大,表明后期灌水时间间隔不宜过长,以保证作物尽可能少地遭受水分胁迫。

|
图 3 2008年度灌水3次和灌水0次处理土壤水分修正系数变化过程 Fig. 3 Variation of modified coefficient of soil moisture between 3 irrigation times and no irrigation in 2008 |
图 4仍以2008年度试验中中等灌水(处理1) 和不灌水(处理4) 为例,给出了冬小麦全生育期根区下界面水分通量随时间的变化过程。由图可见,(1) 不灌水处理除初期因土壤水分较高产生向下的水分通量外,整个生育期根区下界面水分通量均为负值,表明有深层水分向根区补给;(2) 对于灌水处理,尽管3次灌水的灌水定额相同,但是只在第一次灌水和第二次灌水后出现了两次向下的水分运移过程,第一次水分运移过程由2007年12月21日(灌水后)开始,一直持续到2008年1月9日,其中最大的水分通量达到13 mm·d-1,累计向下运移的水量达31.0 mm;第二次水分运移过程由2008年3月29日开始,到2008年4月2日结束,其中最大的水分通量达到1.62 mm·d-1,累计向下运移的水量达3.3 mm;第3次灌水,不仅没有产生向下的水分通量,而且增大了向上的水分通量(由灌水前的0.012 mm·d-1增大到0.292 mm·d-1)。主要原因是3次灌水前的土壤储水量(从前到后依次为228 mm、207 mm、166 mm)不同。由此可见,依据土壤水分选择合适的灌水时间,可显著减小向深层运移的水量,提高用水效率;(3) 在冬小麦生长期,除因灌水会造成短时间向下的水分运移过程外,绝大部分时间的根区下界面水分通量均呈现向上的运移过程,主要原因是冬小麦生长期降水量小,耗水强度大。
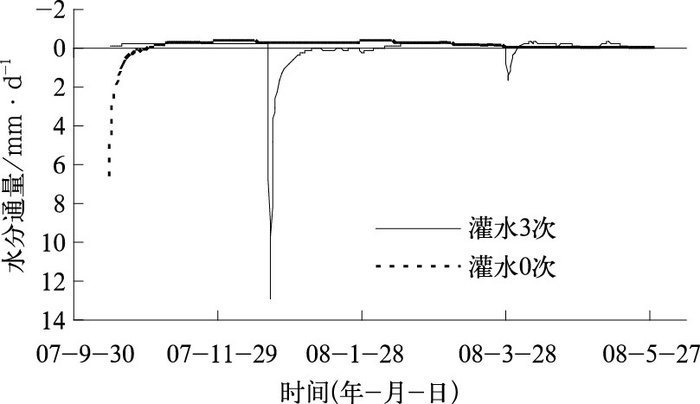
|
图 4 2008年度灌水3次和灌水0次处理根区下界面水分通量变化过程 Fig. 4 Variation of water flux through bottom of root zone between 3 irrigation times and no irrigation in 2008 |
表 3是2个年度冬小麦全生育期田间水分转化结果和产量。其中产量、灌水量和播前土壤含水率为实测值,蒸散量和水分通量为模拟计算值。分析计算表明,2个年度冬小麦生长期降水量非常接近,2007年度为102 mm,2008年度为106 mm;参考作物的蒸散量有一定差异,其中2007年度为588 mm,2008年度为565 mm。由表 3可见,(1) 在同等供水条件下,2007年度冬小麦蒸散量均小于2008年度的值,其中一个重要原因是2007年度播种时的土壤含水率较低,相应的产量也较低。表明播前土壤含水量对作物产量和蒸散量有较大影响;(2) 二个年度均有向上的根区下界面水分通量,且2008年度的值大于2007年度,主要原因是2008年度深层土壤含水量较大,播种时100~160 cm土层的含水率较2007年度平均高6.0%。
|
|
表 3 冬小麦田间水分转化及其与产量的关系 Table 3 Field water transformation and its relationship with yield for winter wheat |
作物产量与全生育期蒸散量有非常好的一致性(见表 3),即产量随蒸散量的增加而增大。图 5是以相对值给出的相对产量与相对蒸散量关系,其中纵坐标相对产量是以年度内最大产量为分母,横坐标以相应的最大蒸散量做分母求得相对蒸散量。由图可见,相对产量与相对蒸散量呈现二次抛物线关系,其复相关系数(R2)到达0.9972。表明模拟计算的蒸散量能够较好地反映水分对作物产量的影响。

|
图 5 产量与作物蒸散量的关系 Fig. 5 Relationship between evapo-transpiration and yield for winter wheat |
(1) 土壤储水量模拟计算值与实测值有较好的一致性,拟合精度和预测精度均较高,其模拟计算值和实测值的相关系数达到0.95以上,所建立的麦田土壤水分变化模拟模型可用于田间土壤水分的模拟计算,计算精度平均可达到3%~11%;
(2) 该模型较好地反映了农田土壤水分转化过程,以及降水、蒸发和深层土壤水分对作物蒸散及产量的影响;
(3) 模拟计算的蒸散量能够较好地反映水分对作物产量的影响。
雷志栋, 杨诗秀, 谢森传, 1988. 土壤水动力学[M]. 北京: 清华大学出版社, 282-303.
|
Allen R G, Pereira L S, Raes D, et al, 1998. Crop evapotranspiration guidelines for computing water requirements[J]. FAO Irrigation and Drainage Paper 56: 161-173. |
祝新建, 王新红, 张红卫, 等, 2009. 河南省获嘉县农田水分供需特征及秸秆覆盖效果分析[J]. 气象, 35(9): 98-103. DOI:10.7519/j.issn.1000-0526.2009.09.013 |
康绍忠, 刘晓明, 熊运章, 1994. 土壤-植物-大气连续体水分传输理论及其应用[M]. 北京: 水利电力出版社, 131-137.
|
段爱旺, 孙景生, 刘钰, 等, 2004. 北方地区主要农作物灌溉用水定额[M]. 北京: 中国农业科学技术出版社, 52-80.
|
王仰仁, 孙小平, 2003. 供水不足条件下作物蒸散量的计算[A].山西农业节水理论与作物高效用水模[M]. 北京: 中国科学技术出版社, 65-95.
|
王仰仁, 孙书洪, 叶澜涛, 等, 2009. 农田土壤水分二区模型的研究[J]. 水利学报, 40(8): 904-909. |
尚松浩, 毛晓敏, 雷志栋, 2009. 土壤水分动态模拟模型及其应用[M]. 北京: 科学出版社, 24-38.
|
夏智宏, 周月华, 许红梅, 2009. 基于SWAT模型的汉江流域径流模拟[J]. 气象, 35(9): 59-67. DOI:10.7519/j.issn.1000-0526.2009.09.008 |
尚松浩, 2006. 水资源系统分析方法及应用[M]. 北京: 清华大学出版社, 80-88.
|
 2010, Vol. 36
2010, Vol. 36 