引言

基于大气系统的非线性和复杂性, 加上初值和模式等自身无法避免的一些不确性^[1-4], 天气预报从单一值的决定论向多值的概率论转变不但符合气象科学的实际，也是更好地服务社会大众之必需^[5-6]。在本文的姐妹篇^[7]，我们已经谈了在这一转变中扮演中心角色的集合预报技术。不同于传统的统计办法，集合预报是用动力学的手段定量地把每个个体预报(不是平均情况)相对应的、特定的预报不确定性给度量出来。但如何来表达不确定性这是集合预报研究中的重要子课题^[8]，是目前国内外数值预报研究和业务预报的重要方法^[9-14]。概率是其中一个较常用的，也被大部分人所熟知的手段^[15]。虽然如此，但许多人仍对概率预报的真正含义不很清楚，对如何来衡量概率预报的优劣可能更是模糊。因此本文首先讨论了一下概率预报的含义及其相应的检验方法。

正如Alan Murphy^[16]所指出，任何一个预报只有当被用户充分理解并付之于决策行动之中，才有其真正的价值。否则，哪怕是一个100%准确的预报也没有任何价值。所以，本文接着讨论了如何应用概率信息来作决策的基本原则和方法。并用两个例子来说明，在承认预报有不可避免的误差即存在预报不确定性的前提下，应用概率预报其实比用单一值的决定论预报来决策更具经济价值。最后，用相对价值的概念从理论上来说明为什么概率预报一般比单一值确定预报更有应用价值。希望本文能帮助人们理解应用预报不确定性的价值。

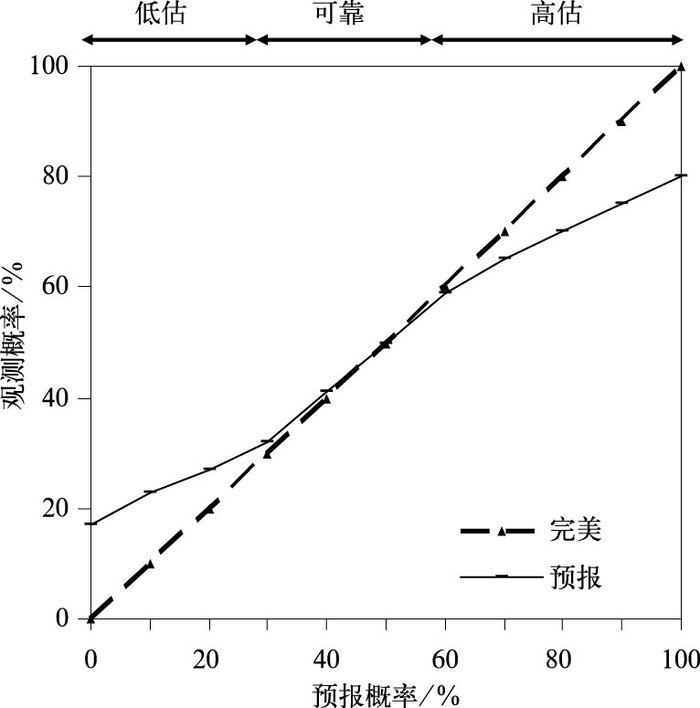
1 如何检验概率预报的准确性

不像单一值决定性预报，其黑白分明，从理论上来说它很容易被检验。但怎样来检验一个概率预报呢？譬如预报说60%会下雨，那么如果实况下雨了, 该说它是对的还是错的呢？其实, 对于某一个个例来说，我们既不能说它是对的也不能说它是错的。要检验概率预报，必须要有很多的个例，有了足够的样本数，才可以来检验一个概率预报是不是可靠(注意, 检验一个概率预报通常是说它是否“可靠”而不是说它是否“准确”)。一个完全可靠的概率预报, 譬如说60%。那么每100次“60%”的预报中，60次实况应该出现而40次不会出现，至于具体哪一次会出现哪一次不会出现则无从得知。这100次预报可以是时间上的(即在同一地点出现在不同时间上的100次同一概率预报)也可以是空间上的(即同一时间出现在100个不同地点上的同一概率预报)，当然也可以是时间和空间上混合的。概率预报的可靠与否通常用所谓的“可靠性曲线”来表征(如图 1)。当预报概率和观测概率(准确地说应该是频率, 因为概率是基于无限多的样本上的，而频率是基于有限的样本数上的)完全一致时(即预报完全可靠)其曲线就是对角线；当预报概率小于观测概率时(即低估或预报太保守)其曲线则位于对角线之上，当预报概率大于观测概率时(即高估或预报太自信)其曲线则位于对角线以下。图 1所示的是“0~30%”的预报过于保守(低估), “30%~60%”的预报基本可靠，而“60%~100%”的预报则太自信(高估)。

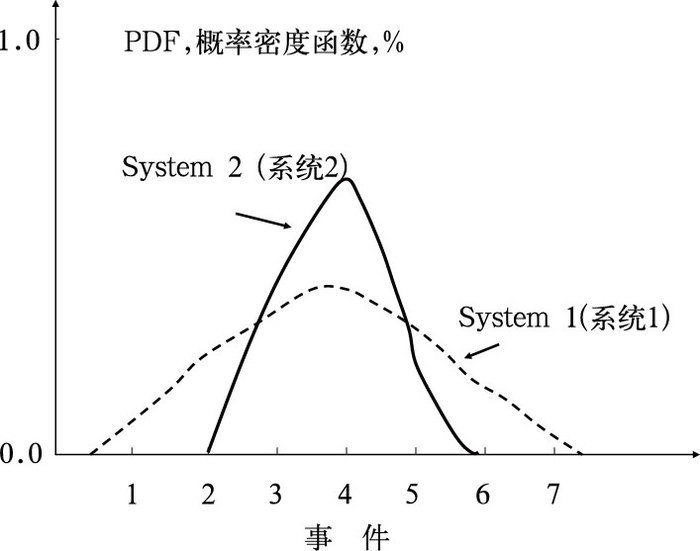
我们知道一个比较“尖窄”的概率分布(图 2中的实线)比一个“平宽”的概率分布(图 2中的虚线)含有更多的信息，因为它的不确定度较小，因而也有更高的应用价值。因此在保持概率预报的可靠性不变的前提下，这概率密度函数分布的尖窄或平宽也是衡量概率预报质量好坏的标志之一。例如，对一个有两种可能性(出现或者不出现)的事件，系统1的预报概率分布可能是(50%，50%)，而系统2的可能是(80%，20%)的分布。显然，系统2优于系统1，因为系统2比较确定。而相对于比较“尖窄”的概率分布，其对某一事件的预报也就较确定(譬如表 1的例子)。表 1列出了两个预报系统对5次气温的概率预报。假定每个预报系统所给出的概率预报对该系统本身来说是可靠的，那么预报系统B就优于预报系统A，因为从统计结果来看它对实况出现的事件的预报概率值(51%)一般大于预报系统A所提供的(42%), 因此也就更有可用的信息。通常，我们把一个预报概率分布同其相应的气候概率分布(它是完全可靠的, 因为它代表的就是实况)来相比较并称之为“分辨率”。如果它比气候概率分布还偏平的话，那么就没有分辨率可言, 因为它没有比仅仅用气候概率来作预报提供更多的信息和更有价值。只有比气候分布包含更多信息的概率预报才有分辨率、才有更大的价值。所以, 我们在追求概率预报的“可靠性”(不确定性的衡量)的同时也要追求它的高“分辨率”(确定性的衡量)。一般来说“可靠性”依赖于集合预报技术的好坏，而“分辨率”则依赖于模式和初值的质量。这儿我们又看到了文献[7]和[8]所强调的一个观点:即一个好的概率预报不仅仅决定于集合预报技术，同时也依赖于模式和初值的质量。所以, 我们在这两方面都不可偏倚。

从以前的讨论中知道(如文献[7]中的图 6), 集合预报的主要目的就是定量估计预报不确定性的大小。所以, 可预报性大的事件(容易报对, 其对应的观测概率也大)其不确定性就应该小，即预报概率大; 反之, 可预报性小的事件(不易报对，其观测概率也小)其不确定性就大，预报概率就小。所以一个基于集合预报系统上的概率预报的可靠与否也就是反映了该集合预报系统预报不确定性或反映大气可预报性能力的好坏。注意，因为预报概率的极大或极小其实都表明了事件具有较小的不确定性，所以为了防止误解，必须注意这儿所说的“可预报性”和“预报概率大小”所对应的事件是指在实况中出现了的事件，而不是指没有出现的反事件。譬如，某次“暴雨出现”的预报概率是80%，而另一次“暴雨出现”的预报概率为20%。如果实况是两次都出现了暴雨，那么我们则说前一次暴雨过程较后一次暴雨过程有较大的可预报性。然而，对于其反事件“没有暴雨”而言，其可预报性的结论则刚好相反，即如果两次实况都没有出现暴雨，那么对于“没有暴雨”事件而言，后一次的预报(80%不会出现暴雨)所对应的形势则比前一次的预报(20%不会出现暴雨)所对应的形势有较大的可预报性。这就是这儿所指的“可预报性”与“预报概率”成正比的含义。另外，需指出的是, 用统计的办法所产生的概率预报一般无法反映个别大气的可预报性，所以本文所说的概率预报一般都是指由集合预报产生的有动力学意义的概率预报。

2 如何应用概率预报来决策

很多人会问如果预报说50%会下雨，那么该如何来决策呢？是信“下雨”还是信“不下雨”呢？其实这一问题的答案取决于谁是用户，不同的用户会有截然不同的答案。对此问题过去已有一些研究^[17-21]。下面让我们来分析一下，表 2是预报和实际可能会出现的所有搭配情况以及决策和经济损失情况。实况出现并有预防措施时(即命中, HR), 经济损失有两部分:无法避免的财产损失(Lu)和采取措施的花费(C); 而无预防措施时(漏报, MR), 则有较大的财产损失L, L是Lu加上本可避免的财产损失(Lp)。当实况没有出现而采取了防范措施(空报, FAR)则有花费C; 而无防范措施(正确否决, CRR)则无任何经济损失和花费。这样当事件发生时，采取措施比不采取措施时可以减少的经济损失或说“利益”为(Lu+Lp)-(Lu+C)=Lp-C。但采取措施所面临的可能“风险”为C(如果实况不出现的话)。根据上面第1节的讨论, 对于一个完全可靠的概率预报P%而言，采取措施而获得“利益”的可能性为P%(实际会出现的可能性), 而承担“风险”的可能性为(100-P)% (实际不会出现的可能性)，即

$利益=(Lp-C) P\%$

(1)

$风险=C (100-P)\%$

(2)

有了这些定量的数据后，我们就可以按照经济的价值(即“利益/风险”比)来得到如下的决策模式：

$利益/风险比=\frac{\left( Lp-C \right)\text{ }P}{C\text{ }\left( 100-P \right)}\begin{matrix} >1采取措施 \\ =1中性 \\ ＜1不采取措施 \\ \end{matrix}\text{ }$

(3)

在式(3) 中, 0≤P≤100。

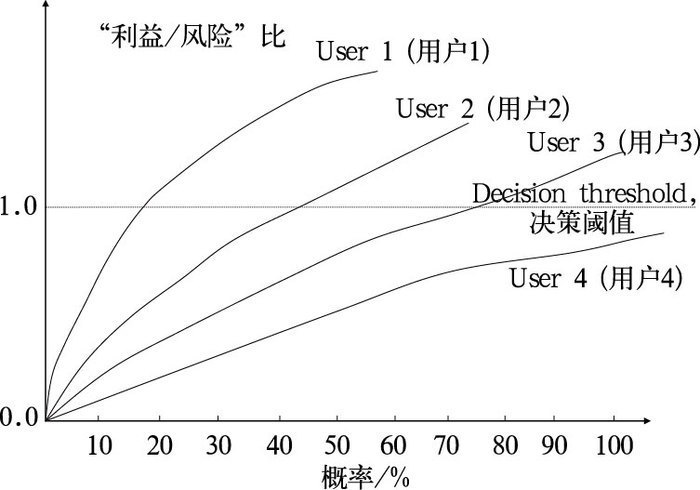
有了决策模式后, 概率P%就不再是“无意义”的数字了，而是对不同的用户而言有不同的实质决策含义(如图 3所示)。图 3表示用户1对气象条件依赖性较大(Lp$\gg $C)，当预报概率≥20%时就决定采取措施; 而用户3对气象条件依赖性较小，所以待概率≥80%时才采取行动; 用户2界于用户1和用户3之间，对气象条件依赖程度中等, 待概率≥50%时才采取行动；而用户4几乎不依赖于气象条件(C>Lp, Lp-C＜0)，所以在任何预报概率下都不采取措施，这类用户不在本文讨论之中。可见，概率预报同单一值的决定论预报的一个根本不同处就是用户现在可以根据自身对气象条件的依赖程度做出最佳的决策而不用再听任预报员的善意“摆布”了(在单一值决定论预报中，预报员实质上替所有的用户统一作了决策而使用户无选择余地)。从决策模式(3) 可以看到概率预报的“可靠性”很重要。如果预报概率不可靠，那么可能会导致决策的失误，所以集合预报系统的好坏是关键。

3 为什么概率预报比单一值决定论预报更有价值

在承认预报有不确定性、有误差的前提下^[1]，我们来举两个模拟的例子来说明多值的概率预报比单一值的决定论预报更有经济使用价值。假定结冰对某一工程的影响很大。如结冰, “可避免的损失”是Lp =800元，“不可避免的损失”Lu=200元，而采取措施的“费用”C=100元。所以“利益”是Lp-C=700元，其“风险”是C=100元。从“利益/风险”比为1 (公式3)，即700P=100(100-P)，可求得其“临界决策概率”为P%≈12.5%。假定有10次预报决策过程，表 3合理地比较了概率预报和单一值决定论预报所带来的经济损失(元)。可以想象, 单一值预报会有较多的“漏报”和“空报”; 而概率预报(尤其当临界决策概率较小时)一般不容易出现“漏报”, 但会有不少“空报”。这时利用概率预报来决策就会大大地减少经济损失。在这个例子中，损失减少了30%。所以, 如果气象部门能够提供可靠的概率预报，而所有的气象专业用户都能按照自己的行业决策模式来科学地、经济地决策，那将对整体国民经济的保值起巨大的作用。与气象有关的自然灾害每年对人的生命和财产带来很大的损失^[22-24]。据统计目前中国每年由于气象灾害所造成的经济损失至少达整个国家国民总产值的1%，所以哪怕只减少1%的损失就是一笔可观的数字!

下面再举一个稍为复杂一些的用户例子, 如利用风力发电。假如一个电力公司应用风的预报(可以转换为风能的预报)来计划调度电网中电源的分配。电力分配的主要任务是保证电的供与需的平衡，否则就会停电(如供不应求)或造成浪费(如供大于求)。我们知道利用风力发电的最大挑战是风的无常性，这使得风力发电的供电量经常随着时间变化。所以电力调度的计划，如备用方案的选择和准备等就特显其经济价值。有些方案的准备是需要提前安排的，如上游水库的放水到下游水库的发电可能有几天的时间差, 所以不提前采取行动是无法实施的。如果电力公司不知道风力预报的不确定性，那么他们只能假定预报是100%准确的，由此计算出来的风力发电也只能假定是对的，而无法事先估计它会错成什么样——是高估了还是低估了？如果高估了，会高估多少？如果低估了，又会低估多少？等等信息。所以也就无法事先实施备用方案(表 4a)，而只能待到实况出现时才没有选择余地的匆匆采取补救的应急措施:如发现实际发电量低于计划电量时, 只能到市场上临时用高价买电; 或相反，如实际发电量多于计划发电量时, 就只能匆匆减少其他发电源如水力发电而使水库泄洪而浪费大量的水资源等等。但是如果电力公司事先定量的预知预报的不确定性，知道有多少可能性计划发电被高估了或低估了, 这样他们就可以根据其出现概率的大小用上一节中所讨论的“利益/风险”比(公式3或图 3)的行业决策模式来预选和提前启用具最佳经济价值的备用方案以作好准备(如表 4b所示)。注意，表 4b所列的备案并不一定是真的反映实际情形中的最佳决策，这里只是作为一个模拟例子来说明。类似地，我们可以想象降水预报的不确性对于水资源的管理和利用也是具有巨大的经济价值的。从这些例子可以看到, 对有些用户而言他们如能预先知道气象预报的不确定性对他们的风险管理是非常重要的。并且, 随着中国经济的高速发展, 气象风险管理工作就会愈显重要。

下面我们再进一步从理论检验上来更普遍地说明这一点。如有人用“相对经济价值”的方法和概念显示了集合预报所产生的概率预报比单一值预报更有价值^[25-26]。这儿先来介绍一下如何衡量一个预报的价值。为了简化讨论和明确意义，假定表 2中Lu=0，即表示所有的损失都是可以避免的。假定某一特定的天气事件发生的气候概率为o，那么从平均来看如果你永远都不采取防范措施的话，根据表 2你的平均经济损失将是E_不防范=oL; 而相反，如果永远都采取保护措施的话，那么平均经济的损失(花费)是E_防范=C。所以，如果只用气候概率当作预报，用户的经济损失应该是

${{E}_{气候}}=\min \left\{ C,\bar{o}L \right\}$

(4)

即防范和不防范的决策取决于E_防范与E_不防范二者之中较小者。如果用户有一个100%准确的完美预报(注意：完美预报报“有”的概率同该事件实际发生的气候概率应是一样的), 那么他只在预报“有”时才防范，而“无”时不防范，这样平均的经济损失是

${{E}_{完美}}=\bar{o}C$

(5)

当然，实际预报并不完美，它有时对有时错。对于一个特定的预报系统而言，它的平均表现好坏是固定的，即表 2中的“命中率”HR，“空报率”FAR，“漏报率”MR, 和“正确否决率”CRR是已知的。这样对照表 2中的预报表现率和经济损失情况，对于一个不完美的单一值确定论预报其平均经济损失是

${{E}_{完美}}=HR×C+FAR×C+MR×L$

(6)

所以E_气候-E_预报就表示了一个实际预报系统相对于“仅仅用气候概率作预报”的价值。如果E_气候-E_预报＜0就表示没有任何价值，即还不如用气候概率当作预报为好。而E_气候-E_完美是一个预报系统有可能实现的最大价值。因此人们一般把一个预报系统的“相对经济价值”定义为

$V=\frac{{{E}_{气候}}-{{E}_{预报}}}{{{E}_{气候}}-{{E}_{完美}}}$

(7)

这样, 一个完美预报的V=1;只用气候概率作预报的V=0;只有当V>0时, 预报才比“仅仅用气候值作预报”更有意义。如果把式(4) ~式(6) 代入式(7) 的话，就得到

$\begin{align} & V=\frac{\min \left\{ C,\bar{o}L \right\}-HR\times C-FAR\times C-MR\times L}{\min \left\{ C,\bar{o}L \right\}-\bar{o}C} \\ & \quad =\frac{\min \left\{ \frac{C}{L},\bar{o} \right\}-HR\times \left( \frac{C}{L} \right)-FAR\times \left( \frac{C}{L} \right)-MR}{\min \left\{ \frac{C}{L},\bar{o} \right\}-\bar{o}\frac{C}{L}} \\ \end{align}$

(8)

如果注意到表 2中的HR+MR实际上就是某一事件实际发生的频率(即气候概率)o, 那么式(8) 可进一步改写为

$V=\frac{\min \left\{ \frac{C}{L},\bar{o} \right\}-HR\times \left( \frac{C}{L}-1 \right)\text{ }-FAR\times \left( \frac{C}{L} \right)-\bar{o}}{\min \left\{ \frac{C}{L},\bar{o} \right\}-\bar{o}\frac{C}{L}}$

(9)

式(9) 就是“相对经济价值”的通常表达方式。可见一个预报系统的相对价值同三方面有关:预报系统的好坏(命中率HR，空报率FAR), 所预报的对象(气候概率o, 即大概率事件还是小概率事件等), 以及用户对气象条件的依赖程度(“花费/损失”比C/L, 低风险用户C/L大，而高风险用户C/L小)。所以, 对于一个特定的预报系统如国家气象中心T213模式预报系统来说, 虽然预报同一天气现象如大风，那么对不同的用户有不一样的价值; 而对同一用户而言，对不同的天气现象其价值又不一样。既使对于同一用户和同一种天气现象，如果预报系统变化了，那其预报价值也就变了。甚至当改变某一预报系统时，对一部分用户而言可能变得更有价值了; 而对另一部分用户却可能变得有较小价值了。因此，天气预报对用户的价值是一个很复杂的关系，我们应该多进行这方面的评估和研究，多了解接触用户以提高天气预报的总体经济效益, 为更广泛的用户服务。而单看某一特定的预报检验指标是不够的, 而应该用一个综合性的衡量指标如类似UK-Index来评价，这样才会比较全面一些。

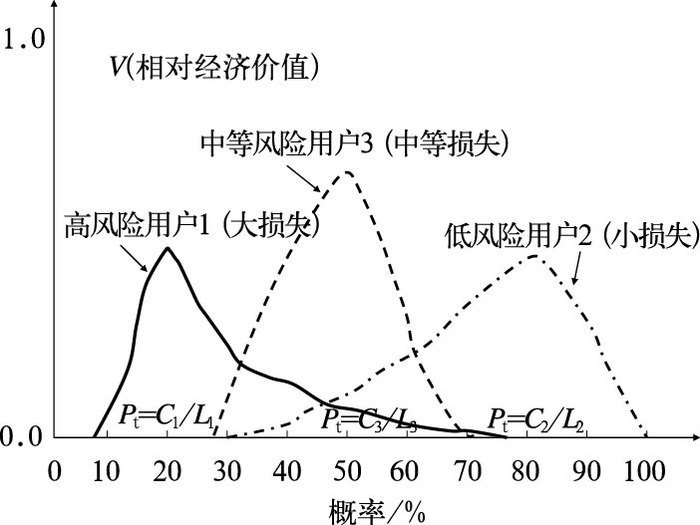
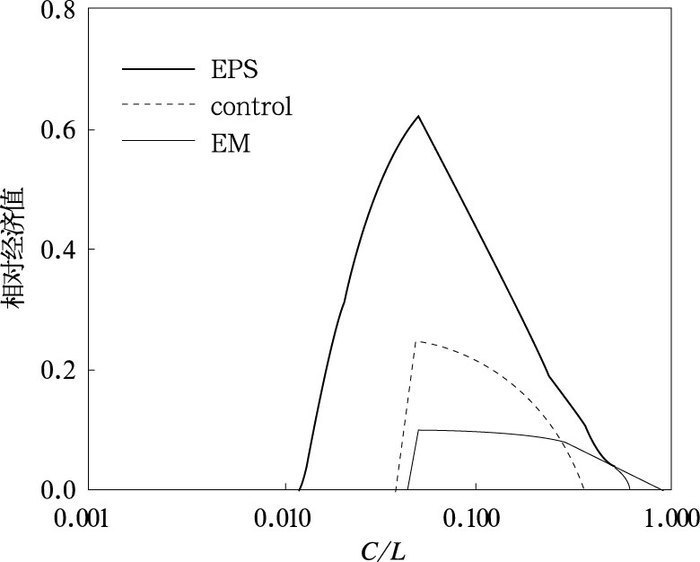
下面再回到单一值预报和概率预报的优劣问题上来。对于单一值确定论预报而言(如上面的二个例子), 它没有选择余地而只能听预报的，如果预报说“有”就防范, 否则就不防范。而对于概率预报, 不同的用户就可以根据自己独特的花费-损失比C/L来选择(变化)某一事件的预报概率值(从0%到100%)来作为自己的确定预报(从而HR和FAR就相应地变化)来看相对经济价值V的变化。当V达最大时的概率值就是最适合自己的临界决策概率P_t(图 4)。一般来说当概率P=C/L时, V达最大值(图 4)。譬如对高风险(潜在损失大)或低花费的用户(用户1) 其花费/损失比P_t=C₁/L₁较小，这样可能当概率P≥20%就当作“有”的预报; 而对低风险(潜在损失小)或高花费用户(用户2) 其花费/损失比P_t=C₂/L₂很大，可能当概率P≥80%才当作“有”的预报; 对中等风险用户(用户3)，其花费/损失比P_t=C₃/L₃居中, 待概率P≥50%当作“有”的预报。所以，同图 3类似，用户也是根据自己的“花费/损失”比C/L来计算最大的相对经济价值V来决策。对于一个来自同一预报系统、可靠的概率预报而言，这两种方法(图 3和图 4)应该是一致的，它们只是从不同的角度来表达。正是由于不同的用户可以根据自己特有的C/L在概率分布中来挑选最适合自己的预报以达到最大的价值，所以基于集合预报的概率预报一般比单一值预报更有经济价值。图 5是David Richardson根据欧洲中期数值天气预报中心(ECMWF)的集合降水预报所给出的检验结果^[25]。从该结果可以看到二点:第一, 由于上述所分析的原因，基于集合预报系统上的概率预报比单一值预报(控制预报和集合平均预报)更有价值(垂直轴，其曲线位于单一值预报的曲线之上)。第二，基于集合预报系统上的概率预报相对单一值预报而言对更多的用户群有价值(水平轴，其曲线比单一值预报包含更宽的C/L范围)。这是因为小概率预报对高风险或低花费的用户具有价值，但这些预报却因为概率值小而往往不被单一值预报选中而被仍掉。由此可见，单一值预报对某些用户有一定价值(但不一定达到最大的价值), 而对另外许多用户却没有用处。这儿又看到了我们在文献[7]中强调的观点:集合预报的主要目的是定量描述预报的不确定性、即给出预报的概率密度函数(分布)而不是给出一个更精确的单一值确定预报。因为即使一个更好更精确的预报也常常有误差，因而达不到最好的价值，且更重要的是满足不了广大的用户群特别是高风险的用户。这样就不能充分发挥集合预报的潜在优势。这儿顺便再讨论一下集合平均预报的价值。在图 5中我们看到一个有趣的现象，就是虽然集合平均预报(EM)相对控制预报而言对更多的用户(主要是低风险用户)有价值，但对不少风险比较高的用户而言其价值反而不如控制预报。出现这一似乎“反常”现象的原因是由于集合平均的光滑作用。这一光滑作用对降水预报尤其明显，如文献[27]指出集合平均会使“小雨”区扩大而使“大雨”区缩小。根据上面的讨论可推知，这种平滑了的预报(缺少了峰值)通常会使低风险的用户受益而使高风险的用户受损。

这样, 当气象用户认识到了天气预报有不可避免的不确定性^[1], 并了解了概率预报实际上比单一值预报更有经济价值时，他们就会科学地制定适合自己的概率决策指标如表 5。表 5表示了某行业对其行为有影响的天气事件种类及相关的临界决策概率。当一个行业有了适用于自己的类似表 5的决策指标以后，他们不但不会反对概率预报反而会主动地要求气象部门向其提供有关天气事件的概率预报。所以气象界需要向广大的用户进行广泛的科普宣传并同时跟他们深入合作。如何同各行各业合作建立科学的行业气象决策模式将是一项艰巨而有重要意义的工作。建议能有更多的优秀人才投身到这一创新的前沿阵地为社会作贡献。

虽然，上面用“花费-损失”比的经济模式可以说明并应用到许多实际情形中去，但在现实世界中并不是所有的情况都可以用数字来精确表达他们的价值。譬如人的生命就无法这样计算(除非把它当作无穷大的损失，这样无论多么小的概率都被当作是“有“的预报), 以及有些人为制定的操作规则等。所以在这些情况下，就要做些变通来运用上述的原理。另外，也可用其他不同的方法来利用概率预报的信息。从上分析知道，由于用户的决策风险不一样，对预报的要求就不一样。对于高风险的专业用户，定量的概率分布非常重要，既使是位于概率分布两尾端的小概率事件也极具重大的经济价值。但对于风险小的用户和一般日常生活起居所需的广大民众，他们也许不需要非常精确的概率数字，而只需了解预报不确定性的分级或分类的语言或文字表达, 如最大的可能性是A，同时也有较小的可能性会出现B等。电视天气预报也可用不同的颜色如红色、橙色、黄色、绿色、兰色或图画等来表达预报的不确定性等级。电视气象播报员也可用语调和动作来表达预报的不确定性。如何简单易懂而有效地来表达预报的不确定性这需要进行大量的社会调查并同有关的社会科学工作者合作一起来制定。对于上级领导, 可以坐下来面对面地向他们分析讲解预报的结果有哪几种可能性以及各种可能性的大小程度如何、并作出最好的决策(如最有可能的方案和备用方案是什么等等)。总之，对于不同的用户，要用最佳的不同方法来表达天气预报的不确定性以达到最佳的服务效果。

4 总结

本文试图用浅显易懂和举例的表达方式谈谈从单一值决定论预报向多值的概率预报转变的价值。这包括如何检验一个概率预报的好坏，如何使用概率预报来决策和为什么概率预报在实现世界中比单一值预报更有价值等。我们谈到一个好的概率预报首先应是“可靠的”，即能准确描述预报的不确定度，因为这是决策对错的基础。与此同时，也要追求高的“分辨率”(确定性的衡量)因为它会含有更多的信息，从而更有应用价值。根据用户对气象条件的依赖程度不一样，同一概率预报对不同的用户而言可能意味着截然不同的“确定预报”。譬如一个小概率预报对高风险用户而言，它就表示“有”, 而对低风险用户就是“没有”。也就是说“确定预报”其实是用户的函数。具体而言, 就是要运用“花费/损失”比等经济价值的计算方法来应用概率信息来决策。正是由于用户可以根据自身对气象条件的依赖程度来选择“预报”使自身的气象决策最优化，概率预报比单一值预报更有价值并适用于更广大的用户群, 其价值对于高风险用户尤其明显。这儿也进一步看到了我们在本文的姐妹篇^[1]中强调的，就是集合预报的主要任务是定量描述预报的不确定性以给出可靠的概率密度函数(分布)而不是提供一个更好的单一值确定预报。譬如, 由于集合平均预报(从统计意义上来说它比较准确)的光滑作用, 反而使它对较高风险的用户有害而无利。

文章进一步指出要提高气象预报的经济效益, 建立各行各业的行业气象决策模式是关键。气象工作者应该花大力气同用户建立关系, 了解他们的需要, 同他们合作以帮助他们建立合理的行业气象决策模式.同时对于低风险用户和广大普通民众而言, 也应发展一套合适的表达方式(如语言、图表、文字、颜色等)来清楚地传达预报的不确定性，这也是今后有待于调查研究和发展的重要课题。总之，由单一值预报向多值的概率预报转变不但是气象科学本身的要求而且是提高气象预报经济价值的需要，并有许多事需要跟上，特别是同用户的关系。现在是该理性地思考和设计未来天气、气候和水文等预报及服务体系的时候了^[28]。气象部门应该率先向公众和用户发布有关预报不确定性的信息，使他们有机会逐步熟悉和习惯预报的不确定性并最终在他们的决策过程中应用这些不确定性的信息。我们将在另文^[29]讨论具体的步骤和措施如何来实现这一宏伟的目标。