2. 中国气象局武汉暴雨研究所,武汉 430074;
3. 湖北省人工影响天气办公室,武汉 430074
2. Wuhan Heavy Rain Institute, CMA, Wuahn 430074;
3. Hubei Province Weather Modification Office, Wuhan 430074
20世纪90年代以来,气候变暖和极端天气事件格外引人关注[1-2]。极端天气事件是小概率事件,但是其影响制约着社会和经济的发展,甚至直接威胁到人类赖以生存的生态环境。研究结果表明我国近50年来,最高温度略有升高,最低温度则显著升高,日较差显著变小[3]。任福民等[4]、严中伟等[5]研究发现,在最近40~50年中,极端最低温度和平均最低温度趋于增高,我国北方极端最低气温普遍上升了5~10 ℃,同时冬季寒潮频率趋于降低、强度减弱,低温日数趋于减少。许多研究表明[6-8, 26],不同区域农业气象灾害对当地气候变化有着明显的响应。以上科研工作揭示了极端天气事件的某些变化规律,但是仍有一些科学问题值得更深入研究。比如区域气候变暖和极端天气事件的变化会有因果关系吗?也有研究认为极端天气事件的发生是气候变暖造成的[9, 27],那么怎样检测它们之间的这种因果关系等问题,都需要进一步的研究来加以探讨。
在气候诊断和预测的研究中,最常用的方法是计算两个变量的相关系数,当其达到一定显著性水平时就认为两个变量有某种因果关系或物理联系[10]。这种方法隐含着一种伪相关性,数据序列的自相关会影响不同变量间的互相关[11]。因此当考察序列间的联系时,应同时考察序列的自身变化和他因变化。那么怎样才能有效寻找不同变量间的因果关系或物理联系呢?目前气象学上关于气候变化的检测和归因技术主要包括多元回归分析和贝叶斯推断两大类,但是这些技术和方法在考察变量间的关系时,均没有同时考虑其自身的变化。
格兰杰因果性检验法[12-13]既考察变量间的相互关系又考虑其自身变化,可以有效避免虚假回归(伪相关)现象。格兰杰检验的基本着眼点是两个变量X与Y,即使它们高度相关,也不能说明X与Y之间一定存在因果关系,也可能存在其他因素,使X与Y之间显示出协同变化趋势,因此须对两个变量进行因果关系检验。该方法最早由Clive W. J. Granger于1969年提出,因其在经济学界的重要影响获得2003年度诺贝尔经济学奖。但是迄今,该方法很少在经济学领域之外得到应用。
本文将在简要介绍格兰杰因果性检验方法的基础上,将其应用于气候变量的实例分析和检验,以探讨武汉市气候变暖与极端天气事件之间的可能联系。
1 资料与方法 1.1 资料本文使用武汉气象站(站号:57494)1951—2007年逐日气温、降水、雷电、相对湿度、降雪、风和能见度等观测资料,按照相关气象标准,统计出武汉市1951—2007年年平均气温、平均最高气温、平均最低气温以及暴雨、雷暴、高温、闷热、降雪、低温、大风及雾等8类天气事件的日数。
测站变迁情况:1951年位于汉口王家墩机场(30°35′N、114°17′E),1952—1959年位于汉口赵家条231号(30°38′N、114°17′E),1960—2008年迁至汉口东西湖吴家山(30°37′N、114°08′E);迁站前后没有检测到气温突变。
1.2 方法 1.2.1 格兰杰因果性检验法的基本原理从统计学的角度,因果关系可以通过概率或者分布函数来表示。即在事件发生的所有其他情况固定不变的条件下,如果一个事件X的发生与否对于另一个事件Y发生的概率有影响,并且这两个事件在时间上存在先后顺序(X前Y后),那么就可以说X是Y的原因。
要确定严格的因果关系,必须考虑到完整的信息集。也就是说,要得出“X是Y的原因”这样的结论,必须全面考虑所有的事件。格兰杰提出因果关系的定义建立在完整信息集以及发生时间先后顺序基础上,它首先考察Y的当前值在多大程度上能被它的滞后值所解释,然后考察加上X后能否增进这种解释。如果能,则认为X能够导致Y,反之亦然。
令Ωn是到n时刻为止的所有信息,Xn为到n时刻为止所有的Xt(t=1,…,n),Yn+1为第n+1时刻的取值,Ωn-Xn为除X之外的所有信息。则如果:
| $ F({Y_{n + 1}}|{\mathit{\Omega} _n}) \ne F[{Y_{n + 1}}|({\mathit{\Omega} _n}-{X_n})] $ | (1) |
即可以认为变量X对变量Y有因果性,其中F为条件分布函数。由于无法得到所有信息Ωn,于是找一个可获取的信息集J来替代Ω:
| $ F({Y_{n + 1}}|{J_n}) \ne F[{Y_{n + 1}}|({J_n}-{X_n})] $ | (2) |
其次,在实际操作中检验变量的分布函数是否相等是非常困难的,更简便的方法是按照公式(3) 从数学期望值的角度来处理。如果
| $ E({Y_{n + 1}}|{J_n}) \ne E[{Y_{n + 1}}|({J_n}-{X_n})] $ | (3) |
就认为X含有对Y的预测信息。称满足式(3) 的为均值因果性,而满足式(2) 的为全面因果性。后来的发展逐渐过渡到从预测精度的角度来检验,即通过验证X的出现是否能减小对Yn+1的预测误差(σ)的方差,即:
| $ {\sigma ^2}({Y_{n + 1}}|{J_n}) < {\sigma ^2}[{Y_{n + 1}}|({J_n}-{X_n})] $ | (4) |
统计上通常用残差平方和来表示预测误差。在信息集J中,可建立X和Y的回归方程
| $ {Y_t} = \sum\limits_{i = 1}^k {{\alpha _i}{Y_{t - i}}} + \sum\limits_{i = 1}^k {{\beta _i}{X_{t - i}} + {e_t}} $ | (5) |
式中k为最大滞后阶数,et为误差项,αi,βi为Y和X的回归系数。
原假设为X不构成对Y的因果性,即:
| $ {H_0}:{\rm{ }}{\beta _1} = {\beta _2} =, \ldots, = {\beta _k} = 0 $ |
则在原假设成立的情况下有
| $ F = \frac{{(SS{E_r} - SS{E_m})/k}}{{SS{E_m}/\left( {N - 2k} \right)}} \propto F\left( {k, N - 2k} \right) $ | (6) |
式中SSEr为不考虑X情况下Y自身建回归时的残差平方和,SSEm为考虑X情况下同时建Y自回归的残差平方和。N为样本容量,k为最大滞后阶数。
| $ {\rm{若}}\;\;\;\;\;F \ge {F_\alpha } $ |
则否定原假设,即认为X能导致Y,表示为X→Y,X是Y的原因,式中Fα为显著性水平取α的F值。更详细的关于格兰杰因果性检验原理的论述见参考文献[12-14]。
1.2.2 序列的平稳性进行检验方法之一:ADF单位根检验格兰杰因果性检验要求所用的时间序列是平稳的,对于非平稳的时间序列,其均值、标准差或自相关函数等特征量都会随时间而变化,公式(6) 中统计量的渐进分布将不再是F分布,因而有可能出现虚假的因果关系。因此,进行格兰杰因果检验前应先对序列的平稳性进行检验。如果变量是平稳的,则可以进行因果性检验;如果变量是非平稳的,则需要对变量进行差分或取对数处理,直到变量变成平稳序列为止[13]。
ADF单位根检验(Augmented Dickey Fuller Test)是目前最有效的序列稳定性检验工具,它通过对原序列进行若干次差分变换得到平稳的序列,这种变换被证明不会改变原变量之间的因果关系[13]。ADF检验的基本原理[15]是根据t统计值判断,如果在序列无差分情况下的t统计值小于一定信度下的ADF临界值,则序列无单位根,认为原序列本身就是稳定的I(0) 序列;如果序列差分一次后成为平稳序列,则该序列是含有一个单位根的不稳定的I(1) 序列,如果序列第二次差分后成为平稳序列,则该序列是含有两个单位根的不稳定的I(2) 序列。
本文中ADF单位根检验通过Eview5.0商业软件(http://www.eviews.com/register)完成,检验时先设定一个显著性水平值(本文设为0.01),当ADF检验值小于0.01显著性水平值的ADF值时,认为被检验的序列为平稳序列。
1.2.3 极端天气事件的统计标准关于极端天气事件,参考中国气象局的标准[16]并结合武汉实际,作如下定义(表 1):
|
|
表 1 极端天气事件界定标准 Table 1 Determinant standards of extreme weather events |
从图 1给出的武汉市1951年以来的气温变化序列中可以很清楚地看到,近50多年来武汉市年平均气温、年平均最高气温和年平均最低气温均有升高的趋势,但升温的非对称变化很明显,年平均最低气温的增温幅度(0.45℃/10a)明显高于年平均最高气温的增幅(0.19℃/10a),表明武汉地区气候增暖主要是由于夜间温度的增加造成的,这与前人的相关研究结论一致[17-20]。
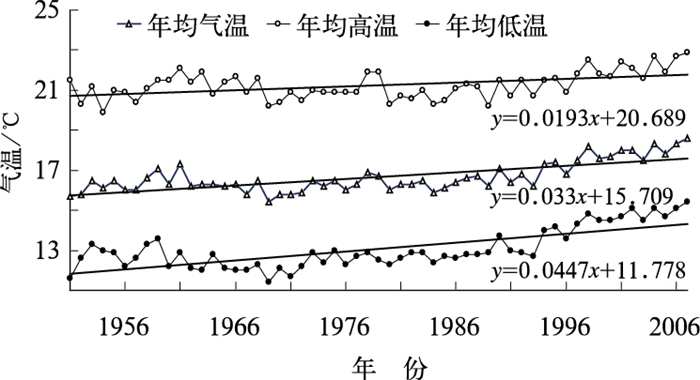
|
图 1 近57年来武汉市气温变化趋势 Fig. 1 The interannual change trends of the annual mean, and annual mean highest and lowest temperatures at Wuhan Station from 1951 to 2007 |
图 2给出的武汉市主要极端天气事件出现频率的变化表明,近57年来武汉地区高温和闷热天气事件有增多的趋势,其中闷热天气事件的增加趋势尤为明显,年平均增加量达到0.28 d。与之相反的是,雷暴、降雪、低温、大风、雾日均存在不同程度的下降趋势,下降幅度较明显的分别是雷暴、雾和低温事件,平均每年减少0.30 d、0.40 d和0.21 d。其次是大风和降雪事件,平均每年减少0.18 d和0.15 d。暴雨事件波动幅度很小。
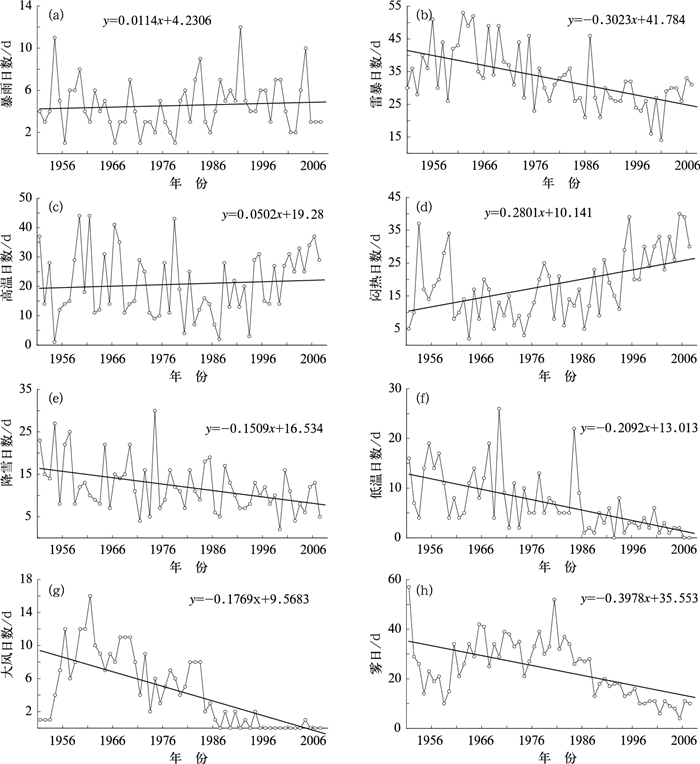
|
图 2 武汉8个极端天气事件逐年日数序列变化趋势(单位:d) (a)暴雨,(b)雷暴,(c)高温,(d)闷热,(e)降雪,(f)低温,(g)大风,(h)雾 Fig. 2 The interannual change trends for the annual day numbers in one year of 8 kinds of extreme-weather events at Wuhan during 1951 to 2007 (unit: d) (a) heavy rain, (b) thunderstorm, (c) high temperature, (d) mugginess, (e) snowfall, (f) low temperature, (g) strong wind, and (h) fog |
计算表明,武汉年平均气温与当年绝大部分极端天气事件的出现频率之间具有高相关性(表 2中滞后期为0年的行)。其中与高温、闷热天气日数的正相关系数,以及与雷暴、降雪、低温、大风和雾日的负相关系数均超过0.01的信度标准。由于年平均气温的变化在一定程度上是较平稳的,在滞后期分别取1、2年(即极端天气事件落后年平均气温1年、2年)时,这种高相关程度略有降低;而在滞后期分别取-2、-1年(即年平均气温分别落后极端天气事件2年、1年)时,这种高相关程度大多略有降低,少数极端天气如雷暴、大风与平均气温相关程度略有增大。尽管相关程度有所变化,但总体上看相关关系依然显著。表现在其与闷热天气日数的正相关系数,以及与雷暴、低温、大风和雾日数的负相关系数仍然保持在较高的水平,超过了0.01的信度标准。
|
|
表 2 武汉市年平均气温与极端天气事件相关系数(滞后期取-2,-1,0,1,2年) Table 2 The relationship between the annual mean temperature and extreme weather events at Wuhan(the lag period is -2, -1, 0, 1, 2 years) |
此外还发现,在某些极端天气事件之间也有很高的相关系数(表 3),如雷暴日数与低温、大风等事件之间的负相关,高温与闷热天气事件之间的正相关,闷热日数与低温、大风、雾之间的负相关,降雪与低温事件之间的正相关,低温与大风、雾之间的正相关,以及大风事件与雾日之间的正相关,其相关系数也超过0.01的信度标准。有些相关没有物理意义,但可能有统计意义,如雷暴日数(多出现在夏半年)与低温日数(多出现于冬季)、大雾日数(多出现于冬半年)。暴雨事件则与任何其他极端天气事件均无明显相关性。
|
|
表 3 武汉市各种极端天气事件之间的相关系数 Table 3 The correlation coefficient among various extreme weather events at Wuhan |
关于武汉及华中地区未来气候仍将继续变暖的趋势已经得到诸多研究的认同[19-20],如果能够确定年平均气温与某些极端天气事件之间存在因果关系,则可以据此来预测武汉未来极端天气事件的变化趋势,这将具有非常重要的价值。由于可能出现伪相关现象,仅从相关系数上无法确定它们之间是否存在可信的因果关系,以下将应用格兰杰因果性检验方法来对它们之间的关系进行归因分析和检验。
2.3 武汉市平均气温与极端天气事件的格兰杰因果性检验结果首先对上述各序列进行ADF检验,结果(表 4) 表明,原序列中除低温事件本身即为平稳序列外,其他变量通过一次差分变换后均可转为平稳序列。
|
|
表 4 ADF单位根变换结果(取信度标准为0.01) Table 4 Results of ADF unit root transform(confidence degree exceeds 0.01 standard value) |
对于经过ADF检验后得到的平稳序列,就可以进行格兰杰因果性检验。本文在应用Eview5.0软件进行格兰杰因果检验时,设定0.01的临界置信概率,即当检验的信度小于0.01时,接受原假设。由于格兰杰因果性检验对变量的滞后有很强的敏感性,目前对于滞后期的具体选择在学术界还存在争议,多数观点认为最好使用几个滞后期[21]。在本文中,将滞后期选为1~3年。此外,由于格兰杰因果检验软件目前只能给出变量之间是否存在因果关系,而不能确定这种因果关系的正负。
表 5给出的是格兰杰因果检验得到的具有因果关系的变量列表。可见:(1) 年平均气温的升高是次年闷热天气事件增多的原因之一,也可能是导致次年降雪事件减少的重要因素;(2) 大风和低温事件的变化可能是导致次年平均气温发生变化的主要原因。
|
|
表 5 格兰杰因果性检验结果 Table 5 The results of Granger causality detection |
由于格兰杰检验目前只能给出变量之间是否存在因果关系,还不能给出所得因果关系的方向性,因此还需结合前文中计算的相关性符号来加以理解。从物理机制分析来看,有研究指出[22-25],全球变暖不仅使地面和低层空气明显变暖,相应的高温热浪还会使地表蒸发加剧,引发干旱事件频次增加、范围增大,同时大气保持水分的能力增强,这意味着大气水分可能增长。气候增暖之后,气候系统中水循环过程加剧,降水率增强,引起大气潜热释放增加,水分和能量循环的改变,是强对流天气、极端天气事件产生变化的重要因素。我们分析了武汉市年降水日数和年大雨以上日数的变化,发现57年来武汉市年雨日也在显著减少,气候倾向率为-6.2 d/10a,这种变化跟雷暴日数减少是一致的;而大雨日数却有小幅上升,增幅为0.4 d/10a,表明强降水有增多的趋势。另外,分析还得出年平均雨强(年降水总量/年雨日)57年来正在以0.5 mm/10a增幅变化。综上分析,57年来武汉市降水有增强的变化特点。因此,对以上因果关系的物理解释是很明了的,气候变化本身具有很强的持续性[11],前文分析已经表明,武汉气候变暖主要表现为最低气温的增加,这种结果必然会导致冬季低温降雪事件的减少和夏季闷热事件的增多。另一方面,武汉低温和大风事件一般是伴随寒潮天气过程而发生的,冷空气活动越少,强度越弱,区域陆地表层能量储备越多,进而经长波辐射给大气吸收的能量越多,气温就会越高。
我们注意到,通过格兰杰因果性检验得到的这些因果关系与前文计算的相关性有很大的不同,某些事件之间具有高相关性,如表 2中的年平均气温与高温、雷暴、低温、大风和雾日的同期及滞期为-2、-1、0、1、2年时其相关系数均超过0.01的信度标准。但是格兰杰因果检验结果发现它们之间并无明显的因果关系,并且,从物理机制上也很难找到这些高相关特性的合理解释。因此我们认为它们之间的这种高相关性极有可能只是一种伪相关现象或者仅是一种统计学上的高相关现象。
3 小结与讨论(1) 近57年来武汉市年平均最低气温增幅为0.45 ℃/10a,明显高于年平均最高气温0.19 ℃/10a的增幅,可见气候变暖主要是由夜间气温升高所致;高温和闷热天气事件为增多趋势,其中闷热天气事件最明显,达到2.8 d/10a,而年雷暴、降雪、低温、大风、雾日则均为下降趋势,雷暴、雾和低温事件降幅明显,每10年减少3.0 d、4.0 d和2.1 d。大风和降雪事件,每10年减少1.8 d和1.5 d。暴雨事件波动幅度很小。
(2) 相关分析表明,年平均气温与当年及滞后-2、-1、0、1、2年的极端天气事件具有高相关性;格兰杰因果性检验结果表明,年平均气温的升高可能是影响次年闷热天气事件增多的因素,并会导致次年降雪事件减少;而大风和低温事件的变化可能是导致次年平均气温发生变化的主要原因。这与简单相关结果有很大的不同,如年平均气温与高温、雷暴、低温、大风和雾日等相关极显著,但格兰杰因果检验发现它们并无明显因果关系,极可能是伪相关。
需要说明的是,实际上无法得到所有信息集,因而经过格兰杰因果性检验得到的因果关系也可能是不完备的,可能会遗漏重要的因子。所以,经过格兰杰因果性检验得到的也可能只是统计上的必要条件,不是充分条件,但检验结果仍能使应用者增强因果性的信心。
格兰杰因果性检验作为气候变化检测与归因的一种新方法,无疑将是天气预报和气候分析中初选有物理意义的因子的一种有效手段。
王维国, 王秀荣, 2008. 2007年城市极端天气事件及其危害分析[J]. 气象, 34(4): 16-21. DOI:10.7519/j.issn.1000-0526.2008.04.002 |
杨馥祯, 吴胜安, 2007. 近39年海南岛极端天气事件频率变化[J]. 气象, 33(3): 107-112. DOI:10.7519/j.issn.1000-0526.2007.03.016 |
翟盘茂, 任福民, 1997. 中国近四十年最高最低温度变化[J]. 气象学报, 55(4): 418-529. DOI:10.11676/qxxb1997.042 |
任福民, 翟盘茂, 1998. 1951—1990年中国极端气温变化分析[J]. 大气科学, 22(2): 217-227. |
严中伟, 杨赤, 2000. 近几十年中国极端气候变化格局[J]. 气候与环境研究, 5(3): 267-272. |
冯明, 刘可群, 2007. 湖北省气候变化与主要农业气象灾害的响应[J]. 中国农业科学, 40(8): 1646-1653. |
刘可群, 陈正洪, 张礼平, 等, 2007. 湖北省近45年降水气候变化及其对旱涝的影响[J]. 气象, 33(11): 58-64. DOI:10.7519/j.issn.1000-0526.2007.11.009 |
王希娟, 唐红玉, 2006. 青海春季降水的气候变化特征及其对春旱的影响[J]. 气象, 32(5): 41-45. DOI:10.7519/j.issn.1000-0526.2006.05.007 |
周秀杰, 张桂华, 郑红, 等, 2004. 黑龙江省气候变暖对极端天气气候事件的影响[J]. 气象, 30(11): 47-50. DOI:10.3969/j.issn.1000-0526.2004.11.011 |
黄嘉佑, 1990. 气象统计分析与预报方法[M]. 北京: 气象出版社.
|
曹鸿兴, 1993. 大气运动的自忆性方程[J]. 中国科学:B辑, 23(1): 104-112. |
Granger C W, 1969. Investigating causal relations by econometric models and cross-spectral methods[J]. Econometrica, 37(3): 27-39. |
Granger C W, 1986. Developments in the study of cointegrated economic variables[J]. Oxford Bull Economics and Statistics, 48(3): 213-228. |
曹永福, 2005. 格兰杰因果性检验评述[J]. 世界经济统计研究, (52): 16-21. |
陈昭, 2008. 时序非平稳性ADF检验法的理论与应用[J]. 广州大学学报(自然科学版), 7(5): 5-10. |
中国气象局, 1990. 重要天气预报质量评分办法[M]. 北京: 气象出版社, 15-57.
|
陈正洪, 1998. 湖北省60年代以来平均气温变化趋势初探[J]. 长江流域资源与环境, 7(4): 341-346. |
唐红玉, 翟盘茂, 王振宇, 等, 2005. 1951-2002年中国平均最高、最低气温及日较差变化[J]. 气候与环境研究, 10(4): 728-735. |
黄嘉佑, 胡永云, 2006. 中国冬季气温变化的趋向性研究[J]. 气象学报, 64(5): 614-621. DOI:10.11676/qxxb2006.060 |
史瑞琴, 陈正洪, 陈波, 2008. 华中地区2030年前气温和降水量变化预估计[J]. 气候变化研究进展, 4(3): 173-176. |
易会文, 2006. 格兰杰因果检验用法探讨[J]. 中南财经政法大学研究生学报, (5): 77-79. |
Trenberth K E, 1998. Atmospheric moisture residence times and cycling:Implications for rainfall rateswith climate change[J]. ClimChange, 39: 667-694. |
Qian W, Fu J, Yan Z, 2007. Decrease of light rain events in summer associated with a warming environment in China during 1961-2005[J]. Geophys Res Lett, 34: L11705. DOI:10.1029/2007GL029631 |
Tu K, Yan Z, Dong W, 2010. Climatic jumps in precipitation and extremes in drying North China during 1954-2006[J]. Journal of Meteorological Society of Japan, 88(1): 29-42. DOI:10.2151/jmsj.2010:103 |
GoswamiB N, Venugopal V, Sengupta M S D, et al, 2006. Increasing trend of extreme rain events over India in a warming environment[J]. Science, 314: 1442-1445. DOI:10.1126/science.1132027 |
高霞, 王宏, 于成文, 等, 2009. 近45年来河北省极端降水事件的变化研究[J]. 气象, 35(7): 10-15. DOI:10.7519/j.issn.1000-0526.2009.07.002 |
张天宇, 程炳岩, 刘晓冉, 等, 2008. 重庆极端高温的变化特征及其对区域性增暖的响应[J]. 气象, 34(2): 69-76. DOI:10.7519/j.issn.1000-0526.2008.02.010 |
罗伯良, 张超, 林浩, 2008. 近40年湖南省极端强降水气候变化趋势与突变特征[J]. 气象, 34(1): 80-85. DOI:10.7519/j.issn.1000-0526.2008.01.012 |
 2010, Vol. 36
2010, Vol. 36 
 "(闻雷)记录
"(闻雷)记录