2. 江苏省气象台,南京 210008;
3. 南京信息工程大学大气科学学院,南京 210044
2. Jiangsu Meteorological Observatory, Nanjing 210008;
3. College of Atmospheric Sciences, Nanjing University of Information Science and Technology, Nanjing 210044
心脑血管疾病是心血管和脑血管疾病的统称,是威胁人类健康造成死亡的主要疾病,其发病率和死亡率占各种疾病的首位。据统计[1],世界上有1/3的人患有心脑血管疾病,每年有1500万人被心脑血管疾病夺去生命,占总死亡人数的3/5以上。我国每年因心脑血管疾病造成死亡的人数约260万[2]。国内外诸多研究表明[3-6],气象条件是心脑血管疾病发病和死亡的诱因之一。
医疗气象预报是根据天气、气候或气象因子与某些疾病的关系,运用医疗气象的研究方法和天气预报的手段,预报未来特定的气象条件对此类疾病发生、加重或缓冲可能产生的影响[7]。近年来,由于人们生活水平不断提高,关于医疗气象预报的研究也得到更多的关注和重视[8-10]。目前,国内的心脑血管疾病的预报研究采用逐步回归法[11-12]、自动交互检测方法(AID)[13]等,主要是将气象因子和发病或就诊人数确立统计关系来建立预测模型。武汉市[14]分四季建立了心脑血管疾病日发病率的气象预报模型,并结合天气过程演变开发了医疗气象预报系统,对公众发布疾病等级预报。
然而必须明确的是,气象条件仅是诱发心脑血管疾病的环境因素之一,其他原因对其发病的影响往往蕴含在发病率的周期变化和趋势变化中[15],尤其是某医院的就诊人数和临床发病人数有着明显的区别,还受到节假日、专家门诊日等社会或经济因素的制约。因此,有必要考虑这些因子的综合影响,设计比单纯考虑气象因子更精确的预测模型。本文引入计量经济学中的虚拟变量来刻画非气象因子对心脑血管疾病的影响,然后通过逐步回归方法筛选出对心脑血管疾病有显著贡献的气象和非气象因子,最后用支持向量机方法构建南京市心脑血管疾病的预测模型,并进行预报试验。
1 资料与方法 1.1 资料本文采用的医疗数据是南京某医院2003年1月至2008年7月心血管和脑血管的逐日就诊人数资料,各2038例。该医院为三级甲等综合性医院,其中心血管病为其重点特色专科,在地域和人员上具有一定的代表性。同期气象资料来自南京国家气候基准站,包括气温、气压、相对湿度、风速、露点、降水等共23个气象要素。
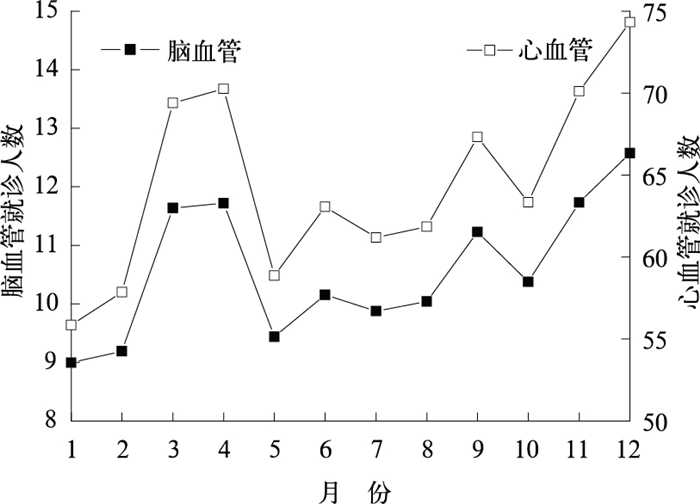
用2003—2007年的逐日资料统计了心血管和脑血管疾病的月平均及周平均就诊人数。从图 1和图 2可以看出,心血管和脑血管就诊人数的月、周分布基本一致,但心血管的就诊人数明显多于脑血管,这可能是由于该医院心血管为特色专科的缘故。
|
图 1 2003—2007年南京市心、脑血管疾病各月平均就诊人数 Fig. 1 Average cardiovascular (hollow square) and cerebrovascular (solid square) disease numbers of each month from 2003 to 2007 in Nanjing |
|
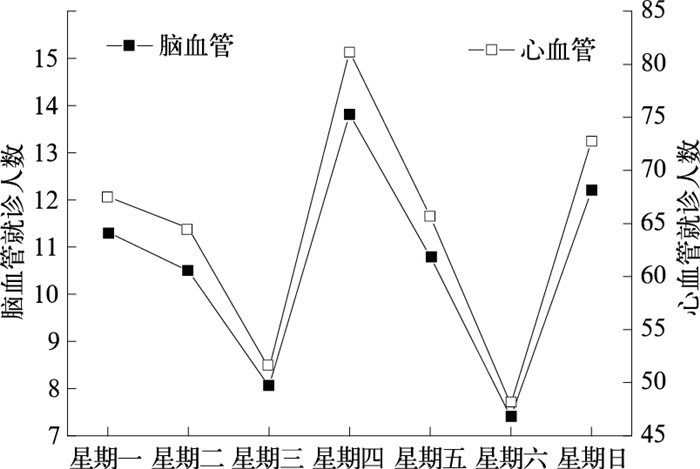
图 2 2003—2007年南京市心、脑血管疾病一周每日平均就诊人数 Fig. 2 Average cardiovascular (hollow square) and cerebrovascular (solid square) disease numbers in Nanjing in a week from 2003 to 2007 |
一年中,12月份的就诊人数最多,心血管平均有74人,脑血管平均有13人,其次是3月和4月。这和武汉市[16]、银川地区[11]、湖州市[13]冬春季发病高于夏秋季的结论基本一致。冬季和春季温度较低,强冷空气易引起气温骤降,气压升高,湿度降低,研究表明[17-19],这些气象要素的变化都是促使心脑血管发病的有利条件。另外发现,国家法定节假日(春节、五一和十一)所在月份均为全年的就诊低谷,这主要是由于节假日期间专家坐诊时间的缩减。
南京市心脑血管疾病一周平均就诊人数分布如图 2所示,周三和周六为就诊的低谷(这与该医院门诊制度有关),紧接着周四、周日迎来就诊的高峰,其中周四就诊人数最多,脑血管平均达14人,心血管平均为81人。以上统计结果表明,南京市心脑血管疾病的逐日就诊人数存在明显的月变化和周变化,而造成这种变化的原因是多重的,气象因素仅仅是诱发心脑血管疾病的环境因素之一。
1.2 SVM回归方法在信息量较大,而预报对象和预报因子的关系又不甚清楚的情况下,智能机器学习方法是解决这类问题的较好手段[20]。本文采用的支持向量机(SVM)方法是一种新的处理非线性分类和回归的有效方法,它以统计学理论为基础,对小样本条件下的非线性映射具有优势[21],近年来在气候预测领域得到较好的应用[22-29]。
SVM回归方法的基本思想是基于Mercer核展开定理,通过非线性映射φ,把样本空间映射到一个高维乃至于无穷维的特征空间(Hilbert)空间,在特征空间中引入ε——不敏感误差函数,定义最优线性回归超平面,把寻找最优线性回归超平面的算法归结为求解一个凸约束条件下的一个凸规划问题,简单地说就是升维和线性化。SVM回归方法的最终决策函数只由少数的支持向量所确定,其余样本对最优超平面没有贡献,模型的复杂程度仅取决于支持向量的数目和核函数的计算。其基本原理和方法参见文献[21-22]。
本文采用中国气象局培训中心开发的CMSVM软件平台建立模型,它对数据的文件格式有一定要求。首先要对各个因子进行归一化处理,这有利于避免各个因子间的量级差异,使每一个因子的数据落入区间[0, 1],归一化方式为:(x-xmin)/(xmax-xmin)。
由于构造支持向量机的基础是Mercer定理,作为建立支持向量机的核函数必须以满足Mercer定理的条件为前提,因此本文我们选择径向基函数(满足Mercer定理条件)作为核函数建立SVM回归模型。径向基函数形为:K(x, xi)=exp(-r‖x-xi‖2),其中xi为作为支持向量的样本因子向量;x为待预报因子向量;r为核参数。
2 预报因子的筛选虽然上述SVM方法对预报因子的个数没有明显的限制,但所选的预报因子应尽量包含对预报对象有明确意义的信息,从而使预报更加准确。逐步回归方法是医疗气象研究中常用的方法之一,它可以选出对预报量有显著贡献的因子,本文用它来对心脑血管疾病可能有影响的气象因子和非气象因子进行筛选,得出最后用于SVM回归建模的解释变量。
2.1 气象因子的筛选用逐步回归法分别筛选对心血管和脑血管疾病影响较为显著的气象因子,样本的建立采用经典的统计方法,即用上一天的气象因子对应当天的就诊人数,最后得到方程如下:
| $ \begin{array}{l} {Y_{脑血管}} = 9.5858 + 0.19226{T_{{\rm{ave}}}} - \\ 0.22698{E_{{\rm{max}}}} + 0.025874R{H_{{\rm{ave}}}} \end{array} $ | (1) |
复相关系数:R=0.104, F=7.0918 > F0.05
| $ \begin{array}{l} {Y_{心血管}} = 58.976 + 0.96756{T_{{\rm{ave}}}} - \\ 1.127{E_{{\rm{max}}}} + 0.13341R{H_{{\rm{ave}}}} \end{array} $ | (2) |
复相关系数:R=0.100, F=6.6254 > F0.05
其中,Tave为日平均气温(℃),Emax为日最高水汽压(hPa), RHave为日平均相对湿度(%)。可见,心血管和脑血管疾病均选出日平均气温、日最高水汽压和日平均相对湿度为显著气象因子,且方程的显著性较好,但方程对因变量Y的解释能力不高。
2.2 非气象因子的构建与筛选考虑到气象因子仅仅是心脑血管疾病就诊人数的关联因素之一,所以有必要引进对就诊人数影响较大的非气象因子。注意到通常特定的时间段里心脑血管疾病的就诊人数存在有规律的变化,比如节假日就诊人数少、由于医院的作息制度导致一周内就诊人数有多有少等。本文采用计量经济学中的虚拟变量来刻画这些因素的影响,每个虚拟变量只能取值1或0。结合医院就诊人数的时间分布特征,构造如下20个虚拟变量:
节假日虚拟变量1个(Jt)。Jt代表元旦、五一国际劳动节、十一国庆节、春节。其中前三个节日的时间相对固定,而春节根据阴历有所变动,在这些节日期间Jt取1,其他时间取0。一般而言,节假日期间专家坐诊的时间缩减,就诊人数也会相应减少。
星期虚拟变量7个(Wit),代表由于医院制度和患者作息时间而引起的一周就诊人数变化。i=1, 2, …, 7,分别代表周一、周二、…、周日,如果第t天为周二(i=2),则W2t=1,其他Wit(i≠2) 取0,以此类推。
月份虚拟变量12个(Mjt),代表由于经济、社会等非气象因素引起的不同月份的就诊人数变化。j=1, 2, …, 12,分别代表 1月、2月、…、12月,取值类似于星期虚拟变量。
虚拟变量是定性变量,在计量经济学中,当定性变量有m个类型时模型不能引入m个虚拟变量,否则它们之间会产生完全多重共线性[25]。而本文中由于要对其进行筛选,因此一开始可以把它们先全部放入模型中。
另外,考虑到心·脑血管疾病的发病和就诊具有某种惯性,即在某段时期内会集中出现或者集中不出现,为考察这种惯性(经济学中称之为自回归效应),故在模型中加入解释变量的滞后项Y(-1) 和Y(-7)。
用逐步回归方法筛选由20个虚拟变量和2个滞后项构成的非气象因子,由于二者的取值相对固定,样本的构建用当天的因子对应当天的就诊人数,最后得到有显著贡献的因子如下(回归方程ɑ=0.01):
脑血管(共7个):节假日虚拟变量Jt;周三、周四、周六、周日的星期虚拟变量W3t, W4t, W6t, W7t;滞后项Y(-1) 和Y(-7)。
心血管(共7个):节假日虚拟变量Jt;周二、周四、周日的星期虚拟变量W2t, W4t, W7t;10月的月份虚拟变量M10t;滞后项Y(-1) 和Y(-7)。
综上,用逐步回归方法对心血管和脑血管的影响因子进行筛选,均得到3个气象因子和7个非气象因子。下面我们将进行两次预报试验,一是仅用筛选的3个气象因子作为预报因子,二是用得到的共10个气象和非气象因子构成预报因子集,两者均以逐日的就诊人数作为预报对象,分别建立SVM回归预测模型。
3 建模及预报结果检验 3.1 SVM回归建模用2003年1月至2008年4月的样本资料(两组均为1940个)建立模型,分别按照75%(1455个)、20%(388个)和5%(97个)的比例构建训练集、实验集和检验集。用2008年5—7月的样本资料(两组均为91个)构建预报集,即用最优回归模型对2008年5—7月的心、脑血管疾病的逐日就诊人数进行预报。
3.2 预报分级为方便预报检验,我们统计出2003—2007年心、脑血管疾病的平均就诊人数,以平均值的±20%定为中等,然后依次递增或递减40%,将就诊人数预报划分为5个等级[9](如表 1)。
|
|
表 1 就诊人数预报分级 Table 1 Forecast for grade classification of disease numbers |
用逐步逼近法最优化参数,经过反复训练,最终确定了南京市心、脑血管疾病预报模型的参数,其中c为惩罚系数、w为回归管道带宽、g为核参数,并通过CMSVM预报程序计算出最优模型对2008年5—7月逐日就诊人数的预报结果。
若仅用气象因子作为预报因子建立模型进行预报,则心、脑血管疾病就诊人数预报值与真实值的相关系数分别为0.029和0.038,均不能通过显著性检验;且预报值比较平稳,不能反映出随时间的起伏,心血管就诊人数集中在60~80人(3、4级),脑血管就诊人数集中在10~13人(3级)。这表明,仅用气象因子建立的疾病预测模型,不能取得较好的预报结果。
而用气象和非气象因子构成的预报因子集,通过SVM回归方法建立的心、脑血管疾病预测模型对2008年5—7月逐日就诊人数的预报结果显示(如表 2),预报值与真实值的相关系数分别为0.60和0.48,均通过了α=0.01的显著性检验。另外,按照就诊人数预报分级,心血管和脑血管的预报结果和真实值在同一个等级的准确率分别为48.35%和37.36%,在同一等级和差一等级的准确率分别为87.91%和84.62%,预报结果较为满意。
|
|
表 2 SVM最优模型参数及预报结果 Table 2 Parameters and forecast results of the best SVM models |
另外,从预报值和真实值的对比(图 3) 可以看出,预报值能较好地反映真实值的变化趋势,可见,引入虚拟变量刻画非气象因子有助于提高基于气象因子的心脑血管疾病预测模型。但模型同时也显示出对极值的预测水平较弱,这主要是由于影响心脑血管疾病的就诊人数的因素除本文重点考虑的气象和非气象因子外,尚有一些涉及病理学方面的难以量化的因素,比如工作压力、饮食习惯等,而这些因素恰恰是直接诱发心脑血管疾病的元凶。

|
图 3 SVM对心、脑血管疾病逐日就诊人数的预报结果对比 Fig. 3 Comparison between the cerebrovascular (a) and cardiovascular (b) disease numbers (dotted) everyday forecasted by SVM and the real disease numbers (solid) |
本文采用虚拟变量刻画非气象因子,通过逐步回归筛选气象和非气象因子,然后基于SVM法构建了南京市心脑血管疾病的预测模型,主要结论有:
(1) 引入虚拟变量刻画非气象因子有助于提高基于气象因子的心脑血管疾病预测模型。
(2) 对心脑血管疾病求诊人数影响显著的气象因子是日平均气温、日最高水汽压和日平均相对湿度。
(3) 将求诊人数分为5个等级,采用此分级预测方法,模型针对心脑血管疾病同一等级或差一等级的准确率较高,实际预测结果较好,证明该预测模型和方法具有实际业务应用价值。
路凤, 金银龙, 陈义斌, 2008. 气象因素与心脑血管疾病关系的研究进展[J]. 国外医学卫生学分册, 35(2): 83-87. |
刘方, 张金良, 陆晨, 2004. 我国气象因素与心脑血管疾病研究现状[J]. 气象科技, 32(6): 425-437. |
王宝金, 1992. 健康·环境·天气[M]. 北京: 气象出版社, 94-98.
|
Pan W H, Li L, Tsai M J, 1995. Temperature extremes and mortality from coronary heart disease and cerebral infarction in elderly Chinese[J]. Lancet, 345(8946): 353-355. DOI:10.1016/S0140-6736(95)90341-0 |
张书余, 王宝鉴, 谢静芳, 等, 2010. 吉林省心脑血管疾病与气象条件关系分析和预报研究[J]. 气象, 36(9): 106-110. DOI:10.7519/j.issn.1000-0526.2010.09.017 |
刘利群, 潘小川, 郑亚安, 等, 2008. 气象因素与心脑血管疾病急诊人次的时间序列分析[J]. 环境与健康杂志, 25(7): 578-582. |
杨贤为, 1999. 医疗气象预报的进展[J]. 气象知识, (1): 8-9. |
张德山, 孙培源, 赵娜, 等, 2008. 北京市感染性腹泻疾病的医疗气象预报与应用研究[J]. 气象, 34(10): 90-95. DOI:10.7519/j.issn.1000-0526.2008.10.012 |
山义昌, 徐太安, 郑学山, 等, 2001. 潍坊市四类疾病与气象环境的关系[J]. 气象, 27(11): 52-54. DOI:10.3969/j.issn.1000-0526.2001.11.012 |
沈树勤, 严明良, 尹东屏, 等, 2003. 江苏环境气象指数开发技术初探[J]. 气象, 29(2): 17-20. DOI:10.7519/j.issn.1000-0526.2003.02.004 |
马玉霞, 郑有飞, 张成祥, 2003. 银川地区冠心病发病率预报模型[J]. 气象科技, 31(2): 94-96. |
卢爱梅, 徐红梅, 高瑾, 等, 1997. 齐齐哈尔市心、脑血管疾病发病与气象因素的关系及其预测预报研究[J]. 中国慢性病预防与控制, 5(2): 61-63. |
韩建康, 刘小琦, 顾志伟, 2008. 湖州市心脑血管疾病与气象因素的关系分析及预报研究[J]. 浙江预防医学, 20(12): 8-16. DOI:10.3969/j.issn.1007-0931.2008.12.004 |
陈正洪, 杨宏青, 张鸿雁, 等, 2001. 武汉市呼吸道和心脑血管疾病气象预报研究[J]. 湖北中医学院学报, 3(2): 15-17. |
杨贤为, 叶殿秀, 2003. 我国心脑血管病的医学气象研究[J]. 气象科技, 31(6): 376-380. |
陈正洪, 杨宏青, 曾红莉, 等, 2000. 武汉市呼吸道和心脑血管疾病的季月旬分布特征分析[J]. 数理医药学杂志, 13(5): 413-415. |
叶殿秀, 杨贤为, 吴桂贤, 2003. 京、沪两地脑卒中发病率及其预测模型[J]. 气象科技, 31(6): 381-384. |
刘世玲, 刘济跃, 李志莉, 等, 1999. 脑血管发病和气象条件的关系[J]. 临床神经病学杂志, 12(2): 76-78. |
邰庆国, 周彩桂, 周大魁, 等, 2001. 临沂市急性心肌梗塞与气象因素的关系[J]. 山东气象, (2): 27-28. |
冯汉中, 陈永义, 成永勤, 等, 2006. 双流机场低能见度天气预报方法研究[J]. 应用气象学报, 17(1): 94-99. DOI:10.11898/1001-7313.20060116 |
Vapnik V N. Statistical Learning Theory[M].John Wiley & Sons, Inc., New York, 1998.
|
陈永义, 俞小鼎, 高学浩, 等, 2004. 处理非线性分类和回归问题的一种新方法(Ⅰ)——支持向量机方法简介[J]. 应用气象学报, 15(3): 345-354. |
冯汉中, 陈永义, 2004. 处理非线性分类和回归问题的一种新方法(Ⅱ)——支持向量机方法在天气预报中的应用[J]. 应用气象学报, 15(3): 355-365. |
毛宇清, 王咏青, 王革丽, 2007. 支持向量机方法应用于理想时间序列的预测研究[J]. 气候与环境研究, 12(5): 676-682. |
冯汉中, 陈永义, 2005. 支持向量机回归方法在实时业务预报中的应用[J]. 气象, 30(1): 42-45. |
郭虎, 王建捷, 杨波, 等, 2008. 北京奥运演练精细化预报方法及其检验评估[J]. 气象, 34(6): 19-27. |
熊秋芬, 顾永刚, 王丽, 2007. 支持向量机分类方法在天空云量预报中的应用[J]. 气象, 33(5): 22-28. |
李智才, 马文瑞, 李素敏, 等, 2006. 支持向量机在短期气候预测中的应用[J]. 气象, 32(5): 58-62. |
常涛, 2006. 支持向量机在大气污染预报中应用研究[J]. 气象, 32(12): 63-67. |
张晓峒, 2001. 计量经济学基础[M]. 天津: 南开大学出版社.
|
 2010, Vol. 36
2010, Vol. 36 