2. 国家气象中心,北京 100081
2. National Meteorological Center, Beijing 100081
杜钧和陈静[1]不久前在《气象》杂志上就公众对气象预报的指责事例讨论了天气预报制作和服务方式应该改革的问题。指出预报的不确定性也应该作为预报的不可分割的一部分定量地告知用户和公众。概括地来说,天气预报如果只是单一值的决定论式预报,那么它是不完备的[2]。这种预报至少有以下四大“罪状”(当然,做决定论式预报的原意是良好的,并且在大多数情况下预报员自己并没有意识到这些不足,所以这儿并不是责怪,而是指出这些不足以便今后可以改进)——“不科学的、害人的、害己的、不诚实的”。由于大气系统的混沌性以及观测和模式的不确定性,预报不确定性是必然的[3-4]。所以决定论的单一值预报是“不科学的”也是不可能做到100%准确的。我们知道气象用户是多样性的,他们对气象的依赖程度各有不同。有些对气象条件很敏感,一旦受灾,经济损失巨大; 反之,有些对气象条件就不那么依赖。对于前一类用户,对某一严重气象事件事先哪怕有一丁点儿的预报信息,就会对他们的决策过程有很重要的帮助。所以,能够把预报的不确定性定量化并事先告知广大用户,那么不同的用户就能根据自身对气象条件的依赖程度来做出不同的最佳决策以达到最好的经济和社会效益。但单一值的预报往往对第一类的用户没有用处反有害处[5],所以是“害人的”。在现实世界里,大气的实况同单一值的预报总有这样那样的差异(注意,这里除了大气的可预报性限度外,还有一个如何正确检验预报的问题[1]),所以公众总认为我们的预报不准确并对预报失去信心。这样就会常常招致公众和用户对气象部门的指责。所以,这就是“害己的”一面。最后,当我们发布单一值的确定预报时,就暗示着我们对这一预报有100%的把握。显然,它是有点自欺欺人、是“不诚实的”。关于更多预报不确定性问题的讨论,读者可以进一步阅读文献[2]。文献[2]的中文版出版工作也正在进行中,它的介绍和讨论可参考文献[6]。
所以,天气预报从单一值的决定论向多值的概率论转变不但符合气象科学的实际,也是更好地服务社会之必需。当然这种转变不是轻而易举的,因为人们已经习惯了这种决定论的思维方式。本文就有关这种转变所面临的一些普遍困惑谈一些想法,希望它对这一变革能起积极的推动作用。因为集合预报是促成这种转变的核心技术,所以本文首先讨论如下几个问题:为什么要做集合预报?集合预报的根本目的是什么?人们常常对集合预报有哪些误解?集合预报对整个数值预报体系将带来什么样的变革?以及预报员的新使命是什么?
1 为什么要做集合预报科学的最终目的是预测未来。一个预报系统大致有四个基本环节组成:资料收集(观测)、观测资料被处理和加工为适用于数值模式的初值(资料同化)、预报模式从初值推测未来的状态(模式积分)、以及预报信息被应用到实际问题中(预报信息的处理和交流、用户的理解和决策)。在上面的任何一个环节中,都不可避免地会产生一些不确定性。譬如,观测过程中存在仪器误差和人为误差,资料同化中不符合实际的数学假定,模式物理过程仅仅是实际大气系统的一个近似而已,模式格点的不连续性和截断误差等,不同预报员和用户或同一预报员和用户在不同的条件下(经验、知识、时间、地点、心情和事态等)可能对同一模式结果或预报存在不同理解和决策等等。很多以上这类误差在现实中往往是不可避免的,甚至是不可知的。
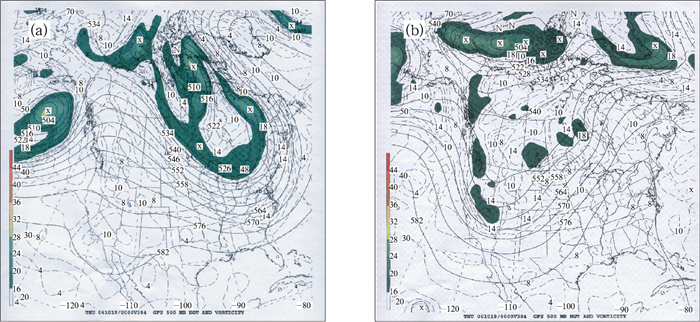
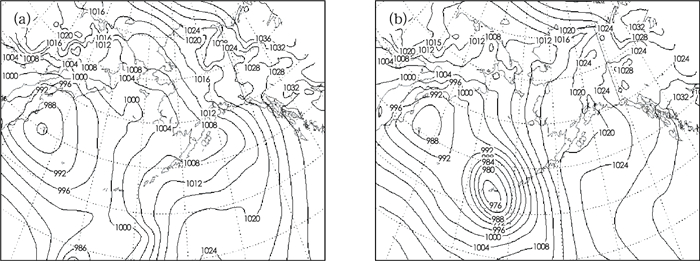
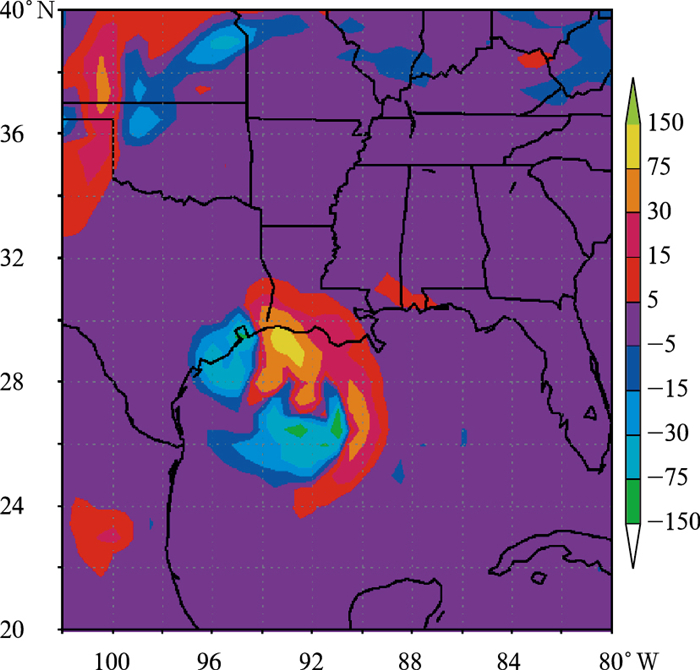
由于其高度的非线性特征,天气、气候、水文预报中所用的数值模式是混沌系统。也就是说起初很微小的不同(不能确定的误差)可能会随模式的时间积分而不断放大,致使二个预报结果变得完全不同[7-8]。其不同程度可以大到相当于从过去历史的预报场中随机抽样一般。这时模式的预报达到了上限(可预报极限)。再进一步的预报就没有什么意义了。这就是所谓的可预报性问题。这种在初值上或物理、模式处理中的微小差异而导致完全不同的预报结果在业务数值预报中特别是在重大天气事件预报中并不少见。因为重大天气事件经常同不稳定的大气状态相连,而在“不稳定”的状态下,轻微的不同推力可以导致物体产生完全不一样的运动(如图 1所示)。图 2、图 3是美国气象局的业务数值预报的实例。图 2是美国国家环境预报中心(NCEP)全球预报系统(GFS)模式所做出的两个500 hPa高度场的16天预报。这两个预报的差别仅仅是它们的起报时间相差6小时。但如图所示,它们的预报结果却相差十万八千里:一个预报大槽在美国东海岸(图 2a),而另一个在美国西海岸(图 2b),两者之差有3000多千米之遥。如果说这是因为预报时间较长(16天)的话,那么这种类似情形也可同样发生在短期预报中。图 3是NCEP短期集合预报系统(SREF)[9]中由区域模式Eta[10]所报的两个集合成员(mem 4 and mem 5) 2.5天的海平面气压场。此两成员之间的差异仅仅是它们初值有些微小不同(限制在初值误差估计范围之内),但结果却大相径庭:在相同的区域, mem 4(图 3b)预报为强气旋(中心气压低于976 hPa),而mem 5(图 3a)却是高压脊(约1008 hPa)。同样, 在模式的物理处理上微小的差异也可能导致很不一样的预报结果。作者在NCEP业务区域谱模式(RSM)[11]对对流参数化方案,在合理的误差范围之内增加了一项随机扰动(与时间倾向项成正比, 符合正态分布),并对2009年发生在墨西哥湾登陆美国的IKE飓风进行了试验,结果发现加与不加随机扰动对台风降水预报影响巨大。2天之后,两者24小时累计雨量预报之差达100 mm之巨(图 4)。如有兴趣的读者可以自己从NCEP业务的SREF集合预报网站(http://www.emc.ncep.noaa.gov/mmb/SREF/SREF.html)中观察这种不同集合成员间预报差异在每天实时预报中出现的情况。
|
图 1 “稳定”与“不稳定”状态的简单图示 Fig. 1 Schematic demonstration of "stable" and "unstable" situations |
|
图 2 NCEP GFS所做出的两个500 hPa高度场的16天预报 (a)为GFS模式预报的2006年10月19日00世界时的结果(起报时间为10月3日00世界时); 而(b)为GFS模式预报的2006年10月19日06世界时的结果(起报时间为10月3日06世界时) Fig. 2 Two consecutive 16-day 500 hPa HGT/VORT forecasts from NCEP Global Forecasting System (GFS), initiated 6 hours apart, respectively: (a) initiated at 00 Z, October 3 and verified at 00 Z, October 19, 2006; and (b) initiated at 06 Z, October 3 and verified at 06 Z, October 19, 2006 |
|
图 3 NCEP SREF二个Eta成员(mem 4和mem 5) 给出的63小时海平面气压预报 (起报时间为2007年1月10日09世界时,预报时间为1月13日的00世界时)。Mem 4(b)和mem 5(a)之间的差异仅在于它的起始初值有一些很微小的差异 Fig. 3 Two NCEP SREF Eta-member (mem 4 and mem 5) 2.5-day sea-level pressure forecasts initiated with slightly different initial conditions. Both forecasts were initiated at 09 Z, January 10 and verified at 00 Z, January 13, 2007 |
|
图 4 针对登陆美国的飓风IKE,用NCEP RSM模式所作的两个24小时累计降雨量的预报值之差 两者差异的产生在于其中一个预报的对流参数化方案中加入了一项与时间倾向项成正比的随机强迫项(服从正态分布)。预报的时间为48小时(2天) Fig. 4 The difference of 24 h-accumulated precipitation amount between two 2-day NCEP RSM forecasts during the landfall of Hurricane IKE over Gulf of Mexico in September 2009 (initiated at 09 Z, September 11 and verified at 09 Z, September 13, 2009) due to stochastic forcing. A random stochastic forcing term (proportional to tendency term and following a normal distribution) was added to the model's convective parameterization scheme (Simplified Alakawa-Shubert Scheme) in one of the forecasts |
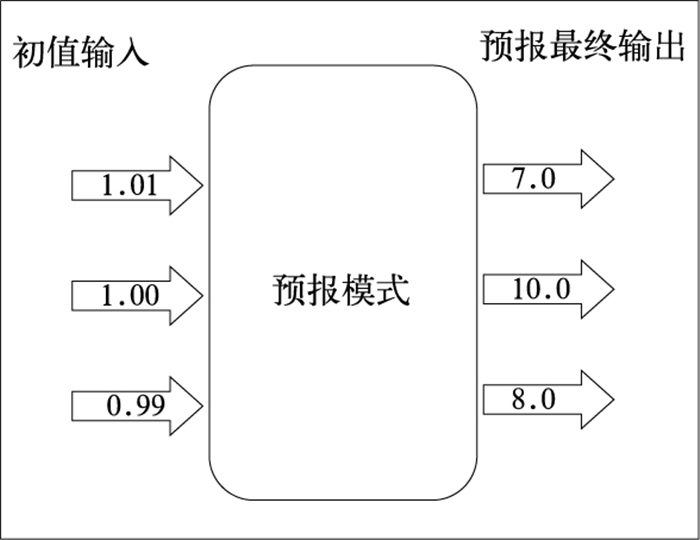
考虑到这些微小的起初误差是永远都无法避免的,可见目前单一值决定论预报存在很大的不确定性,有时预报正确,有时预报错误。既然初始时刻这些微小误差是不可避免的或不可知的,那么初值就不应该是一个而应该是一个在合理范围内的分布(众多初值)。我们也应该有理由相信所有这众多合理的初值所导致的众多的预报结果也都同样可信,而没有理由偏爱其中某一个预报(即单个决定论预报)。这可用以下简单的图例(图 5) 来说明。如果我们知道初值的误差范围为0.01,那么对于“观测值” 1.0来说,任何介于1.01和0.99之间的值都有同样的几率为真值。也就是说任何介于0.99和1.01之间的值都可以作为模式合理的初值。介于0.99~1.01之间的初值有无穷多,但在实际计算中我们不可能取无穷多的初值而只能选取其中的一些典型值或有效值来计算。这就是集合预报初值扰动的选取问题[12-15](注意:正是因为集合预报把一个“无限”的问题变成了“有限”的问题,集合预报只是一种在实际情形下可行的处理预报不确定性的变通办法)。譬如我们选取1.01、1.0和0.99为初值。如果1.01作为初值的预报值为7,1.0做初值的为10,0.99做初值的为8,那么7、10、8三者都应该是同样可信的预报值。这样做我们才有可能保证实况不至于被漏报。这就是我们为什么要做集合预报的原因。
|
图 5 集合预报的简单概念图示——由初值的不确定性导致的预报不确定性 Fig. 5 A schematic example about simplified conceptual forecast uncertainty issue due to uncertainties in initial conditions |
集合数值预报是单一决定论预报向多值的概率论预报转变的关键技术基础[12-17]。当然,用统计的办法也可以产生概率预报[18]。但是统计办法有其不可弥补的缺陷,那就是它反映的仅仅是过去出现过的一般状态而不能反映当时正在出现的和将来可能会出现的个别情况。我们知道,数值预报除了系统性的误差外,更重要的是随时随地随天气系统在变的随机误差。统计的办法可以用来消除系统性的误差, 但对随机误差却无能为力。这些随机性的误差就是数值集合预报要处理的对象[12],也是天气预报难报和经常出错的地方。
一般而言,单一决定论预报可用公式(1) 表示:
| $ X = {X_m} $ | (1) |
这里X代表实际情况,Xm代表预报。当然,公式(1) 也是我们作为科学家的梦想,希望实况能100%准确地被预报出来,然而,不尽人意的是实际情况往往是公式(2) 的情形,
| $ X = {\rm{ }}{X_m} + {X_o} $ | (2) |
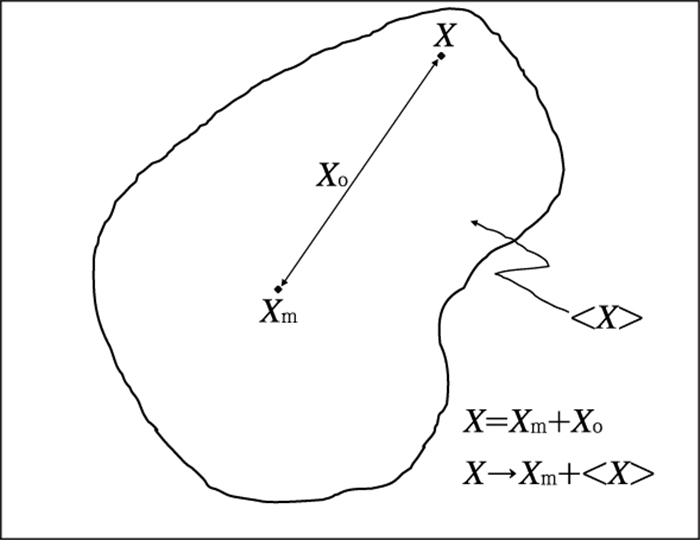
这里Xo是误差, 并且Xo的确切值在事先往往是不可知的!既然找不到Xo, 那么我们能否退一步?即能否找到一个不确定性的范围或分布<X>, 而希望这一范围<X>能包含这不可知的误差Xo, 这样实况就能被确包在Xm+<X>之中(公式(3) 和图 6), 即
| $ X \in {X_m} + < X > $ | (3) |
|
图 6 由集合预报提供的预报范围Xm+<Xo>。这里X为实况; Xm可视为集合平均预报; <X>(影区)为预报不确定范围; Xo是单一值预报的误差 Fig. 6 A schematic diagram of ensemble-based forecast Xm+ < X >, where Xm can be viewed as ensemble mean, < X > (shaded area) uncertainty range or distribution, and Xo forecast error of a deterministic forecast such as ensemble mean forecast |
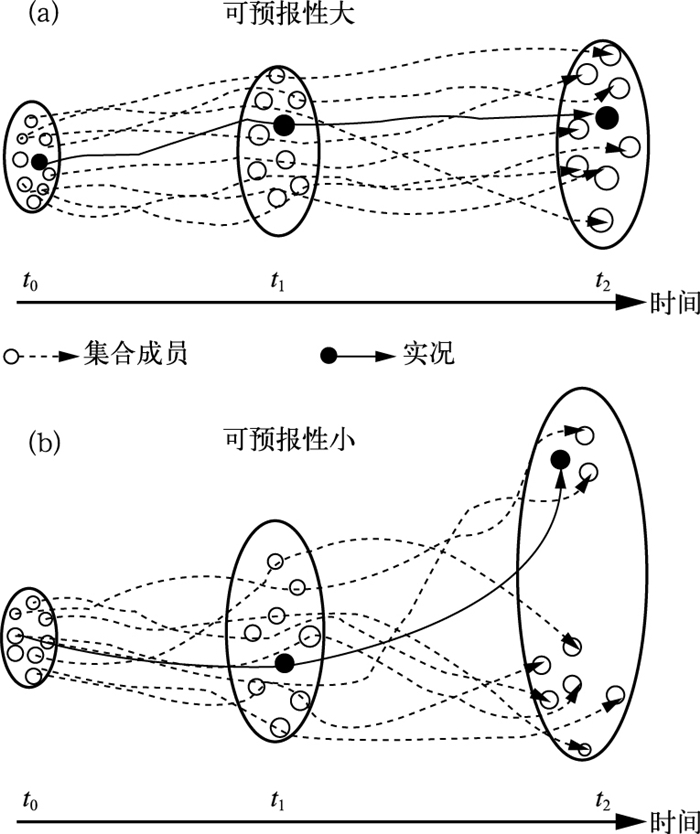
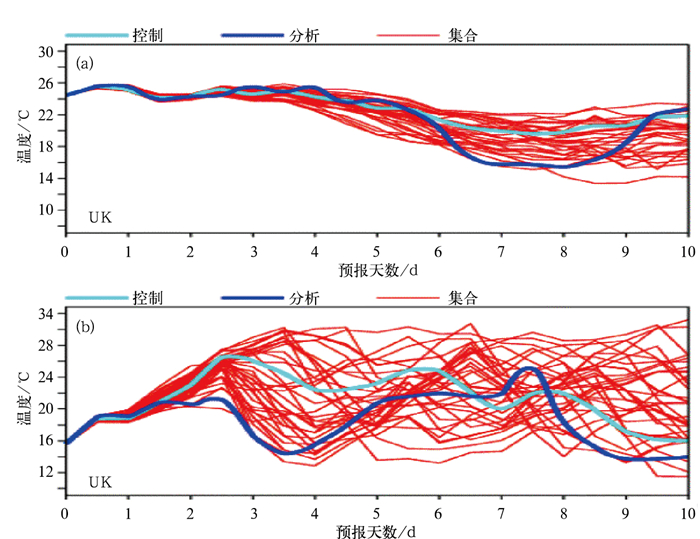
从而天气预报的任务就从公式(1) 转变为公式(3)。注意公式(3) 并不是“等式”而是“包含式”, 即实况X被包含在Xm+<X>之中。<X>可用统计的或动力的办法来产生。但如上所述,用统计的办法产生的<X>是“死”的; 而用动力的数值集合预报方法来产生的<X>是“活”的。也就是说当大气系统简单稳定,天气较好预报时,这一不确定范围<X>就比较小(即集合预报成员间很靠近, 图 7a);反之,就较大(集合预报成员间很疏远, 图 7b)。所以<X>的大小就定量地表示了某一特定预报的可信度。图 8就是一个很好的基于欧洲中心(ECMWF)中期全球集合预报系统的10天气温预报实例:图 8a说明1995年6月26日给出的伦敦地面气温预报很可信,因为集合成员(红色)都紧靠在一起。事后证明1~6天的控制预报(青色)同实况分析值(蓝色)很接近;而图 8b则说明1994年6月26日给出的伦敦地面气温预报却很不可信,因为集合成员(红色)间的离散度很大。事后也看到仅仅一天半之后,其控制预报(青色)同实况(蓝色)就相差很远了。其实公式(3) 就是集合预报的基本精神和思路。由此可见,集合预报的核心任务就是要定量准确地估计这一同大气的可预报性相联的、随机的、随时随地随天气系统而变的“预报不确定性”的范围或分布<X>,以确保实况被包含在所预报的范围之内。换言之,集合预报的重任是估计预报的随机误差的分布而非预报值本身。图 9是另一个基于集合预报的某地风向和风速预报的例子,它也展示了风向和风速随时间演变的不确定度。并且,这种同时表达风向和风速预报不确定性的方法也值得我们在业务预报实践中效仿。
|
图 7 用集合预报成员间的离散度大小来表征大气的可预报性或预报的可信度 (a)大气可预报性大,预报的可信度高;(b)大气的可预报性小,预报的可信度低。横坐标表示预报时间,t0是起报时间,t2是终报时间,t1是t0与t2之间的任何时间,虚线表示每个集合预报成员的时间演变,实线表示实况。此图引自文献[19] Fig. 7 The spread among ensemble member forecasts used to measure degree of predictability or confidence level of a forecast: (a) is a more predictable or high confident forecast and (b) a less predictable or low confident one. The abscissa denotes forecast time where t0 is initial time, t2 final time, and t1 any time between t0 and t2. The dash trajectories represent the time evolution of each ensemble members and the solid one the assumed truth (from [19]) |
|
图 8 欧洲中期数值天气预报中心(ECMWF)中期全球集合预报系统所做的英国伦敦地面气温的10天预报 (a)是可信度高的预报(起报时间为1994年6月26日);(b)是可信度低的预报(起报时间为1994年6月26日)。红色代表集合预报成员,青色为高精度的控制预报,而蓝色为实况分析值。横轴是预报时间(天数),纵轴是温度(℃) Fig. 8 10-day surface air temperature forecasts from ECMWF medium-range ensemble prediction system for London, UK. (a) a high confident case (initiated from June 26, 1995); (b) a low confident one (initiated from a same date but in a different year, June 26, 1994). The Red is for the ensemble members, the Cyan for the higher-resolution control forecast, and the Blue for the analysis. The horizontal axis represents forecast time (d) and the vertical axis temperature (℃) |
|
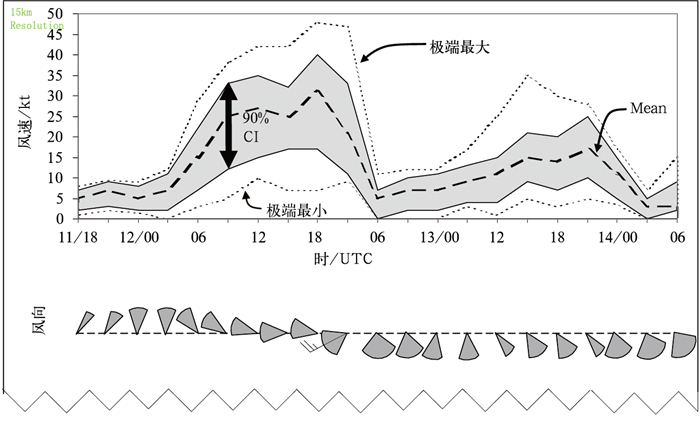
图 9 日本Misawa空军基地基于美国空军气象局的联合中尺度集合预报系统的60小时地面风的预报 (a)中间的粗断线是集合平均风速(节),阴影区为90%置信度的可能性风速范围,上下外围两侧的细断线则表示最大或最小的可能风速。(b)阴影三角区为风向的不确定性范围,阴影区的中间为集合平均风向。这随预报时间而变化的风向和风速预报的不确定性清晰可见(此图由Dr. F. Anthony Eckel提供,特此致谢) Fig. 9 2.5-day surface wind forecast at Misawa Air Force Base, Japan, initiated at 18 Z, November 11, 2006. The range of possible wind speeds is given with a 90% confidence interval (shaded) and extreme maximum and minimum (dotted) together with ensemble mean value (thick broken line). Wind direction uncertainty and prevailing (mean) direction are also plotted at the bottom. The forecast was derived from the US Air Force Weather Agency's Joint Mesoscale Ensemble system (courtesy of Maj. F. Anthony Eckel) |
关于集合预报常会有以下一些误解。第一,人们总是想通过各种各样所谓“集成”的办法[20]试图找出一个最佳的单一值预报,就是想把公式(3) 再从“包含式”还原为“等式”。当然,通过对所有集合成员的有用信息经过综合集成处理(如集合平均和中值预报)确实会在统计意义上提高单一值预报的准确率[21-22],但这只是集合预报技术的一个次要功用而不是集合预报的主要目的。况且集成的单一值预报(如集合平均和中值预报)有较好的预报水平是指平均意义上的,而并不能保证每次都如此。并且它还会有不可避免的误差,特别是在大气特别不稳定的分岔关头(即有双态或多态出现的可能性时),集成的单一值预报往往会完全漏报实况。这对于许多用户而言,这些集成的单一值预报不仅不会给决策带来益处,反而是带来害处[5]。所以,如上所述,集合预报的主要目的并不是要报一个更准确的单一值,而是要报预报误差的可能分布, 这样才能保证实况不被漏报。
第二,似乎刚好同以上的误解相反,有人担心用了集合预报就没有了单一值的预报。显然实际情况是,集合预报不但仍可提供单一值预报,而且往往是在平均意义上更准确的预报, 如Zhou和Du的最近研究表明集合预报能大大地提高中国东部地区雾的预报水平[22]。
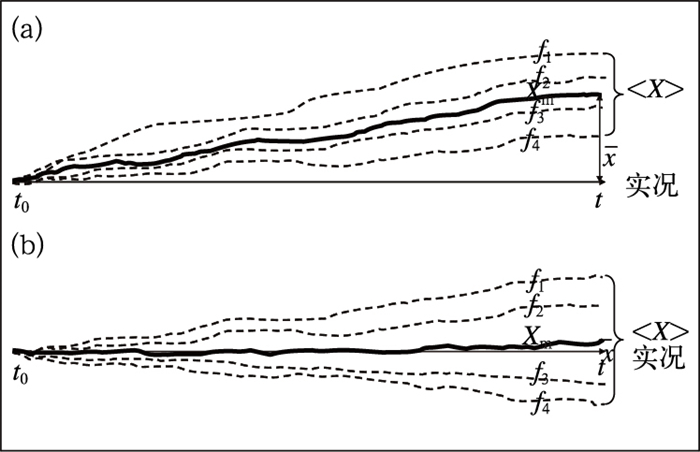
第三,人们经常把集合预报作为一种独立的技术来讨论。如有人以为集合预报是万能的,有了它就可以提高预报水平而忽视模式和同化的发展;而当漏报时,则认为该集合预报系统不好,如此等等。其实在公式(3) 中Xm可视为集合成员的平均预报,而它的准确与否主要取决于模式的能力和初值的质量;而公式(3) 中<X>的质量才是取决于集合预报技术的优劣。所以如果一个模式和初值没有能力和信息来预报某一天气现象,那么再高明的集合预报技术也是无能为力的。具体来说,对于一个基于单模式单物理的集合预报系统而言,虽然它通过集合平均能消除随机性误差而得到一个从统计意义上来说比较准确的解(图 10b), 但它是没有能力来消除预报的系统性误差的(图 10a)。如图 10a所示, 因为系统性偏差是由模式和资料的质量造成的,所以集合预报中的每个成员都有此系统性的漂移, 因此集合平均无法消除系统性的误差。而当系统性误差去除后,集合预报的效果就会大大地得到加强[23-24]。当然, 基于多模式或多物理的集合预报系统,由于不同成员可能有不同的系统性偏差,所以集合平均有可能部分消除预报的系统性误差。简言之,集合预报技术的发展不能同模式和资料同化技术的发展分开, 它们应该是相辅相成的。好的模式和资料是好的集合预报系统的基础,而好的集合预报系统能更好地使该模式和资料发挥更大的作用。
|
图 10 基于单模式单物理集合预报系统的成员预报(f1, f2, f3, f4)的系统性漂移图示 水平轴代表实况,X是模式的系统性误差,它是模式和资料的质量造成的,而与集合预报技术无关; <X>是随机分布的预报不确定性范围,它同集合预报技术有关; Xm是集合平均预报(实线)。(a)系统性误差大; (b)系统性误差小 Fig. 10 Illustration of "systematic model bias" and "random forecast uncertainty" in a "single-model and single-physics" based ensemble prediction system (a) with large model bias and (b) with little model bias The abscissa represents "truth" where t0 is initial time and t final forecast time; the dash curves each ensemble members (f1, f2, f3, f4); the solid curve ensemble mean forecast (Xm); X model's systematic bias attributed by the quality of model and initial conditions; and < X > random forecast uncertainty attributed by ensemble techniques used |
最后,同上面第三点相反, 有人认为“现在单个预报模式还没有搞好,没有必要做集合预报。”从表面上来看,此话似乎有一定道理,但其实可能刚好相反。确实,从上一点的讨论中我们知道一个好的集合预报系统应该建立在一个好的模式系统基础上。所以,如果现有的模式没有一丁点儿的预报技巧,那么在此基础上做集合预报确实是“巧妇难为无米之炊”——不可能,因为“垃圾+垃圾=垃圾”。但是,如果模式已具备基本的预报能力(作为业务预报用的模式应该具备这种能力)而只是有时对有时错,其预报误差较大的话,那么为了更好地服务公众和用户,我们就更应该用集合预报的方法来估计它的预报不确定性而不应该轻易地相信其单一值预报。否则,单凭其单一值输出作为业务指导预报将会经常误导公众和用户。要知道正是因为单一值预报有误差,这才是我们需要做集合预报的根本原因。如果有一天,单一值预报没有了误差,那么集合预报也就不需要了(当然这一天永远也不会到来,因为误差源总是存在——见第一节讨论)。作者多年的研究和实践经验表明,其实对于愈难预报的量,通过简单的集合处理(如平均和中值预报),其预报水平的提高也愈明显。文献[22]就是一个很好的例子:目前的数值模式对雾的预报水平非常低,但也正因为如此,通过集合预报技术对雾的预报水平的提高也就特别的明显。因此,认为“现在单个模式预报水平还不够好而不应该做集合预报”的想法是大错特错的,并且是对气象服务有害的。当然,对于一个基于不太好的模式系统为基础的集合预报系统,我们应该在技术上重视以下三个方面。第一,要明白自己的基础不好,所以应该花大力气改进模式和提高初值质量以增加预报的信息量,从而提高预报的应用价值。第二,不好的模式所做的预报其系统性的漂移可能也较大。而从上面的讨论(图 10a)知道,集合预报其实对模式的系统性漂移无能为力,所以在生成最后的集合预报产品以前,预报的后处理(如漂移的订正)要特别加强。最后,由于不好的模式系统所产生的预报其随机误差(正是集合预报需要处理的对象)可能也较大,所以为了使集合系统所估计的预报范围能确保实况被包含在其中,集合成员间的离散度就要足够大。这意味着对初值和物理的扰动方法的要求较高,甚至要求初始扰动的幅度虚假地大一些;并且成员数也应该较多,特别是多模式和多物理(加初值扰动)的集合其效果更佳。这原因是因为“部分真理+部分真理=比较全面的真理”。显然,上述讨论并不是说当模式和初值足够好时,就不需要集合预报了。因为从第一节讨论中知道导致天气预报有可预报性限制的误差源永远都将存在,所以预报的不确定性也将永远存在并且在重要关头时还会很大。但这两种情形的区别在于,当模式系统不好时,预报的不准确性不仅仅是“可预报性的问题”所致,这时改进模式和初值以及后续订正等都会大大地减小预报的不确定性。所以这时应该实行“双轨制”(改进模式系统和集合预报)来共同提高预报的应用价值。而当有一天模式和初值已达到了几乎“完美”的水平,这时预报的不准确性将主要是“可预报性的问题”所致。因为那时改进模式系统的余地已不大,所以“集合预报”的“单轨制”可能是唯一可用来有效提高预报应用价值的途径。
4 数值预报的新纪元如果集合预报的目的只是为了改进单一值决定论预报的质量的话,那么它仅仅是数值预报发展史上众多方法中的又一种改进的方法而已。然而,从第2节的讨论中我们知道集合预报的主要目的是定量估计预报的不确定性范围。因此,它不仅仅是一种新的技术而更重要的是为数值预报开创了一个新的纪元。其主要特征指标有二个。
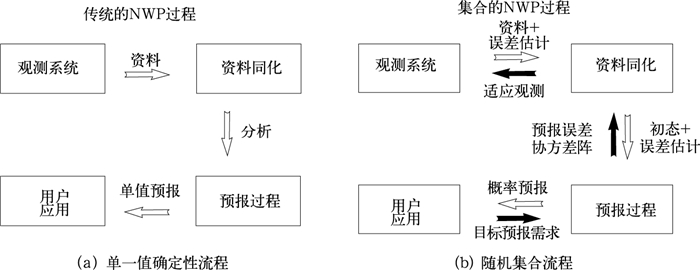
第一个特征是从单一值的确定论向多值的概率分布转变。这一转变不仅仅只在预报层面上,而包括整个数值预报系统中的所有环节(图 11)。观测资料除了平均观测值之外,还应有相应的误差范围估计;资料同化步骤中输出的分析资料也不再是一个而是一群(集合)分析资料,以反映初值的不确定性;预报就是本文所讲的集合预报,以反映预报的不确定性;预报产品由单一值预报变成多值的概率预报;用户决策所用的气象信息不再由预报员替他们来选择,而是各用户根据自身对气象条件的依赖程度来决择(这将在另文阐述[5]),总之,每一步都不再是单一值的决定论,而是包含了不确定性的定量估计(概率密度函数)(图 11b)。
|
图 11 数值预报系统的理念。(a)为传统的基于单一值确定论思想的流程图,它是单值的和单向的;(b)为基于考虑了不确定性的概率论思想的流程图,它是多值的和双向互动的 Fig. 11 Paradigm shift of numerical weather prediction (NWP) system. (a) traditional 1-way single-value deterministic system; (b) new interactive (2-way) probability density function (PDF) based system |
第二个特征就是从单向过程变为双向过程。目前传统的数值预报流程是单向进行的(图 11a), 即观测→资料同化→模式预报→用户应用, 而没有反向反馈。但以集合预报为中心技术的新数值预报系统中,后面的步骤可以修正前面的步骤(图 11b), 譬如用户的应用可以改变观测的步骤。用户或预报员从集合预报的离散度可以判断所关心的重大天气系统的预报的不确定性是否过大。如是, 那么为了减少预报的不确定性以满足服务的需要,气象专家可以应用相关技术在上游地区追踪该预报不确定性的可能来源,然后在该源头区进行一些特殊的加密观测以期提高作为模式初值用的分析资料的质量。这样希望下一时刻作出的数值集合预报的不确定性会大大减小,并提高预报的精度。这就是所谓的目标观测或适应观测的概念[25-26]。类似地,在天气稳定较易预报的情况下,则可以减少应用上游的观测资料(如卫星、雷达等大量的遥感资料)以节省资源。集合预报和资料同化过程也互相依赖和影响而成为一体化:集合预报所估计的不确定性为资料同化提供背景误差信息,而反过来“集合”资料同化则为集合预报各成员提供众多不同的初值场[27]。
5 预报员的新使命随着数值模式的不断改进和初值质量的不断提高,预报员的头脑推理将越来越比不过模式的结果。靠人脑和经验订正模式预报的余地将愈来愈小。所以,在只发布单一值决定论预报的情形下,预报员最终将变成“转播员”而已。然而,在用集合预报定量考虑预报的不确定性而发布多值的概率预报的情形下,预报员的作用就将不是那么单纯的“转播”了。
首先,预报员要根据集合预报成员间的离散度大小来发现自己面临的“当天的预报问题”是什么,即哪里和哪些天气系统或要素不确定性很大、较难预报(发现问题)。有时,即使一个大的天气系统如气旋并不难报,但在该同一大系统下的不同要素或不同部位的预报的可信度经常很不一样。如在强气旋区域,可能大风的预报很有把握,但是降水的落区和量级的预报却不太可信。又如在靠近气旋中心地区预报的可信度较高,而在接近外围边缘地区的预报却经常不可靠。类似这些不确定性在集合预报中都会有很好的定量反映。所以,预报员首先要把它们找出来,把注意力集中到这些不好预报的方面上去。接下来,再从气象的角度去找出“为什么具有那么大不确定性的原因”(寻找原因)。譬如,某地气温不好报的原因可能是刚好位于冷锋附近,如冷锋过境则很冷,反之则较暖和。而模式预报的该冷锋明天的位置不确定性很大。又如,某地明天风向预报的不确定性非常大(可以完全相反,即相差180°),而其原因是该地可能会处于气旋的不同部位,因为气旋的位置预报具有很大的不确定性(即不同集合成员间差距很大),如此等等。作为预报员,要把这些原因找出来并用浅显的语言告知公众和用户,使他们了解为什么明天某预报的不确定性很大或可信度很小而不要轻易相信某个特定的结论而应做好多手准备。相信有了这些合理的解释和适当的忠告之后,用户是会逐步理解和接受预报的不确定性的,从而减少对气象部门的一味责怪。(在这方面,我们应该向医学界学习,医生通常会实事求是地告诉病人某手术或治疗方案的成功率是多少,而病人并不因此而责怪医生。所以,可以这样推论,公众对气象预报的指责有一部分原因是由于我们自己的成功所导致的。那些过去的成功使我们自信我们能够每次成功而不再言失败的可能性,从而误导了公众今天对天气预报的高期望)。
最后,预报员在正式对外公布预报之前,可以结合其他新的资料和他们丰富的实践经验来找寻一些有用的信息,也许可以“尽量减小一些集合预报所反映的该预报的不确定度”(减小不确定性)。当然,对于一个基于“可靠的” [5]集合预报系统上的概率预报,预报员能否科学地、有意义地调整其概率是一个尚待检验的课题。因为我们知道对于系统性的误差(反映在概率分布的均值上),人的经验经常有能力来修正它的一部分,但对于随机误差分布(反映在概率相对其均值的分布状态上),人的经验是否也有能力来修正它并不太清楚,要有待今后进一步研究。另外,如前节所述,新的预报体系是一个双向系统,所以,如果预报员发现某个天气系统的预报不确定性非常大,而相应的天气事件又很重要,那么他可以把意见反馈给国家数值预报中心并要求实施相关的目标观测,以期望下一时刻的集合预报所给出的预报不确定性会减小,预报质量会提高。这种要求进行特殊的目标观测的做法,已在美国气象局的日常业务运作中进行了许多年[26](http://www.emc.ncep.noaa.gov/gmb/targobs/index_files/wsr.htm)。
综上所述,“单一值决定论预报时代”将最终使预报员的职责退化为简单的“转播员”。而“多值的集合预报时代”将使预报员的职责更具挑战性和多样性,这包括了上面所讨论的三大新任务——“发现问题”、“寻找原因”和“减小不确定性”。
6 小结本文试图用浅显的语言讨论数值集合预报这一科学题目。由于大气系统的非线性和复杂性,加上初值和模式等本身无法避免的一些不确定性,使得单一值的决定论预报无法避免失误,特别在重要天气出现时更是可能如此。许多例子让我们看到数值预报对初值和物理的不确定性非常敏感。因此,我们需要用集合预报来尽量避免漏报重大的天气现象。集合预报的中心任务就是要定量估计预报不确定性的分布以确保实况不会超出所预报的范围,而不是目前很多人以为的去改进现有的单一值决定论预报的质量(虽然可以这样做,并且现在也经常这样做, 将来还会继续做)。当然这样一来,用户将面临如何来处理预报上不确定性这一难题。关于如何应用含有不确定性的概率预报来决策以及概率预报是否比单一值决定论预报更有价值等等这些问题将在另文讨论[5]。
文章也强调指出集合预报技术的发展不能同模式和资料同化技术的发展分开, 它们应该是相辅相成的。好的模式和资料是好的集合预报系统的基础,而好的集合预报系统能更好地使该模式和资料发挥更大的作用。从气象服务的角度来看,对于已具备基本预报能力但预报误差比较大的不太好的业务运行模式系统,其配套的集合预报系统的建立尤显重要,因为它的单一值决定论预报很不可信,而没有什么应用价值。而这时集合预报技术却往往能显著地提高预报效果。在这种情况中,多模式和多物理的集合系统往往更具效果并且预报的后续订正也非常重要以弥补模式系统本身的缺陷。当有一天模式和初值几近“完美”时,预报的问题将主要是“可预报性”的问题,那时“集合预报”可能是唯一可用来有效提高预报应用价值的途径。
集合预报并不仅仅是一种新的技术和方法, 而它的方法和理念将使整个数值预报体系进入一个新的纪元。这一新纪元的特征指标有二方面:一方面是在观测、资料同化分析、预报、产品制作和用户应用决策等各个环节都从单一值的确定论转变为多值的概率分布; 另一方面是这些环节的流程由单向转变为双向互动的过程。最后, 在“集合预报时代”,预报员的职责将更具挑战性和多样性。预报员将面临可能的三大新任务——(1) 去发现自己面临的“当天的预报问题”是什么,即确认何类天气系统或现象具有很大的预报不确定性(发现问题);(2)“找出该预报不确定的原因是什么”并在发布预报时向公众和用户做出合理的解释和适当的忠告(寻找原因);(3) 利用新资料、经验和新技术尽量减小预报的不确定度(减小不确定性),最大程度地提高预报的应用价值。
杜钧, 陈静, 2010. 天气预报的公众评价与发布形式的变革[J]. 气象, 36(1): 1-6. DOI:10.11676/qxxb2010.001 |
U.S. National Research Council, 2006. Completing the forecast: characterizing and communicating uncertainty for better decision using weather and climate forecasts[M].
Washington DC: The National Academy Press.
|
Lorenz E N. 混沌的本质[M], 刘式达, 刘式适, 严中伟译. 北京: 气象出版社, 1997.
|
丑纪范, 2002. 大气科学中的非线性和复杂性[M]. 北京: 气象出版社.
|
杜钧, 邓国. 单一值预报向概率预报转变的价值: 谈谈概率预报的检验和应用[J]. 气象, 待发表.
|
王东海, 杜钧, 柳崇健. 正确认识和对待天气预报的不确定性[J]. 气象, 待发表.
|
Lorenz E N, 1963. Deterministic nonperiodic flow[J]. J Atmos Sci, 20: 130-141. DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 |
Lorenz E N, 1965. A study of the predictability of a 28-variable atmospheric model[J]. Tellus, 17: 321-333. |
Du J, DiMego G, Toth Z, et al. NCEP short-range ensemble forecast (SREF) system upgrade in 2009[C]. American Meteorological Society 19th Conference on Numerical Weather Prediction, 2009, 4A.4, [available online at http://www.emc.ncep.noaa.gov/mmb/SREF/reference.html]
|
Rogers E, Black T, Deaven D, et al, 1996. Changes to the operational "early" Eta analysis/forecast system at the National Canters for Environmental Prediction[J]. Weather and Forecasting, 11: 391-413. DOI:10.1175/1520-0434(1996)011<0391:CTTOEA>2.0.CO;2 |
Juang H-M H, Hong S-Y, Kanamitsu M, 1997. The NCEP regional spectral model: An update[J]. Bulletin Amer Meteoro Soc, 78: 2125-2143. DOI:10.1175/1520-0477(1997)078<2125:TNRSMA>2.0.CO;2 |
杜钧, 2002. 集合预报的现状和前景[J]. 应用气象学报, 13(1): 16-28. |
李俊, 杜钧, 王明欢, 等, 2009. 中尺度暴雨集合预报系统研究中的初值实验[J]. 高原气象, 28(6): 1365-1375. |
陈静, 薛纪善, 颜宏, 2005. 一种新型的中尺度暴雨集合预报初值扰动方法研究[J]. 大气科学, 29(5): 717-726. |
Mu M, Zhang Z, 2006. Conditional nonlinear optimal perturbations of a two-dimensional quasi-geostrophic model[J]. J Atmos Sci, 63: 1587-1604. DOI:10.1175/JAS3703.1 |
李泽椿, 陈德辉, 2002. 国家气象中心集合数值预报业务系统的发展及应用[J]. 应用气象学报, 13(1): 1-15. |
陈静, 陈德辉, 颜宏, 2002. 集合数值预报的发展与研究进展[J]. 应用气象学报, 13(4): 497-507. |
Wilks D S, 2005. Statistical methods in the atmospheric sciences[M].
New York: Academic Press, 627.
|
Du J. Short-range ensemble forecasting of an explosive cyclogenesis with a limited-area model[M]. Ph.D. Dissertation, University of Arizona, 1996:146[available from UMI Dissertation Service, 300 N. Zeeb Rd., P.O. Box 1346, Ann Arbor, MI, 48106].
|
杞明辉, 许美玲, 程建刚, 等, 2006. 天气预报集成技术和方法应用研究[M]. 北京: 气象出版社, 189.
|
Du J, Mullen S L, Sanders F, 1997. Short-range ensemble forecasting of quantitative precipitation[J]. Mon Wea Rev, 125: 2427-2459. DOI:10.1175/1520-0493(1997)125<2427:SREFOQ>2.0.CO;2 |
Zhou B, Du J, 2010. Fog prediction from a multimodel mesoscale ensemble prediction system[J]. Weather and Forecasting, 25: 303-322. DOI:10.1175/2009WAF2222289.1 |
Du J, Mullen S L, Sanders F, 2000. Removal of distortion error from an ensemble forecast[J]. Mon Wea Rew, 128: 3347-3351. DOI:10.1175/1520-0493(2000)128<3347:RODEFA>2.0.CO;2 |
马清, 龚建东, 李莉, 等, 2008. 超级集合预报的误差订正与集成研究[J]. 气象, 34(3): 42-48. DOI:10.7519/j.issn.1000-0526.2008.03.007 |
Du J, Yu R, Cui C, et al. Interactive prediction-observation system to possibly increase predictability of heavy rain forecasts by using mesoscale ensemble: a simulation study. Fourth International Ocean-Atmosphere Conference[C]. 2007, 11.
|
Szunyogh I, Toth Z, Zimin A, et al, 2002. Propagation of the effect of targeted observations: The 2000 winter storm reconnaissance program[J]. Mon Wea Rev, 130: 1144-1165. DOI:10.1175/1520-0493(2002)130<1144:POTEOT>2.0.CO;2 |
Hamill T M, 2006. Ensemble-based atmospheric data assimilation. Chapter 6 of Predictability of Weather and Climate[M].
London: Cambridge Press, 718.
|
 2010, Vol. 36
2010, Vol. 36 