引言

20世纪70年代以来，国内外雷达气象学者在用雷达探测强对流天气领域做了大量的工作，他们分析了风暴发生、发展、成熟和消亡的物理机制，提出了一些风暴算法，其中，1982年Austin等^[1]提出了三维矩心算法，即把每一个风暴单体看作是一个具有三维连续结构的整体，计算相关物理特征量，预报时采用外推技术。经Rosenfeld^[2]，Michael等^[3]对这一方法进行改进后，该算法在全美NEXRAD(WSR-88D Build 7.0) 业务系统中得到广泛应用，并取得了良好的效果；当然，用户在使用过程中反映当出现多个风暴相距较近、风暴移动不规则以及风暴出现了合并和分裂时，误差较大。鉴于此，1997年，Johnson等^[4]进一步提出利用7个反射率因子阈值来替代此前唯一的阈值，同时采取特征核抽取技术，并对空间相距较近的多个风暴单体进行合并或者删除处理，而且允许远距离上的2D(二维，下同)风暴单体存在，该算法被WSR-88D的Build 9.0所采用，同时该技术也被我国雷达所引进，在业务上进行了广泛的应用^[5-7]。

2006年，广州中心气象台自主研发了临近预报系统“SWIFT”，在这个系统中，风暴产品吸收了WSR-88D风暴系列算法的先进技术，并进行了一些改进，可以适用于多部雷达的区域拼图资料。2007年，SWIFT系统参加了北京奥运会天气预报示范项目的测试工作。本文将简要介绍SWIFT系统中风暴产品的设计及其在FDP测试期间的表现。

1 SWIFT系统中风暴产品的设计

2007年，在北京奥运会天气预报示范项目测试期间，北京气象服务中心能同步实时收集四部多普勒雷达基数据，分别是：北京两部(SA型和CC型)、天津(SA型)和石家庄(SA型)各一部。鉴于此，在SWIFT系统中，先对多部雷达进行实时拼图^[8]，然后应用风暴系列算法。由于北京有一部CC型号的雷达，因此在2007年FDP测试期间，只选择了北京、天津和石家庄三部同是SA型号的雷达基资料进行拼图，参与拼图之前，还对雷达资料进行了超折射回波的抑制处理^[9]；拼图覆盖范围达到了8个经度和6个纬度，拼图产品每6分钟更新。

1.1 风暴识别算法

SWIFT系统中的风暴产品在识别风暴^[10]时，借鉴了WSR-88D Build 9.0中的S CIT(Storm Cell Identification and Tracking)算法的设计理念，首先采用5个反射率因子阈值对拼图资料进行重复处理，对识别出的风暴段进行组合形成风暴分量，允许风暴分量重叠并按识别阈值分类保存。其次，对于重叠的风暴分量，采用了特征核抽取技术，以获取最大反射率因子阈值识别出的风暴分量，其余分量丢弃。再次，考虑到雷达测距限制，超过一定距离阈值的2D分量虽无与其垂直相关的分量，但仍可能是强风暴的一部分，予以保存，即允许远距离存在2D风暴。然后，将垂直方向上相距较近、水平投影重叠的上、下两单体进行合并。最后，考虑到采用多反射率因子阈值和核抽取技术之后，会识别出很多的风暴，为了保留主要追踪目标，避免多个距离相近的风暴造成匹配误差和视觉拥挤，系统还对相近单体做处理，即：若两单体质心相距小于距离阈值，且两者厚度之差超过一定阈值，则删去弱单体。

1.2 风暴追踪算法

对于当前时刻的风暴，还需要追寻前一时刻的位置，风暴追踪的基本思想是：在空间位置相关的前提下，按照最大相似原则进行匹配。当前时刻的风暴位置与前一时刻风暴的预报位置进行空间位置相关判断：

(1) 若当前时刻只有一个风暴体与前一时刻风暴的距离小于或等于相关的风暴最小距离阈值，且满足这两个风暴体的反射率因子权重体积的比值大于或等于相关的风暴最小体积比阈值，则将之匹配。

(2) 若当前时刻有多个风暴体与前一时刻风暴的距离小于或等于相关风暴最小距离阈值，则按以下原则进行处理。

如果当前时刻这几个风暴体的反射率因子权重体积之和与前一时刻该风暴体的反射率因子权重体积的比值大于或等于风暴分裂最小体积比阈值，则说明可能存在风暴分裂，就认为它们都与前一时刻该风暴相关。反之，则说明不可能存在风暴分裂现象，取前一时刻距该风暴距离最小的一个与之相匹配。

(3) 若当前时刻没有一个风暴与该风暴的距离小于或等于相关风暴最小距离阈值，则认为前一时刻的风暴已在当前时刻之前消亡。

(4) 若当前时刻的某一风暴在前一时刻有多个风暴与之相关，就认为发生风暴的合并。

(5) 若当前时刻的某一风暴在前一时刻没有与之相关的风暴体，则认为该风暴为新生的单体。

1.3 风暴预报算法

与WSR-88D中SCIT不同，文中利用TREC技术获取的回波运动矢量场来预报风暴的位置。

Rinehart^[11]首先发展TREC技术作为分析雷达回波移动之用，该方法对于稳定性降水系统反演效果较好；对于强对流系统，由于其回波生消频繁，效果相对差一些。文中沿用这一方法，对新一代多普勒天气雷达区域拼图输出产品，等分出相同大小的二维像素阵列，使用TREC技术，获取回波移动矢量^[12]。每个阵列，都会以阵列为中心定出一个搜索范围，在前一时刻的拼图反射率场中，寻找与其相关的阵列。相关系数R 是根据下面的公式计算：

$ \begin{align} &{{R}_{c}}= \\ &\frac{\sum\limits_{k}{{{\eta }_{1}}\left( k \right){{\eta }_{2}}\left( k \right)-\frac{1}{N}\sum\limits_{k}{{{\eta }_{1}}\left( k \right)\sum\limits_{k}{{{\eta }_{2}}\left( k \right)}}}}{[(\sum\limits_{k}{{{\eta }_{~}}{{_{1}}^{2}}\left( k \right)-N\cdot {{\overline{{{\eta }_{1}}}}^{2}})\times (\sum\limits_{k}{{{\eta }_{2}}^{2}\left( k \right)-N\cdot {{\overline{{{\eta }_{2}}}}^{2}}})}]} \\ \end{align} $

(1)

公式中的η₁和η₂代表两个时间中的二维像素阵列，N是阵列内的像素总和。

对于像素阵列大小的选择，按照Tuttle & Foote(1990) 的结论，并没有具体的规定，应根据监测目标的性质来确定。当然，如果阵列太大，TREC矢量场就只能反映较大范围的回波动向。每个阵列在上一时刻拼图反射率场中的搜索半径，选择与阵列的边长相同。为减少单从相关系数计算所引起的误差，每个TREC矢量值，首先会与附近的多个TREC矢量的平均值进行比较，若偏差多于25度，该矢量值会被平均值所取代，然后再进行整个TREC矢量场的客观分析。

在TREC矢量场客观分析中，每一个TREC值的分量会利用Cressman加权函数进行客观分析，从中得到较为平滑的TREC矢量分布。每次订正以网格点(i，j)作中心，根据扫描范围内各网格点与中心的距离，订出加权因子。假设s(i，j)为其中一个TREC矢量，s ₀(i，j)及s_n(i，j)分别代表其初估值与经过n次订正后得到的数值。订正值依照以下公式计算：

$ {{s}_{n}}\left( i, j \right)={{s}_{n-1}}\left( i, j \right)+\Delta {{s}_{n-1}}\left( i, j \right) $

(2)

其中，s_n-1(i, j)是经过n-1次订正得到的数值(n＝1，2，3，…)，而

$ \Delta {{s}_{n-1}}\left( i, j \right)=\frac{\sum\limits_{k}{w{{\left( i, j, k \right)}^{2}}\Delta {{s}_{n-1}}\left( k \right)\text{ }}}{\sum\limits_{k}{w\left( i, j, k \right)}} $

(3)

Δs(k)是位于扫描范围内第k个网格点上之误差，w(i, j, k)是Cressman加权函数：

$ w\left( i, j, k \right)=\left\{ \begin{align} &\frac{{{R}_{s}}^{2}-{{d}_{m}}^{2}}{{{R}_{s}}^{2}+{{d}_{m}}^{2}~}\ \ \ \ \ \ \ {{d}_{m}}{{~}^{2}}\le {{R}_{s}}^{2} \\ &0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{d}_{m}}^{2}>{{R}_{s}}^{2} \\ \end{align} \right. $

(4)

R_s为扫描范围半径，d_m是由第k点到扫描范围中心的距离。

在FDP测试期间，运用TREC技术处理3 km高度上的反射率因子拼图产品，获取3 km高度上的回波移动矢量。对于当前时刻识别出的每一个风暴，选择风暴中心点的TREC运动矢量，外推一个时次(6分钟)；当风暴外推到下一个时次时，选择新的风暴中心点的TREC运动矢量，继续外推；如果在风暴中心的预报位置处没有TREC运动矢量，则选择TREC矢量全局平均值，进行惯性外推；直至完成风暴1小时的预报。

2 风暴产品在“FDP”测试期间的应用 2.1 运行情况

2007年7月和8月，北京奥运会天气预报示范项目(FDP)进行了第二次测试。测试期间，北京出现了多次强对流过程，分别为：7月7日，7月17日，7月18日，7月30日，7月31日，8月1日，8月6日，8月7日，8月12日，8月25日和8月26日。在这些强对流个例中，既有系统性的，也有孤立的单体，且具有一定的样本数，因此能够对SWIFT中的风暴产品进行较为全面的检验。在测试期间，整个SWIFT系统的运行是稳定的。预报员在对强对流单体进行临近预报和预警时，风暴产品有着重要的参考价值，它可以与其他产品叠加显示，如：可以在3 km高度等高面(CAPPI)拼图产品上叠加TREC技术获取的回波运动矢量场，同时也叠加风暴产品。

7月30日夜间至31日凌晨，北京地区出现了剧烈的强对流天气，大量的强风暴单体成团成簇的排列在一起，回波区整体向北偏东方向移动。风暴识别算法较为准确地分离出大范围回波区内的每一个单体核(见图 1)，图中用圆圈表明当前时刻风暴的大小，而圆圈中心对应了当前时刻风暴的位置。风暴追踪算法将过去1小时内的风暴匹配在一起，图中用虚线表明了风暴的历史轨迹，虚线上的点为风暴在过去1小时内的实际位置。风暴预报算法中选择了TREC技术获取的运动矢量场(回波图中叠加了运动矢量)，实线表明风暴在未来1小时内的预报位置(间隔6分钟，未来1小时内总共有10个位置预报)，箭头则表明了风暴未来移动方向。

2.2 客观评分

在SWIFT中，还构建了风暴产品客观评分模块，可以实时运行。在FDP第二次测试期间，这个评分模块尚未投入业务运行。为了检验风暴产品，计算其误差，在2007年FDP测试结束后，对风暴产品进行了模拟实时客观评分，所使用的资料包括上面所有强对流个例。对于每一个风暴的10个预报时次(6，12，18，24，30，36，42，48，54，60分钟)都进行评分。

2.2.1 评分办法

在SWIFT系统中，对于同一个风暴(风暴ID是独一无二的)，在其生命史内，将其实况位置与预报位置进行比较，如：00时30分的实况位置与00时00分风暴产品的30分钟的预报位置相比，可以计算预报时效为30分钟的风暴产品的误差。

在客观评分系统中，分别计算X轴平均绝对距离误差、Y轴平均绝对距离误差、X轴平均距离误差和Y轴平均距离误差。处理时，先对每六分钟的风暴产品进行计算，然后对所有时次的风暴个例评分结果进行统计分析，以评估风暴产品的表现。绝对误差直接给出了不同预报时效风暴产品的可信度，而相对误差则在一定程度上表明了系统性的偏差。

2.2.2 参与评分的风暴样本数

在2007年FDP测试期间，总共出现了11次强对流过程，具体时间如上。SWIFT中的风暴产品识别出大量的风暴，在这些风暴中，既有孤立单体，也有带状、线状或成团成簇排列的多单体，因此能够较为全面的检验风暴产品。

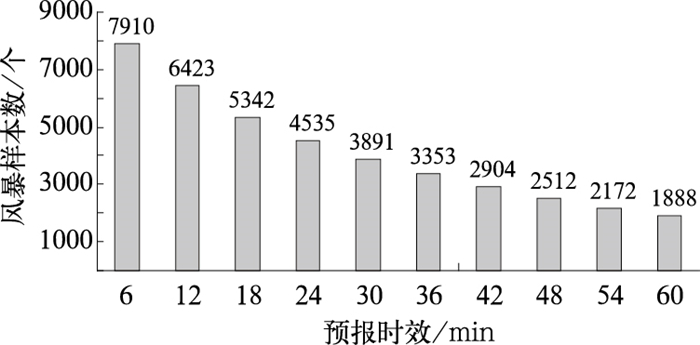
对于不同的预报时效，根据风暴生命史的不同，参与统计的样本数也不一样，图 2给出了不同预报时效参与评估的风暴样本数，随着预报时效的增加，参与评估的样本数是逐渐减少的，对于6分钟的预报时效，风暴数为7910，为最多；对于60分钟的预报时效，风暴样本数最少，为1888个。

2.2.3 评分结果统计分析

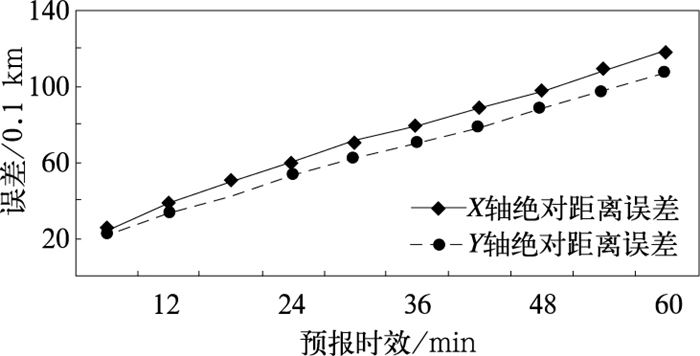
根据前面提供的风暴样本，统计了风暴产品在X轴和Y轴方向上的绝对距离误差，其中X轴对应为经向，Y轴为纬向，结果见图 3。分析表明，随着预报时效的增加，风暴产品在X轴和Y轴方向上的绝对误差也增加，X轴方向上的误差略大于Y轴(即经向上的误差要略大于纬向)，但两者的增加趋势相似。对于6分钟的预报时效，风暴产品的绝对误差最小，在X轴和Y轴上分别对应为2.5 km和2.2 km；至60分钟时，绝对误差分别达到了11.8 km和10.7 km；当外推超过30分钟后，如36分钟，X轴和Y轴绝对距离误差分别为8.0 km和7.0 km，此时直线距离上的误差(即X轴和Y轴之和)超过了10 km，产品可信度降低。

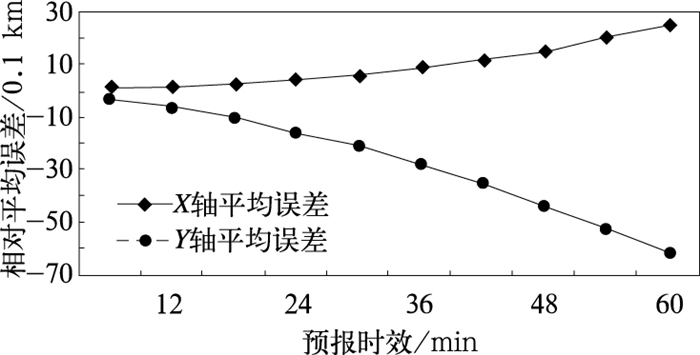
图 4还给出了风暴产品在X轴和Y轴方向上的平均距离误差。结果表明，在经向上，风暴预报时出现了系统性的偏慢(实际位置减去预报位置为正值)，即预报位置偏西；而在纬向上，预报出现了系统性的偏快，且偏差的幅度超过了经向。

3 小结

2007年，在“FDP”第二次测试期间，SWIFT系统中的风暴产品进行了应用。该风暴产品首先依赖于北京、天津和石家庄SA型雷达的拼图资料，在进行区域拼图之前，还对雷达基数据进行了超折射回波的抑制工作。

在识别风暴时，认为风暴具有三维结构，识别时利用多个阈值检验其强度和连续性；并采用了多阈值、核抽取、以及相近单体处理等多项技术，以解决成簇、成串排列的风暴或多个风暴相距较近时造成的误差。在对风暴追踪时，在距离相关的前提下，采用最大相似原则进行匹配；而对于风暴的位置预报，则采用了TREC技术获取的运动矢量场进行外推。

2007年7月和8月，北京地区出现了多次强对流过程，风暴产品可以与TREC运动矢量场、反射率因子域等叠加在一起，为预报员发布强对流天气临近预报和预警提供重要信息。对测试期间所有个例的客观分析表明：随着预报时效的增加，风暴产品的平均绝对误差增大，且在经向上的误差略大于纬向上；在预报时效为30分钟时，风暴产品在X轴和Y轴上的平均绝对误差为7.1 km和6.2 km，样本数为3891个；当预报超过30分钟后，直线距离绝对误差(X轴和Y轴之和)超过了10 km，该产品的可信度下降。另外，在经向上，风暴产品的预报出现了系统性的偏慢，而在纬向上，预报出现了系统性的偏快。