引言

基于高时空分辨率雷达资料的雷暴云团识别、追踪及预警技术是目前最重要的临近预报预警技术之一，主要方法有交叉相关(TREC)法和单体质心法等^[1-2]。交叉相关法^[3-4]把整个数据区域分成若干个小区域，相邻时刻雷达回波图像之间计算相关系数，通过最大相关系数确定相邻时刻图像中的区域，从而确定回波平均运动；该方法在国内得到广泛的应用^[5-9]；该方法缺点就是无法准确划分云团物理边界，得不到单体风暴的特征。单体质心法典型算法有WSR-88D和WDSS的风暴单体识别与跟踪算法SCIT^[10]和雷暴识别跟踪与临近预报TITAN^[11-14]，这两种方法都首先识别单体，然后在前后两个时刻的扫描数据进行单体匹配追踪，将风暴单体分离出来，然后通过多个时刻的追踪结果进行外推预警；SCIT方法只识别出个别的单体，不识别几个单体的复合体，也不给出单体的形态、体积和体积的变化；TITAN方法可以给出雷暴质心未来的位置之外，还增加了雷暴的形状、体积及变化，但还仅仅注重雷暴单体，须尽可能将相连的云团分离以提高预测的准确度^[15]，雷暴活动过程中的分裂、合并没有充分考虑，忽视雷暴群体的活动特征。

边界相关方法是一种利用模式识别技术进行云团边界识别、拓扑处理，建立生命周期与族谱关系，在自动识别雷暴云团的基础上对云团进行对象化处理，得出雷暴云团从发生以来的时间序列, 并进行外推预报。实例结果表明：该方法能够识别不同尺度对流云团，识别结果合理，根据预报时效的长短，选择不同的云团识别尺度，获得效果更为明显。

1 云团的对象化识别 1.1 云团边界识别

首先将雷达CAPPI数据优化为二值化图像数据，利用计算机图像识别技术对图像数据进行边界识别。

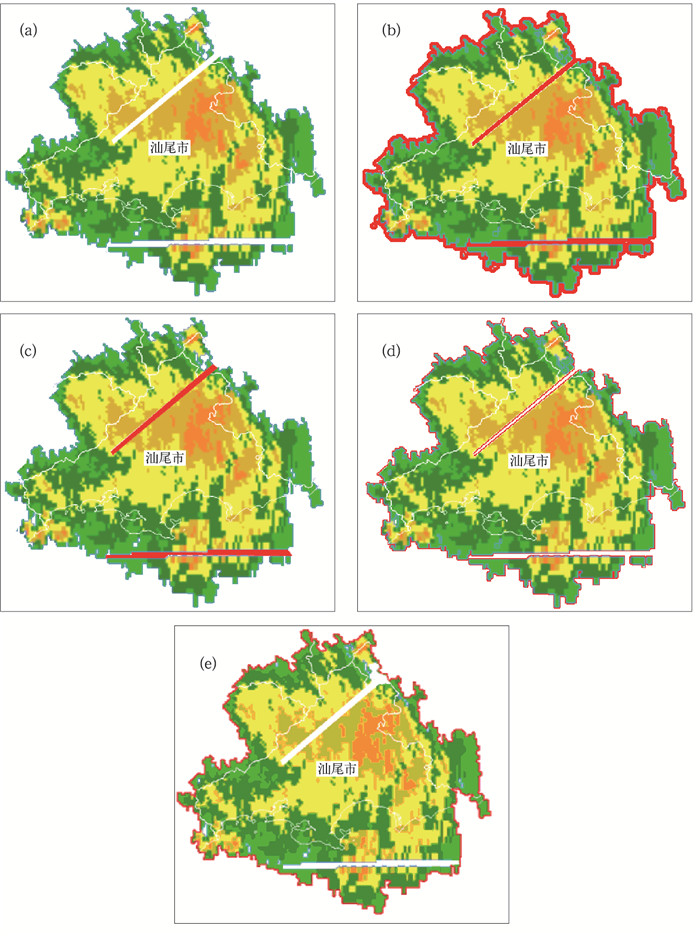
边界识别之前，最重要的一步是雷达缺线处理；雷达回波缺线经常给云团边界的识别和追踪带来严重困难。我们模型设计了“膨胀-侵蚀”的算法来解决这一难题。具体做法是：先执行回波的边界检测，然后边界向外膨胀1~2个格点，由于缺线一般是从雷达中心点出发宽度为数个格点的射线，如果边界向外膨胀2个格点，缺线扇面内就相应被填了4条线，因此缺线在4条线内的缺失扇面都被填塞了；但是真正的边界由此变宽，再次扫描边界，利用“侵蚀”算法还原外边界(如图 1)。“膨胀-侵蚀”具体算法是：(1)膨胀，二值图像空间内由上向下、由左向右进行逐行扫描，得到水平扫描线与云团边界的交点，交点像素P符合以下条件：P其值为“真”，但左边相邻像素值为“假”[称为左交点]或者右边相邻像素值为“假”[称为右交点]，左右相邻像素同时为“假”的情况不是交点；若是左交点，将交点左边二(或者一)相邻像素的取值设为“真”；若是右交点，将交点右边二(或者一)相邻像素的取值设为“真”；垂直方向也可以做类似操作。(2)侵蚀和膨胀算法相似，同样得到交点像素后，若是左交点，将交点右边二(或者一)相邻像素的取值设为“假”；若是右交点，将交点左边二(或者一)相邻像素的取值设为“假”；垂直方向也可以做类似操作。

下一步是进行边界识别：用图像边缘提取算法^[17]提取云团边界段，等待所有的遍历完成后，按照云团的几何特征将不封闭的边界段连接成若干封闭的边界, 这些封闭的边界经过拓扑关系来建立云团内边界和外边界。边缘检测是图像处理技术研究中的一个重要领域，也称为边缘提取，是利用图像像素的灰度或二值特征来获得图像的边界。

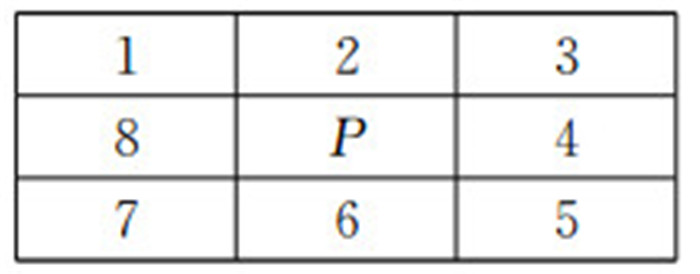
边界相关使用的边缘提取算法是一种特定的边界自动跟踪遍历形式：“N-近邻”跟踪遍历形式(N取值为8或者25)。N近邻有两种类型：1是直接近邻，即两个像素的相应单元共有一条边。2是非直接近邻，即两个像素相应单元仅在一个角上相接触；两种近邻在云团边界识别中均被使用；图 2是一个像素P与其他像素的“8-近邻”位置关系。

边界相关边缘提取算法首先在二值图像空间内由上向下、由左向右进行扫描得到第一个图像值为“真”的像素作为初始像素P1，利用“N-近邻”对初始像素的8个方向进行跟踪(总是选择最右边或者最左边的像素为所得的像素)，必在一个方向上找到下一边界像素点P2，再利用P2“N-近邻”关系，找到下一边界像素点P3，如此逐点跟踪，若当前像素与初始像素相同或者已经遍历过，跟踪算法结束, 得到一条边界段。

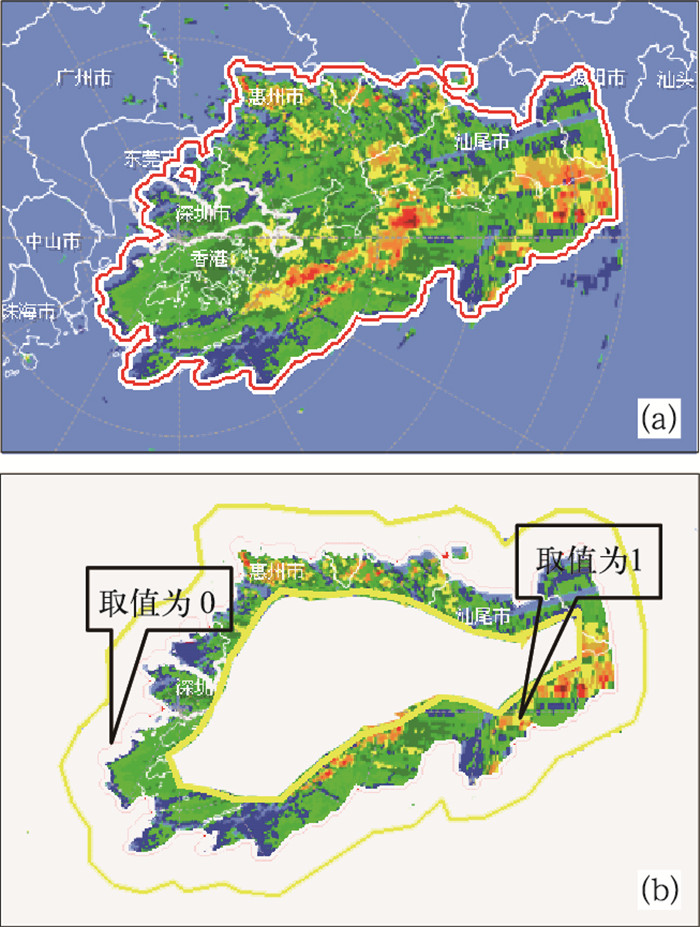
云团轮廓曲线得到后，利用轮廓曲线是否存在能量突变来判定是否为有效边界, 来排除识别错误，做法是以轮廓线为中心线，制作轮廓线的缓冲区，然后以此环形缓冲区与雷达回波做空间叠加分析(图 3)；对环形缓冲区内的回波进行二值化处理(有回波处取值为1，无回波处取值为-1)后对结果进行累加，累加值与环形缓冲区面积之比越趋向于零，说明轮廓线的质量越可靠。

1.2 云团拓扑关系建立

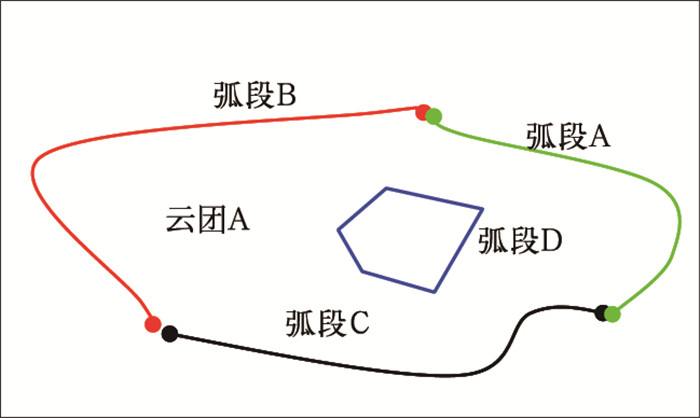
拓扑关系^[16]定义包括邻接性、连通性、方向性、包含性。其空间逻辑意义重于其几何意义。由于组成云团的轮廓线是由若干弧段[Arc Segment]构成，并且弧段依次首尾相连组成一个封闭的环。如图 4，云团A由弧段A、B、C、D构成，其中A、B、C构成外环，D构成内环，A、B、C有根据其邻接性、连通性、方向性构成外环，D通过与外环的包含性来确立为内环。

在云团的追踪过程中，仅靠边界提取法并不能完全识别出一个完整的云团，因此要根据云团由若干封闭环(分为内环和外环[rings])构成这一几何特征，建立边界间的连通关系，从而得到正确的雷暴云团。

在云团追踪过程中还需要用到另一种拓扑关系——包含性；由于云团内部可能存在若干孔洞，需要将若干有包含关系的边界组合为一个独立的云团。

获得云团集合后，需要根据云团的几何边界统计云团内部的平均强度，如式(1)：

$ {\overline Z _{xy}} = \frac{{\sum {_{i \in {N_{xy}}}{Z_i}} }}{{{N_{xy}}}} $

(1)

式中Z_i是云团几何边界内第i个雷达回波格点的强度，N_xy云团几何边界内雷达回波格点的集合。

2 云团生命时序的建立 2.1 云团对象化识别的判别因子

云团外推的前提是判断云团所处的生命时序和族谱关系，也就是在给定的时次序列中，建立某一云团对象以时间排序的序列，这些对象序列是以时次先后排序的云团链表；云团链表中任两相邻的对象是彼此相似的，不相邻的对象由于时间间隔较长，云团变化较大，不要求其相似；如图 5所示。关于云团的相似性确定，有一组判定因子，将在下面详细介绍。

云团的相似性判定，需要有很高的准确率，少量的误判或漏判将会严重影响追踪的质量。

经过反复试验，边界相关云团外推模型确定了一组相似性判定因子，它们相互主次分明，相互协同工作，较大提高了识别的准确性。

这一组因子分别是：四分树匹配分析因子、重叠因子、面积因子、外接矩形因子、轮廓综合因子、局部相似判定因子。其中四分树匹配分析因子是主因子，其他因子是用来纠正误判或漏判的，它们是根据两云团的几何与拓扑特征来确定相互间的协调关系。

(1) 四分树匹配度因子

对云团A和云团B用相同的矩形进行取景，然后根据取景矩形的大小将云团A和云团B分别在长度和宽度为2N×2N的网格空间中栅格化；通过检查网格空间中的网格值来判定相似度。当云团A和云团B网格值的重叠数据与总网格数的比值大于75%时，该因子认为两云团是相似的。

边界相关云团外推模型用四分树编码的方式逐步提高的栅格密度，同时降低相似度的阈值，来检验相似的可靠性。

四分树编码又称为四叉树、四元树编码。这种方法将2n×2n像元阵列的区域，逐步分解为包含单一类型的方形区域，最小的方形区域为一个栅格像元；其区域划分的原则是将区域分为大小相同的象限，而每一个象限又可根据一定规则判断是否继续等分为次一层的四个象限。其终止判据是，无论任何层次上的象限，只要划分到仅代表一种对象或符合既定要求的几种对象时，则不再继续划分，否则一直分到单个栅格像元为止。根据四分树这种特点来识别特定类型的云团是非常合适的。

另外，相似判定成功后，也可以用两云团的强度信息求出两云团的相关系数，来验证相似度的可靠性。如式(2)所示。

$ R = \frac{{\sum {{Z_1}\left( i \right){Z_2}\left( i \right)} - {n^{ - 1}}\sum {{Z_1}\left( i \right)\sum {{Z_2}\left( i \right)} } }}{{{{\left[{\left( {\sum {Z_1^2\left( i \right)-n\overline Z _1^2} } \right)\left( {\sum {Z_2^2\left( i \right)-n\overline Z _2^2} } \right)} \right]}^{\frac{1}{2}}}}} $

(2)

式中Z₁、Z₂是T时刻和T+Δt时刻云团的强度，n为云团包含的格点数；通过式(2)可以求出间隔Δt时间的两个云团的相关系数。如果相关系数低于阈值，则说明存在误判。

相关系数的取值应在0.20到0.90之间, 过小值和过大值都不作为判断依据。

(2) 重叠因子

判断对云团A和云团B在空间位置上是否重叠，如果重叠是包含关系或者是局部重叠。不同重叠方式，来选用不同矩形取景方式，来判定是合并或者是分裂的。重叠面积与云团面积比值不应低于0.25。

(3) 面积因子

计算云团A和云团B面积，计算小云团面积与大云团之比，如果比值大于0.75，则认为面积相似, 否则认为不相似; 如果面积不相似，进行局部相似检查。如果云团内部有孔洞，还要扣除孔洞的面积。

(4) 外接矩形因子

判断对云团A和云团B在外接矩形是否重叠。如果云团A和云团B在空间位置上不重叠，但它们的外接矩形重叠，也要进行更进一步的判断。外接矩形因子取值为“真”、“假”两种情况。

(5) 轮廓综合因子

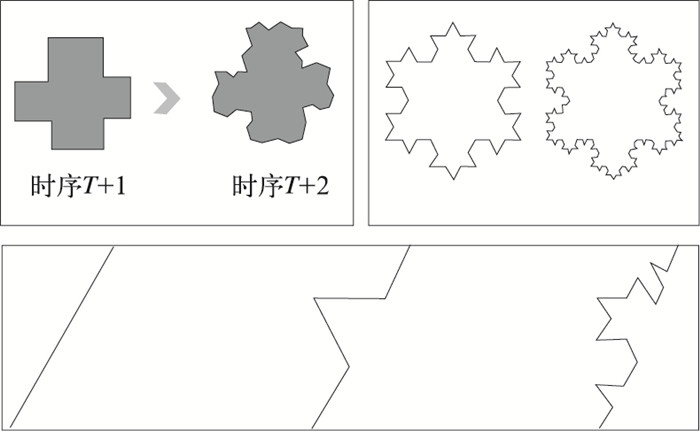
针对整体相似、局部不相似的云团，必须用轮廓综合因子来判定(图 6)。将云团A和云团B的轮廓进行综合，忽略局部细节，提高相似判断的准确度。轮廓综合是对云团边界矢量坐标的“抽稀”算法，根据指定的容差步长，将边界矢量多余坐标去掉，从而忽略局部细节。该因子的容差步长一般取值为2~8km。

(6) 局部相似判定因子

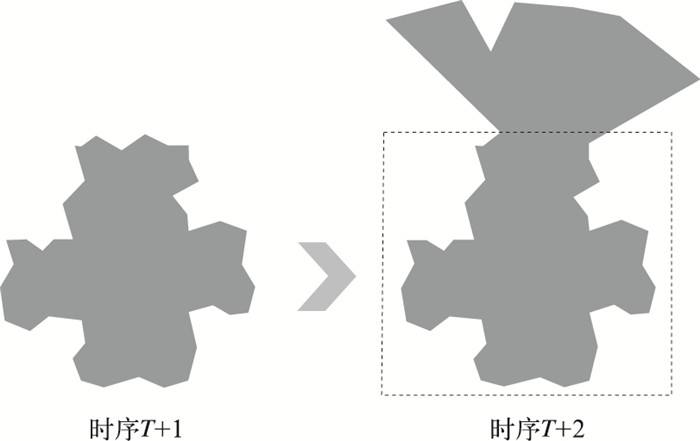
局部相似判定是以上几种方式的综合，用于确定云团的分裂或合并。具体做法是：以较小云团的外接矩形作为取景矩形，分别对两个云团取景，然后调用四分树匹配度分析因子，来判定云团的族谱关系。如图 7所示。

由于上述判断为矢量运算，或者将矢量转为栅格后进行叠加运算，再考虑到较长的时间尺度，建立识别并建立云团的族谱关系需要较大的运算量，速度问题会影响到系统的应用效果。为了解决这一问题，边界相关云团外推模型采取了寻找云团的等价矩形，来简化运算。同时等价矩形也是进行云团强度变化外推的重要手段，下文还将讨论。

云团等价矩形运用的原理是：由于矩形与矩形的空间运算是比较运算，因此速度很快，利用这个特点，在执行相似性判定因子判断前，先比较等价矩形是否相似，如果相似再做下一步运算；这样就可以节约大量运算时间。

另外等价矩也可以承载各方向异步的强度变化信息，做法是将等价矩形细分为网格，将经过反飘移处理的云团按照一样数目的行列也细分为网格，再以网格为单位综合出云团各部分的强度信息，并存储于等价矩形中，通过比较两个云团等价矩形，可以求出云团各方向的强度变速速率，为外推做准备。

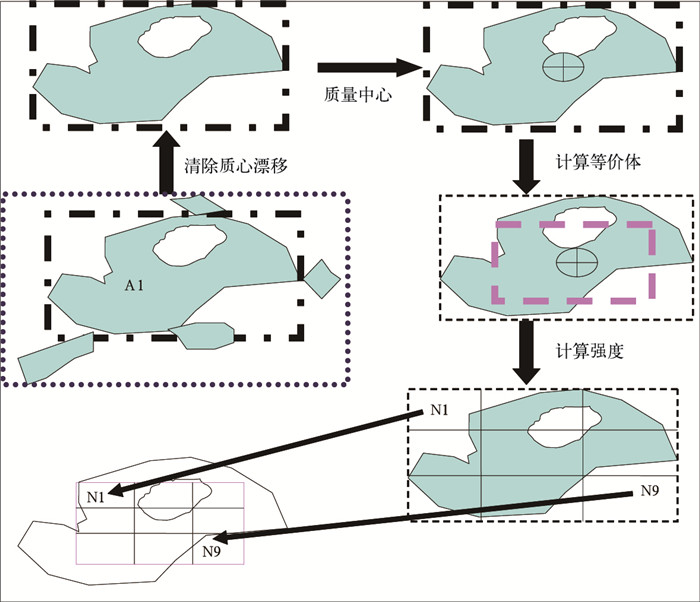
边界相关云团外推模型对等价矩形的定义是这样的：对云团A执行“侵蚀”运算，也就是细化运算，去除“悬挂”于云团A的碎片(如图 8示)得到云团A1，然后计算云团A1所包含的格点的平均坐标作为等价矩形的中心，云团A1所包含的格点作为等价矩形的面积，云团A1外接矩形框的长宽比作为等价矩形的长宽比，然后划分等价矩形为N×N个单元，用距离平方加权算法计算各个网格平均强度。

由此可以看到等价矩形的诸多优点：(1)能反映出云团扣除内部孔洞的真正面积；(2)能反映出云团真正位置和方位，不受漂移碎片的影响；(3)等价矩形内部网格可以准确表达云团个方位的强度变化；(4)两相近云团的等价矩形更容易统一坐标系和正则化，以便建立等价矩形内部网格的对应关系, 从而实现强度变化速率的求解。(5)执行速度快。

2.2 云团族谱关系

族谱关系是指同一云团在不同观测时次中的时间关系、分裂与合并关系。

族谱关系是通过相邻时次云团的相似性检查，识别出云团发生发展消亡的运动轨迹，从而预测云团的运动趋势。一个典型的独立云团生命周期从出生到消亡，没有发生过云团合并或分裂出来的情况(图略)；这种云团外推的准确率是比较高的。另外一种典型情况就是云团A和云团B在发展过程中合并为一个新云团C，同时云团A和云团B消亡；预测新云团C的运动趋势是根据云团A和云团B运动趋势综合出来的，随着云团C的不断发展，积累到一定时次时，新云团C的外推也较为准确(图略)。还有更复杂的云团生命周期(图略)，云团A在发展过程中分裂为云团B、云团C、云团D，云团A消亡; 云团B、云团C、云团D各自按自己的生命周期运动发展；在某一时次云团D与外部云团T合并为新云团，同时云团D、云团T消亡；这样的过程是经常发生的，边界相关云团外推方法可以建立起各云团的父子关系、夫妻关系、兄弟关系；这些关系对建立外推模型是重要的。

3 云团外推模型

边界相关云团外推模型是根据雷暴云团运动惯性对云团的移向、移速、强度变化进行线性外推，预测雷暴云团未来某时刻的边界和位置。但雷暴的移向和移速，仅依靠雷暴二维的质量中心来计算云团的移动方向和速度显然是会带来很多误差，订正的原则是某一云团与其相邻的云团的速度差不能超过5m·s^-1，与周围平均云团方向偏差超过25°。超过这阈值则以周围平均移向和移速取代。以下分别对移向、移速、强度变化的确定具体分析。

边界相关外推模型首先确定几个原则来评估运动方向的可靠程度：(1)不位于雷达探测边界上的独立雷暴云团，如果其强度变化幅度较小，则其运动方向最可靠。(2)对于经历若干合并与分裂过程或者其生命周期内在雷达探测边界上活动过的复杂雷暴云团，则其运动方向可信度最低，其处理办法在下文具体描述。(3)位于前两种情况之间的情况，采用参照物对比的办法来确定运动方向的可靠程度。模型以最可靠的雷暴云团为参照，进行若干具体指标对比，如果具体指标越接近参照物，可靠程度就越高；具体的比较指标有：雷暴云团上下两个时次的回波重叠率、强度变化振幅、面积变化振幅等。

其次，对于雷暴云团的运动速度，由于计算云团质心时会带来累计误差，云团运动速度往往比实际偏快，外推模型采取“宁慢勿快”的原则：(1)移动速度超过门限值的序列不参加运算；(2)偶尔缺图也是造成速度不稳定的因素，缺图的时次采用雷暴云团生命周期内速度最小的时次。(3)去除质心漂移后计算速度。(4)对于经历若干合并与分裂过程或者其生命周期内在雷达探测边界上活动过的复杂雷暴云团，速度变快的可能性较大，可采用雷暴云团生命周期内速度最小的时次。

第三，强度变化推算需要根据云团尺度的大小采用不同的处理方法，小尺度云团直接使用平均强度统计结果，大尺度云团由于跨度很大，各个部分回波强度变化不一致，比如一部分在增强，另外一部分在减弱，因此边界相关云团外推模型将大尺度云团按照等价矩形的方式划分为网格，按网格计算强度变化，依此来校正外推结果。

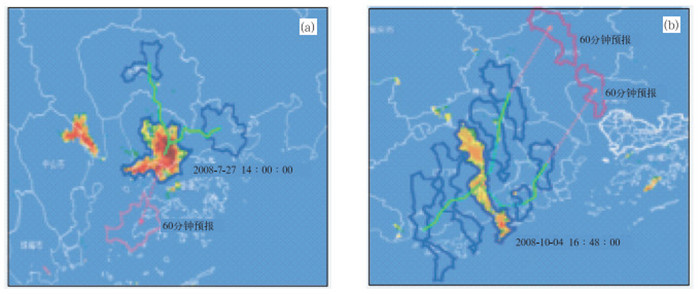
有两类云团移向、移速需要重新订正：(1)经过大的分裂与合并的云团，质心突变造成移动方向和速度的突变；也有些雷暴云团所有序列的计算结果都是无效的；(2)位于雷达探测边界上的云团，得到的云团信息是片面的。边界相关能有效识别以下几种情况：经过分裂与合并的序列、移速异常的序列、与大部分序列运动方向背道而驰的序列、处于或曾经处于雷达探测边界的序列情况；这些序列由周围序列的平均速度和方向取代。图 9(见彩页)为深圳雷达观测到的一个云团合并和分裂的观测实况和TRACER的外推预报显示图，可以看出，TRACER可以识别和追踪雷暴的合并和分裂过程，并作出预报。

4 边界相关识别技术的业务应用和个例检验

边界相关外推方法对云团进行对象化识别，有利于建立对象化的信息识别和外推预报。边界相关云团外推模型以云团为操作对象，云团与地理信息系统叠加显示，可以用鼠标选中云团，系统云团以属性的方式显示该云团的出现时间、中心强度、运动速度等，在GIS背景上可以立刻得到云团未来15分钟、半小时、1小时位置。

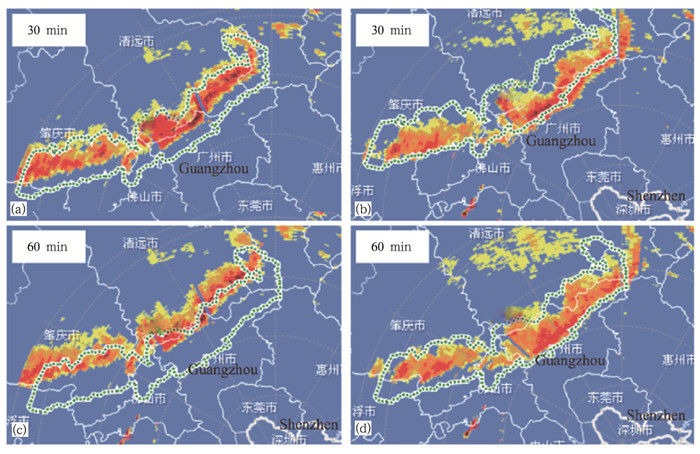
我们选取深圳雷达2007年4月23日的一次天气过程的两个时段进行云团的识别、跟踪及临近预报(图 10)。通过预报和验证实测图像的比较，60分钟以内的预报是可以接受的，预报边界和观测图像重叠度比较高。

在实际应用中，预报员通过追踪云团的发展轨迹，了解不同的云团的生命史和尺度差异，针对不同的云团选择不同的时间尺度和回波阈值进行识别和追踪，如对于小云团可以选择时间尺度比较短(30min以内)、回波阈值在15dBz以上进行识别和外推；对于大云团可以选择时间尺度比较长(如1h以上)、回波阈值在35dBz以上进行识别和外推，可以改进预报结果(图略)。在实际业务中，本算法既可以识别和跟踪强雷暴云团，对交叉相关不好跟踪的小云团的识别追踪也很有效。

5 结论和讨论

本文介绍了雷暴云团边界相关追踪技术以及基于该方法的一种雷暴云团的自动识别和追踪系统(简称“追踪者”，TRACER)的基本原理和方法。

TRACER有三个关键技术环节：(1)雷暴云团的识别处理技术：对雷达回波进行二值化运算，采用“膨胀-侵蚀”的算法有效地解决雷达回波缺线问题，综合应用四分树匹配分析因子、重叠因子、面积因子、外接矩形因子、轮廓综合因子、局部相似判定因子等六个判断因子，高效地识别出每个云团的时间序列和族谱关系，对云团进行对象化识别和处理。(2)算法优化技术：应用云团的等价矩形，可加快识别和追踪速度，消除云团的质心漂移，保留云团各方向的强度变化信息；提高每个云团的运动方向、速度、面积、强中心，以及所处的状态(增强或减弱、膨胀或缩小)等信息的准确性。(3)雷暴云团外推预报：在获得雷暴云团的生命周期和族谱后，边界相关追踪技术根据雷暴云团运动惯性对云团的移向、移速、强度变化进行线性外推。速度外推采取“宁慢勿快”的原则，面积变化主要根据云团面积膨胀系数对线性外推预报结果进行修正；强度变化推算需要根据云团尺度的大小采用不同的处理方法，小尺度云团直接使用平均强度统计结果，大尺度云团按照等价矩形的方式划分为网格，按网格计算强度变化，依此来校正外推结果。

TRACER方法与TITAN和SCIT方法比较：(1)TITAN识别雷暴的三维结构，然后将三维结构投影为二维结构，最后以椭圆或多边形来拟合雷暴投影的二维结构。TRACER虽然只识别雷暴的二维平面结构(CAPPI)，但是按雷暴云团的实际形状来识别和追踪，没有用椭圆或多边形来拟合；SCIT仅提供雷暴的质心，不给雷暴的形状。(2)TITAN和SCIT重点是识别和追踪雷暴单体，对于复合体等复杂雷暴简化为单体来处理，TRACER则既可识别单体，也可识别复杂体。(3)TRACER和TITAN不仅提供雷暴云团中心的历史移动轨迹, 还提供每个雷暴云团形态、强度变化特征，可以记录每个强雷暴云团影响的区域；但TRACER按对象化来识别和追踪雷暴云团，还可识别雷暴云团的合并和分裂，SCIT仅提供雷暴历史移动轨迹。

初步实例分析表明该方法具有较好的临近预警预报能力，该方法已经作为实时业务系统重要方法应用于深圳市气象局的临近预报预警业务中。本算法是雷暴云团的对象化识别和跟踪的一种有效算法，实例表明对雷暴云团的外推需要根据雷暴云团的范围、强度和生命史长短，采取不同的时间尺度和dBz阈值进行识别和外推，可有效提高外推预报准确率。鉴于雷暴发生发展和演变机理的复杂性，本方法还需要在业务实践中不断分析、评估和改进。