2. 吉林省气候中心;
3. 江苏省气象局
2. Jilin Climate Center;
3. Jiangsu Meteorological Bureau
近年来,能源危机成为人类共同面对的世界性难题,风能作为一种清洁、可再生、储量很大的能源受到广泛关注。为了满足开发需求, 了解风能分布,中国先后进行了多次风能资源普查,但都是基于10m高度的气象站资料[1-2]。目前,风机轮毂高度多数在60~70m,随着风电技术的发展,还有可能提高,因此需要用现有资料评估风机高度上的风能资源。
近地层风速随高度变化规律的研究已经比较成熟。一般认为,风速随高度服从指数或对数分布,对数律主要适用于中性条件下的近地层,指数律则可推广至非中性大气,全边界层可广泛适用[3];丁国安等[4]对低层瞬时风速的廓线类型进行了统计,发现符合指数律的只占样本的一半,但长时段平均风速符合指数律;大量研究认为,指数律更符合平均风速随高度的变化[5-9]。
许多学者在风功率密度廓线方面都有研究。朱超群[10]用指数律描述风功率密度的高度变化,并给出指数与参考高度上风功率密度及其他风速统计量的经验式;屠其璞等[11]则通过计算不同高度上的Weibull参数,推算平均风功率密度。
由于风功率密度受下垫面性质和大气稳定度影响显著,同时风功率密度为风速的三阶矩,统计抽样误差较大,目前,风功率密度廓线的观测资料和理论分析尚不很完善。本文利用江苏和吉林的测风塔资料,分析风速和风功率密度廓线特征,并尝试将平均风速和Weibull分布率相结合,用于推算不同高度的风功率密度。
1 资料说明江苏的测风塔位于其东北部沿海,吉林的位于其西北部平原,资料为每10分钟风速、风向资料,按照规范取整点前10分钟平均风速作为小时平均代表值,所用资料时间长度均在一年左右。
|
|
表 1 测风塔资料概况 |
由于测风塔没有气压、水汽压、温度观测资料,因此用临近台站历史资料计算10m高度空气密度,再进行高度推算。事实上,空气密度是一个较稳定的量,同一地区同一高度量级差别仅为10-2~10-3,不同高度差别也很小。
2 平均风速、风功率密度廓线特征分析平均风功率密度是单位时间内气流通过与气流垂直的单位面积的风能,实测逐时资料适合用直接统计法计算[12]:
| $ \overline W = \frac{1}{{2N}}\sum\limits_{k = 1}^{12} {\sum\limits_{i = 1}^{{n_k}} {{\rho _k}V_{k, i}^3} } $ | (1) |
式中,W为年平均风功率密度,N表示该时段内风速观测时数,ρk为第k个月月平均空气密度,nk第k个月的观测小时数;Vk, i第k个月的风速序列。
平均风功率密度随高度呈指数增加(图 1),这与平均风速廓线特征相似。一般认为平均风速和平均风功率密度满足下面两式:
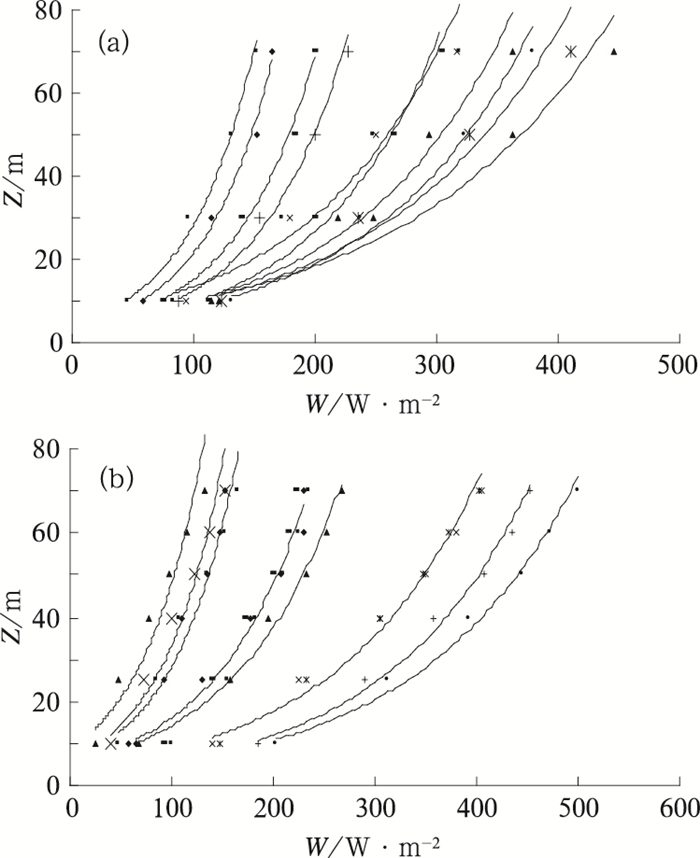
|
图 1 各月平均风功率密度及指数拟合曲线 (a)江苏竹港70m塔;(b)吉林双辽70m塔 |
| $ {\bar V_n} = {\overline V _1}{(\frac{{{Z_n}}}{{{Z_1}}})^\alpha } $ | (2) |
| $ {\bar W_n} = {\overline W _1}{(\frac{{{Z_n}}}{{{Z_1}}})^N} $ | (3) |
其中,Vn,Wn和V1,W1分别为高度Zn和Z1处的平均风速、平均风功率密度,α,N为平均风速、风功率密度随高度变化的指数(下文简称风速、风能廓线指数),与大气稳定层结和下垫面性质有关。
|
|
表 2 年平均风速、风能廓线指数 |
本文统计了各塔年平均风速、风功率密度廓线指数。风速指数分布在0.14~0.24之间,总体而言,吉林略大于江苏,这反映了我国北方地区比南方大气稳定的基本特征;风功率密度指数变化幅度较大,但均小于3倍的平均风速指数,与不少文献指出的3倍关系相差较大,这是由于平均风功率密度是风速的三次方函数,不仅取决于平均风速,还与风速概率分布的偏态特征相关。
下垫面粗糙度和近地层大气稳定度是影响风能廓线指数的主要因素,统计特征表现为平均风速和风速频率分布的差异。风速直接影响上下层大气间的垂直交换,风速愈大,交换愈强,水平风速的垂直切变愈小,使得风速廓线指数和风功率密度廓线指数都减小。由于下垫面对风速的影响随高度逐渐减小,风速概率的偏态发生改变,偏态系数CS[13]计算结果表明,所有测层上CS都大于零,即正离差占优势,随高度增加CS减小,因此平均风功率密度与平均风速的相对比值低层偏大,高层偏小,从而风能廓线指数小于3倍的风速廓线指数。
3 不同高度风能参数的推算方法 3.1 平均风功率密度的推算指数律可以较好地描述风功率密度随高度的变化,但由于风功率密度在统计上为三阶矩,抽样误差较大,不利于在无塔层观测地区进行高度推算。考虑到风速廓线的指数律已被广泛论证和认可,并且平均风速(一阶矩)的统计抽样误差较小,本文借鉴风功率密度与平均风速的关系,探讨一种新的风功率密度高度推算方案。
研究表明,风速概率分布与二参数Weibull分布较为吻合[14],风速概率密度函数可表示为:
| $ f(\mathit{V}) = \frac{K}{C}{(\frac{V}{C})^{K- 1}}\exp \left[{-{{(\frac{V}{C})}^{_{_K}}}} \right] $ | (4) |
其中,C为尺度参数,K为形状参数,与式(4)对应的风速分布函数为:
| $ F(V) = \int {_0^Vf(\mathit{V}){\rm{d}}\mathit{V = }{\rm{1}}} - \exp \left[ { - {{(\frac{V}{C})}^K}} \right] $ | (5) |
风速V的数学期望为:
| $ E(\mathit{V}) = C\Gamma (1 + \frac{1}{K}) $ | (6) |
Γ为伽马函数。因此,平均风功率密度和平均风速对应的风功率密度可表示为:
| $ E(\mathit{W}) = \frac{1}{2}\rho E({\mathit{V}^3}) = \frac{1}{2}\rho {C^3}\Gamma (1 + \frac{3}{K}) $ | (7) |
| $ E(\mathit{W'}) = \frac{1}{2}\rho {\left[{E(\mathit{V})} \right]^3} = \frac{1}{2}\rho {C^3}{\Gamma ^3}(1 + \frac{1}{K}) $ | (8) |
令
| $ \mathit{f = }\frac{{E(\mathit{W})}}{{E(\mathit{W'})}} = \frac{{\frac{1}{2}\rho {C^3}\Gamma (\frac{3}{K} + 1)}}{{\frac{1}{2}\rho {C^3}{\Gamma ^3}(\frac{1}{K} + 1)}} = \frac{{\Gamma (\frac{3}{K} + 1)}}{{{\Gamma ^3}(\frac{1}{K} + 1)}} $ | (9) |
可见,f仅与形状参数K有关,K体现了风速的频次分布特征,理论上取决于不同天气系统的活动频次和地表粗糙度。
由式(9)可得:
| $ E(\mathit{W}) = \frac{1}{2}f\rho {\left[{E(\mathit{V})} \right]^3} $ | (10) |
根据式(10),如果某一高度形状参数K及平均风速已知,便可推算该高度的风功率密度。不同高度的风速可以采用已经成熟的垂直廓线方法推算,形状参数随高度变化规律研究也较多,因此利用10m高度风资料可推算任意高度的平均风功率密度。
3.2 平均风速的高度推算目前,利用指数率进行平均风速高度推算的研究较多,但指数值受下垫面性质和大气稳定度影响难以确定。考虑到下垫面性质和大气稳定度与风速大小密切联系,本文提出一种以风速的概率分布为权重,风速分级加权平均的方法拟合不同高度的平均风速。
以10m高度逐时风速为标准,拟合了各级风速的廓线指数。随着风速从零开始增加,风速廓线指数迅速减小,达到6m·s-1后,变化趋于平稳。吉林6塔变化一致,江苏由于资料纬度和时间差异,分为两组,川东和竹港三塔风速指数变化近似,其余3塔比较接近。不难理解,在同一地区,同一时间段稳定度相似,若粗糙度相差不大,风速廓线指数主要取决于风速大小。
利用这个规律,本文以风速的概率分布为权重,用风速分级加权平均的方法拟合不同高度的平均风速。
| $ {\overline V _n} = \sum\limits_{i = 1}^n {{p_i}{{\overline V }_{10,i}}{{(\frac{{{Z_n}}}{{{Z_1}}})}^{{a_i}}}} $ | (11) |
V10, i为10m高度各级别的平均风速,pi为对应级别风速出现的频率,αi为该级别风速的廓线指数(表 3)。
|
|
表 3 各级别风速的廓线指数αi |
利用该方法拟合各高度的平均风速, 平均误差1.4%,最大误差6.2%,效果较好。需要指出, 该方法建立的前提是:稳定度相似、粗糙度相差不大,在不同地区,甚至不同年份,风速廓线指数可能存在较大的差异,在不同地区应用时须做适当调整,本文给出指数仅供东北平原及江苏沿海地区参考使用。
3.3 形状参数的高度推算估算形状参数K最常用的方法有两种:最小二乘法和风速变差法[15],本文计算认为后种精度更高,即:
| $ K = {(\frac{\sigma }{\mu })^{ - 1.086}} $ | (12) |
以平均风速V估计μ,以标准差Sv估计σ。
K在70m以下随高度升高而增加(图 2),Justus[16-17]的研究认为,K在60~70m左右达到最大值,然后随高度增加而减小,K/Kmax随高度变化曲线随季节和地理位置的变化甚小,Justus同时给出了K随高度变化的经验公式:
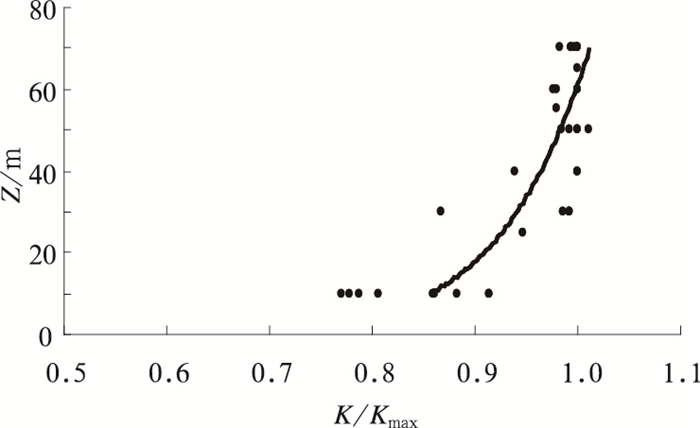
|
图 2 各塔K/Kmax随高度的变化 |
| $ K = {K_0}\frac{{1-0.088\ln ({\mathit{Z}_0}/10)}}{{1-0.088\ln (\mathit{Z}/10)}} $ | (13) |
K0为Z0高度的形状参数,式(12)的计算结果,也符合该式。
综上可知,根据Z1高度的逐时风速,可由式(11)、(13)、(9)得任一高度上的Vn, Kn和fn,再由式(10)可求得平均风功率密度。
4 拟合效果检验本文分别用上述方法和指数法推算不同高度的风功率密度,为了讨论两种方法在无塔层资料地区的应用性,所有指数采用交互验证法获得,即去掉某塔资料,由同组其他观测铁塔平均指数模拟推断该塔风功率密度,并进行误差分析,结果见表 4。
|
|
表 4 风功率密度高度推算及其误差分析 |
表 4中,Z为测层高度,W为实际风功率密度,W′e为指数法拟合值,即由式(3)推算,W′f为形状参数及平均风速法拟合值,Re,Rf为两种方法的拟合误差。
利用指数律拟合其他高度的平均风功率密度,平均拟合误差7.8%,最大误差22.9%;而根据形状参数和平均风速随高度变化规律拟合,平均误差4.4%,最大误差13.3%,远小于指数律,拟合效果较为理想。
5 结论利用测风塔资料,对江苏和吉林两个地区的风能参数进行了统计和分析,并探讨了一种利用10m高度风速资料推算近地层内任意高度上平均风功率密度的新方法。分析结果表明:
(1) 该地区平均风速和平均风功率密度的近地层高度廓线均与指数律相吻合。
(2) 无风速梯度观测站点的平均风速廓线指数,可由地面风速的频率分布推断。用该方法拟合不同高度平均风速的平均相对误差为1.4%,最大相对误差6.2%。
(3) 设风速服从Weibull分布,资料分析表明,其形状参数随高度变化满足式(13),因此可由10m风速资料推算各高度的形状参数。
(4) 平均风功率密度可表示为平均风速和形状参数的函数,因此,利用平均风速和形状参数随高度的变化规律,可由10m风速资料推算不同高度的平均风功率密度。应用该方法对现有铁塔资料进行交互拟合分析,其平均相对误差4.4%,最大相对误差13.3%,优于使用指数律推断的平均相对误差7.8%,最大相对误差22.0%的效果。
(5) 尽管平均风速的分级推算方法存在一定的地区局限性,但随着测风塔资料的增多、风廓线雷达的普及,可以采用更成熟的风速垂直廓线推算方法代替,缺陷将得到很大的弥补,因此,本文探讨的风功率密度高度推算方案具有一定的应用价值。
朱瑞兆, 1984. 我国太阳能风能资源评价[J]. 气象, 10(10): 19-23. DOI:10.7519/j.issn.1000-0526.1984.10.005 |
谭冠日, 1981. 关于风能资源分析的几个问题[J]. 气象, 7(11): 15-26. DOI:10.7519/j.issn.1000-0526.1981.11.008 |
徐大海, 1984. 大气边界层内风的若干特性及其应用[J]. 空气动力学学报, 2(3): 75-86. |
丁国安, 朱瑞兆, 1982. 关于低层大气风速廓线的讨论[J]. 气象, 8(08): 18-20. |
王志春, 宋丽莉, 何秋生, 2007. 风速随高度变化的曲线拟合[J]. 广东气象, 29(1): 1-15. |
傅抱璞, 于静明, 1981. 南京164米铁塔观测风速廓线的研究[J]. 南京大学学报(自然科学版), 17(4): 552-561. |
植石群, 钱光明, 2001. 广东省沿海风能的分析及计算[J]. 气象, 27(5): 43-46. DOI:10.7519/j.issn.1000-0526.2001.05.010 |
朱瑞兆, 薛桁, 1981. 风能的计算和我国风能的分布[J]. 气象, 7(08): 26-28. |
刘学军, 吴丹朱, 1991. 城市建筑群对低层大气风速廓线影响的统计分析[J]. 气象, 17(07): 14-18. |
朱超群, 1993. 风能计算及其随高度的变化[J]. 太阳能学报, 14(1): 7-15. |
屠其璞, 史慧敏, 1982. 我国风能资源的初步研究[J]. 南京气象学院学报, (2): 207-216. |
国家发展与改革委员会, 2004. 风能评估技术规范[M]. 北京, 1-18.
|
屠其璞, 王俊德, 丁裕国, 等, 1984. 气象应用概率统计学[M]. 北京: 气象出版社, 85-89.
|
么枕生, 丁裕国, 1990. 气候统计[M]. 北京: 气象出版社, 266-298.
|
张秀芝, 1996. Weibull分布参数估计方法及其应用[J]. 气象学报, 56(1): 108-116. DOI:10.11676/qxxb1996.011 |
Justus C G, 1976. Nationwide assessment of potential output from Wind powered generators[J]. Meteor, 15(7): 673-678. |
Justus C G, 1978. Methods for estimating wind speed frequency distribution[J]. Meteor, 17(3): 350-353. |
 2009, Vol. 35
2009, Vol. 35