新疆地处亚欧大陆腹地的中纬地区,远离海洋且被群山环绕,是著名的干旱、半干旱地区,新疆夏季(6—8月)降水有独特的时空分布特征[1]。新疆北部汛期暴雨洪水和持续性干旱等气候灾害异常活跃,对当地经济社会发展尤其是对农业产生影响很大。很多研究揭示了夏季我国区域降水异常与北半球甚至全球大气环流异常之间的联系[2-8],与热带太平洋、北大西洋以及北极地区的海气作用也有密切联系[9-11]。王健[12]分析了新疆夏季降水异常的同期500hPa高度场特征;王娇等[13]合成分析了北疆夏季多雨期与少雨期的500hPa高度距平场,发现它们呈现出趋势基本相反的分布形;杨莲梅等[14]研究了新疆夏季干、湿年代际背景下降水异常多、少年的500hPa高度场的差异,指出了其可能的物理机制;张友姝等[15]研究指出新疆夏季降水异常与同期以及前期冬季、春季的北半球极涡、中高纬度阻高等环流系统关系密切;魏香等[16-17]研究得到了新疆北部4—7月降水与前一年7月份开始的逐月NINO3区平均SST定量关系,谭艳梅[18]分析了北疆夏季降水与前期1月SOI的定量关系。
夏季(6—8月)降水是短期气候预测业务的主要内容之一,在新疆的短期气候预测常规业务中,每年1月发布的年景预测、4月初进行的全国汛期预测会商,5、6、7月初开展汛期滚动预测,都需要作夏季(6—8月)降水预测或给出滚动订正预测结果。在5月份作汛期滚动预测时,由于起报时间更接近夏季,相对而言前期环流因子物理意义更加明确。在考虑预测因子的不稳定性基础上,设计了滑动相关—逐步回归—集合分析相结合的方案,编写程序进行调试,建立物理统计模型,尝试提高和改进区域夏季降水预测业务水平。
1 资料和方法 1.1 资料选用新疆北部地区具有连续记录的29个气象站1961—2007年夏季(6—8月)降水量资料,计算了北疆区域1961—2007年逐年夏季降水指数。使用国家气候中心整理发布的1960—20 07年74类大气环流月指数。
1.2 资料预处理 1.2.1 降水指数计算根据陈兴芳等[2]提出的计算方法,应用公式(1)构建了北疆夏季(6—8月)降水指数序列。
| $ {{R}_{c}}=\frac{1}{n}\sum\limits_{i=1}^{m}{{}}\frac{{{R}_{i}}}{{\bar{R}}}+\frac{{{n}_{0}}}{n} $ | (1) |
式中,Rc为某年夏季降水指数,Ri为某站当年夏季(6—8月)的实测降水量,
|
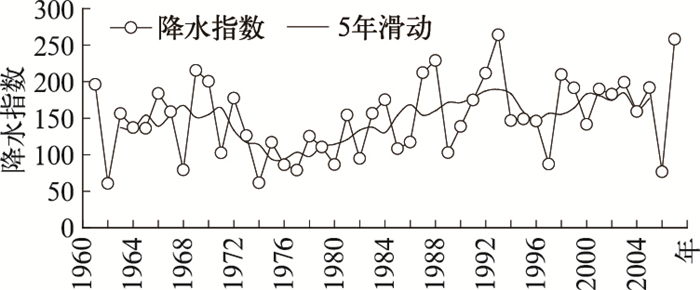
图 1 北疆区域夏季(6—8月)降水指数 |
为了诊断前期环流因子持续异常的影响,用前一年5月至当年4月的环流指数,计算了持续时间分别为1个月、2个月、3个月、4个月、5个月、6个月的57个组合,共得到备选环流指数因子数4218(74×57)个。
1.3 分析方法(1) 对降水指数序列进行蒙特卡罗线性趋势的显著性检验[19],在0.05显著性水平下北疆夏季降水指数序列n年来呈显著增加的线性趋势,滤去降水指数序列的线性趋势。对所有前期环流因子序列进行同样的线性趋势的显著性检验,同样滤去在0.05显著性水平下有显著趋势的环流因子的线性趋势分量,无显著线性趋势的因子则计算得到距平序列。
(2) 用滑动相关分析法选取建立初选因子库。分别对各滑动窗口的相关系数序列进行统计,第一,计算平均值,第二,计算均方差。满足下列条件之一的因子方可进入初选因子库:该因子与预测量之间的滑动相关系数平均值的绝对值超过了预测量在0.10显著性水平下的临界相关系数,而且滑动相关系数中的最后1个的绝对值不小于前一个,而倒数第2个相关系数超过预测量在0.10显著性水平下的相关系数临界值,同时,滑动相关系数的均方差不超过某临界值。随滑动窗口长度从小到大,均方差的临界值按等差数列从0.05到0.005降序排列。各滑动窗口长度下的不同显著性水平所对应的临界相关系数用蒙特卡罗检验法[19]确定。
总样本数为n时,滑动窗口长度sn分别取15,16,17,…,n-1,对应有n-15个初选因子库。
(3) 建立初级回归模型。用逐步回归方法,以滤去显著线性趋势的降水指数序列为因变量,以各初选因子库中的滤去显著线性趋势或者距平处理后的环流指数为回归因子,建模样本数取n,入选和剔除因子的F检验值分别为:F1=5.51、F2=5.50。得到n-15个初级回归序列。
(4) 建立一级集合模型。用逐步回归法,再次以滤去显著线性趋势的降水指数序列为因变量,将n-15个初级回归模型的拟合序列作为回归因子。建模样本数mn1分别取30,31,32,…,n-1,n,可以得到n-30+1个一级集合序列。
(5) 建立二级集合模型。用逐步回归法,以降水指数原始序列为因变量,以n -30+1个一级集合结果叠加上北疆降水指数线性趋势的序列为回归因子,建模样本数mn2取n,得到1个二级集合序列。
(6) 逐级反推寻找有显著统计关系的前期环流指数因子。从二级集合模型向初始环流指数因子库反推,逐级寻找入选模型的因子。即,入选二级集合模型的因子序列(一级集合模型结果)——入选一级集合模型因子序列(初级回归模型结果)——入选初级回归模型的因子序列(前期环流指数)。从统计学角度上讲,被挑选出的环流指数因子与北疆夏季降水指数序列之间有显著的统计关系。
(7) 确定降水指数异常高(低)年对应的前期环流指数指标。从北疆夏季降水指数序列中挑选出异常高9年和异常低9年,分别计算异常高、低年份对应的前期环流指数因子平均值,用统计t检验方法,对异常高9年与47年、异常低9年与47年以及异常高9年、异常低9年所对应的各环流指数之间均值的差异进行显著性检验,进一步识别有显著统计关系的前期环流因子对北疆夏季降水指数异常偏高、偏低年的预测能力。
(8)总样本数分别取n-1,n-2,n-3,…,n-10,重复步骤(1)~(6)。对得到的11个预测模型结果进行集合分析,用算术平均值方法给出每一个预测年份的统计集合预测值,并进行趋势预测准确率和均方根误差检验分析。
2 分析结果以样本总数n=47为例,对第n+1年(即2008年)的预测分析结果如下。
2.1 初级回归结果初级回归模型记为
|
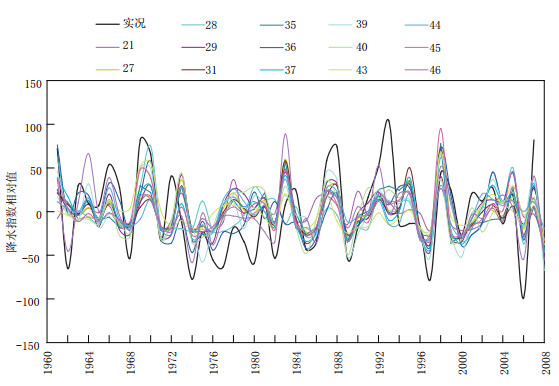
图 2 降水指数序列的初级回归结果 |
一级集合模型记为
|
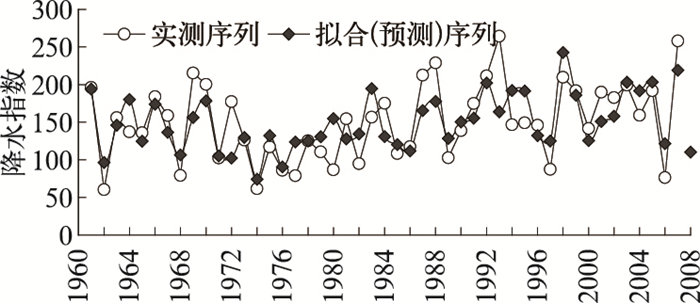
图 3 指数的集合回归结果 |
北疆夏季降水指数序列的二级集合模型的入选成员为建模样本数为47时的一级集合结果序列,而该一级集合模型中入选了2个成员,分别是滑动窗口长度sn为36、46的初级回归结果序列。滑动窗口长度sn为36、46的初级模型中,各有2个入选的前期环流指数因子(表 1)。
|
|
表 1 与北疆降水指数有显著统计关系的前期环流指数因子 |
入选一级集合模型的初级回归模型有2个,分别是滑动窗口长度为36、46的初级模型,X 1,X2,X3,X4分别对应表 1中的前期环流因子,则滤去线性趋势或计算距平之后的2个方程如下:
| $ $$\eqalign{ & \hat Y_{36}^0 = 5.574{X_1} + 0.638{X_2} \cr & R = 0.6673\;\;\;\;\;\;F = 17.66 \cr} $$ $ | (2) |
| $ $$\eqalign{ & \hat Y_{46}^0 = 7.318{X_3} + 2.122{X_4} \cr & R = 0.6638\;\;\;\;\;\;F = 17.33 \cr} $$ $ | (3) |
入选二级回归模型的一级回归结果序列有1个,是建模样本数n=47的模型,方程为:
| $ $$\eqalign{ & \hat Y_{47}^1 = 0.6235\hat Y_{36}^0 + 0.6105\hat Y_{46}^0 \cr & R = 0.6913\;\;\;\;\;\;F = 20.14 \cr} $$ $ | (4) |
Y′为北疆夏季降水指数1961—2007年的线性趋势序列,见式(5),其与自然数序列的相关系数R=0.4028,超过了0.05显著性水平下蒙特卡罗检验临界值(
| $ {{Y}^{'}}=129.9t+123.17 $ | (5) |
最终结果序列
| $ \begin{align} & \ \ \ \ \ \hat{Y}_{\text{47}}^{\text{2}}=\hat{Y}_{\text{47}}^{\text{1}}+{{Y}^{'}} \\ & R=\text{0}\text{.7248}\ \ \ \ \ F=\text{49}\text{.81} \\ \end{align} $ | (6) |
以上式(2)、(3)、(4)、(6)中,建模样本数n=47,入选因子数p为1或2,回归方程遵从分子自由度为p,分母自由度为n-p-1的F分布,F检验值用式(7)计算:
| $ F = \frac{{\frac{{{R^2}}}{p}}}{{\frac{{1-{R^2}}}{{n-p-1}}}} $ | (7) |
式(7)中R为回归方程的复相关系数,p为入选模型的因子数,n为建模样本数。
以上4个回归方程的F值远远超过了0.01信度水平下的临界值(注:
根据47年降水指数序列升序(降序)排列的前9位确定异常低(高)年(表 2)。升序排列时1982年列第9位,指数值为94.7,降序时2003年列第9位,指数值为199.3。挑选出的异常年份与正常值150的偏差量几乎都在50以上。
|
|
表 2 北疆夏季降水异常偏多、偏少年 |
用“1.3”节步骤(7)进行检验,结果见表 3。在0.10显著性水平下,4个因子对应的异常偏低9年与47年的平均值之间均存在显著差异,3个因子对应的异常偏高9年与47年的平均值之间存在显著差异。分别以降水指数异常偏高(低)9年对应的各因子的平均值作为定性预测北疆夏季降水异常偏多(少)的临界值(表 4)。
|
|
表 3 北疆夏季降水指数异常高(低)年前期的环流指数值差异检验 |
|
|
表 4 北疆夏季降水指数异常高、低年对应的前期的环流指数指标 |
以上分析是在样本数n=47时的结果。为了进一步检验该方法的预测能力,总样本数n 分别取46, 45, 44, 43, 42, 41, 40, 39, 38, 37时,重复分析步骤(1)~(6),又独立建立了1 0个集合预测模型。11个模型都可以得到从第n+1年到2008年的预测值(表 5)。
|
|
表 5 各模型的预测结果 |
当总样本数n分别取37, 38, 39, …, 47时,得到了11个预测模型,选取每一个模型的第n+1年的预测值,组成1998—2008年的预测序列(表 6)。
|
|
表 6 预测检验参数 |
11个预测序列结果中,有11个模型可以给出2008年预测值,以此类推,2007年对应有10个预测值,……,1998年对应有1个预测值。计算1998—2008年逐年所有预测值的算术平均值和均方差。用算术平均值方法,得到统计集合预测序列(表 6)。
2.7 独立样本检验分析趋势预测准确率与均方根误差。趋势预测指对北疆区域夏季降水偏多或偏少的趋势预测,趋势预测准确率通过以下计算得到:预测值以及对应的实测值均减去150后符号相同的年份占检验年份的比率。
(1) “第n+1年”预测序列检验。选1998—2007年独立样本,“第n+1年”预测序列的趋势预测准确率为
(2) 统计集合预测序列检验。同样对1998—2007年独立样本进行检验,统计集合预测序列的趋势预测准确率为
10年的独立样本检验结果显示:第一,“第n+1年”预测和统计集合预测的趋势预测准确率都是
样本数n=47时,第n+1年(即2008年)北疆夏季降水指数预测值为110.3 (图 3)。进一步分析入选的4个环流因子与北疆降水指数的单相关系数以及2008年对应的前期环流因子值(表 4),都定性地支持降水指数值偏低的预报结果。对比北疆夏季降水指数异常偏少年的前期环流因子临界值以及2008年的因子值(表 4),有3个因子支持2008年北疆夏季降水指数异常偏低,即偏少值在50以上。统计集合预测序列中2008年北疆夏季降水指数预测值为106.9。综合以上分析,预测2008年夏季北疆地区降水偏少,区域降水指数为106.9,偏少量在40以上,出现异常偏少的概率较大。
3 讨论与结论(1) 使用滑动相关—逐步回归—集合预测相结合的方法建立模型,总样本数n= 47时,得到的北疆夏季降水指数的拟合(预测)序列与原始序列之间的相关系数为0.7248。经综合分析比较,最终的统计集合预测效果最好,预测2008年北疆夏季降水将偏少,降水指数为106.9,偏离正常值40以上。
(2) 总样本数n=47时,结果显示,北疆夏季降水指数与前一年8月到当年1月持续6个月的印缅槽指数关系密切,还与前一年12月到当年1月的印度副高脊线位置有关,同时与当年1月的南方涛动指数以及当年4月的北美副高面积指数也有密切关系。可见,前期1月的南方涛动仅仅是影响北疆夏季降水的前期显著因子之一,北疆夏季降水还同时与副热带地区广泛分布的高压和低值系统关系密切。前期印度洋到南亚地区的副高以及印度副高与西太平洋副高之间印缅槽的活动与新疆北部夏季降水异常之间的物理联系机制及其影响方式等,还需要更加深入的研究。
(3) 魏香、谭艳梅、王慧等[17-18, 20]的研究指出,前期冬、春季南方涛动指数或热带太平洋海温与新疆北部地区夏季降水关系密切。利用滑动相关—逐步回归—集合预测相结合的方法,可以从数千环流因子中挑选出与新疆北部夏季降水指数之间有显著统计关系的前期环流因子,与上述研究人员在一定物理意义基础上具有针对性的分析结果有相似之处。也从另一方面说明滑动相关—逐步回归—集合预测方法具有从大量环流因子中诊断并确定显著因子的能力。
(4) 以前一年5月至当年4月的环流指数为因子,仅仅适合5月份汛期滚动预测业务。年度预测、汛期预测的制作发布时间分别在每年的元月初和3月中、下旬,通过改变环流指数因子的起始月份可以适应这些业务的需要,如,以最新得到的月环流指数为基准,向前推得到前期12个月的环流指数作为因子即可。时间越早,大气环流对夏季降水的影响机制越复杂,不确定性增大,统计关系的显著性下降,影响预测效果。
(5) 区域季节降水指数与月环流指数都是时间序列,有自身随时间变化的规律,两者之间的相关关系随时间的变化存在不稳定性。滑动相关方法选取因子,在一定程度上考虑到了因子与因变量的时间序列特征,特别是考虑了因子与因变量之间相关关系的不稳定性。月动力产品释用技术也是目前短期气候预测业务的主要工具,李维京、林纾等[21-22] 提出的物理统计方法基于大气动力方程,侧重于统计因子的物理意义解释,但是在相关分析时,仅考虑了样本的因子与因变量之间的对应关系,没有充分考虑因子与因变量的时间序列特征。相关分析与时间序列分析相结合的方法还有待于深入探讨,但是该思路及方法可以在季节、月等不同时间尺度的短期气候预测业务中发挥作用。
致谢:感谢审稿专家的建议,感谢李维京研究员的鼓励与帮助!
张家宝, 邓子风, 1987. 新疆降水概论[M]. 北京: 气象出版社, 10-58.
|
陈兴芳, 赵振国, 2000. 中国汛期降水预测研究及应用[M]. 北京: 气象出版社, 21-64.
|
张庆云, 陶诗言, 1998. 亚洲中高纬度环流对东亚夏季降水的影响[J]. 气象学报, 56(2): 199-211. DOI:10.11676/qxxb1998.019 |
黄荣辉, 陈际龙, 周连童, 等, 2003. 关于中国重大气候灾害与东亚气候系统之间关系的研究[J]. 大气科学, 27(4): 770-787. |
赵汉光, 张先恭, 1993. 我国东部夏季雨带的气候分类及其环流特征[J]. 气象, 19(9): 3-8. DOI:10.7519/j.issn.1000-0526.1993.09.001 |
张素琴, 林学椿, 2000. 副高持续异常对长江中下游夏季降水的影响[J]. 气象, 26(5): 27-31. DOI:10.7519/j.issn.1000-0526.2000.05.007 |
程玉琴, 张少文, 徐钰强, 等, 2001. 冬季环流与赤峰地区夏季旱涝[J]. 气象, 27(11): 44-46,56. |
许炳南, 2001. 贵州夏季严重旱涝的环流异常特征[J]. 气象, 27(8): 45-48. DOI:10.7519/j.issn.1000-0526.2001.08.010 |
赵振国, 廖荃荪, 1991. 南方涛动与我国夏季降水[J]. 气象, 17(6): 33-37. DOI:10.7519/j.issn.1000-0526.1991.06.006 |
龚道溢, 2003. 北极涛动对东亚夏季降水的预测意义[J]. 气象, 29(6): 3-6. DOI:10.7519/j.issn.1000-0526.2003.06.001 |
赵振国, 廖荃荪, 1992. 冬季北太平洋涛动和我国夏季降水[J]. 气象, 18(2): 11-16. DOI:10.7519/j.issn.1000-0526.1992.02.002 |
王健, 2000. 新疆夏季降水偏多(少)同期环流特征分析[J]. 新疆气象, 23(6): 3-5. |
王娇, 任宜勇, 2005. 新疆降水与环流场演变研究[J]. 干旱区研究, 22(3): 326-331. |
杨莲梅, 张庆云, 2007. 新疆北部汛期降水年际和年代际异常的环流特征[J]. 地球物理学报, 50(2): 412-419. |
张友姝, 史玉光, 张恒德, 等, 2007. 新疆夏季降水异常的时空特征及北极涡与阻塞高压对其的影响[J]. 干旱区地理, 30(6): 879-887. |
魏香, 陈菊英, 2002. 新疆北部降水的气候分布特征及其对ENSO的响应[J]. 地球物理学进展, 17(4): 753-759. |
魏香, 陈菊英, 2002. 新疆北部雨季降水对ENSO的响应[J]. 气象, 28(9): 22-27. DOI:10.7519/j.issn.1000-0526.2002.09.005 |
谭艳梅, 2001. 新疆季降水与太平洋海温的相关分析[J]. 新疆气象, 24(5): 9-12. |
施能, 魏凤英, 封国林, 等, 1997. 气象场相关分析及合成分析中蒙特卡洛检验方法及应用[J]. 南京气象学院学报, 20(3): 355-359. |
王慧, 王铁, 陈洪武, 1999. El Nino和La Nina事件与新疆月气温降水的关系[J]. 新疆气象, 22(4): 21-24. |
李维京, 张培群, 李清泉, 等, 2005. 动力气候模式预测系统业务化及其应用[J]. 应用气象学报, 16: 1-11. |
林纾, 李维京, 陈丽娟, 2004. 月动力延伸预报产品在甘肃省的使用及评估[J]. 气象, 30(10): 22-26. |
 2009, Vol. 35
2009, Vol. 35