引言

在业务部门的台风降水预报中，路径数值预报是一个很重要的参考依据。如果单纯依靠路径数值预报而过早地预报台风降水，则有可能导致预报失败。2005年9号台风麦莎北上过程中北京暴雨预报的落空就是一个典型的例子^[1]。

“麦莎”于2005年7月31日12时(世界时, 下同)在菲律宾以东洋面上生成，8月2日00时加强成为强热带风暴，2日18时发展为台风，5日19时40分在浙江省台州市玉环县登陆，登陆时中心最低气压为950hPa，近中心最大持续风速45m·s^-1，“麦莎”的登陆在沿海地区造成了强降水^[2]。“麦莎”登陆以后继续向西北方向移动，强度逐渐减弱。7日00时在江苏和安徽交界处开始转向东北，12小时后基本上向北运动。8日06时进入渤海后路径再次发生转折，开始向东和东北方向运动，并于8日23时10分在辽宁省大连市龙王塘镇再次登陆，登陆时中心最低气压为995hPa，近中心最大持续风速12m·s^-1，“麦莎”变为热带低气压并逐渐消失，整个过程约为200小时。

“麦莎”的路径数值预报，尤其是登陆后的北上路径趋势，各预报中心分歧较大。“麦莎”登陆后路径发生了两次突然转折。第一次是7日00时在安徽突然折向江苏。第二次是在渤海转向东北。8月6日在“麦莎”行至安徽省境内时，欧洲中心预测“麦莎”将在渤海湾上西移，日本则预测台风将东移。在这种情况下，气象部门倾向于欧洲中心，预报“麦莎”将于8—9日正面袭击北京，北京地区将降暴雨，局部将有100mm以上的大暴雨。一时间，京城如临大敌。京郊4万人待命转移，17座病险水库空库迎汛，1000辆公交救援客车紧急待命，地铁做好了临时封站、短时停运的准备，卫生部门紧急发布汛期水污染预警……此外，北京市还调整成立了72个防汛指挥部，全市动员防汛抢险队伍30万人，其中驻京部队3.5万人，专业抢险队伍100多支。首都北京全城严阵以待。然而，“麦莎”却减速并在渤海湾转向了东北，实际的降水开始时间明显偏晚，过程降水量也显著偏少^[1]。于是天气预报的可信度在京城百姓的心中变为一个大大的问号。李津等^[1]总结了此次暴雨预报失误的原因，一个重要因素就是过早地依赖路径数值预报。那么，路径数值预报在这个个例中的可信度到底怎么样呢？

一般来讲，大气的可预报性是指大气中有多少成分是可以预测的以及确定性预测的时效有多长。大气和其它不稳定动力系统一样，其可预报性是有限的，即使在模式完美无缺和初始条件近乎完全正确的条件下也是如此^[3]。大气的可预报性是随尺度变化的，对波数小于40的波长而言，大气的可预报性为2周左右^[4]；由于中尺度模式中存在着复杂的不同尺度间的相互作用，其误差的增长机制还不是十分清楚。中尺度系统的可预报性问题仍是一个尚未解决的问题。1994年，肖天贵等^[5]利用1949—1987年10~45°N、100~170°E范围内1402条台风路径，对不同季节、不同地理区域、正常路径和异常路径，比较系统地分析了西北太平洋台风路径的可预报性问题，指出台风路径的可预报时间尺度:异常路径为1~2天，正常路径为3~5天。Aberson和Samson 2002年的研究也证实了这一点^[6]。本文试图通过确定性和集合预报试验对台风麦莎路径在渤海折向东北的可预报性作初步的探讨。

1 模式、资料和方法

所用模式为宾夕法尼亚州立大学和美国国家大气研究中心联合研制的非静力中尺度模式MM5第三版本。模式水平方向格点数为120×190，中心点在38°N、115°E，垂直方向27层，格距为30km，物理参数化方案包括Grell积云对流参数化方案，霰(Reisner2)云物理方案，ETA Miller-Yamada行星边界层方案。模式初始场和边界采用1°×1°的NCEP全球预报系统GFS的最后分析资料(FNL)。

集合预报初始集合通过MM5三维变分方法来产生^[7]。MM5三维变分方法通过极小化分析场与观测和背景场的距离来得到最佳分析场。为了误差极小化计算上的简便，模式变量首先转换为误差不相关的控制变量。MM5的控制变量包括流函数、速度势、非平衡气压和比湿。利用MM5三维变分方法来产生扰动，基本思路是把一组随机产生的控制变量通过经验正交函数和递归滤波转换为模式变量。由于三维变分采用的是增量形式，产生的模式变量增量与扰动基本场叠加就形成了扰动集合样本^[7-8]。具体来讲，首先遵从平均值为零、标准偏差为1的正态分布随机产生一组控制变量，然后随机控制变量通过经验正交函数分解和递归滤波转换回模式空间，风和气压平衡部分的扰动量通过线性平衡方程由流函数和势函数求出。总气压的扰动为平衡和非平衡两部分的和。温度的扰动由静力学方程得到。其它变量如垂直速度、云水、雨水、雪水和软雹混合比不做扰动。由于控制变量是随机产生的，重复N次该计算过程即可得到N个样本。这样产生的集合的样本方差是可调的。为了估计台风路径预报的可信度，所用的扰动标准偏差在观测误差范围之内。风的标准偏差约为1m·s^-1，温度的标准偏差约为1K。

集合预报样本数的选择目前来讲没有一个固定的标准，从理论上讲，样本数越多越好。考虑到集合的合理性以及计算条件的限制，本文集合样本数为20。

2 数值试验和结果分析 2.1 确定性预报试验

确定性预报是指单一模式的预报。在确定性预报中，预报模式对不同的物理过程采用某一可选的次网格物理过程参数化方案。各种物理过程参数化方案的不确定性是模式误差的一个重要来源。

积云对流参数化实质上是反映湿对流的统计效果以得到一个闭合的天气预报系统，在中尺度模式中积云尺度和中尺度之间较小的能谱差距使积云对流参数化问题面临很大的困难^[9]，因而成为中尺度数值预报最大的误差来源^[10]。积云对流参数化方案一般包括对流触发机制、闭合假定和云模式三个方面。对这三个方面不同的处理形成了多种不同的方案。MM5有7种方案可供选择，在此选取两种隐式描述对流过程的对流调整方案[Anthes-Kuo (“Kuo”)和Betts-Miller (“BM”)]和两种利用云模式直接模拟对流过程的质量通量方法[Kain-Fritch (“KF”)和Grell]。Kuo和BM方案是把不稳定大气往一个稳定的参考大气温度和湿度廓线调整，不考虑对流的具体结构，因而也就不包含下沉气流。Grell和KF方案则显式地考虑对流结构，因而包含下沉气流。

利用这四种不同的积云对流参数化方案，对模式分别从6日12时、7日00时和7日12时作72、60和48小时的积分到9日12时来考察不同积云参数化方案和不同的预报时效对台风在渤海湾转向的模拟效果。台风的模拟路径(图 1)表明, 对48小时的预报而言, 四种不同的积云参数化方案对台风的路径影响比较类似，模拟台风在渤海均转向东北向胶州半岛移动。当预报时效延长至60小时时，各方案出现了比较大的分歧。对流调整方案即Kuo和BM方案的预报与其48小时的预报比较接近。而显式描述对流的Grell和KF方案的模拟台风转向了西北偏北，60小时的路径预报误差接近500km。72小时的预报与60小时的预报结果类似。这些模拟结果表明，台风在渤海湾的转向在48小时以上时效的预报误差较大。“麦莎”在渤海湾转向东北可能仅有两天的可预报性。Kuo和BM方案对“麦莎”渤海转向的可预报性要大于两天。

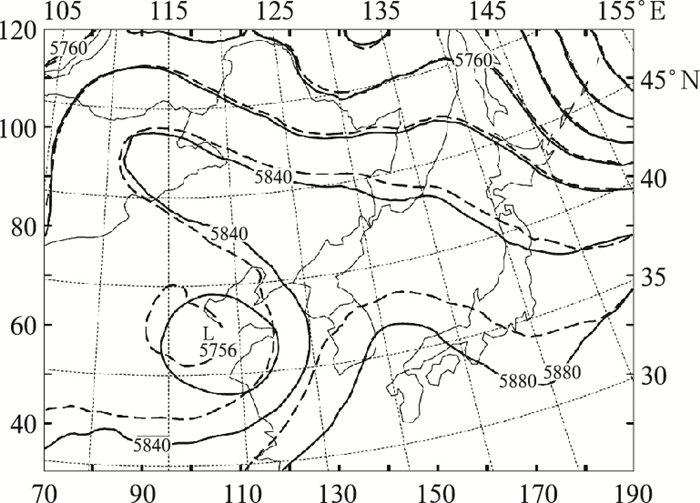
为了进一步研究不同时效和不同方案所得到的不同路径的原因，分析了各试验在8日12时台风正处于向东北转向的转折点上时的500hPa位势高度的分布特征，发现KF和Grell方案中副热带高压伸展范围明显比Kuo和BM方案的偏西偏北(图 2)，因而在其引导下台风的路径获得了更多的西北分量。

以上结果表明，时效为60和72小时的不同的积云参数化方案的模拟结果分歧较大。虽然事后分析表明Kuo和BM的结果比较接近台风的实际路径，然而实际业务预报中如何判断哪一个预报更可信呢？检查集合预报的发散度就是一种比较有效的方法。

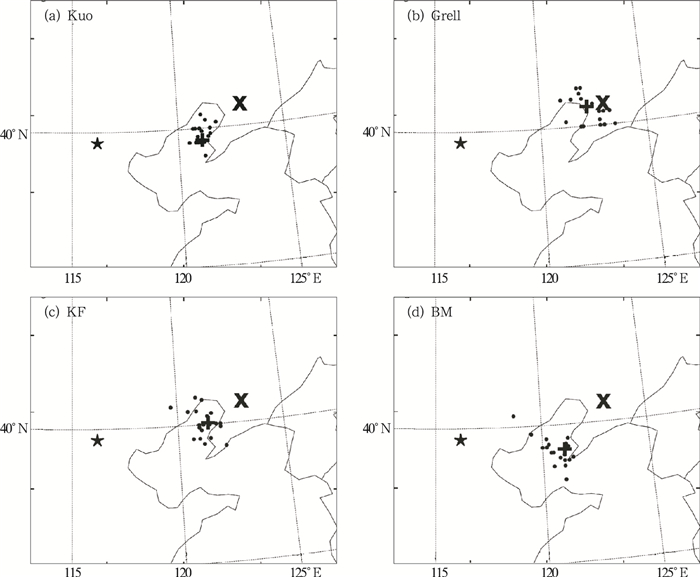
2.2 集合预报试验

利用第1节所述的方法，以6日12时、7日00时和7日12时的美国NCEP最后分析资料FNL为基础，分别产生了20个样本的集合，并分别积分72、60和48小时。图 3给出了始于7日12时积分到9日12时四种积云参数化方案的所有集合样本的48小时模拟台风的中心位置分布图。可以看到，所有方案都报出了台风向东北的转向。预报位置都比较集中，四个方案的发散度或位置标准差都小于100km，其中Kuo方案的48小时集合预报位置标准差仅为45km。另外，四种方案中所有的样本都位于集合平均位置的大约200km以内，北京显然是个离群点。因而“麦莎”不太可能直接影响北京。该结果表明麦莎在渤海湾的转向可以提前48小时做出较为准确的预报。

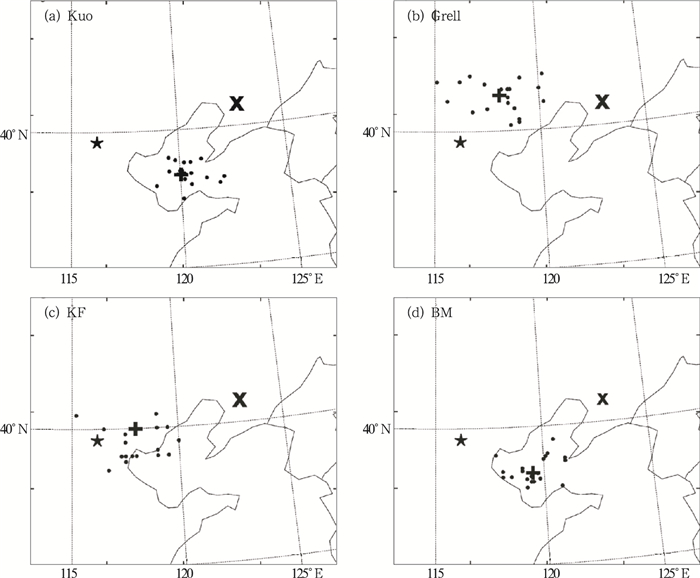
当预报时效延长至60小时(图 4)，所有四种方案的9日12时的预报位置的发散度都有所增加。Grell和KF方案增加了将近一倍(表 1)，都大于120km。Kuo和BM方案的发散度略有增加，但仍然小于100km。这说明Kuo和BM方案的预报可信度要高于Grell和KF方案。Kuo和BM方案60小时预报集合平均位置虽比48小时偏南，但仍模拟出了向东北的转向，北京的位置依旧明显在集合之外。而Grell和KF方案的60小时集合预报却偏向了西北方向，北京的位置已和其外围样本的模拟台风位置没有什么区别，也就是说北京已包含在集合预报范围之内，台风有了直接影响北京的可能。类似的特征同样可以从始于6日12时的72小时预报结果(图略)中看到。

本节的试验结果进一步证明，就路径走向而言，Kuo方案的模拟效果最好, 且可信度比较高。同样基于对流调整的BM方案的模拟效果仅次于Kuo方案。这两种方案均预示“麦莎”影响北京的可能较小。另外两种显式云模式方案的60和72小时的模拟台风路径比较偏向西北方向，但可信度不大。根据48小时各方案的一致性预报可以看出，“麦莎”在渤海湾的右折的可预报性仅为两天左右，与肖天贵等^[5]的观测研究结果一致。

3 结论和讨论

(1) 利用不同的积云参数化方案对台风麦莎路径的模拟有着明显的不同。在这个个例中，Kuo和BM两种对流调整方案的模拟效果好于Grell和KF方案。

(2) 集合预报结果表明，在这个个例中，Grell和KF方案样本的预报位置发散度比Kuo和BM方案的大，因而Grell和KF方案的预报可信度低于Kuo和BM方案，而且其可信度随预报时效的增加迅速减小。Kuo和BM方案的发散度随时效增加变化不明显，其可信度比较大而且稳定。

(3) 北京对Kuo和BM方案的任何时效的集合位置来讲都是一个离群点，对Grell和KF方案的48小时的预报也是一个离群点。因而如果做两天以内的预报，“麦莎”基本不会直接影响北京。60和72小时的预报结果Kuo和BM方案中台风仍转向东北，而Grell和KF方案中台风表现出直接影响北京的可能性，但其可信度低于Kuo和BM方案的结果。

总而言之，“麦莎”在渤海湾的右折可预报性约为两天。实际业务预报中需要考虑的因素很多，作为首都的北京市关系重大，这使得预报员在预报决策中尤其要慎重考虑。提前60~72小时预报“麦莎”可能影响北京是有依据的，但是基于本来就有很大不确定性的路径预报之上的降水预报不确定性更大，如果能够根据后期的形势预报加以调整效果会好很多^[1]。

最后想要指出的是，不能仅凭着一个个例试验的结果而得到Kuo和BM方案的结果好于Grell和KF的普遍结论。不同积云参数化方案的效果还和模式分辨率的高低以及所研究的天气系统有着密切的关系。另外，通过对台风向东北或西北转向的原因分析比较初步，下一步计划通过资料同化手段对“麦莎”在渤海的折向机制作进一步的研究。