引言

在建立气象经济模型的时候，为了能更准确地揭示气象因子对经济的影响，要考虑其他因子的影响，诸如资本、能源、劳动力等因子，因为这些因子相对于气象因子来说对经济的影响更为重要。在气象经济研究领域，这方面现有的研究要么避开考虑其他因子的作用采用问卷调查^[1]、层次分析法^[2]等方法，要么就是基于应用广泛且比较成熟的生产函数，如美国开展了规模较大的“美国不同经济行业对天气敏感性评估项目”^[3]，通过构造生产函数模型来揭示行业的天气敏感性，模型主体考虑了资本、劳动力、能源和气象因子(气温、降水)的耦合。丑洁明等^[4]通过构建一个引入气候因子的生产函数模型，研究了气候变化对粮食产量的影响，其中考虑的影响粮食产量的其他主要因子为农业劳动力、粮食作物播种面积和化肥施用量。吴先华等^[5]利用C-D生产函数模型, 在考虑销售收入、资本投入等因素的基础上分析了气象异常指数对我国典型工业产业的影响及弹性。这些研究印证了只有综合考虑各种影响因子的作用才能够较为准确地揭示出气象因子的实际影响作用。但是这些方法的局限在于，得到的气象因子对经济的影响结果是一个平均值，由于实际经济活动极易受到当时政策、灾难等突发因素的影响，所以研究因子间的相互动态影响就显得更有意义，结构向量自回归模型(SVAR)就是计量经济学中揭示因子间相互动态影响的主流方法之一。

应当指出基于SVAR模型的研究最初应用在宏观经济领域，首次提出该方法的Blanchard等^[6]，就用它研究了美国宏观经济波动的凯恩斯解释；最近Patricia等^[7]分析了实际供给与需求对股价的冲击影响。国内的研究不多见，主要集中在货币^[8]和财政^[9]政策的影响方面。本文将其应用拓展到气象经济领域，一方面是考虑到气象因子对经济的影响类似于政策因子，都不是直接影响经济系统的最根本因素，但是的确对经济都有影响；另一方面是本着引进主流计量经济学方法研究气象经济的思路，所以我们尝试运用基于SVAR模型的方法来探讨气温因子对工业经济的动态影响。

大量的研究证明，改革开放以来我国的经济增长依赖于新古典经济增长理论所强调的资本、劳动力等因素，因此我们建立的SVAR模型，引入资本和劳动力因子，加上工业经济和气温因子，是一个四元的SVAR模型，然后采用脉冲响应函数来考察气温对工业经济的动态影响，并用方差分解法揭示其相互影响程度。

1 数据收集及准备

本文采用气温序列来表示气候变暖，用南京市的工业产值来表征工业经济, 用南京市的GDP表示资本因子，用南京市大中型企业的科技人员数表示劳动力因子，这是基于有效劳动力的考虑，实际上包含了技术进步对工业经济的影响。通过查阅历年的《南京统计年鉴》^[10]，基于数据可得性(主要受统计口径变化影响，以及尽可能减少不同历史时期政策变动导致的相关影响)，得到了1986—2006年21年的数据序列。对其中的价格序列按照《中国统计年鉴2007》中的价格定基指数，求得以2006年价格为基准的可比价格序列。鉴于产值序列是年际数据，因此采用南京站1986—2006年的年平均气温序列。然后为消除数据的异方差，对这些数据都做了取对数处理, 记为工业产值(LNI)、资本因子(LNGDP)、劳动力因子(LNS)、气温因子(LNT)。

2 方法介绍及分析 2.1 SVAR模型及其建立

向量自回归模型(VAR)是Sims^[11]首次提出的一种用非结构性方法来建立各个变量之间关系的建模方法。VAR模型中每一变量都表示为其自身和其他变量滞后的回归方程形式，常用于预测相互联系的时间序列系统及分析随机扰动对变量系统的动态冲击，从而解释各种经济冲击对经济变量形成的影响。结构向量自回归模型(SVAR)方法的提出是基于改进VAR模型的不足^[12]：一是VAR模型存在参数过多的问题，只有所含变量较少的VAR才可以得到满意的估计结果；二是VAR模型不考虑经济理论，产生的冲击是一种复合冲击，产生的脉冲响应因为“新息”(异常向量)不能被识别为内在的结构误差，因而无法给出任何结构性解释。SVAR模型通过对参数空间施加约束条件从而减少了要估计的参数个数，并且能得到各变量对纯冲击的响应情况。对于一个包含k个变量，p阶的结构向量自回归模型SVAR(p)可以表示为：

$ \begin{array}{l} {\mathit{\boldsymbol{B}}_0}{\mathit{\boldsymbol{y}}_t} = {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_0} + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1}{\mathit{\boldsymbol{y}}_{t-1}} + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_2}{\mathit{\boldsymbol{y}}_{t-2}} + \cdots + \\ \;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_p}{\mathit{\boldsymbol{y}}_{t-p}} + {\mathit{\boldsymbol{u}}_t}, t = 1, 2, \cdots, T \end{array} $

(1)

(1) 式中，下标t表示时间, p表示滞后阶数,Γ₀, …，Γ_p, 分别为常数项向量和各滞后变量的系数矩阵, B₀为内生变量当期系数矩阵,y_t-p为各内生变量向量，u_t是分别作用在各内生变量上的结构式冲击，即结构式残差。然后主要通过AIC(Akaike Information Cr iterion)信息准则^[12]和SC(Schwarz Criterion)信息准则^[12]确定最佳滞后阶数，这里取2，因此首先建立包含LNI、LNGDP、LNS、LNT 4个因子的SVAR(2)模型：

$ {\mathit{\boldsymbol{B}}_0}{\mathit{\boldsymbol{y}}_t} = {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_0} + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1}{\mathit{\boldsymbol{y}}_{t-1}} + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_2}{\mathit{\boldsymbol{y}}_{t-2}}\mathit{\boldsymbol{ + }}{\mathit{\boldsymbol{u}}_t} $

(2)

其中变量和参数矩阵为:

$ \begin{array}{l} {\boldsymbol{y}_\boldsymbol{t}} \boldsymbol{=} \left[{\begin{array}{*{20}{c}} {LNI}\\ {LNGDP}\\ {LNS}\\ {LNT} \end{array}} \right], {\mathit{\boldsymbol{B}}_0} = \left[{\begin{array}{*{20}{c}} 1&{{b_{12}}}&{{b_{13}}}&{{b_{14}}}\\ {{b_{21}}}&1&{{b_{23}}}&{{b_{24}}}\\ {{b_{31}}}&{{b_{32}}}&1&{{b_{34}}}\\ {{b_{41}}}&{{b_{42}}}&{{b_{43}}}&1 \end{array}} \right], \\ \;\;\;\;{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_0} = \left[{\begin{array}{*{20}{c}} {{b_{10}}}\\ {{b_{20}}}\\ {{b_{30}}}\\ {{b_{40}}} \end{array}} \right], {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1} = \left[{\begin{array}{*{20}{c}} {\alpha 11}&{\alpha 12}&{\alpha 13}&{\alpha 14}\\ {\alpha 21}&{\alpha 22}&{\alpha 23}&{\alpha 24}\\ {\alpha 31}&{\alpha 32}&{\alpha 33}&{\alpha 34}\\ {\alpha 41}&{\alpha 42}&{\alpha 43}&{\alpha 44} \end{array}} \right], \\ \;\;\;\;\;{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_2} = \left[{\begin{array}{*{20}{c}} {{\beta _{11}}}&{{\beta _{12}}}&{{\beta _{13}}}&{{\beta _{14}}}\\ {{\beta _{21}}}&{{\beta _{22}}}&{{\beta _{23}}}&{{\beta _{24}}}\\ {{\beta _{31}}}&{{\beta _{32}}}&{{\beta _{33}}}&{{\beta _{34}}}\\ {{\beta _{41}}}&{{\beta _{42}}}&{{\beta _{43}}}&{{\beta _{44}}} \end{array}} \right], {\mathit{\boldsymbol{u}}_t} = \left[{\begin{array}{*{20}{c}} {{u_{1t}}}\\ {{u_{2t}}}\\ {{u_{3t}}}\\ {{u_{4t}}} \end{array}} \right] \end{array} $

(2)

如果B₀矩阵可逆，可将式(2)转化成如下简化式：

$ \begin{array}{l} {\boldsymbol{y}_\boldsymbol{t}} \boldsymbol{=} \mathit{\boldsymbol{B}}_0^{-1}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_0} + \mathit{\boldsymbol{B}}_0^{-1}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1}{y_{t-1}} + \\ \;\;\;\;\;\;\mathit{\boldsymbol{B}}_0^{ - 1}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_2}{y_{t - 2}} + {\mathit{\boldsymbol{\mu }}_t}, {\mathit{\boldsymbol{\mu }}_t} = \mathit{\boldsymbol{B}}_0^{ - 1}{\mathit{\boldsymbol{\mu }}_t} \end{array} $

(3)

对于k元p阶SVAR模型，需要对结构式施加k(k-1)/2个限制条件才能识别出结构冲击。由于本文的模型中包含4个内生变量，即k=4，所以需要对模型施加6个约束条件才能识别出结构冲击。我们根据各因子影响经济的实际状况和一般经验，作出如下6个短期约束，即假设B₀矩阵中各对应的当期系数值(第1期的响应值):

(1) 气温短期内对劳动力因子没有影响，即B₀矩阵中b₃₄=0。

(2) 劳动力因子短期内对气温没有影响，即b₄₃=0。

(3) 资本用来投资，对工业产值有直接的影响，但是这里用GDP表示资本，所以同期的GDP是不可能马上用于投资的，基于此假设资本短期内对工业产值没有影响，即b₁₂=0。

(4) 同样资本短期内对劳动力亦没有影响，即b₃₂=0。

(5) 工业经济对气温有影响，但短期内影响忽略不计，即b₄₁=0。

(6) GDP对气温有影响，但短期内影响同样忽略不计，即b₄₂=0。

如此，我们建立的四元SVAR(2)模型的结构式就可以识别了。

采用最小二乘法估计如式(3)所示模型，调整后的拟合优度值平均为0.97，说明模型拟合效果较好，F统计值平均为77.13，说明模型总体显著。为节省篇幅仅给出我们关心的工业产值(LNI)和气温(LNT)的估计方程：

$ \begin{array}{l} LNI = 1.68LNI(-1)-0.35LNI(-2) - \\ 0.66LNGDP( - 1) + 0.15LNGDP( - 2) + \\ \;\;\;\;0.50LNS( - 1) + 0.11LNS( - 2) - \\ \;\;0.76LNT( - 1) + 0.93LNT( - 2) - 3.52 \end{array} $

(4)

$ \begin{array}{l} LNT = 0.20LNI(-1)-0.42LNI(-2) - \\ \;0.42LNGDP( - 1) + 0.76LNGDP( - 2) - \\ \;\;\;\;0.15LNS( - 1) + 0.0014LNS( - 2) - \\ \;\;0.62LNT( - 1) - 0.63LNT( - 2) + 5.74 \end{array} $

(5)

2.2 SVAR模型的检验

由于SVAR模型的分析结果严格依赖于随机扰动项为白噪声序列这一假设条件, 因此我们首先要对模型的数据序列进行协整检验。先应用ADF方法对各序列及其1阶差分序列进行平稳性检验, 结果见表l。可见各序列的1阶差分均在5%的显著性水平以上通过检验，说明各序列均为1阶差分平稳的，即各序列均为1阶单整序列。

接着采用Johansen协整检验^[12]来检验模型是否存在协整关系，其结果显示在5%的显著性水平下至少存在1个协整方程，证明模型中各内生变量之间具有协整关系，说明这些因子组成的经济系统, 具有长期的均衡关系。在短期内由于随机干扰, 这些因子可能会偏离均衡值, 但这种偏离是暂时的, 最终会回到均衡状态。检验的结果表明本文采用的数据序列是协整的, 适用于SVAR模型的分析。

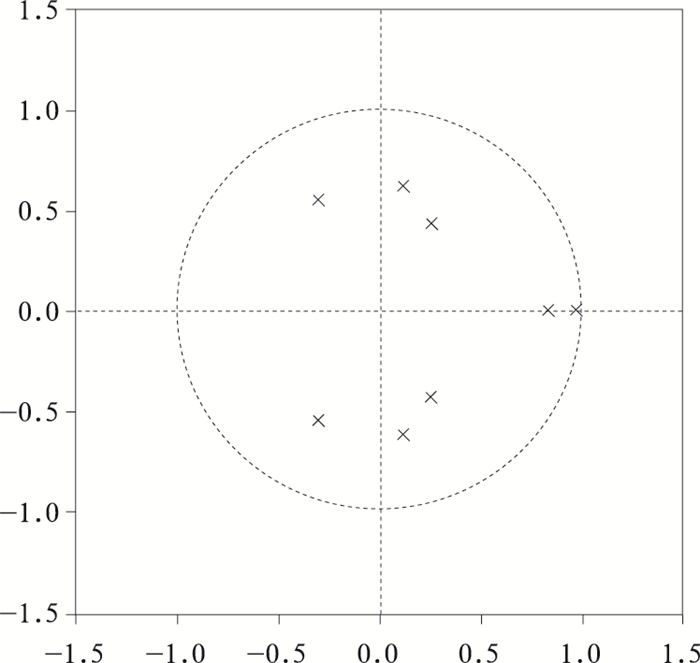
最后关键的是对SVAR模型做稳定性检验，因为模型稳定是运用脉冲响应函数分析方法的前提。如果被估计的模型中所有根模的倒数小于1，即位于单位圆内，则表示模型是稳定的。检验结果见图 1，所有单位根的模都在单位圆内，说明模型是稳定的。

2.3 脉冲响应函数分析

本文主要通过建立多变量的结构向量自回归模型(SVAR模型)来考察气温与工业产值之间的变化关系。由于VAR/SVAR模型是一种非理论性的模型，它对于变量没有任何先验性的约束，因此在分析时，往往不直接分析变量之间的影响，而是分析当一个误差项发生变化，或者说模型受到某一变量的冲击或扰动时，对模型产生的动态影响，这就是所谓的脉冲响应函数(IRF)分析方法^[12]。在SVAR模型中，脉冲响应函数反映了在一个扰动项上加上一个冲击后，对内生变量的当前和未来值带来的影响。首先我们分析工业产值对于气温的单位冲击的反应函数，其脉冲响应函数为∂y_1+s/∂u_4s，其中s是冲击作用的时间滞后期，∂y_1+s是各期的工业产值，∂u_4s是各期的气温，s的长度为10年。

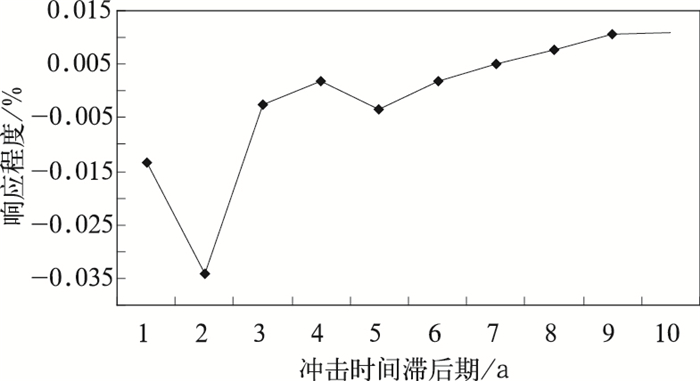
借助Eviews5.0软件计算，得到工业产值对于气温冲击的脉冲响应轨迹，如图 2所示。图中横坐标表示冲击发生后的时间间隔(年)，纵坐标表示工业产值对于气温冲击的反应程度(百分数)。可以看到除第4年外前5年工业产值对气温冲击的响应是负值，后5年的响应为正，其累计响应值为-0.016，可见整体上，工业产值对气温冲击的响应是负向的，即气温升高对南京市的工业经济带来负面影响。这个结果可以解释为，气温升高导致极端天气事件频发、气象灾害频繁，对工业的负面影响在短期内很快就体现出来，因此前5年的响应为负，而长期来看，随着企业应对气候变暖意识的加强和能力的提高，这种负面效应就会消失，所以后5年的响应转为正，但是毕竟其负面影响较大，所以总体上气温升高对工业经济的影响是负的。

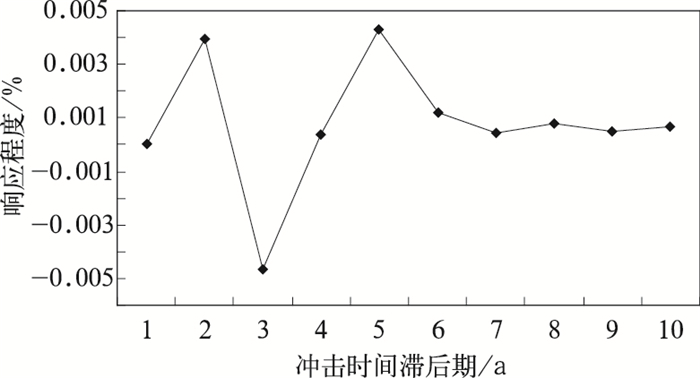
图 3是气温对于工业产值冲击的脉冲响应轨迹，除了第1年的响应为0，第3年的响应为负外，其余响应期内的响应值都为正，且其累计响应值为0.008，说明南京市的工业经济发展对当地的气温升高有正向促进作用，并且这种促进作用在长期看来是越来越明显的。原因在于南京工业经济的发展导致碳排放的增加，同时厂房、工业园区的兴建导致绿地的大量减少，使得城市热岛效应增强，所以促使南京市的气温升高。

图 2的结果与不考虑其他因子，单纯分析这两者之间关系的结果(如两变量的协整分析显示气温升高对南京工业经济有正向促进作用^[13])是截然相反的，但是图 2的结果与单纯的分析却又是一致的，都证明南京工业经济发展对气温升高有促进作用。原因在于气温因子对于行业经济发展不是主要影响因素，而行业经济发展(人类活动)对于气温的变化却是主要影响因素。这说明，当分析气象因子对于某个经济体影响的时候，单纯的不考虑其他因子影响的分析仅仅能够揭示其作为主要影响因素方面的作用，只有同时考虑了该经济体的其他主要影响因素才能准确地揭示出该气象因子影响作用的大小。

2.4 方差分解

为定量分析南京市气温与工业经济之间的相互影响程度，我们运用方差分解法来做进一步探讨。方差分解法是将系统的预测均方误差分解成系统中各变量冲击所做的贡献, 从而可以考察任意一个内生变量的预测均方误差的分解。

取有限的s项，本文的方差分解模型^[12]为:

$ \begin{array}{l} RV{C_{j \to i}}(\mathit{s}) = \frac{{\sum\limits_{q = 0}^{s- 1} {{{\left[{\mathit{c}_{ij}^{(q)}} \right]}^2}{\sigma _{jj}}} }}{{\sum\limits_{j = 1}^k {\left\{ {\sum\limits_{q = 0}^{s - 1} {{{\left[{c_{ij}^{(q)}} \right]}^2}{\sigma _{jj}}} } \right\}} }}, \\ \;\;\;\;\mathit{i}, \mathit{j} = 1, 2 \cdots, \mathit{k} \end{array} $

(6)

其中，c_ij^(q)是第j个变量对第i个变量冲击的脉冲响应函数，σ_jj是第j个变量的标准差，如果RVC_j→i(s)大，说明第j个变量对第i个变量的影响大。

表 2给出方差分解结果，其中第2列反映了气温冲击对南京市工业产值的贡献率，除第2、3期比较高外，其余时间滞后期内贡献都在3%以下，其平均贡献率为3.1%，说明总体平均来看每年南京市工业产值的3.1%受到气温升高的影响，由上述脉冲响应函数的分析知，这种影响是负面的。另外前期贡献率较高也反映了气温升高在短期内对工业经济的影响更大，这与上述脉冲响应函数的结果是一致的。

表 2中第3列则反映了南京市工业产值冲击对气温的贡献率，可以看到前5年的贡献明显呈增长的态势，贡献率从当期的0%增长到第5期的5%以上，第6年开始其贡献率维持在5.6%左右，平均贡献率为4.4%，说明除了全球气候变暖的大背景外，南京市工业经济的发展的确对南京市年平均气温的升高有贡献。需要说明的是其贡献率偏小，工业经济增长对气温升高的贡献每年仅4.4%，原因在于一方面南京年平均气温呈震荡上升的态势，很多年份是下降的，这就削弱了其贡献，另一方面与我们假设工业产值当期对气温没有影响(b₄₁=0)有关，从分析结果看假设一个适当的正值可能更为合理。

3 小结与讨论

本文运用计量经济学中研究经济系统动态性影响的经典方法——基于SVAR模型的脉冲响应函数分析方法和方差分解方法，研究了气温与南京市工业经济之间的相互动态影响。结果表明：

(1) 从脉冲响应函数分析的结果看气温升高短期内对南京工业经济有显著的负面影响，但是长期的影响转为正向促进作用，因此总体上气温升高对南京工业经济有负面作用，但是这种负面作用是趋缓的，同时方差分解结果表明平均每年南京工业产值的3.1%受到气温升高带来的负面影响；

(2) 脉冲响应函数分析的结果证明南京工业经济发展对当地的气温升高有促进作用。方差分解的结果显示，平均每年南京工业经济发展对气温升高的贡献为4.4%，进一步证明南京工业经济发展的确促进了本地的气温升高。

本文的研究证明基于SVAR模型的分析方法，可以定量揭示气象因子与经济体之间的动态影响，对研究和评估气象因子对经济体影响来说不失为一种可行方法。整个方法需要权衡的地方在于约束条件的假设，设定合理的约束假设是决定本方法分析结果精确程度的关键。