2. 鞍山市气象台;
3. 南京信息工程大学;
4. 民航江苏空中交通管理分局
2. Anshan Meteorological Observatory;
3. Nanjing University of Information Science and Technology;
4. Jiangsu Air Traffic Management Branch Bureau of CAAC
近百年来随着全球气候迅速变暖,极端天气事件发生频率急剧上升,由此给人类带来巨大的灾害与损失。因此对极端气温事件的研究日益引起人们的重视,众多学者研究发现[1-6]我国的极端温度事件也出现显著变化,大部分地区的低温日数也趋于减少。在中国东部, 日最高气温高于某一界限的高温日数明显减少。就全国平均而言, 近几十年日最高气温大于35℃的高温日数略呈减少, 长江中下游一些地区的下降更为显著;日最低气温小于0℃的霜冻日数减少也更显著, 下降速率约为21d/10a。我国霜冻日数减少最快的时期是1980年代中期以后。此外, 全国平均的热日和暖夜频率显著增加, 而冷日频率减少, 冷夜减少趋势更为明显。由此可见,我国极端气温事件的变化同气温一样具有明显的区域特征。因此,对我国极端气温事件的年际变化进行客观区划,研究不同区域极端气温事件的年际变化特征,掌握其年际变化规律,以便对未来极端气温事件的变化进行预测。关于气候区划方法已有很多研究成果,江志红和丁裕国[7]应用方差极大准则下的正交旋转因子分析,对我国40年标准化年降水量场序列进行客观区划。刘吉峰[8-9]等采用聚类分析和旋转主分量分析相结合的方案,对我国年最高(低)气温的年际变化型态进行地理区划。丁裕国等[10]更好地发展了这一新的学术观点,论证了CAST与REOF/RPCA用于气候聚类分型区划的理论联系。同时,也印证出CAST与PCA用于气象场分类区划具有等价性和互补性的事实。
在国际上通用极端气候指数[11-12]中选取了两种变化显著的极端气温指数也采用聚类统计检验分析和REOF相结合确定气温变化型和中心站的方法,利用我国多年极端气温资料,对我国极端气温变化及其特征分区进行探讨,这对国家和各级政府的规划决策具有重要的意义。
1 资料和方法 1.1 资料采用全国550个测站年最高气温和最低气温(1961—2000年)资料作为基本研究对象。选取了Firch[11]提出极端气候指数中的暖夜指数(TN90),热浪指数(HWDI), 具体的计算方法详见http://ccma/seos.uvic.ca/ETCCDMI,并利用EOF方法对两种指数的空间变化进行时空变化的特征分析,同时通过REOF和CAST方法对指数进行分区研究。
1.2 极端指数定义暖夜指数就是最低气温通过90%阈值气候态分布的天数百分率。
| $T{n_{ij}} > T{n_{in}}90 $ |
其中Tnij为某日极端最低气温,Tnin90为最低气温90%的分位数值[13]。热浪指数是指连续5天最高气温高于气候态相同日期(1961—1990年)5℃的总天数。
1.3 聚类统计检验所谓CAST聚类,就是具有显著性检验标准的聚类分析。一般可有两种计算方案:均匀聚类和中心聚类。对于地理空间上的气候区划来说,用中心聚类方案更适合。
设任意两站某项气候指标(如极端气温)的年代表值分别为xi和xj其中i=1, 2, …, p和j=1, 2, …, p, 它们实际是气候变量场中每个变量的样本取值。设rij为两者的线性相关系数, n为其样本容量, dij为两站之间的距离系数, dij={2n(1-rij)}1/2。根据文献[15]构造服从自由度为η-1的χ2分布的统计量, 得
| ${\chi ^2} = 2{\rm{n}}{\sum\limits_{\mathit{i} < \mathit{j}} {\left( {\sqrt {1 - {\mathit{\gamma }_{\mathit{ij}}}} - \hat c} \right)} ^2}{\mathop{\rm var}} \left( {{\mathit{d}_{\mathit{ij}}}} \right), $ | (1) |
| $\hat c = \sum\limits_{\mathit{i} < \mathit{j}} {\left( {\frac{{\sqrt {1 - {\mathit{\gamma }_{\mathit{ij}}}} /{\mathop{\rm var}} \left( {{\mathit{d}_{\mathit{ij}}}} \right)}}{{\sum\limits_{\mathit{i} < \mathit{j}} {^1} /{\mathop{\rm var}} \left( {{\mathit{d}_{\mathit{ij}}}} \right)}}} \right)} , $ | (2) |
| $\mathit{\eta = }\frac{1}{2}\mathit{p}\left( {\mathit{p} - 1} \right), $ | (3) |
式中η实际上就是式(1)中求和的项数, 而p则为同类样品中变量的个数。聚类统计检验方法, 就是依据式(1)~(3)逐一计算出相应的χ2统计量, 并检验零假设H0;
| ${\chi ^2} \ge \chi _{1 - a}^2\left( {\mathit{\eta } - 1} \right), $ | (4) |
如若:
| ${\chi ^2} < \chi _{1 - a}^2\left( {\mathit{\eta } - 1} \right), $ | (5) |
则表明该测站可归于同类区域。计算过程中采用逐步增加站点的方法[13]。当站点增至
| $\chi _{实}^{2}\left( \eta \right)<\chi _{1-a}^{2}\left( \eta -2 \right), $ | (6) |
且有:
| $\chi _{实}^2\left( {\eta + 1} \right) \ge \chi _{1 - a}^2\left( {\eta - 2} \right), $ | (7) |
则表明该区域所包含的η+1个站点已经足够, 不能再增加, 由此就可以确定该区域的大致边界。
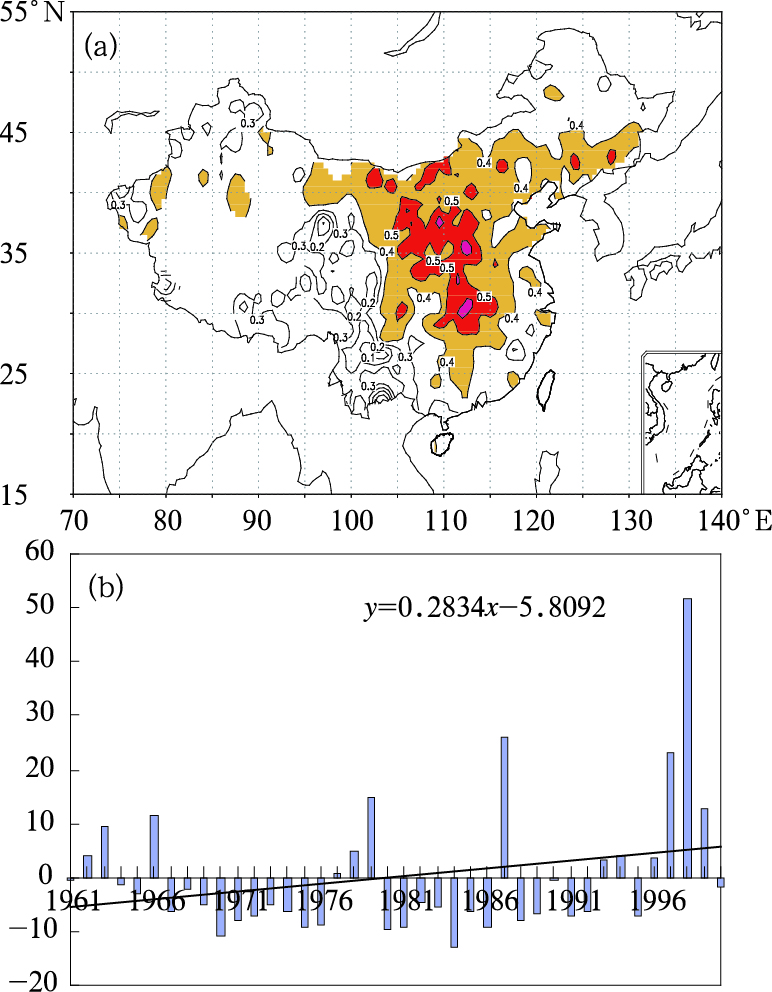
2 空间结构和时间演变特征 2.1 热浪指数的空间结构和时间演变特征热浪指数第一特征向量的方差贡献为27.1%,其相应的荷载场空间分布如图 1a,可以看出其主要的变化特征:全国呈一致增加变化,其中我国中部是荷载的高值区,而东部和西部的荷载值比较小。由第一特征向量相应的时间系数演变曲线及其线性趋势代表了高荷载区近40年来热浪指数的变化呈明显上升趋势,通过了0.05显著性水平。其中在1960年代中期到1970年代中期,1980年代热浪指数均处于低值区,其中1970年和1975年是热浪指数最低的年份。1980年代后期开始热浪指数明显增加,其中1987年和1998年,热浪指数达到最高值。
|
图 1 热浪指数的第一个特征向量空间分布(a)及时间系数演变曲线图(b) |
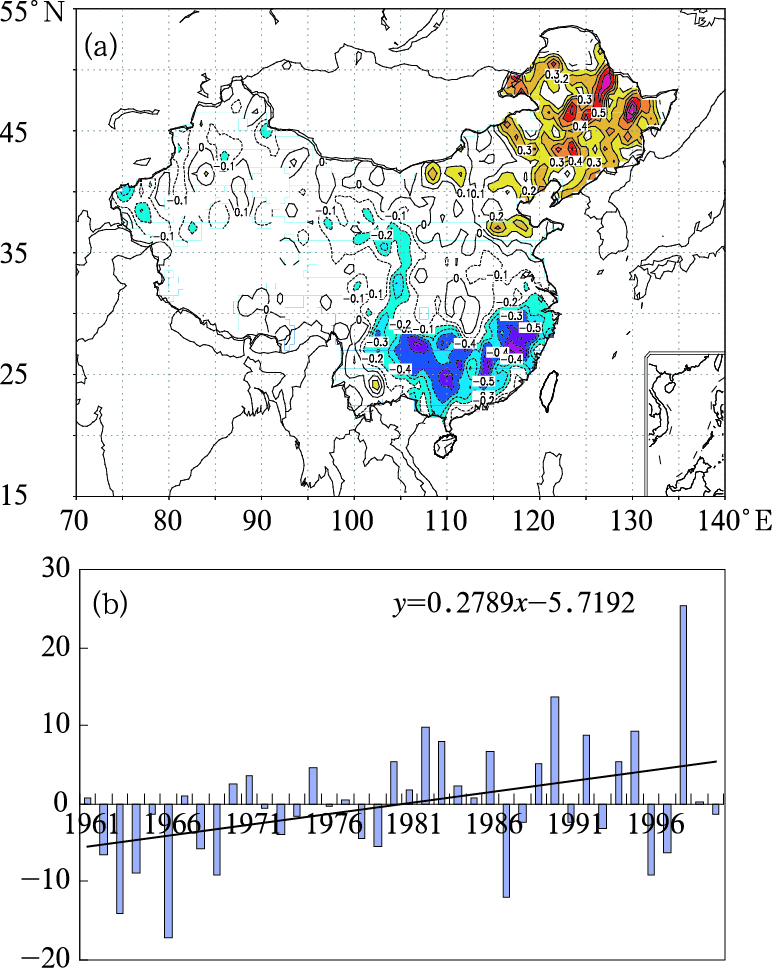
热浪指数第二特征向量的方差贡献为11.1%。其相应的空间分布如图 2a,可以看出其主要的变化特征:东北地区为正值区,而负值区在华东南部和华南北部地区为负值区,体现了北高南低的变化特征,也就是热浪指数在我国北方和南方呈相反变化。由第二特征向量相应的时间系数演变曲线及其线性趋势,我国北部和华东、华南呈一致的增加(减少趋势)。其中1970年前我国东北地区和华东、华南地区分别处于高值(低值)区,其中1961年、1966年东北地区(华东、华南)热浪指数为最低(高年份),而1980年之后,东北地区(华东、华南)热浪指数处于高值(低值区),1987年和1998年为东北地区(华东、华南)的高(低)值年。
|
图 2 热浪指数的第二个特征向量场空间分布(a)及时间系数演变曲线图(b) |
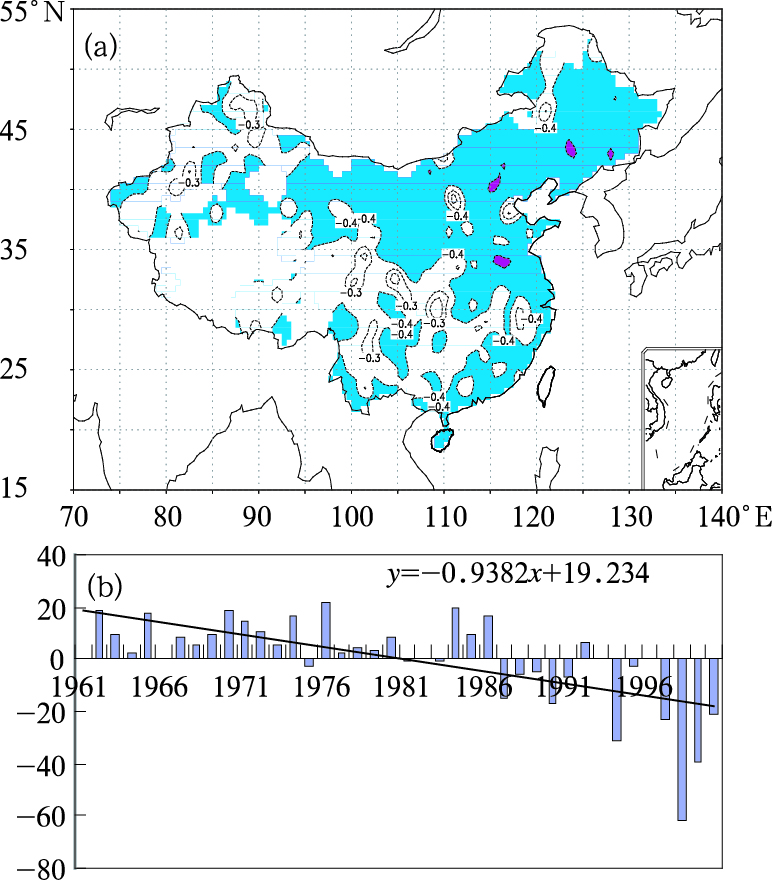
Tn90的第一特征向量的方差贡献为50.8%。其相应的空间分布如图 3(a),可以看出其主要的变化特征:全国呈一致的负变化,负值的高荷载区在东北,华北到内蒙古的西部,和华中地区。通过第一特征向量相应的时间系数变化曲线及其线性趋势。近40年来我国大部分地区暖夜指数呈明显上升趋势,并且通过了0.05显著性水平检验。在1980年代之前全国暖夜指数基本处于低值区,暖夜指数的最低年份是1967年、1970年。1980年代之后,全国的暖夜指数基本处于高值区,最高的年份处于1997年和1998年。
|
图 3 Tn90的第一个特征向量场空间分布(a)及时间系数变化曲线图(b) |
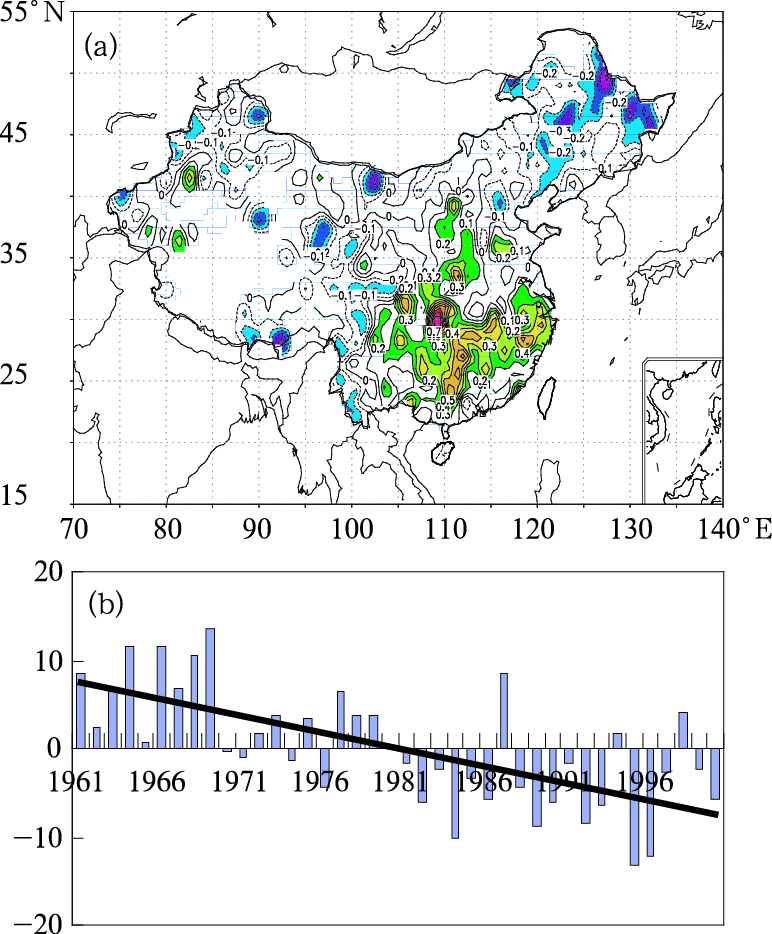
暖夜指数的第二特征向量的方差贡献为7.9%。其相应的荷载场空间分布如图 4(a),可以看出其主要的空间分布特征:我国北部和西部为负值区;华中、华南和华东为正值区,主要的高荷载区在我国东南部。由第二特征向量相应的时间系数演变曲线及其线性趋势线发现。近40年来我国东南部暖夜指数呈明显下降趋势。1980年代以前我国东南地区暖夜指数处于高值区,最低值位于1970年,在1980年代之后暖夜指数下降,在1995年和1996年出现最低值。
|
图 4 Tn90的第一个特征向量空间分布及时间系数变化曲线图 |
首先利用暖夜指数和热浪指数EOF分析的结果,分别选取前11和10个特征向量进行旋转EOF分析,由于篇幅原因,文中略去特征向量的空间分布图,只对结果进行分析。如图 5和表 1所示。

|
图 5 中国热浪指数分区 |
|
|
表 1 热浪指数前11个主要特征向量的方差贡献百分率 |
热浪指数第一特征向量高荷载区位于福建省和江西省,这一部分占方差贡献的11.73%。最大值中心位于石城附近。
第二特征向量的高荷载区位于内蒙古中部,这一部分占方差贡献的9.76%。最大值中心位于乌海附近。
第三特征向量的高荷载区位于吉林省和辽宁的东北部。这一部分占方差贡献的7.96%。最大值中心位于抚顺附近。
第四特征向量的高荷载区位于山东、江苏和安徽省的北部,这一部分占方差贡献的5.98%。最大值中心位于徐州附近。
第五特征向量有两个高荷载区,一个位于重庆和四川东部,另一个为于青海省和西藏。这一部分占方差贡献的5.38%。最大值中心一个位于内江附近,另一个位于玉树附近。
第六特征向量的高荷载区位于新疆西部,这一部分占方差贡献的4.33%。最大值中心位于喀什附近。
第七特征向量的高荷载区位于黑龙江省,这一部分占方差贡献的4.32%。最大值中心位于绥化附近。
第八特征向量的高荷载区位于新疆西北部,这一部分占方差贡献的3.88%。最大值中心位于准葛尔盆地附近。
第九特征向量的高荷载区位于云南西部,这一部分占方差贡献的3.83%。最大值中心位于思茅附近。
第十特征向量的高荷载区位于广西和贵州,这一部分占方差贡献的3.60%。最大值中心位于桂林附近。
第十一特征向量高荷载区位于西藏地区大部,这一部分占方差贡献的2.23%。
综上所述热浪指数可划为十一个区,分别位于福建和江西省、内蒙古中部、吉林省和辽宁的东北部、山东省、江苏和安徽的北部、重庆和四川东部、青海省、新疆西部、黑龙江省、新疆西北部、云南西部和广西和贵州、西藏大部。
暖夜指数第一特征向量高荷载区位于黑龙江和吉林,这一部分占方差贡献的17.77%。高值中心位于松原附近。
第二特征向量高荷载区位于广东和福建,这一部分占方差贡献的11.26%。高值中心位于河源附近。
第三特征向量高荷载区位于江苏和安徽,这一部分占方差贡献的9.14%。高值中心位于合肥附近。
第四特征向量高荷载区位于甘肃,这一部分占方差贡献的6.20%。高值中心位于白银附近。
第五特征向量高荷载区位于新疆西北部,这一部分占方差贡献的5.88%。高值中心位于乌鲁木齐西部。
第六特征向量高荷载区位于广西和湖南南部,这一部分占方差贡献的5.48%。高值中心位于桂林附近。
第七特征向量高荷载区位于山西、内蒙古中部、陕西北部,这一部分占方差贡献的4.85%。高值中心位于河套附近。
第八特征向量高荷载区位于四川和云南西部,这一部分占方差贡献的4.70%。高值中心位于保山附近。
第九特征向量高荷载区位于青海和西藏的西部,这一部分占方差贡献的2.50%。高值中心位于都兰附近。
第十特征向量高荷载区位于新疆西部,这一部分占方差贡献的2.46%。高值中心位于喀什附近。
|
|
表 2 暖夜指数前10个主要特征向量的方差贡献百分率 |
综上所述暖夜指数可划为十个区,分别位于黑龙江和吉林、广东和福建、江苏和安徽、甘肃、新疆西北部、广西和湖南南部、山西、内蒙古中部、陕西北部、四川和云南西部、青海和新疆西部。
由于有了REOF的分区,可以对这个分区结果进行聚类检验,并选取REOF旋转的最高值做为中心聚类的中心点,进行聚类的原则是:(1)选择某一中心聚类的站点数超过5个,且在地域上连成一片的可以划分为同一个极端气温区。(2)以同一站为中心若有地理上不连续的两块或以上符合条件(1)的区域,则将其分为不同的气温区。(3)假设某一中心站周围的测站少于5个,则该中心站自动变为一般站,相应区域也就不存在,所聚测站按与周围区域的相似程度(相关系数大小)决定其归属。(4)对于同时归属于不同中心站的个别台站和不属于任何中心站的台站按其与周围中心站的相似程度决定其归属。这样,各气温极端区之间就有了明确的界限,便于今后做进一步的研究。
根据上述原则,将我国将热浪指数和暖夜指数分区效果进行检验并得到区结果见(图 5、图 6)。

|
图 6 中国暖夜指数分区 |
热浪指数为11个客观分区,1区,华东华南沿海地区;2区,内蒙古地区;3区,北南部地区;4区,黄淮流域;5区,西藏西部和华中北部地区;6区,新疆南部地区;7区,东北北部地区;8区,新疆北部地区;9区,西藏东部地区;10区,华中南部地区;11区,西藏地区。
暖夜指数为10个客观分区,1区,东北和华北南部地区;2区,华南沿海地区;3区,华东地区;4区,华中北部和西北的中部地区;5区,新疆北部地区;6区,华中南部地区;7区,华北北部地区;8区,西藏东部地区;9区,西藏西部地区;10区,新疆西南部地区。
对分区后的结果重新进行EOF展开发现(表 3和表 4)可以看到热浪指数和暖夜指数各区域第一主分量方差贡献率,除了热浪指数2区和9区、暖夜指数7区外,其余均大于50%,说明各区域内的变化是基本一致的,分区的效果很好。
|
|
表 3 热浪指数各区域第一主分量方差贡献率(%) |
|
|
表 4 暖夜指数各区域第一主分量方差贡献率(%) |
(1) 热浪指数和暖夜指数的经验正交函数展开(EOF)结果表明,前2个模态基本代表了极端气温指数的空间分布特征。热浪指数和暖夜指数的第一特征向量的荷载场空间分布基本一致,全区为一致的增加和减少趋势,只是高荷载区位置不同。
(2) 利用REOF对热浪指数和暖夜指数分别进行分析,并通过聚类统计检验,确定边界的站点所在的区域,将热浪指数和暖夜指数分别分为11个和10个变化区。
(3) 通过EOF再次展开发现,将旋转主分量分析和聚类统计检验相结合用于气候区划,既克服了前者确定荷载值界限的主观性,又避免了后者选择气候中心的不确定性,使区划结果更具有客观性。
| [1] |
姚愚, 李晓鹏, 闫丽萍, 等. 近44年云南年平均气温的时空变化特征[J]. 气象, 2006, 32(10): 81-87. |
| [2] |
任国玉, 初子莹, 周雅清. 中国气温变化研究最新进展[J]. 气候与环境研究, 2005, 10(4): 702-716. |
| [3] |
向辽元, 陈星. 近55年中国大陆气温突变的区域特征和季节特征[J]. 气象, 2006, 32(6): 44-47. DOI:10.7519/j.issn.1000-0526.2006.06.007 |
| [4] |
赵宗慈. 近39年中国的气温变化与城市化影响[J]. 气象, 1991, 17(4): 14-17. DOI:10.7519/j.issn.1000-0526.1991.04.003 |
| [5] |
丁一汇, 戴晓苏. 中国近百年来的温度变化[J]. 气象, 1994, 20(12): 19-26. DOI:10.7519/j.issn.1000-0526.1994.12.008 |
| [6] |
唐国利, 林学椿. 1921—1990年我国气温序列及变化趋势[J]. 气象, 1992, 18(7): 3-6. DOI:10.7519/j.issn.1000-0526.1992.07.001 |
| [7] |
江志红, 丁裕国. 近40年我国降水量年际变化的区域性特征[J]. 南京气象学院学报, 1994, 17(1): 73-78. |
| [8] |
刘吉峰, 李世杰, 丁裕国, 等. 一种用于中国年最高(低)气温区划的新的聚类方法[J]. 高原气象, 2005, 24(6): 966-973. |
| [9] |
刘吉峰, 李世杰, 丁裕国, 等. 近几十年我国极端气温变化特征分区方法探讨[J]. 山地学报, 2006, 24(3): 291-297. |
| [10] |
丁裕国, 张耀存, 刘吉峰. 一种新的气候分型区划方法[J]. 大气科学, 2006, 31(1): 129-136. |
| [11] |
Frich, P., 1999: REWARD-A Nordic Collaborative Project. Annex of "Meet ing of the Joint CCl/CLIVAR Task Group on Climate Indices, Bracknell, UK, 2-4 September 1998, Folland, C. K., Horton, E. B. and Scholefield, P. R. (Eds), World Climate Data and Monitoring Programme, WCDMP-No. 37, WMO-TD No. 930. WMO (1999).
|
| [12] |
Alexander L.V, Zhang X, Peterson T.C. Global observed changes in daily climate extremes of temperature and precipitation[J]. Geophys. Res, 2006, 111: 1-22. |
| [13] |
Zhang X, G Hegerl, F.W Zwiers. 2004: Avoiding inhomogeneity in percentile-based indices of temperature extremes[J]. J. Climate, 2005(18): 1642-1651. |
| [14] |
魏凤英. 现代气候统计诊断与预测技术[M]. 北京: 气象出版社, 1999.
|
| [15] |
刘吉峰, 李世杰, 丁浴国, 等. 一种用于中国最高(低)气温区划的新的聚类方法[J]. 高原气象, 2005, 24(6): 966-973. |
 2008, Vol. 34
2008, Vol. 34