2. 中国气象局国家气候中心气候研究开放实验室;
3. 水利部淮河水利委员会水文局;
4. 水利部水文局
2. Laboratory for Climate Studies, National Climate Center, China Meteorological Administration;
3. Huaihe River Commission;
4. Bureau of Hydrology, Ministry of Water Resources
GCM(大气环流)模式被广泛用来研究气候变化,进行气候模拟和预测。而目前的GCM是粗分辨率模式,无法模拟细分辨率的陆表面特征量。早期许多学者[1-5]在研究中提出次网格降水空间变率对陆表面能量通量、土壤湿度和径流等有显著影响。Entekhabi[1]提出,降水和土壤湿度的次网格空间变率极大改善了GISS-GCM对径流和蒸发的模拟。为了更准确描述降水在陆面水文过程中的分配,必须考虑降水的次网格特性。
一般一个GCM网格内的降水等大气强迫项在网格区域内是平均分配的,因此忽视了降水非均匀性带来的陆面水文的变化及对地表热量平衡各分量的影响,从而影响陆面气象要素次网格尺度不均匀性分布。
Warrilow等[2]指出降水集中在网格中间的一个区域内,降水量满足指数分布形式,
| $ f({{P}_{i}})=\frac{\mu }{{{P}_{m}}}\text{exp(}\frac{\mu {{P}_{i}}}{{{P}_{m}}}\text{)} $ |
Pm是GCM在格点内产生的平均降水,μ是降水在格点内覆盖的比例。这种指数分布形式认为在每个次网格降水分布都是一样的,满足指数分布,忽略了降水在各个雨站分布是不均匀的。
利用这种指数分布形式,许多研究者研究大气强迫降水对陆面水文的影响。Xu Liang[6]两层渗入量模式,在模式中也考虑了降水的次网格变率,用解析的一维统计动力表示降水的部分覆盖面积,这种方法考虑次网格空间降水变率对得到准确的表面通量、径流和土壤湿度的影响。把结果同降水在网格内均匀分布的结果比较,发现在网格内降水的覆盖面积在模拟表面通量、径流和土壤湿度是扮演了一个重要的角色。AndreaN.Hahmann[7]描述GCM中次网格降水变率,引入这种降水指数分布分离方案,模拟的气候和格点内降水均匀的结果有很大不同。
虽然在以往的研究中,研究者们应用降水的指数分布研究取得了一定成果,然而众多的研究和观测事实表明,降水空间分布是不均匀的,也不是呈指数分布的。pitman[8]研究表明,改进某个地区降水分布能够改变径流和蒸发之间的平衡,到目前为止还没有一种合适的分布函数可以很好描述降水的次网格特征[9]。Gao.X[10]研究了美国三个区域的降水空间分布变率,提出降水分布既不是均匀的,也不是指数分布的,而是具有非均匀性质的统计模态,Gao.X[10]提出了一种降水随机分离方案,模拟降水在次网格内的分布,方案可以模拟降水在次网格的分配,模拟结果较好。
本文在Gao.X的降水离散分布方案的基础上,根据淮河流域降水的统计特征,在东亚地区找到在一个格点区域降水覆盖面积的PDF(概率密度分布函数),实现降水随机分配。
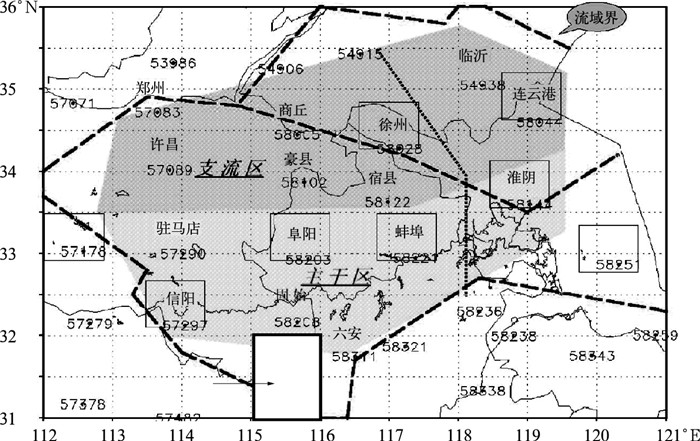
1 资料HUBEX(淮河流域试验)是全球能量与水分循环试验/亚洲季风试验在东亚副热带半湿润地区开展的气象、水文观测试验。淮河流域的外场观测试验提供了大量的地面、探空、水文、辐射等多种加密和特殊的观测资料。本文利用实验成果中的加密观测降水及其后长时间降水逐小时观测资料,研究淮河流域降水空间分布的特点。淮河流域位于31~36°N、112~12 1°E的范围内[11-12]。在淮河流域选择一块区域,具体位于31~32°N、115 ~ 116°E,见图 1。图 1是淮河流域平面图,图中箭头所指区域就是研究区域范围,其中包括了32个站点逐小时降水加密观测资料,水文加密自记雨量站分布非常集中,这有利于研究在一个格点内存在次网格降水不均匀分布特征。经过整理的降水资料,1998年观测时间从5月21日到8月31日,1999年观测时间从5月1日到8月31日,2001年至2003年取观测时间从6月1日至8月31日。32个站点若有站点出现降水时,就当作一次降水事件,6年共2532个降水事件。
|
图 1 站点分布位置 |
区域内常年逐小时降水观测资料可以分布在一个时间和站点标号的平面内(图略),当区域中任一站点在一小时内出现降水,就认为是一个降水事件,如果某个站点出现2小时连续降水,就认为是2个独立的降水事件。对应每个站点,每次事件都有降水强度(mm·h-1), 这样32个站点逐小时的降水序列可以构成时间-空间上的矩阵。矩阵内不是0的元素代表降水强度I(mm·h-1),空白代表没有降水。定义每次降水事件,降水覆盖的面积占整个格点区域面积的比值为:
| $ N\left( t \right)=\sum\limits_{i=1}^{n\left( t \right)}{{{W}_{i}}=S\left( t \right)/A} $ | (1) |
定义每次降水事件,每小时降水平均强度为:
| $ Z\left( t \right)=\sum\limits_{i=1}^{n\left( t \right)}{[I\left( t, i \right){{W}_{i}}]} $ | (2) |
Wi(=Si/A)是站点i占的面积权重。在本文中站点i的面积权重Wi假设相等。
另外把格点区域分成若干个相等的次网格小区域,每个站点都位于这个小区域的中心,我们可以设想,如果观测站点分布得足够密,当站点出现降水时,则这个小区域都充满降水,在这种假设下,每小时降水量V,和它的覆盖面积S,能够表示为:
| $ S\left( t \right)=\sum\limits_{i=1}^{n\left( t \right)}{{{S}_{i}}}=A\sum\limits_{i=1}^{n\left( t \right)}{{{S}_{i}}/A}=A\sum\limits_{i=\text{ }1}^{n\left( t \right)}{{{W}_{i}}} $ | (3) |
| $ V\left( t \right)=\sum\limits_{i=1}^{n\left( t \right)}{[I\left( t, i \right){{S}_{i}}]}=A\sum\limits_{i=1}^{n\left( t \right)}{[I\left( t, i \right){{W}_{i}}]} $ | (4) |
n(t)是在事件t出现降水的站数,A是格点的面积,从以上4个式子得到关系式:
| $ Z\left( t \right)/N\left( t \right)=V\left( t \right)/S\left( t \right) $ | (5) |
从式(5)看出,如果从实际观测的逐小时降水资料得到Z和N的关系,就可以得到格点内V和S的关系。当大气环流模式输出一个格点内平均降水强度时,按照长期降水资料得到的降水覆盖面积的PDF曲线,在这种PDF下计算机随机数产生器可以产生相应的降水在格点区域内的覆盖面积。根据6年降水资料统计得到每个站降水概率,利用随机概率分配,可以得到在哪些站点降雨,将格点内平均降水强度分配给随机程序得到的降雨站点。
3 淮河区域降水分布统计特征淮河流域32个水文站分布在31~32°N、115~116°E内的很小范围内,如果在在格点内观测的降水平均降水强度一定时,降水分布面积和发生频率满足固定的分布形态,则认为在GCM中,降水在一个格点内分布满足的模态。每个站点的降水都是从1998年到2003年夏季逐小时出现降水的观测资料。表 1的统计结果表明,在长期的降水事件中,区域平均降水强度在0.1mm内的降水事件占总降水事件的63.1%,而且平均降水强度超过9.0mm区域内,降水事件只有两次。利用公式(1)和(2)N和Z的计算,计算1998—2003年夏季逐小时降水序列每次降水事件时的N和Z,统计每年和6年累计(图略)当降水平均强度Z变化时,出现降水的站点占所有台站的比例不同,表明在一个格点内降水分布是不均匀的,在有降水事件时,有的站点出现降水,有的站点没有降水或者各个站点降水量也不同。在平均降水强度超过1mm区域内,出现降雨的站明显增多,在平均降水强度达到9.5mm和13.6mm时,整个区域站点均出现降水。
|
|
表 1 1998—2003年淮河流域夏季降水事件统计 |
在一次降水事件发生时,降水在陆表面覆盖的面积S和平均降水强度N之间有明显的近似线性关系(图略),我们可以得到7条曲线,6条曲线分别是1998—2003年夏季N和Z之间关系,一条是统计6年降水资料得到的Z和N之间的关系。可以看出7条曲线形态相似,且曲线集中在一个窄小的范围内。表明6年中每一年数据反映的关系和6年反映的平均降水强度和分布面积的关系模态相似,当平均降水强度增大则降水在陆表面覆盖面积也增大。降水事件发生时,降水覆盖面积和发生频率也可以得到7条曲线,6条曲线分别是1998—2003年夏季N和发生频率之间关系,一条是统计6年降水资料得到的N和发生频率之间的关系,7条曲线都表明,当降水覆盖面积增加,可能发生的频率迅速减少,说明降水最容易发生在格点区域一个非常小的部分。
1998—2003年每一年和6年降水在陆表面覆盖的面积S和平均降水强度N的关系,以及降水在陆表面覆盖面积N和发生频率之间关系非常相似,因此本文从6年总降水事件统计6年降水在陆表面覆盖面积N和发生频率的PDF,将降水强度分成不同小段,得到在不同降水强度间隔降水覆盖面积的PDF(图略)。这意味着强度和面积之间的关系可能可以分成有限个模态。根据降水强度在不同分布面积的发生频率的时间分布(图略),我们选取不同强度间隔。降水在区域强度小于0.1mm时,发生的频率最大,发生降水事件最多。降水强度在0.0~0.1mm时降水发生频率随分布面积呈近似的指数分布,一个明显的特征是降水分布在很小范围内的可能较大。当区域降水强度超过0.1mm时,PDF基本呈现两峰型,并随着降水强度增大,峰值右移,即降水平均强度变大,覆盖面积较大的可能性增加[13]。
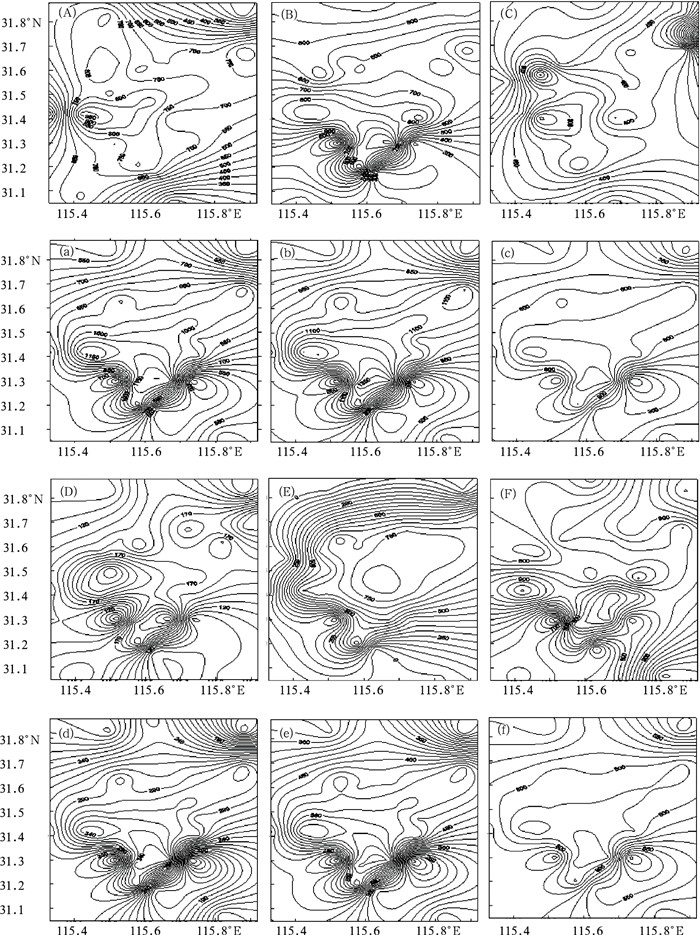
4 淮河流域降水试验结果由淮河区域降水分布统计特征可以明显看出,每年区域内降水空间分布及6年区域平均降水空间分布非常相似,因此可以利用6年总降水事件得到区域平均降水强度和降水覆盖面积PDF,实现格点区域内降水随机分配。将不同降水强度的PDF输入计算机,当GCM输入一个降水强度V时,根据PDF概率分布模态,计算机可以随机分配降水在格点内的覆盖面积,从而可以得到有几个站点降雨。根据6年统计得到每个站降水概率(图略),利用随机概率分配,可以得到在哪些站点降雨,从而将平均降水强度V分配给降雨站点。区域平均降水强度超过9.0mm以上的降水事件只有两次,降水强度分别为9.5 mm和13.6mm,在这两次降水事件中区域内所有站点都观测到降水,由降水在陆表面覆盖的面积S和平均降水强度N之间的近似线性关系得到结论,平均降水强度越大,区域内降水覆盖面积也越大,即出现降水的站点越多,所以在本文的降水分离方案中假设平均降水强度超过9.0mm时,则认为区域内所有站点都出现降水。本文模拟6年降水分布图和实况,可以看出降水离散方案根据降水概率分布关系模拟出的降水空间分布形势(图略)与实际降水空间分布(图略)几乎一致,只是在降水量级上仍旧有偏差。图 2是降水分离方案对每一年模拟得到的结果,右列是观测结果,左列是模拟结果。结果表明,模拟降水空间分布形势与站点实际观测降水空间分布形势非常相似,方案可以模拟出降水量较大的地区,模拟出的降水量值有偏差但差别不大。由于在研究区域6年降水统计特征相似,降水在研究区域空间分布也比较相似,造成模拟出6年降水空间每一年降水空间分布相似。
|
图 2 1998年—2003年降水方案模拟与观测结果比较
(A)、(B)、(C)、(D)、(E)、(F)分别代表 1998、1999、2000、2001、2002、2003年模拟值 (a)、(b)、(c)、(d)、(e)、(f)分别代表 1998—2003年观测值 |
利用HUBEX科学成果及加密水文站长期的降水观测资料,可以得到淮河流域降水在空间分布是不均匀的,长期降水资料序列分析表明,当这个区域降水强度增加时,降水覆盖面积也增加。同时,表 1的统计结果表明,在长期的降水事件中,区域平均降水强度在0.1mm内的降水事件占到总降水事件的63.1%。在不同区域降水强度下,降水分布面积和发生频率满足固定的分布形态。降水发生频率在随不同覆盖面积的PDF可以用来刻画GCM中降水次网格分布。模拟的降水分离结果表明,可以利用这种降水分离方案实现GCM的次网格降水分配。淮河流域是南北气候的过渡带,淮河地区的洪涝灾害对国家和人民的财产造成很大的损失,但我们对这一地区的预报能力并不高。本文工作对于研究淮河地区降水空间分布变率,考察淮河地区降水的空间分布,提高GCM在这一地区陆面水文参数化模拟能力,提高气候模式的模拟能力有很强的现实意义。
致谢:本文在完成中曾获得气候中心张雁帮助,气候中心廖要明给了许多建议和启迪,在此表示衷心感谢。
| [1] |
Entekhabi D, Eagleson P S. Land surface hydrology parameterization for atmospheric general circulation models including subgrid scale spatial variability[J]. J. Climate, 1989, 2: 816-831. DOI:10.1175/1520-0442(1989)002<0816:LSHPFA>2.0.CO;2 |
| [2] |
Warrilow D A, A B Sangster, and A Slingo. Modeling of land-surface processes and their influence on European Climate[M]. Dynamical Climate Tech. Note, U. K. Meteorological Office, Bracknell, Berkshire, England, 1986, 92.
|
| [3] |
Pitman A J, Henderson-Sellers A, Yang Z L. Sensitivity of regional climates to localized precipitation in global models[J]. Nature, 1990, 346: 734-737. DOI:10.1038/346734a0 |
| [4] |
徐晶, 姚学祥. 流域面雨量估算技术综述[J]. 2007, 33(7): 15-21.
|
| [5] |
Wood E F. Global scale hydrology: Advances in land surface modeling[J]. U.S. Natl. Rep. Int. Union Geod. Geophys. 1987-1990, Rev. Geophys, 29, Suppl., 1991, 193-201. |
| [6] |
Liang X, Lettenmaier D P, Wood E F . A one-dimensional statistical dynamic representation of subgrid spatial variability of precipitation in the two-layer variable infiltration capacity model[J]. J. Geophys Res., 1996, 101(D16): 21403-21422. DOI:10.1029/96JD01448 |
| [7] |
Andrea N Hahmann. Representing spatial subgrid scale precipitation variability in a GCM[J]. Journal of Hydrometeorology, 2003, 4: 891-900. DOI:10.1175/1525-7541(2003)004<0891:RSSPVI>2.0.CO;2 |
| [8] |
Pitman A J, Henderson-sellers A, Yang Z L. Sensitivity of regional climates to localized precipitation in global models[J]. Nature, 1990, 364: 734-737. |
| [9] |
魏和林, 符淙斌. 下垫面非均匀性的模拟[J]. 气候与环境研究, 1997, 2: 2. |
| [10] |
Gao Xiaogang, Sorooshiian Sorooshi. A stochastic precipitation disaggregation scheme for GCM applications[J]. Journal of climate, 1994, 7: 238-247. DOI:10.1175/1520-0442(1994)007<0238:ASPDSF>2.0.CO;2 |
| [11] |
徐时进, 钱名开, 徐慧. 淮河史灌河流域水量平衡初步分析[M]. 北京: 气象出版社, 1999.
|
| [12] |
丁一汇, 张雁, 马强. 1998年夏淮河流域试验加密观测期间主要天气形势特点及其重要观测成果[M]. 北京: 气象出版社, 1999.
|
| [13] |
黄嘉佑. 气象中使用统计检验的几个问题[J]. 气象, 2005, 31(7): 3-5. DOI:10.7519/j.issn.1000-0526.2005.07.001 |
 2008, Vol. 34
2008, Vol. 34