2. 中国气象科学研究院灾害天气国家重点实验室
2. State Key Laboratory Severe Weather, Chinese Academy of Meteorological Sciences
集合预报研究中最重要的问题是如何形成初始扰动,包括初值扰动和模式扰动问题。初始扰动的质量好坏直接影响集合预报的质量。初值扰动方法[1]可划分两类:第一类是估计分析误差的概率分布,如Monte Carlo随机扰动法、时间滞后平均法和观测扰动技术。第二类是通过分析数值预报误差在相空间中的增长方向和速度,沿着预报相空间中最不稳定的方向来扰动初始条件。第二类扰动方法的原理建立在对大气的可预报性研究成果的基础上,如NCEP和ECMWF分别在全球模式中应用增长模繁殖法(BGM)和奇异向量法(SV)获得扰动初值,有效地反映了中高纬度斜压不稳定的预报不确定性。
ETKF方法是由Bishop[2]等针对适应性观测问题提出来的,最近又被用于集合预报初值扰动的生成。这种方法基于集合变换方法[3](ET)和卡尔曼滤波理论(KF),是一种次优的卡尔曼滤波方案,与其它的集合卡尔曼滤波方案不同在于ETKF方法可以直接估计出与观测网有关的预报误差协方差矩阵。2003年Wang等[4]又将ETKF方法用于集合预报初值扰动的生成,并与Breeding方法做了对比,结果表明利用ETKF方法得到的集合发散度比用Breeding方法得到的发散度更能反映预报的不确定性。由于Wang(2003年)文中介绍的方法给出集合扰动是有偏的,我们一般希望集合平均与最小方差估计得到的“大气真值"相等,故需采用集合中心化方案。2004年,Wang等[5]对比了两种不同的集合中心化方案,试验发现集合扰动中心球形对称的ETKF方法要优于常用的集合扰动正负对称法[1]。2006年Wei等[6]将ETKF方法在实际业务环境中进行试验,揭示了这种方法在业务应用中的优缺点。Harlim等[7]将LEKF(Local Ensemble Kalman Filter)理论中的局地化分析思想和ETKF理论结合,提出了LET KF理论,来解决由于集合数的限制引起的虚假相关问题。
ETKF方法作为一种集合预报初值扰动方法在区域中尺度模式(GRAPES-Meso)当中进行了试验,得到了初步的试验结论。主要内容如下:第1节简单地介绍ETKF方法产生集合扰动的原理;第2部分介绍试验设置;第3节内容为试验结果分析;第4节内容为结论与讨论。
1 ETKF理论和方法简介2003年,Wang[4]将ETKF方法用于集合预报初始扰动的生成。ETKF方法可以通过将预报扰动量乘以一个变换矩阵T(T矩阵的求解见wang[4]文中介绍)来得到分析扰动
| $ {{\mathit{\boldsymbol{X}}}^{a}}={{\mathit{\boldsymbol{X}}}^{f}}\mathit{\boldsymbol{T}} $ | (1) |
我们将集合扰动定义为集合预报场与集合预报均值的差,于是有
Xa=(x1a-xa,x2a-xa,……,xKa-xa)和Xf=(x1f-xf, xf2-xf, ……,xfK-xf)
(K表示集合数目,Xa表示分析量,Xf表示预报量)。
当集合预报的代表性较差时,利用ETKF方法估计得到的误差协方差矩阵Pa=ZfTT(Zf)T(这里
| $ x_{f}^{a}=x_{i}^{f}{{T}_{i}}{{\Pi }_{i}} $ | (2) |
| $ \text{trace}(<{{\widetilde{\boldsymbol{d}}}_{i+1}}\boldsymbol{d}_{i+1}^{\text{T}}>)=\text{trace}(\widetilde{\boldsymbol{H}}\boldsymbol{P}_{i+1}^{e}{\widetilde{\boldsymbol{H}}^{T}}+\boldsymbol{I}) $ | (3) |
其中<·>表示数学期望算子,I为单位矩阵;
在假设观测误差和预报误差不相关的条件下,公式(3)表示更新向量(innovation)、预报误差协方差和观测误差协方差三者之间的关系。取向量的迹(trace)是为了使控制预报误差的方差和集合估计的预报误差方差相等。
| $ \widetilde{\mathit{\boldsymbol{d}}}_{_{i+1}}^{T}\widetilde{\mathit{\boldsymbol{d}}}_{_{i+1}}^{{}}\approx \text{trace}(\widetilde{\mathit{\boldsymbol{H}}}\mathit{\boldsymbol{P}}_{i+1}^{e}{{\widetilde{\mathit{\boldsymbol{H}}}}^{T}}+\mathit{\boldsymbol{I}}\text{)} $ | (4) |
由于不知道ti+1时刻的
| $ \mathit{\boldsymbol{d}}_{i}^{\text{T}}{{\widetilde{\mathit{\boldsymbol{d}}}}_{i}}=\text{trace}({\mathit{\boldsymbol{\widetilde{H}}}_{\alpha }}\mathit{\boldsymbol{P}}_{i}^{e}{{\mathit{\boldsymbol{\widetilde{H}}}}^{T}}+\mathit{\boldsymbol{I}}) $ | (5) |
假设ti-1时刻的扩大因子(inflation factor)为Πi-1且已知,ti时刻的为:
| $ \mathit{\boldsymbol{ \boldsymbol{\varPi} }}{{\rm{ }}_i} = \mathit{\boldsymbol{ \boldsymbol{\varPi} }}{{\rm{ }}_{i - 1}}\sqrt {{\alpha _i}} $ | (6) |
从式(5)中可以得到αi的表达式。
| $ {{\alpha }_{i}}=\frac{\widetilde{\mathit{\boldsymbol{d}}}_{i}^{T}\widetilde{\mathit{\boldsymbol{d}}}_{i}^{{}}-N}{\text{trace}(\widetilde{\mathit{\boldsymbol{H}}}\mathit{\boldsymbol{P}}_{i}^{e}\widetilde{\mathit{\boldsymbol{H}}}\mathit{\boldsymbol{P}}_{{}}^{T})}=\frac{\widetilde{\mathit{\boldsymbol{d}}}_{i}^{T}\widetilde{\mathit{\boldsymbol{d}}}_{i}^{{}}-N}{\sum\limits_{i=1}^{K-1}{{{\lambda }_{i}}}} $ | (7) |
N表示观测点的数目,λi是Γ的对角线上的元素(i=1,…,k-1)。
于是可以得到
| $ \mathit{\boldsymbol{ \boldsymbol{\varPi} }}{{\rm{ }}_i} = \sqrt {{\alpha _1}{\alpha _2} \ldots {\alpha _i}} $ | (8) |
得到Πi以后就可以利用式(2)来得到分析扰动量,得到的分析扰动量加到控制预报场上就得到集合预报的初始场。
2 试验设置试验所选用的预报模式是全球/区域同化和预报系统(GRAPES, Global and Regional Assimilation and PrEdiction System),试验选取的区域为15~60°N、70.125~144.375°E,分辨率为0.5625°,水平格点为133×81个。控制预报的设置与上述设置一致。本次试验选取了2005年11月8—12日出现的一次降雨过程进行试验,集合预报的起始时刻为2005年11月7日12UTC,到2005年11月9日18UTC。试验用的分析系统为三维变分同化分析系统,时间窗为6小时,时间步长为600s。试验所用的观测资料均为模拟的观测资料,选取00时实际的探空观测站作为试验中所用的观测站,由分析场插值到站点得到观测值。选取分析的垂直层为3层850hPa、500hPa、200hPa;选取的分析变量为U、V、T三个变量,集合成员为15个。
3 试验结果分析 3.1 特征值分布由于ETKF方法基于卡尔曼滤波理论,因而具有卡尔曼滤波方法的一些滤波特性。ETKF方法产生集合扰动的思想和Breeding方法是类似的,这种方法的一个优点是在理想试验设置下其估计得到的分析误差的增长率是一致的。图 1为在上述试验设置下误差协方差矩阵的特征值谱分布状况。整体来看分析误差协方差矩阵的特征值谱分布还是比较一致的,这说明通过ETKF分析系统可以合理地调整集合初始扰动的增长率及分布,保证集合估计得到的误差概率密度函数的一致性。
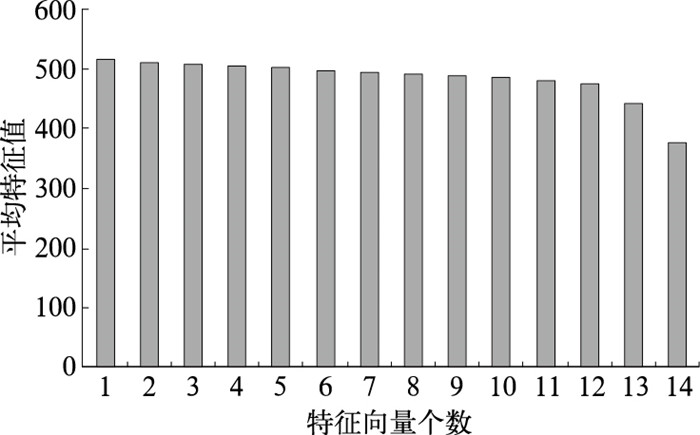
|
图 1 试验得到的分析误差协方差矩阵在观测空间的特征值谱分布 |
由于试验集合数的限制,使ETKF方法低估了部分预报误差协方差。为了弥补这方面的不足引入了扩大因子(inflation factor)来调整集合扰动的幅度。为了考察集合数的大小对扩大因子的影响,将集合数目扩大一倍进行试验。由表 1、表 2可以看出,随着集合数由15变为30,试验当中的扩大因子均值由20.64变为9.06。随着集合数增大一倍,扩大因子的数值也减少一半(20.64/9.06)。由此可以看出在集合数增大的过程中扩大因子的作用逐渐减小,这与理论上一致。
|
|
表 1 当集合数为15时,试验的扩大因子变化情况 |
|
|
表 2 当集合数为30时,试验1的扩大因子变化情况 |
为比较不同扩大因子计算方法对集合扰动变化的影响,首先利用ETKF方法得到初始扰动,然后采用两种不同扩大因子的计算方法调整集合扰动的大小。两组实验分别为:
(1) 第一组试验方案采用Wang and Bishop[4]介绍的扩大因子计算方法进行试验。
(2) 第二组实验方案是利用Breeding方法的思想计算扩大因子、调整扰动的大小。Toth和Kalnay[8]文中介绍的Breeding方法的基本思想是:将每一个预报扰动都乘以一个常数,使得到的集合扰动和根据经验得到的分析误差协方差相等:
| $ {{\mathit{\boldsymbol{X}}}^{a}}={{\mathit{\boldsymbol{X}}}^{f}}\times c $ |
Xa表示分析扰动,Xf表示预报扰动,c是一个常数即我们所需的扩大因子,在试验当中是使集合估计得到的500hPa高度上的温度方差与统计值相等得到扩大因子的数值。
由图 2可以看出试验1的500hPa高度场的扰动先增大后减少渐渐趋于一定值,图 3表明试验2的500hPa高度场扰动是缓慢增长最后趋于稳定。对比图 2和图 3可以看出两种试验方案扰动增长方式的不同。
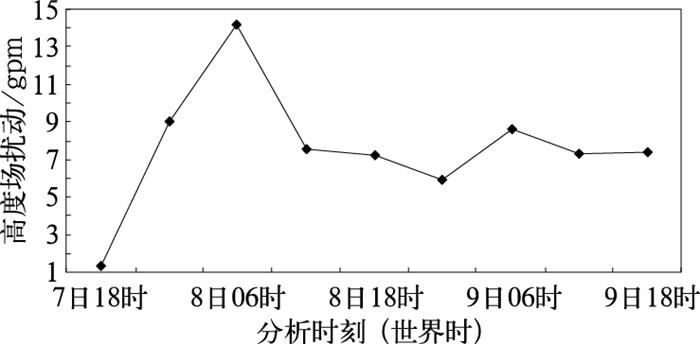
|
图 2 试验1得到的500hPa高度场扰动随时间变化情况 |
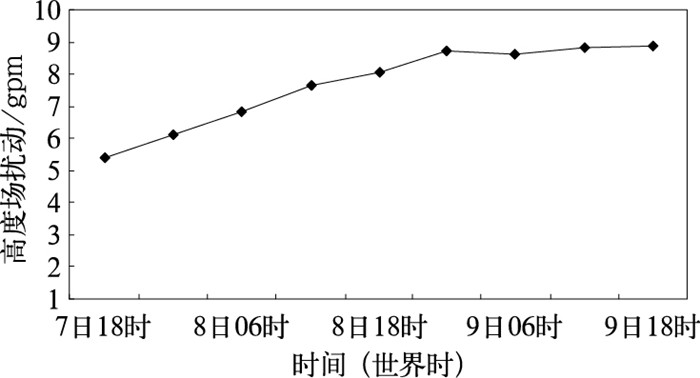
|
图 3 试验2得到的500hPa高度场扰动随时间变化情况 |
集合变换卡尔曼滤波方法区别于Breeding方法一个最大的优点是[4]在假设系统是线性,且不随时间变化、观测网的地理分布不变、观测误差固定、初始集合扰动代表线性系统误差增长的方向时,其产生的集合扰动的误差分布在彼此正交化的观测空间中的概率分布是一样的。为验证这种方法在一个随时间变化的非线性系统及有限集合数的条件下是否还可以保持其优点,利用ETKF方法进行了试验。实验结果表明对于非理想试验设置情况下ETKF方法在观测空间当中的误差特征值谱分布还是比较一致的。通过试验1和试验2的扩大因子变换情况可以看出,集合数增大的过程中扩大因子的作用逐渐减小;试验1得到的集合扰动是先增大后减小,最后趋于稳定,试验2得到的集合扰动是缓慢地增长,增大到一定程度保持不变。
目前试验当中存在的不足及改进办法:(1)ETKF系统给出的初始扰动场是由观测加扰动方法给出的,使得集合预报的初始场的发散度偏小,以后试验中这个问题可以通过其它扰动生成方法生成集合预报场来解决。(2)试验当中所用的观测值都是由GRAPES模式的分析场插值到观测站点得到,而且假设观测站点的位置不随时间变化,这与实际情况不符。在进一步试验中可以考虑引入实际观测资料进行试验。(3)试验所用的模式是区域模式,所有成员采用相同的边界条件这时边界处的发散度就为零,边界的影响会随着模式积分时间向内传播,最终影响集合预报场的质量。边界的影响可以通过扩大试验区域或者利用全球模式来克服。(4)在集合数较小的情况下,就会出现虚假相关问题,应在现用计算条件下尽可能多地引入集合预报成员。
在改善集合预报技术方面,要与数值预报其他技术的发展密切配合,协调发展。在集合预报中如何解决初始场不确定性和模式的不确定性仍将是今后研究的重点。
致谢:完成过程中得到奥地利气象局王勇博士和中国气象科学研究院数值中心的薛纪善、陈德辉等老师的热心帮助,在此向他们表示衷心的感谢!
| [1] |
田华. 国家气象中心中期集合预报概况[J]. 新疆气象, 2004, 27(5): 1-6. |
| [2] |
Bishop C. H., Etherton B. J., Majumdar S. J. Adaptive Sampling with the Ensemble Transform Kalman Filter. Part Ⅰ: Theoretical Aspects[J]. Mon. Wea. Rev, 2001, 129(3): 420-436. DOI:10.1175/1520-0493(2001)129<0420:ASWTET>2.0.CO;2 |
| [3] |
Bishop C. H., Toth Z.. Ensemble Transform and Adaptive Observations[J]. J Atmos Sci, 1999, 56(11): 1748-1765. DOI:10.1175/1520-0469(1999)056<1748:ETAAO>2.0.CO;2 |
| [4] |
Wang X, Bishop C H. A comparison between Breeding and Ensemble Transform Kalman Filter Ensemble Forecast Schemes[J]. J Atmos sci, 2003, 60(9): 1140-1158. DOI:10.1175/1520-0469(2003)060<1140:ACOBAE>2.0.CO;2 |
| [5] |
Wang X., Bishop CH, Julier S.J.. Julier. Which is better, an ensemble of positive-negative pairs or centered spherical simplex ensemble?[J]. Mon. Wea.Rev., 2004, 132(7): 1590-1605. DOI:10.1175/1520-0493(2004)132<1590:WIBAEO>2.0.CO;2 |
| [6] |
Wei Mo zheng, Toth Z., Wobus R. Wobus et al. Ensemble Transform Kalman Filter-based ensemble perturbation in an operational global prediction system at NCEP[J]. Tellus, 2006, 58A: 28-44. |
| [7] |
Jone Harlim and Brian R Hunt. Local Ensemble Transform Kalman Filter: An Efficient Scheme For Assimilating Atmospheric Data[OL]. 2005, from http://www.atmos.umd.edu/~ekalnay/harlim_hunt05.pdf
|
| [8] |
Toth Z, Kalnay E. Ensemble forecasting at NMC : The generation of perturbations[J]. Bull Amer Meteor soc, 1993, 74: 2317-2330. DOI:10.1175/1520-0477(1993)074<2317:EFANTG>2.0.CO;2 |
 2008, Vol. 34
2008, Vol. 34