2. 武汉区域气候中心
2. Wuhan Regional Climate Center
长年代连续且均一性较好的历史气象数据集是气候分析和气候变化研究的基础。由于各种原因,历史气候资料缺测现象时有发生,如湖北省1968年就有3个站共10个站月停止观测,导致这些站资料缺测,造成历史资料不连续。Stooksbury等[1]分析了日最高、最低气温记录中断(即记录缺测)对计算月平均最高、最低气温影响的时空变化规律,认为在气候变化及其趋势研究、气候评估及影响评价时要考虑数据中断的情况。
我国许多学者对月和年值时间尺度的气象资料做过缺测插补[2-7],但对日气象记录进行缺测插补尚未见文献报道。国外对日最高、最低气温短时间缺测记录插补有过研究[8-14]。Acock等[11]利用分组数据处理法对日太阳辐射、最高最低气温、风速和降水量缺测值进行了插补。Huth等[12]通过对不同天气类型建立相应的回归模型来插补缺测的日气温数据。Eischeid等[14]采用一系列空间客观插值方法,建立了美国西部1951—1991年逐日气温和降水数据集。但这些插补模型只用于一个或数个缺测日数据的插补,将其用于连续数月缺测情况(如本文讨论的蔡甸站连续3个月停止观测)并不合适。本文试图通过对线性回归模型法的一系列改进,解决这一问题。
1 资料及插补方法 1.1 资料由于历史原因蔡甸气象站1968年6—8月连续3个月停止观测导致所有气象要素缺测。为了插补该3个月的逐日最高、最低和平均气温,选取蔡甸及其周围邻近气象站孝感、汉川、江夏、武汉、云梦、应城、黄陂(其台站信息见表 1)1961—2006年逐日最高、最低和平均气温资料作为基本资料,上述资料来源于湖北省气象档案馆,且已经经过气象要素界限值、气候极值、内部一致性和时间一致性等质量控制方法的检验。
|
|
表 1 插补站蔡甸及其邻近站台站信息 |
(1) DeGaetano标准化序列法
DeGaetano等[9]利用邻近站资料对逐日最高、最低气温进行了插补,本文在应用该方法时增加了日平均气温,具体方法如下:
| $\begin{array}{l} {Z_j} = \frac{{{x_j} - {{\bar x}_j}}}{{{\mathit{S}_j}}}\\ {Z_{{\rm{avg}}}} = \frac{1}{N}\sum\limits_{j = 1}^N {{Z_j}} \\ {\mathit{x}_i} = {Z_{{\rm{avg}}}} \times {S_j} + {{\bar x}_i} \end{array} $ | (1) |
式(1)中Z表示标准化序列,j代表第j个邻近参考站,xj为日气温(即最高、最低和平均气温,下同),xj和Sj分别为日气温长期多年平均值和标准差,按照WMO规定,本文选取1971—2000年为统计基准年份(在实际缺测数据插补时,30年的基准年份应该包含缺测年份或离缺测年份最近)。N表示邻近参考站数,xi表示第i日气温记录缺测插补值,xi、Si分别是插补站第i日气温长期多年平均值和标准差。
(2) 线性回归法
利用邻近站资料,建立回归模型,插补缺测站资料的方程为:
| $\begin{array}{*{20}{l}} {{{\hat y}_i} = {a_{1i}}{x_{1i}} + {a_{2i}}{x_{2i}} + \cdots + }\\ {\;\;\;\;\;\;\;\;{a_{mi}}{x_{mi}} + {a_{\left( {m + 1} \right)i}}} \end{array} $ | (2) |
式(2)中,
| $\min \mathit{Q = }{\rm{min}}\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} $ | (3) |
利用最小二乘原理即可求解回归模型的参数(即LSE方法),式(3)中yi为插补站观测值。除了采用最小二乘法求解式(2)回归模型的参数外,也可以基于最小绝对偏差方法(即LSE方法),即:
| $\min \mathit{Q = }{\rm{min}}\sum\limits_{i = 1}^n {\left| {{y_i} - {{\hat y}_i}} \right|} $ | (4) |
由于式(4)中出现了绝对值,具有不可微性,采用最小二乘方法求解导数不可行,所以无法显式写出解线性回归模型参数的表达式。实际应用中一般通过运筹学问题中解无约束最优化问题的方法,间接估计回归模型的参数。本文通过迭代方式,利用单形调优法求目标函数的极小值方法来估计线性回归模型的参数。
1.3 误差检验方法本文采用交叉验证(cross-validation)方法对缺测记录的插补结果进行对比分析[13],即假设某个站记录缺测,利用插补模型插补日气温数据。然后对插补值与实际观测资料进行对比分析,讨论插补方法优劣和参数选取,并进行误差分析。用平均绝对误差(Mean Absolute Error,MAE)来代表插补精度。
| $MAE = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {{x_{oi}} - {x_{ei}}} \right|} $ | (5) |
式(5)中xoi为第i天实际观测值,xei为第i天插补值,N为插补天数。
2 插补试验与结果分析 2.1 时间窗大小与邻近台站数选择对缺测记录进行插补,一般采用缺测日前后邻近参考站同要素或相关要素作为样本资料,建立插补估计模型,对缺测日数据进行插补[11-14],即只对1日或数日的缺测记录进行插补,这对于本文讨论的连续数月缺测记录来说,显然不适用。为此,采用滑动优选法挑选模型样本数据,即选择缺测日前后若干天历史同期若干年(不包括缺测日所在年)的数据作为拟合回归模型的样本数据,建立线性回归模型,然后利用缺测年邻近站资料,通过该模型计算缺测记录插补值。(这样选取样本数据是合理的,因为缺测日前后几天历史同期,各要素时空变化规律通常比较相似)。如要插补1968年6月10日的最高气温,则可以选择插补站以及邻近站6月3日至6月17日1964—1972年(不含1968年)共8年每年15天的最高气温数据作为样本数据,建立回归模型,并求解模型参数,利用邻近站1968年6月10日的数据,通过回归模型,估计1968年6月10日的最高气温。选择多少年和多少日数据是通过一个时间窗来确定的。时间窗的宽度为日数,高度为年数。一般是利用以插补年为中心的前后若干年资料作为样本数据,对于前后无资料年份,使用靠近插补年份的资料。
利用多少台站对缺测记录进行插补,除与所要插补气象要素及其时间尺度、邻近站密度相关,还与插补站及其邻近站所处地理环境有关(如平原、山区等),同时时间窗大小对缺测数据插补精度有一定的影响。分别选取年数为6、8、10年,日数为11、15、19天组合成9个时间窗及邻近站数为3、4、5、6个进行对比试验,利用LAD方法,对蔡甸站1981—2000年日气温资料进行了插补试验。结果表明,随着时间窗的增大,插补误差逐渐减小,当采用4个邻近站,年数为8年,日数为15天时插补误差达到最小,当时间窗大小超过该时间窗时,误差并不减小,甚至略有增加(表 2,仅列出了部分数据)。由于蔡甸站周围基本上为平原地区,邻近参考站选取采用距离最短原则,所选4个站为武汉、汉川、江夏、孝感。
|
|
表 2 蔡甸站最高气温各月平均绝对误差MAE(1981—2000年) |
为比较LAD、LSE两种方法的插补精度,计算了蔡甸站3要素1961—2006年各月两种方法的MAE(表略)。结果表明两者平均绝对误差相差很小,由于LAD方法比LSE方法具有更好的统计性能和稳健性[13-14, 18],所以本文回归模型参数求解采用方法。
2.3 综合插补方法通过对蔡甸站1961—2006年插补试验,在±0.5℃及±0.8℃误差范围(见表 3)内,日气温3要素中LAD方法比DeGaetano方法的插补精度都高,但通过对逐日插补值的仔细分析,DeGaetano方法插补误差经常小于LAD方法。这样,能否将上述两种方法通过某种方式集成起来,以提高插补精度,降低误差。通过试验,将该两种方法的插补值的平均值作为最后插补结果,有较好效果,即综合插补方法(见表 3、表 4)。通过表 3可以看出,日气温综合方法误差在±0.5℃范围内的频率均比其他方法大,虽然增加不是非常明显,但都有增加。需要指出的是,日气温误差绝对值≥1.5℃的频次综合方法明显少于其他两种方法(表 4)。产生这种现象主要原因是,虽然DeGaetano和LAD方法,都采用相同邻近站,由于两种方法使用的样本资料大部分不相同,插补方法也不同,所以两种方法的估计值同时出现误差较大的概率就会减少,从而导致两种方法的平均值(即综合插补方法)出现误差较大的频次减少,而对误差较小的情况,综合插补方法虽有改善,但不是很明显。综上所述,综合插补方法的插补精度均优于上述两种方法,下文讨论的插补结果及其误差分析均基于综合插补方法。
|
|
表 3 蔡甸站各要素不同插补方法误差频率(%) |
|
|
表 4 蔡甸站各要素不同方法误差绝对值≥1.5℃的频次(1961—2006年) |
采用综合插补方法,利用蔡甸站及其4个邻近站1961—2006年日气温的观测值,计算蔡甸站1961—2006年插补值,利用式(5)计算MAE(由于1968年6—8月蔡甸站资料缺测,统计结果不包括该时段,下同),并统计各要素误差的频率分布(见表 3)。
由表 3可知日最高、最低和平均气温的插补误差在±0.5℃范围内的频率分别为80.3%、65.1%、85.4%,在±0.8℃频率分别达到94.1%、84.8%、96.1%,其误差绝对值大于1.0℃的分别为2.6%、8.7%、1.6%,MAE分别为0.32℃、0.45℃、0.28℃。文献[9]中日最高、最低气温插补误差75%在1.7℃范围内,最低气温MAE的为1.0℃, 最高气温的MAE为0.5℃。
为了评估本插补方法,本文插补结果分析并不限于蔡甸站数据缺测时间6—8月。按月计算观测值和插补值相关系数,统计各月最大最小相关系数并列于表 5中。由表 5可以看出,观测值与插补值各月相关系数,除最低气温有1个月为0.886外,其余都大于0.9,说明观测值与插补值的相关性非常好。
|
|
表 5 各月观测值与插补值相关系数、统计量t的最大和最小值 |
下面以月为单位讨论观测值和插补值的平均值与相关系数的显著性检验。根据文献[19],计算历年各月各要素1961—2006年平均值的统计量t,并统计最大和最小值列于表 5中。查表可知t0.05=2.0,所以插补与观测值通过了显著性水平为0.05的平均值检验,其平均值无显著性差异。根据文献[19],当自由度为26(月的最小天数为28,即n=28),相关系数大于0.478时通过显著性水平为0.01的检验,根据表 5,最小的相关系数为0.886,所以相关系数通过了显著性t检验(显著性水平为0.01)。
3 误差分析 3.1 插补误差总的来说,在3个要素中平均气温的MAE最小,最高气温居中,最低气温最大。平均气温比最高最低气温误差小的可能主要原因是,由于日平均气温是采用1天中多个时次的气温平均求得,而最高和最低气温是日极值,这样和邻近站相比日平均值变化规律通常比日极值更相似,所以用邻近站来插补缺测站的平均气温较最高最低气温误差小。最低气温比最高气温MAE大应该与它们出现的不同时间有关。李庆祥等[15]在检测气温序列中不连续点时也指出了这个问题。最低温度通常出现在日出之前,这个时候大气边界层稳定性最强,局地微气象尺度特征非常明显;而最高温度往往出现在白天,由于太阳短波辐射作用,使中小尺度范围大气边界层内大气混合充分,则不同地点气温变化差别相对较小,从而导致插补站与邻近站最高气温差别较小;而最低温度出现在大气稳定度最强时刻,此时出现的最低温度更具有局地性,导致插补站与周围站最低气温差别大,从而引起插补误差偏大。
3.2 MAE月、年际变化蔡甸站各要素MAE随月份的变化范围(图 1a),平均气温为0.22~0.37℃,最高气温为0.29~0.36℃,最低气温为0.36~0.56℃。平均气温的MAE夏半年比冬半年小;最高气温的MAE随月份的变化较小,但夏半年比冬半年稍大;最低气温变化幅度最大,其中夏半年比冬半年明显偏小。平均和最低气温的MAE夏半年比冬半年小的原因可能与冬半年是冷空气活动非常频繁的季节,由于受冷空气推进的时间和路径影响,出现了气温变化规律的时空不同步,从而导致插补站与邻近站气温差异较大。而最高气温MAE夏半年较冬半年高,可能与夏季午后局地强对流天气导致最高气温与邻近站差异较大有关。
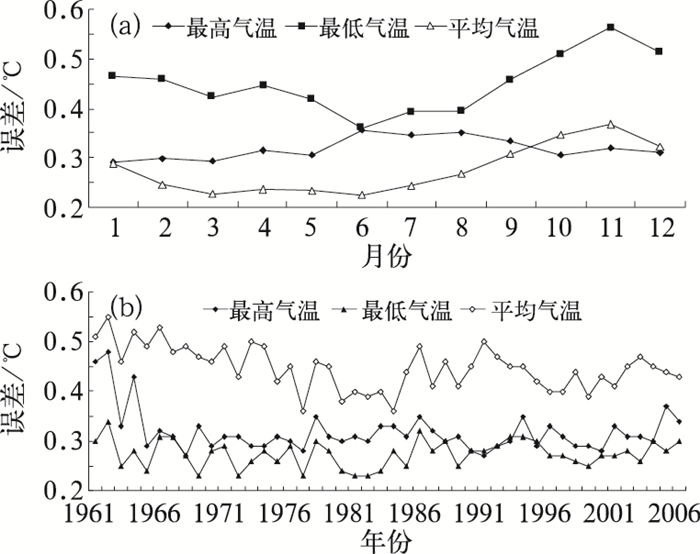
|
图 1 蔡甸站1961—2006年气温插补MAE月变化(a)及历年插补MAE(b) |
由图 1b可以看出,1961—1964年最高、最低气温MAE明显比其他年份大,经查阅气象台站历史沿革原数据,蔡甸站1965年4月1日迁过1次站,新站距原站址3000m,海拔高度由27.7m提高到38.4m。经进一步分析,本次迁站导致了最高、最低气温序列不均一。根据3.1节,要插补1961—1964年的数据,须利用不连续年份1965年前后的数据建立回归模型估计插补值,这样就导致了1961—1964年MAE偏大。因此在进行资料插补时,尽量避开序列不连续的时间段。
3.3 极值误差最高、最低气温反映了气候冷暖变化程度,是判断极端气候事件强度的重要指标。在气候极值变化研究中多采用阈值进行分析,超过阈值的值被认为是极值,称该事件为极端事件。阈值分为绝对阈值和分位数阈值,绝对阈值即为一固定值(如最高气温≥38℃,最低气温≤-6℃),分位数阈值是动态的。潘晓华等[16]、DeGaetano等[17]利用最高、最低气温的分位数来研究极端气候事件和气候资料序列的均一性。为此有必要分析插补资料和观测资料所计算分位数的差异性。下面分别分析两种阈值的插补误差。
(1) 最高气温:选取最高气温观测值≥38.0℃与其对应插补值来分析当最高气温较高时的插补精度。1961—2006年共有24d最高气温观测值≥38.0℃,其中只有2d插补值大于观测值,其余22d均是观测值大于插补值,平均误差为0.57℃,MAE为0.63℃,远远大于最高气温MAE的(0.32℃),说明最高气温在出现极值时插补误差明显偏大,且插补值小于观测值(图 2a)。
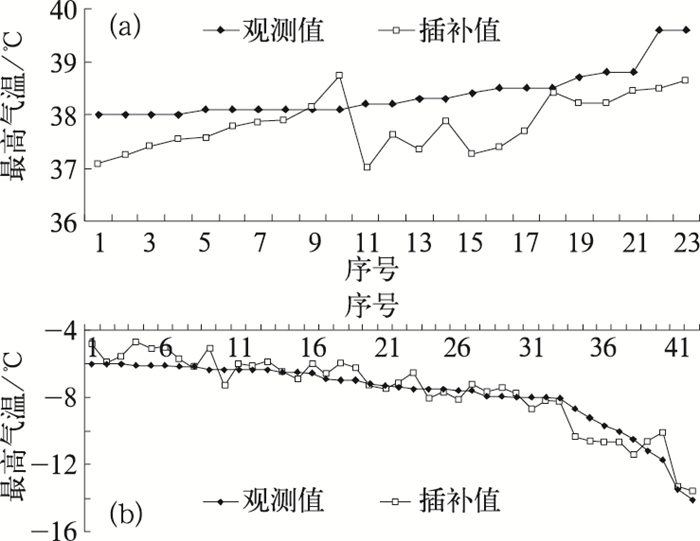
|
图 2 (a) 最高气温观测值≤38.0℃及其插补值;(b)最低气温观测值≤-6.0℃及其插补值 |
(2) 最低气温:选取最低气温观测值≤-6.0℃来分析最低气温较低时的插补精度。期间共有42d出现,其中25d观测值偏小,17d观测值偏大,平均误差为-0.17℃,其MAE为0.63℃,明显大于最低气温MAE的(0.45℃)(图 2b)。
(3) 分位数:利用1961—2006年共46年的逐日最高(低)气温的观测值和插补值,分别计算各月最高(低)气温的90%和95%(10%和5%)分位数。计算结果表明,最高气温90%、95%分位数观测值和插补值最大偏差分别为0.16和0.24℃,最低气温10%和5%分位数最大偏差分别为0.21和0.33℃。
3.4 绝对误差≥1.5℃分析由前面分析可知,日气温插补误差大部分(超过90%)在1.0℃以内,但还是有很少情况出现误差较大,为此探讨了在什么天气条件下误差绝对值较大(≥1.5℃),以便在今后工作中进一步提高插补精度。一般来说,日气温插补误差出现较大现象主要由插补站及其邻近站要素空间分布不均造成。产生原因主要有两个,一是天气系统的移动导致日气温变化规律不同步,二是局地天气系统导致气温剧烈变化。对于逐日气温而言,大幅降温、降水和风速是影响其变化规律的主要因子。为此本文分析了误差较大情况下的天气条件(表 6)。表中大幅降温事件的含义是:至少1站(插补站及其邻近站,下同)温度日较差≥14.5℃;风速事件含义是:至少1站风速≥4.5m·s-1,但无大幅降温事件发生;降水事件:至少1站降水量大于等于0.1mm,但无风速事件发生;无天气事件:上述天气事件均没发生。
|
|
表 6 绝对误差≥1.5℃的天气事件出现频率(%) |
由表 6可知,3个要素出现绝对误差≥1.5℃的天气事件频率都超过了60%,其中最高气温出现天气事件的频率达到88%,说明这些天气事件引起各要素时空分布不均,从而导致较大插补误差。
3.5 最大插补误差通过对蔡甸站1961—2006年46年插补误差计算,结果表明最高气温的最大正(负)误差为2.90℃(-2.50℃), 最低气温的最大正(负)误差为2.98℃(-2.57℃),平均气温的最大正(负)误差为2.60℃(-1.65℃),可见日气温最大绝对误差在3℃以内。
4 讨论本文虽然讨论的是连续数月缺测时的插补方法,但其方法同样适用于孤立的日气温缺测记录插补。在进行插补前,数据要经过质量控制。此外,被插补站的资料序列应连续,序列不均一性对插补误差精度影响较大。
由于LAD的解具有中位数性质[18],所以本文提出的方法对于气温处于极端值时插补误差有所增大,如对极值插补敏感,可采用文献[13]的方法进行修正。
本文提出的综合插补方法可以在实际业务中应用。后期主要工作是探讨日降水量插补方法。
| [1] |
Stooksbury DE, Idso CD, Hubbard KG. The Effects of Data Gaps on the Calculated Monthly Mean Maximum and Minimum Temperatures in the Continental United States: A Spatial and Temporal Study[J]. Journal of Climate, 1999, 12(5): 1524-1533. DOI:10.1175/1520-0442(1999)012<1524:TEODGO>2.0.CO;2 |
| [2] |
张永领, 丁裕国, 高全洲, 等. 一种基于SVD的迭代方法及其用于气候资料场的插补试验[J]. 大气科学, 2006, 30(3): 526-532. |
| [3] |
张秀芝, 孙安健. 利用车贝雪夫多项式进行资料缺测插补的研究[J]. 应用气象学报, 1996, 7(3): 344-352. |
| [4] |
张秀芝, 孙安健. 气候资料缺测插补方法的对比研究[J]. 气象学报, 1996, 54(5): 625-632. DOI:10.11676/qxxb1996.065 |
| [5] |
江志红, 丁裕国, 屠其璞.. 基于PC-CCA方法的气象场资料插补试验[J]. 南京气象学院学报, 1999, 22(2): 141-148. |
| [6] |
涂诗玉, 陈正洪. 武汉和宜昌缺测气温资料的插补方法[J]. 湖北气象, 2001, 3: 11-13. |
| [7] |
李军, 黄敬峰, 王秀珍, 等. 山区月平均气温的短序列订正方法研究[J]. 浙江大学学报(农业与生命科学版), 2005, 31(2): 165-170. |
| [8] |
Kemp WP, Burnell DG, Everson DO, Thomson AJ. Estimating missing daily maximum and minimum temperatures[J]. Journal of Climate and Applied Meteorology, 1983, 22: 1587-1593. DOI:10.1175/1520-0450(1983)022<1587:EMDMAM>2.0.CO;2 |
| [9] |
DeGaetano AT, Eggleston KL, Knapp WW. A method to estimate daily maximum and minimum temperature observations[J]. Journal of Applied Meteorology, 1995, 34: 371-380. DOI:10.1175/1520-0450-34.2.371 |
| [10] |
Reek T, Doty SR, Owen TW. A Deterministic Approach to the Validation of Historical Daily Temperature and Precipitation Data from the Cooperative Network[J]. Bulletin of the American Meteorological Society, 1992, 73(6): 753-762. DOI:10.1175/1520-0477(1992)073<0753:ADATTV>2.0.CO;2 |
| [11] |
Acock M.C, Pachepsky Y. Estimating missing weather data for agricultural simulations using group method of data handling[J]. Journal of Applied Meteorology, 2000, 37(4): 1176-1184. |
| [12] |
Huth R, Nemeová I. Estimation of Missing Daily Temperatures: Can a Weather Categorization Improve Its Accuracy?[J]. Journal of Climate, 1995, 8(7): 1901-1916. DOI:10.1175/1520-0442(1995)008<1901:EOMDTC>2.0.CO;2 |
| [13] |
Allen R.J, A.T DeGaetano. Estimating missing daily temperature extremes using an optimized regression approach[J]. Int. J. Climatol, 2001, 21: 1305-1319. DOI:10.1002/(ISSN)1097-0088 |
| [14] |
Eischeid J.K, P.A Pasteris, H.F Diaz, et al. Creating a Serially Complete, National Daily Time Series of Temperature and Precipitation for the Western United States[J]. J.Appl.Meteor, 2000, 39: 1580-1591. DOI:10.1175/1520-0450(2000)039<1580:CASCND>2.0.CO;2 |
| [15] |
李庆祥, MattheWJ.Menne, ClaudeN.Williams Jr, 等. 利用多模式对中国气温序列中不连续点的检测[J]. 气候与环境研究, 2005, 10(4): 736-742. |
| [16] |
潘晓华, 翟盘茂. 气温极端值的选取与分析[J]. 气象, 2002, 28(10): 28-31. |
| [17] |
DeGaetano A.T, R.J Allen, K.P Gallo. A Homogenized Historical Temperature Extreme Dataset for the United States[J]. J.Atmos.Oceanic Technol, 2002, 19: 1267-1284. DOI:10.1175/1520-0426(2002)019<1267:AHHTED>2.0.CO;2 |
| [18] |
张书毕, 高井祥, 高山. 最小绝对值和与最小二乘联合抗差估计[J]. 中国矿业大学学报, 1998, 27(1): 76-80. |
| [19] |
黄嘉佑. 气象统计分析与预报方法(第三版)[M]. 北京: 气象出版社, 2004: 20-23.
|
 2008, Vol. 34
2008, Vol. 34