2. 辽宁省丹东市气象台
2. Dandong meteorological Observatory, Liaoning Province
随着大气污染问题日趋严重,城市空气污染作为一个主要的环境问题正迅速凸现出来[1]。开展大气污染预报业务,为公众为政府决策提供有价值的参考信息,具有十分重要的意义。自2001年6月47个环保重点城市联合发布环境空气质量预报至今,相继有许多城市开展大气污染预报业务。随着气象业务技术体制改革的不断推进以及业务领域的不断拓展,大气污染预报越来越受到各级气象和环保部门的重视,并将其纳入常规预报业务。近20年来,大气污染预报模式的研究得到了很大的发展。中国气象科学研究院大气物理研究所徐大海、朱蓉[2]建立的城市空气污染数值预报系统(CAPPS),在对大气平流扩散方程积分基础上建立箱格预报模式,进行空气污染潜势预报;马雁军[3]、刘罡[4] 、王俭[5]、周秀杰[6]等将人工神经网络引入到大气污染预报,并取得较好效果。
近些年来,人工神经网络(Artificial Neural Network,ANN)技术得到较大发展,尤其是BP神经网络,广泛用于大气科学领域[7-11]。但在实际应用中发现,当输入样本较多且具有多重共线性时,会降低网络的训练速度和效率,影响预报精度。为此,本文引入主成分分析方法对样本进行预处理,以达到数据降维,去除相关性的目的。结合BP神经网络,将主成分作为输入层节点,以减少网络训练时间,提高网络训练精度,并将其应用于大气污染物浓度预报。
1 资料来源及处理研究所用SO2浓度数据由丹东市环境监测中心提供,包括城区4个环境空气质量自动监测站2005年、2006年采暖季(12月至次年3月)SO2浓度日均值。同步气象资料来源于丹东市气象台,包括气温、气压、风速等常规地面观测资料。用2005年的数据作为主成分分析和神经网络训练学习样本,建立神经网络模型,并采用2006年的数据进行预报验证。
计算4个空气自动站SO2浓度的平均值,以代表丹东城区日平均SO2浓度,将其作为预报量,将气温、气压、风速、相对湿度、蒸发等气象要素作为预报因子,进行相关分析,结果如表 1所示。
|
|
表 1 SO2浓度与气象因子相关系数 |
由表 1可知,除最小相对湿度、日照时数和平均气压,其余9个因子的相关系数检验显著水平均达到0.01。
2 SO2浓度预报模型的建立基于PCA-BP神经网络SO2浓度预报模型的建立,关键在于预报因子的主成分分析以及BP神经网络输入模型的确定和训练数据的选取。下面以丹东城区SO2日平均浓度预报为例,介绍预报模型的建立方法。
2.1 基于PCA的数据处理将表 1中相关系数检验显著水平达到0.01的预报因子构成9维随机向量X=(X1, X2, …, X9),应用SPSS统计软件对其进行主成分分析[12],得出特征值和其对应的特征向量(见表 2、表 3)。
|
|
表 2 方差分解主成分提取分析 |
|
|
表 3 特征值对应的特征向量(载荷) |
由表 2可以看出,前4个主成分的累积方差贡献比为91.795%>85%。据此,提取4个主成分,结合表 2的主成分系数构成如下4个主成分:
| $ \begin{align} &{{Z}_{1}}=0.26{{X}_{1}}+0.416{{X}_{2}}+0.399{{X}_{3}}+ \\ &\ \ \ \ \ \ \ 0.397{{X}_{4}}-0.090{{X}_{5}}-0.320{{X}_{6}}- \\ &\ \ \ \ \ \ \ 0.373{{X}_{7}}+0.401{{X}_{8}}-0.315{{X}_{9}} \\ \end{align} $ | (1) |
| $ \begin{align} &{{Z}_{2}}=-0.115{{X}_{1}}+0.366{{X}_{2}}0.356{{X}_{3}}+ \\ &\ \ \ \ \ \ \ 0.362{{X}_{4}}+0.471{{X}_{5}}+0.362{{X}_{6}}+ \\ &\ \ \ \ \ \ \ 0.318{{X}_{7}}-0.115{{X}_{8}}-0.358{{X}_{9}} \\ \end{align} $ | (2) |
| $ \begin{align} &{{Z}_{3}}=0.813{{X}_{1}}+0.036{{X}_{2}}-0.014{{X}_{3}}+ \\ &\ \ \ \ \ \ \ 0.091{{X}_{4}}-0.288{{X}_{5}}+0.276{{X}_{6}}+ \\ &\ \ \ \ \ \ \ 0.217{{X}_{7}}+0.314{{X}_{8}}+0.156{{X}_{9}} \\ \end{align} $ | (3) |
| $ \begin{align} &{{Z}_{4}}=-0.563{{X}_{1}}-0.011{{X}_{2}}-0.127{{X}_{3}}+ \\ &\ \ \ \ \ \ 0.075{{X}_{4}}-0.452{{X}_{5}}+0.322{{X}_{6}}+ \\ &\ \ \ \ \ \ 0.135{{X}_{7}}+0.542{{X}_{8}}+0.204{{X}_{9}} \\ \end{align} $ | (4) |
从主成分系数可以看出,平均气温、相对湿度在第一主成分上有较高载荷,第二主成分中蒸发量有较高的载荷,前日SO2浓度在第三和第四主成分上有较高的载荷。
2.2 PCA-BP神经网络模型的建立利用式(1)~(4)求得的4个主成分(Z1,Z2,Z3,Z4)作为BP神经网络输入层神经元矩阵,预报日SO2浓度标准化后(FSO2)作为其输出层神经元,利用MATLAB提供的神经网络工具箱[13](Neural Network Toolbox,简称NNbox)构建3层BP神经网络模型,如图 1所示。其中输入层为4个神经元,输出层为1个神经元。隐含层节点数的选择至今尚未找到一个很好的解析式,往往根据前人的经验和反复试验来确定。在相同总体误差情况下,选择收敛最快的;或用不同的隐层节点数训练网络,最佳隐层节点数由网络训练的最小系统误差确定出。
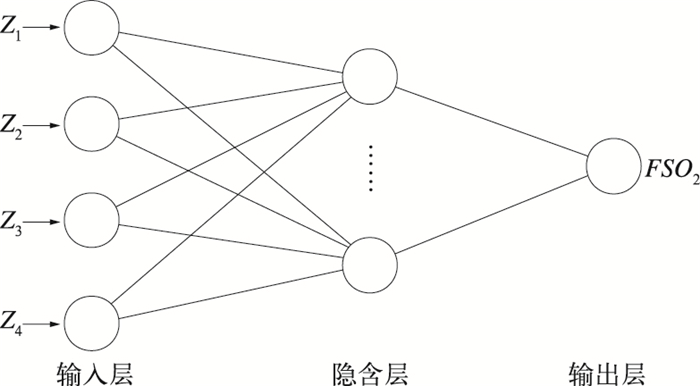
|
图 1 SO2浓度预报BP神经网络模型 |
将PCA处理后的2006年采暖季数据作为BP神经网络的训练样本,设隐层节点数初值为5,通过改变隐层节点数对网络进行训练,训练结果如表 4所示。
|
|
表 4 不同隐层节点数的BP神经网络训练结果 |
由表 4可以看出,当隐层节点数为10时,BP神经网络的系统误差最小,由此建立输入层为4个神经元,输出层为1个神经元,隐含层为10个神经元的BP神经网络,并利用该网络训练输出的隐含层权值w1和阈值b2及输出层权值w2和阈值b2,应用MATLAB的仿真函数simuff()建立采暖季SO2预报模型:
| $ \begin{align} &FS{{O}_{2}}=\text{simuff}(\mathit{P}, {{\mathit{w}}_{1}}, {{\mathit{b}}_{1}}, '\text{tansig}', \\ &\ \ \ \ \ \ \ \ \ \ \ \ {{\mathit{w}}_{2}}, {{\mathit{b}}_{2}}, '\text{Purelin}') \\ \end{align} $ | (5) |
其中:FSO2为预报日SO2浓度(标准化);P为主成分矩阵;tansig为正切S型传递函数;Purlin为线性传递函数。
利用式(5)对2005年采暖季SO2浓度进行拟合检验,并对2006年采暖季SO2浓度进行预报验证。
3 模型拟合及预报效果检验为了对比分析,建立了一般BP神经网络模型(数据未进行PCA处理)。利用2005年采暖季数据进行拟合检验。图 2为一般BP神经网络模型和PCA-BP神经网络模型SO2浓度拟合值与实际值的对比,经计算二者的拟合误差分别为0.005和0.002,拟合值与实际值相关系数分别为0.912和0.985。通过对比分析不难发现,基于PCA-BP神经网络模型比一般的BP神经网络模型拟合结果更为精确。由此可以说明,基于PCA-BP神经网络模型对SO2浓度具有良好的拟合能力。
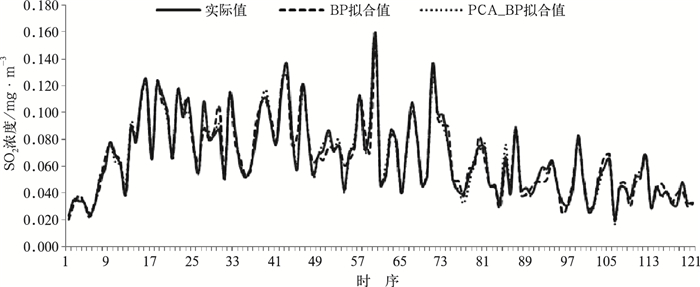
|
图 2 PCA-BP和BP神经网络模型SO2浓度拟合值与实际值对比 |
利用2006年采暖季数据进行预报验证,图 3为应用一般的BP神经网络模型和PCA-BP神经网络模型SO2浓度预报值与实际值对比,经计算二者的平均绝对误差为分别为0.0123和0.0098,预报值与实际值的相关系数分别为0.820和0.885。通过比较,可以看出,基于PCA-BP神经网络模型对采暖季SO2浓度具有良好的预报能力,其性能优于一般的BP神经网络模型,且预报结果更为准确。如果充分考虑影响采暖季SO2浓度的各种因子(如高空观测气象要素等),选择合理的隐层节点数,便能得到较好的预报效果。
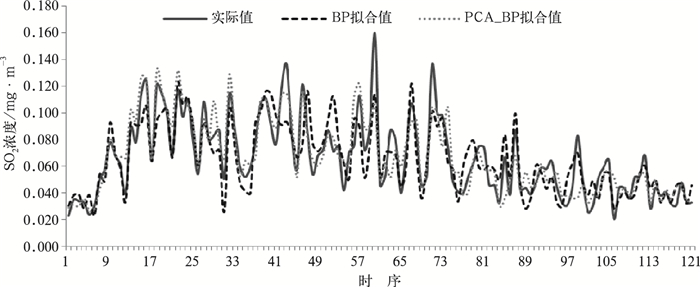
|
图 3 PCA-BP和BP神经网络模型SO2浓度预报值与实际值对比 |
(1) 将主成分分析引入BP神经网络的前处理,以原始预报因子的主成分作为网络的输入,降低了数据维数,消除了样本间存在的相关性,大大加快了BP神经网络的收敛速度,并且比一般的BP神经网络模型具有较高的拟合和预报精度。
(2) 将PCA-BP神经网络模型应用于丹东城区采暖季SO2浓度预报,预报值与实际值之间的绝对误差为0.0098,预报值与实际值的相关系数达到0.885。
(3) 应用2005年一个采暖季的资料建立PCA-BP神经网络模型,并对2006年采暖季SO2浓度进行预报试验,虽然得到了比较好的预报效果,但不排除偶然性的存在。随着观测资料的积累,将对模型做适当调整,以期建立更加稳健的预报模型。
(4) 鉴于PCA-BP神经网络模型对对采暖季SO2浓度具有良好的预报效果,可推广应用于其他大气污染物的浓度预报,但该方法是否适用,而且是否存在季节性的差异,能否应用于大气污染物浓度的逐时预报,还有待进一步研究,并将撰文详述。
| [1] |
张继娟, 魏世强. 我国城市大气污染现状与特点[J]. 四川环境, 2006, 25(3): 104. |
| [2] |
徐大海, 朱蓉. 大气平流扩散的箱格预报模式与污染潜势指数预报[J]. 应用气象学报, 2000, 11(1): 1-12. |
| [3] |
马雁军, 杨洪斌, 张云海. BP神经网络法在大气污染预报中的应用研究[J]. 气象, 2003, 29(7): 49. DOI:10.7519/j.issn.1000-0526.2003.07.011 |
| [4] |
刘罡, 李听, 胡非. 大气污染物浓度的神经网络预报[J]. 中国环境科学, 2000, 20(5): 429-431. |
| [5] |
王俭, 胡筱敏, 郑龙熙, 等. 基于BP模型的大气污染预报方法的研究[J]. 环境科学研究, 2002, 15(5): 62-64. |
| [6] |
周秀杰, 苏小红, 袁美英. 基于BP网络的空气污染指数预报研究[J]. 哈尔滨工业大学学报, 2004, 36(5): 582-585. |
| [7] |
张承福. 人工神经网络在天气预报中的应用研究[J]. 气象, 1994, 20(6): 43-47. DOI:10.7519/j.issn.1000-0526.1994.06.008 |
| [8] |
周曾奎, 韩桂荣, 朱定真, 等. 人工神经网络台风预报系统[J]. 气象, 1996, 22(1): 18-21. |
| [9] |
汤子东, 郑世芳, 奚秀芬. BP人工神经元网络在春季降水量预报中的应用[J]. 气象, 1997, 23(8): 34-37. DOI:10.7519/j.issn.1000-0526.1997.08.007 |
| [10] |
施丹平. 人工神经网络方法在降水量级中期预报中的应用[J]. 气象, 2001, 27(6): 40-45. DOI:10.7519/j.issn.1000-0526.2001.06.008 |
| [11] |
段婧, 苗春生. 人工神经网络在梅雨期短期降水分级预报中的应用[J]. 气象, 2005, 31(8): 31-36. DOI:10.7519/j.issn.1000-0526.2005.08.007 |
| [12] |
米红, 张文璋. 实用现代统计分析与SPSS应用[M]. 北京: 当代中国出版社, 2000.
|
| [13] |
丛爽编. 面向MATLAB工具箱的神经网络理论与应用(第2版)[M]. 北京: 中国科学技术大学出版社, 2003. 5.
|
 2008, Vol. 34
2008, Vol. 34