2. 宁波市气象台;
3. 兰州大学大气科学学院
2. Ningbo Meteorological Observatory;
3. Atmospheric Science College
提高数值预报模式时空分辨率有助于提高客观预报水平[1-2],但发展数值预报产品的解释应用技术也同样必要。目前数值预报的解释应用技术已在常规气象要素预报中取得了较好的效果[3],但是对于风速、降水等要素预报效果还不是十分理想。这一方面是由于风速、降水等要素本身非连续和非正态分布的特点所致,另一方面也由于导致这些天气现象的因素具有复杂多变和局域性强的特点。早在1990年代中期,范淦清[4]将风向风速进行预先处理,利用数值预报产品使用MOS方法制作江苏省各站点风的预报,为定点定量的风向风速预报作了很好的尝试。而后不少气象预报工作者用MOS[5]、神经元网络[6-7]等方法直接建立风向风速预报模型或分别建立U、V分量预报。
近年来有人应用相似方法来制作风预报。毛卫星等[8]用波谱分析相似法、邵明轩等[9]用K邻近域方法制作全国600多站点的风向风速预报,取得了较好的效果。最近,曾晓青等采用改进的KNN(K-nearest neighbor)方法[10]来解决降水这类非连续性气象要素的预报问题,该方法在搜索K邻近域的过程中,考虑天气事件出现的概率不同,分别求取有天气事件的正样本K+值和无天气事件的负样本K-值,使该方法选择的最邻近域中的K值取得更为合理。本文尝试将此方法应用到中国近海测站的日最大风速客观预报中。
1 资料与处理以我国近海测站日最大风速作为预报对象,用每天接收的ECMWF预报产品作为预报基本因子。所用资料来源于国家气象中心的MICAPS系统。
1.1 资料的分型处理不同风速是不同天气形势产生的结果。首先应用自组织神经网络方法进行天气分型分析[11]。参与分型的资料为2003年1月1日至2006年12月31日逐日ECMWF数值产品的分析场(12UTC),共计1389个有效样本。要素场包括海平面气压场、500hPa高度场、200hPa和850 hPa风场,分型范围:100~150°E、10~55°N。分型结果表明:11—3月的样本基本被分为同一类型。该类型平均环流形势基本特点是:500hPa东亚大槽槽底伸展到30°N附近,地面上则表现为25°N以北的中国大陆受到高压控制。这是我国冬半年的天气形势。自组织神经网络分析表明:冬半年影响我国的天气形势与其他季节不同,这一时段渤海、黄海、东海海域地面处于高压环流控制下,盛行偏北风,台湾海峡及以南海域盛行东北风。
1.2 预报对象的处理预报对象是测站日最大风速。通常日最大风速是不能实时得到的,以MICAPS资料中逐日8个时次地面观测风速的最大值代替。有必要对不同区域近海测站的逐日最大风速与常规8个时次地面观测风的最大值作一比较。表 1是2003—2006年11—3月共605天逐日8个时次地面观测风的最大值与实际逐日最大风速的差异。
|
|
表 1 11—3月日最大风速与8时次地面观测最大风速比较 |
表中可见:54区和58区11—3月地面观测逐日8时次风速的最大值平均比日最大风速小1.3m ·s-1左右,二者差值小于2.0m·s-1的天数达到75%,差值≥4.0m·s-1的天数仅占4%左右。而59区两者平均差异仅0.5m·s-1,且差值小于2.0m·s-1的天数达到98%,因此8时次地面观测风速的最大值可以近似地代表日最大风速。
这里预报对象都以逐日地面8个时次观测风速的最大值代表。将预报对象临界值分为18、15、12、10、8和6m·s-1共6个不同级别,并对每个级别的预报对象进行0、1化处理。共挑选了16个预报站点(表 2),其中54区和58区各5个测站,59区6个测站。
|
|
表 2 预报站点 |
以欧洲中心2004—2007年11—3月逐日数值预报产品作为基本因子资料,其中2004—20 06年资料用于建模,2007年1—3月资料用于预报检验。数值预报产品包括5层(海平面、850hPa、700hPa、500hPa、200hPa)8个时效(00、24、48、72、96、120、144、168小时)5个基本气象要素(温度、高度、纬向风、经向风、海平面气压)。利用这些基本气象要素通过动力诊断得出如涡度、散度、位温、垂直厚度以及一些物理量的平流、水平梯度等与风场相关的71个扩展物理量因子,用双线性插值方法将这些基本要素和扩充物理量插值到预报站点上,建成站点因子库。
建模时直接选取与测站日最大风速相关系数≥0.26的因子。如果因子总个数 < 10,则逐渐降低相关系数,以保证入选因子总数至少为10个。建模前对因子做了归一化处理。
2 KNN方法及参数的确定KNN(K-nearest neighbor)非参数估计技术[12-13]是近几年来在数值预报释用中发展较快的一种求解问题技术。在天气预报中,KNN方法集天气学预报思路和数值预报结果为一体,避开了建立预报方程需要作的种种假设。它基于历史样本建立模型,认为相似条件下发生的“行为"会产生相似的结果,因此对于风的预报是合理的。
KNN技术通过计算待预报数据样本X″j与历史数据样本中对应的每个子样本X′ij的距离,这里采用欧式距离作为相似判据:
| $ Dist{(X'', X{'_i})_j} = \sqrt {\sum\limits_{j = 1}^m {{{(X'{'_j}-X{'_{ij}})}^2}} } $ | (1) |
其中Di∈R, i=1, 2, ..., n;这样n个样本可得到n个距离。在所有距离中选择第k个最小的距离作为待预报数据的判断标准:
| $ DistK = {\rm{Min}}{\left( {Dist} \right)_k} $ | (2) |
通过统计训练样本中小于判别距离DistK的个数,把预测数据集的类别归到其中个数较多的一类中,从而做出预报。
KNN技术中的关键之一是K值的确定。在过去使用中,通常不考虑预报对象出现与不出现的样本数多寡,而是在所有的历史样本中寻找K个最优近邻。事实上,不同海域、不同等级的风速出现概率是很不相同的。考虑到样本数悬殊,本文应用KNN客观方法时,对历史样本中风速出现(为正样本)和不出现(为负样本)两种情况分别考虑,以确定各自的K 值,记为K+、K-。
| $ {K^ + } = \frac{{{N^-}}}{{{N^ + } + {N^-}}}K, {K^-} = \frac{{{N^ + }}}{{{N^ + } + {N^ - }}}K $ | (3) |
根据文献[10],K+、K-的选择是利用交叉验证方法。在参与建模的样本中,取一部分样本作为预报测试集,剩余部分作为训练集,对预报测试结果进行评估,通过不断的交叉更换预报测试样本,选择模型预测样本中的准确率和正样本的概括率都达到相对最优组合所对应的K+、K-作为最佳选择。
| $ \begin{array}{l} {\rm{Save}}{K^ + } = {K^ + }[{\rm{Min}}(\left( {1-{\rm{准确率}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1-正样品的概括率{\rm{ }}} \right))] \end{array} $ | (4) |
| $ \begin{array}{l} {\rm{Save}}{K^- } = {K^- }[{\rm{Min}}(\left( {1-{\rm{准确率}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1-正样品的概括率{\rm{ }}} \right))] \end{array} $ | (5) |
其中
| $ {\rm{准确率 = }}\frac{{{\rm{预报正确的样本}}}}{{{\rm{所有样本数}}}} $ | (6) |
| $ {\rm{正样本的概括率 = }}\frac{{{\rm{预报正确的正样本数}}}}{{{\rm{所有正样本数}}}} $ | (7) |
实际预报中,将某站点实时预报因子,依据上述确定的K+,K-值,从历史样本中选取最邻近域,K+和K-分别对应不同的距离(DistK+,DistK-),通过统计小于DistK+距离的正样本数和小于DistK-的负样本数,而后用预报判别值给出预报结论。
| $ \begin{array}{l} 预报判别值 = 小于Dist{K^ + }距离的样本数/\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;小于Dist{K^ + }距离的正样本数\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + {\rm{小于}}Dist{K^-}负样本数 \end{array} $ | (8) |
预报判别的阈值是通过历史资料的试预报,经比较判断给出。当计算出来的预报判别大于该给定阈值时,则认为有该类天气事件发生,反之则无。
上述KNN方法实现步骤见图 1。
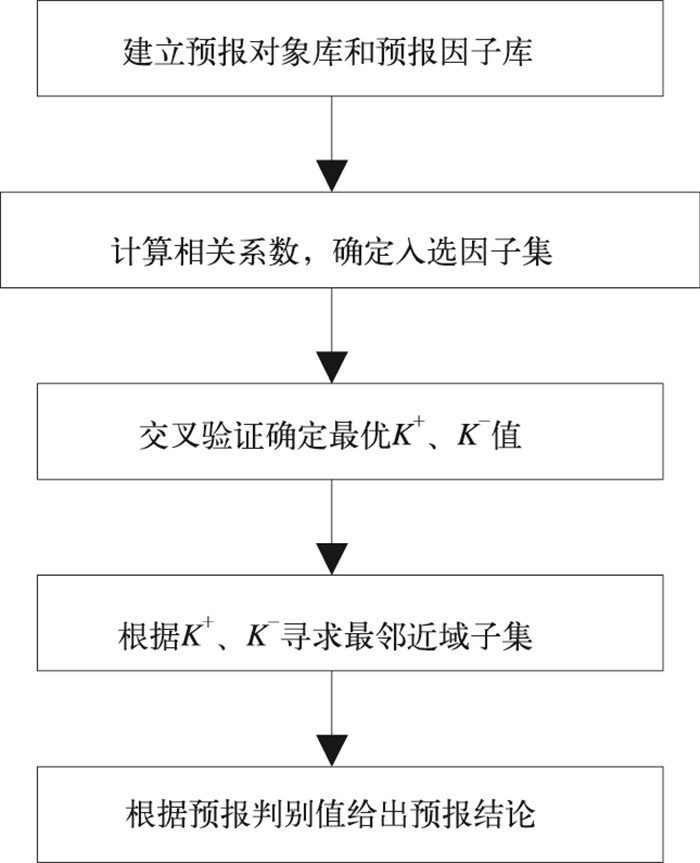
|
图 1 KNN方法实现流程 |
通过上述改进的KNN方法分别建立了11—3月中国16个近海测站不同预报时效的日最大风速预报模型,利用2007年1—3月ECMWF数值预报产品进行了逐日24~168小时不同风速级别、不同预报判别阈值下的预报检验,分别统计TS评分、空报率、漏报率和概括率。
3.1 区域预报评分结果表明当临界风速≥12m·s-1时,KNN方法所建模型仅对部分测站有预报能力,而临界风速≤10m·s-1时所建模型对各测站都有预报能力,因此区域TS评分分析仅针对≤10 m·s-1临界风速进行。
图 2为54区2007年1—3月逐日10、8、6m·s-1 3个不同临界风速24~168小时预报结果的TS评分、空报率和漏报率。分析发现:TS评分随着临界风速值的降低有整体提高的趋势,且不随预报时效的延长而下降。当临界风速为10m·s-1时,24~168小时的TS评分为0.3 ~0.428,当临界风速减小到6m·s-1时,TS评分提高到0.468~0.572。就空报率和漏报率分析,临界风速偏大时空报率相对较高,24~168小时预报基本在0.4以上,而漏报率一般在0.20左右,可见临界风速偏大时空报率是影响TS评分的主要原因。随着临界风速逐渐降低,漏报率对TS评分的影响逐渐增大,甚至可能超过空报率的影响。
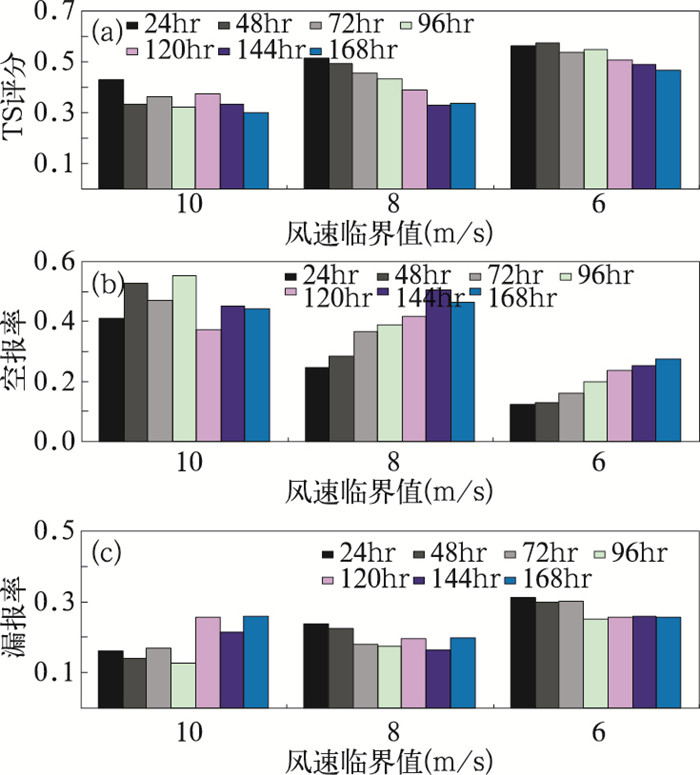
|
图 2 54区24~168小时预报TS评分(a)、空报率(b)、漏报率(c) |
与54区相比,58区TS评分与之持平,而59区的TS评分则略低于54区和58区。就空漏报率分析,当临界风速相对偏大时(8m·s-1以上),对于58区来说,空漏报率相当,在0.2~ 0.35之间,二者对TS评分几乎有相同的影响。随着临界风速值减小,空报率下降到0.1以下,漏报率仍维持在0.2~0.3之间,此时漏报率的影响大于空报率。而对于59区来说,空漏报率对TS评分的影响表现接近于54区。
可见3个区域的TS评分随临界风速的减小都是提高的。在不同临界风速时空漏报率对TS评分的影响是不同的。当临界风速相对大(10m·s-1)时,54区和59区空报率的影响大于漏报率,58区则二者相当,但临界风速较小(6m·s-1)时,3个区域的漏报率影响都大于空报率。
3个区域各测站TS评分分析还表明:无论在哪个风速等级,哪个预报时效,54776站表现都是54区是最好的,紧随其后的是54646和54751。而在58区各风速等级TS评分都大于区域平均值的是58472、58666和58974。59区相对表现好的测站有4个:59792、59559、59567和599 85。
按照浙江省业务评分标准,浙江沿海日最大风力从10.8m·s-1(6级)起评(表 3)。宁波市气象台沿海海面1—3月逐日最大风速24小时主观预报TS评分2007年和2006年分别为0.42和0.43,而58区所建模型2007年1—3月10m·s-1临界风速24小时预报TS评分为0.47。虽然评分标准和起评风速有差异,但还是表明模型有较好的客观预报能力。
|
|
表 3 浙江省海面风力质量评定标准 |
当临界风速为18m·s-1时,模型仅对4个站(54776、54646、58666、59567)具有预报能力。从24小时TS评分看,54776和54646站较另外2个站好,TS评分超过了0.4,而58 666和59567都在0.2以下。当临界风速从15m·s-1减小到12m·s-1时,各站TS评分总体趋势是提高的(图 3),其中54776和54646站的TS评分仍是较好的,24小时预报TS评分能达到0.5以上,58666站和59567站TS评分随着临界风速的减小而提高,由18m·s- 1时不足0.2提高到12m·s-1的0.5左右。
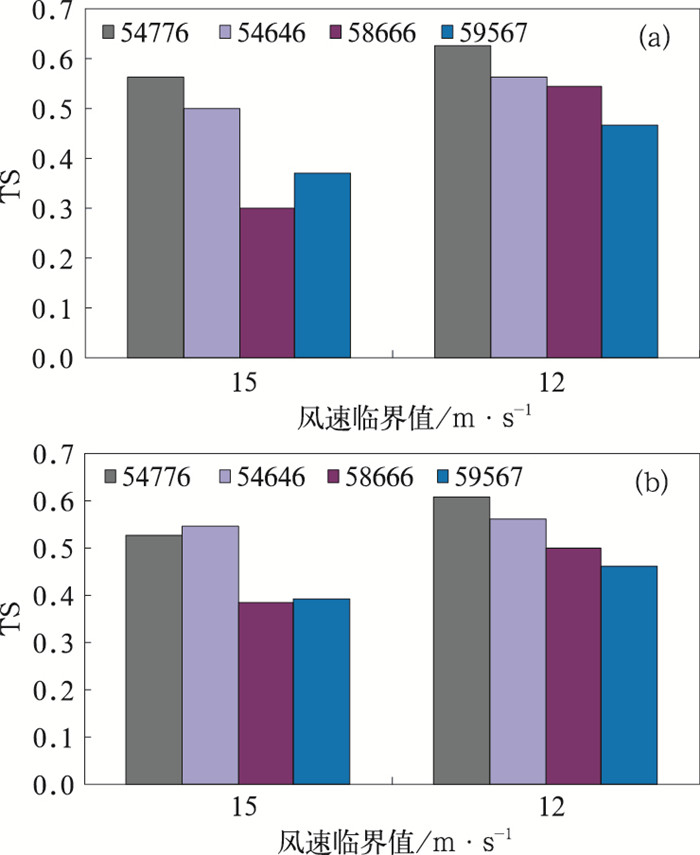
|
图 3 较大临界风速24小时(a)、48小时(b)预报TS评分 |
与区域TS评分有所不同的是,对于临界风速≥12m·s-1的站点,TS评分随预报时效延长是减小的。在24~72小时预报时效内,15m·s-1各站TS评分都在0.3~0.5,96小时降到0.25~0.35,120小时以后则都不到0.3,而12m·s-1各站24~96小时的TS评分变化不大,在0.4~0.6之间,120~168小时则降到0.3~0.5。
3.3 入选因子分析模型建立时是根据相关系数大小自动筛选因子。分析54区、58区和59区中TS评分相对好的3个测站(54776、58666、59792)24小时预报模型入选因子可以看出,3个站入选的相同因子有7个(地面气压的水平梯度、850hPa温度,x方向的地面气压水平梯度、850hPa V偏差风,850hPa经向风和850hPa风速),这些因子都与风直接相关。54776和58666站入选因子基本均匀分布在从地面到500hPa各个层次,而59792则集中在700hPa及其以下的中低层次,但3个站对日最大风速有影响的共同因子都集中在850hPa及以下层次。
从不同预报时效的入选因子看,3站24~96小时入选因子变化不大,只是随着预报时效的延长,相关系数大小逐渐降低,入选因子个数逐渐减少;在120~168小时预报时效时,入选因子差异才逐渐增大。表现出入选预报因子较好的稳定性。
对于各区域内TS评分相对差的测站(54579、58760、59981),分析发现其入选因子与TS评分较好的测站很不相同,表现在要么入选因子相关系数较低,要么入选因子及所在层次变化大,且入选因子随预报时效的变化明显,表现出预报因子的不确定性很大。
3.4 预报判别阈值讨论预报判别阈值可以进一步控制预报样本与历史样本相似程度,其大小的选定应针对不同测站在不同的临界风速下选定不同的值。预报试验中,分别选取从0.5~0.8之间每间隔0.05的预报判别阈值在不同测站不同预报时效时的TS评分,发现不同临界风速时要使TS评分达到最大,则相应的预报判别阈值设定是有所不同的。如54776站,当临界风速为18m·s-1时,试报结果表明预报判别阈值≥0.70时TS评分能达到较好的值,而对于15m·s-1的临界风速,则最小预报判别阈值至少设定在0.60。总之,针对不同测站不同等级的风速预报,其预报判别阈值应当有所不同。分析发现:如果设定的临界风速对于测站来说发生概率相对小,则可以适当提高预报判别阈值,以减少空报率,提高TS评分。
4 结论与讨论本文将KNN技术应用到近海测站日最大风速预报时,对不同测站、不同风速等级、不同判别阈值进行了试报。结果表明:
(1) 不同海区入选因子层次分布是不同的,但预报效果较好的站点所选因子基本符合预报员对产生风速影响因素的认识,这些关系应当是稳定的。而预报效果较差的站点,入选因子就比较乱,可以认为他们的关系不够稳定,还有待积累更多的样本资料给予进一步考察。
(2) 临界风速≤10m·s-1的区域预报效果分析表明:3个区域TS评分随着临界风速的减小有升高趋势,但TS评分随预报时效变化不大。当临界风速相对大(10m·s-1)时,54区和59区空报率的影响大于漏报率,58区则二者相当,随着临界风速减小到6m·s-1时,3个区域的漏报率影响都大于空报率。与主观预报TS评分相比,模型表现出较好的客观预报能力。
(3) 临界风速≥12m·s-1时模型仅对部分站点有预报能力,站点TS评分随着预报时效的增加是减小的。
(4) 无论临界风速等级大小,模型对54776、54646、58666和59567的预报效果始终是各区域最好的,可以作为日常预报中多加参考的测站。
(5) 当风速预报等级对于测站相对发生概率较小,可以适当预报判别阈值,以控制空报率,提高TS评分。
(6) 11—3月影响我国的天气形势类型相似,因此预报对象为近海测站日最大风速,没有考虑风向的问题。
本文所建预报模型还有待完善。如建模时资料还不是足够长(ECMWF数值产品中的流场资料从2004年10月1日开始才比较全面),因子筛选完全根据相关系数大小自动筛选,入选因子可能并不相互独立。随着资料长度的累加,在今后的改进工作中,有必要进一步加强研究和试验,使筛选的因子更加合理完善,提高KNN方法的预报效果。
| [1] |
张建海, 王国强. 客观预报中多时刻因子的应用及其效果[J]. 气象, 2005, 31(5): 62-65. DOI:10.7519/j.issn.1000-0526.2005.05.014 |
| [2] |
龚强, 袁国恩, 汪宏宇, 等. 应用MM5模式对地面风速过程的模拟试验[J]. 气象, 2005, 31(4): 53-57. DOI:10.7519/j.issn.1000-0526.2005.04.012 |
| [3] |
刘还珠, 赵声蓉, 赵翠光, 等. 国家气象中心气象要素的客观预报——MOS系统[J]. 应用气象学报, 2004, 4, 15(2): 181-191. |
| [4] |
范淦清. 风预报的数值产品释用研究[J]. 气象, 1995, 21(10): 47-50. DOI:10.7519/j.issn.1000-0526.1995.10.012 |
| [5] |
林良勋, 程正泉, 张兵, 等. 完全预报方法在广东冬半年海面强风业务预报中的应用[J]. 应用气象学报, 2004, 5(4): 485-490. |
| [6] |
胡波, 杜惠良. 浙江省沿海海面日极大风预报[J]. 海洋预报, 2006, 23(B09): 64-67. |
| [7] |
杨忠恩, 陈淑琴, 黄辉. 舟山群岛冬半年灾害性大风的成因与预报[J]. 应用气象学报, 2007, 18(1): 80-85. DOI:10.11898/1001-7313.20070114 |
| [8] |
毛卫星, 许晨海, 何立富, 等. 多时次多尺度波谱相似预报风要素[J]. 气象, 2005, 31(10): 28-31. DOI:10.7519/j.issn.1000-0526.2005.10.007 |
| [9] |
邵明轩, 刘还珠, 窦以文. 用非参数估计技术预报风的研究[J]. 应用气象学报, 2006, 17(增刊): 125-129. |
| [10] |
曾晓青, 邵明轩, 刘还珠, 等. 基于交叉验证技术的KNN方法在降水预报中的试验[J]. 应用气象学报, 待发表. http://cn.bing.com/academic/profile?id=17a1e175d15fd13dfd19f9b8ad8eb0a3&encoded=0&v=paper_preview&mkt=zh-cn
|
| [11] |
黄卓, 杨洪敏, 郝为, 等. 基于智能聚类的综合相似预报[A]. 暴雨落区预报实用方法[C]. 北京: 气象出版社, 2000: 53-59.
|
| [12] |
翟宇梅, 赵瑞星. 概率天气预报的K近邻非参数估计仿真模型[J]. 系统仿真学报, 2005, 17(4): 786-788. |
| [13] |
翟宇梅, 赵瑞星, 肖仁春, 等. K近邻非参数回归概率预报技术及其应用[J]. 应用气象学报, 2005, 16(4): 453-460. DOI:10.11898/1001-7313.20050405 |
 2008, Vol. 34
2008, Vol. 34