2. 南京大学大气科学系
近年来, 热带气旋登陆(Landfall)问题的研究倍受重视。热带气旋大灾都是在其登陆前后造成的。陈联寿等[1]指出, 登陆台风因地形或环境辐合作用, 常在其外围形成中尺度涡旋, 当这种涡旋与台风相互作用被吸入内核区时, 台风涡量将增加, 有利于台风在陆上维持。姚才等[2]分析了华南登陆台风榴莲的能量变化,揭示了登陆台风衰减过程中的能量演变特征。陈受钧等[3]用一个低通滤波器, 成功分离出天气尺度与次天气尺度系统, 研究了暴雨系统中两类运动之间的动能转换, 认为次天气系统在动能平衡中起重要作用。寿绍文等[4]、胡坚[5]、万齐林[6]分别从两种尺度相互作用出发, 分析了台风与其外围暴雨之间的能量转换。李英等[7]采用移动坐标以及云顶亮温(TBB)和常规资料, 对热带气旋在陆上维持期间的次天气尺度环流特征及其与次天气尺度系统之间的相互作用进行对比分析和诊断。
值得注意的是,采用数值模拟的方法来分析考虑地形的影响下,登陆热带气旋环流中天气尺度与次天气尺度系统相互作用对其陆上维持影响的研究还较少。本文拟选取登陆台风麦莎(2005)为研究对象,通过中尺度模式进行数值模拟,在考察模拟效果较好的基础上,采用一个低通滤波器,分离登陆热带气旋环流中天气尺度和次天气尺度系统,深入分析泰山地形对两种尺度动能和涡度转换的影响。
文中所使用的模式是美国宾州大学和美国国家大气科学研究中心的非静力平衡中尺度模式MM 5(V3)。模拟区域4.3°S~71.3°N、84.9~149.7°E,双重嵌套网格格距分别为60和20km。垂直方向为不等距的23层。以6小时间隔,1°×1°的NCEP再分析场为模式提供初始场和侧边界条件。采用时变侧边界条件,初始时刻为2005年8月7日00时(UTC),积分进行48小时,每3小时输出一次结果。全文中时次均采用世界时。模式的物理过程主要包括:B lackadar高分辨的边界层参数化方案,粗网格Kuo积云参数化方案,细网格Grell积云参数化方案,混合相显式水汽方案。
1 模拟效果检验台风麦莎(2005)登陆后沿西北行进后转为北行, 途经多省, 强度减弱,于8月7日前后开始影响山东, 此时泰山位于热带气旋环流区域内, 本文即选取该小地形为研究对象, 深入分析其对热带气旋结构及热带气旋环流中天气尺度和次天气尺度系统动能和涡度转换的影响。
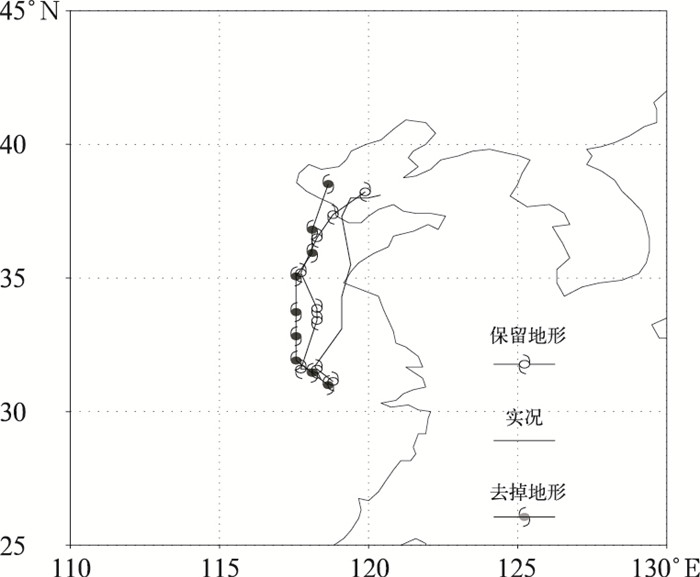
图 1为热带气旋麦莎于2005年8月7日00时(UTC)到8月9日00时(UTC)的陆上移动路径,图中包含的三条路径分别为保留了泰山地形、去掉了泰山地形及实况。从图中可以看出,保留地形的数值模拟较好的再现了麦莎台风登陆后期的陆上移动路径,虽然与实况相比仍有一定差距,但对于热带气旋走势把握比较好,尤其是临近出海地点与实况很吻合,同时发现泰山地形对路径的模拟没有起到决定性作用,只是在热带气旋再次入海的地点模拟上存在差异。总的来说,此次模拟是比较成功的,基于此,下面将进一步研究地形对台风麦莎的影响。
|
图 1 麦莎台风6h一次的移动路径 |
本文将采用文献[7]中提到的方法,跟踪考察登陆过程中热带气旋的次天气尺度环流特征。即以各时刻热带气旋中心所在位置作为坐标原点, 选取一定区域进行研究。拟进行两组实验:(1)控制实验(保留泰山地形);(2)敏感性试验(去掉泰山地形)。分别考察两个实验中热带气旋环流中天气尺度与次天气尺度的相互作用,以期得到较有意义的结论。
2.1 滤波方法对任一物理量F, 可写为
| $ F = {F^*} + F' $ | (1) |
F*为F的天气尺度部分, F′为次天气尺度部分。
夏大庆等[8]分析研究了气象场的几种中尺度分离算子,通过理论分析和个例计算,认为25点滤波算子(S1=0.5, S2=0.667)在中尺度分离中效果最佳。本文即选取该方法对常规物理量场进行1次平滑, 提取波长约为400km的次天气尺度系统F′。热带气旋尺度约为1000~1500km, 为天气尺度系统。
| $ \begin{array}{l} \overline {{f_0}} = {\left[{\left( {1-{S_1}} \right)\left( {1-{S_2}} \right) + \frac{{{S_1}{S_2}}}{2}} \right]^2}{f_0} + \\ \;\;\;\;\;\frac{1}{2}[{S_1}(1-{S_2}) + {S_2}(1-{S_1})]\\ \;\;\;\;\;[(1-{S_1})(1-{S_2}) + \frac{{{S_1}{S_2}}}{2}]\sum\limits_{i = 1}^4 {{f_i}} + \\ \;\;\;\;\;\frac{1}{4}{[{S_1}(1-{S_2}) + {S_2}(1-{S_1})]^2}\sum\limits_{i = 5}^8 {{f_i}} + \\ \;\;\;\;\;\frac{{{S_1}{S_2}}}{4}[(1-{S_1})(1-{S_2}) + \frac{{{S_1}{S_2}}}{2}]\sum\limits_{i = 9}^{12} {{f_i}} + \\ \;\;\;\;\;\frac{{{S_1}{S_2}}}{8}[{S_1}(1-{S_2}) + {S_2}(1-{S_1})]\sum\limits_{i = 13}^{20} {{f_i}} + \\ \;\;\;\;\;\;{(\frac{{{S_1}{S_2}}}{4})^2}\sum\limits_{i = 21}^{24} {{f_i}} \end{array} $ | (2) |
动能方程中天气尺度和次天气尺度系统转换项V*·I*的水平运动项和垂直运动项分别为(具体公式推导见文献[9]):
| $ \begin{array}{l} {({V^*}\cdot{I^*})_H} =- {u^*}[\frac{\partial }{{\partial x}}({\left( {uu} \right)^*}-{\rm{ }}{u^*}{u^*}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{\partial }{{\partial y}}({\left( {uv} \right)^*}-{u^*}{v^*})] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{v^*}[\frac{\partial }{{\partial x}}({\left( {uv} \right)^*}-{u^*}{v^*}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{\partial }{{\partial y}}({\left( {vv} \right)^*}-{v^*}{v^*})] \end{array} $ | (3) |
| $ \begin{array}{l} {({V^*}\cdot{I^*})_V} =-{u^*}\frac{\partial }{{\partial p}}({\left( {\omega u} \right)^*}-{\omega ^*}{u^*})\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;-{v^*}\frac{\partial }{{\partial p}}({\left( {\omega v} \right)^*} - {\omega ^*}{v^*}) \end{array} $ | (4) |
V*·I*正值表示次天气尺度运动向天气尺度系统提供动能, 负值表示次天气尺度系统从天气系统获得动能。
垂直涡度方程中天气尺度和次天气尺度系统转换项Iζ的水平运动项和垂直运动项分别为:
| $ \begin{array}{l} I_\zeta ^H =-\frac{\partial }{{\partial x}}({\left( {\zeta u} \right)^*}-{\zeta ^*}{u^*})-\\ \;\;\;\;\;\;\;\;\frac{\partial }{{\partial y}}({\left( {\zeta u} \right)^*} - {\zeta ^*}{u^*}) - \\ \;\;\;\;\;\;\;\;\frac{\partial }{{\partial x}}({\left( {\zeta v} \right)^*} - {\zeta ^*}{v^*}) - \\ \;\;\;\;\;\;\;\;\frac{\partial }{{\partial y}}({\left( {\zeta v} \right)^*} - {\zeta ^*}{v^*}) \end{array} $ | (5) |
| $ I_\zeta ^V =-\frac{\partial }{{\partial p}}({\left( {\zeta \omega } \right)^*}-{\zeta ^*}{\omega ^*}) $ | (6) |
Iζ>0,表示两种尺度相互作用的结果是次天气尺度系统给天气尺度系统提供正涡度;Iζ<0,表示天气尺度系统给次天气尺度系统提供正涡度。
取热带气旋为中心的(15°×15°)经纬度范围为热带气旋区域, 用式(3)和(4)计算区域平均动能转换项[V*·I*]([]表示取区域平均), 式(5)和(6)计算区域平均涡度转换[Iζ]。再分别求1000~700hPa, 600~400hPa和300~100hPa层的平均值, 代表低层、中层和高层的转换。
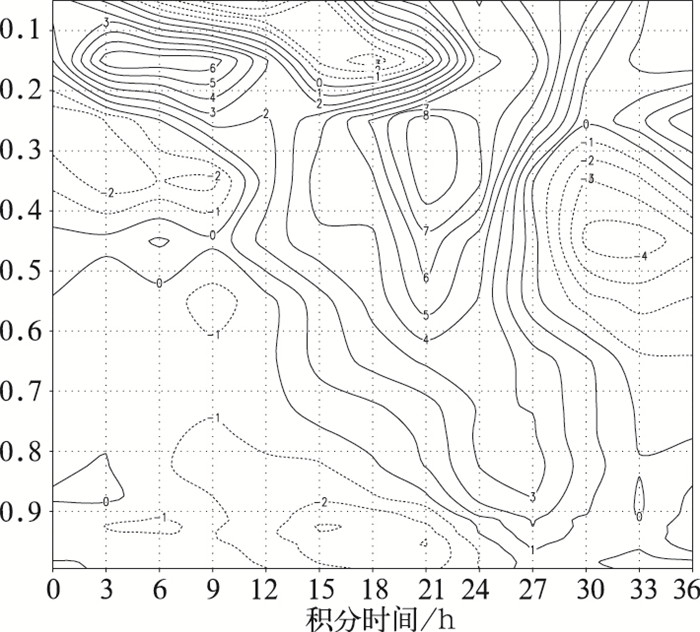
3 结果分析 3.1 对流层涡旋结构将两组敏感性试验模拟结果相减求差值,并对泰山地形区求取面积平均,深入分析模拟热带气旋麦莎北上深入内陆的过程中,泰山地形对其涡旋性的影响。图 2为泰山地形区平均涡度差值场时变图。从图中可以看出,随着积分时间的增长,模拟热带气旋中心逐渐北上移近泰山地形区,该区上空对流层中高层正涡度不断增强,于积分24小时达到最大值,中心值为8×10-5s-1。这表明保留泰山地形的情况下,热带气旋涡旋性明显强于去掉地形的情况,且这种影响随气旋中心与地形间距离的缩小而逐渐增强。
|
图 2 泰山地形区平均涡度差值场时变图 单位:10-5s-1 |
为了更清晰地看出泰山地形对热带气旋环流的影响,我们采用同样的方法求得积分各时刻两组试验的流场差值,图 3为积分24小时对流层不同层次的流场差值分布。在图 3a中,对流层低层泰山地形区存在明显的气流辐合,其东侧已形成一个明显的气旋性旋涡,而在对流层高层(图 3b),泰山地形区上空已形成较强的气旋性涡旋,该结果进一步证明了保留泰山地形对维持热带气旋气旋性强度的正贡献,且这种正贡献在对流层中高层表现得更明显。

|
图 3 积分24小时流场差值图 (a) σ=0.925,(b) σ=0.55 |
表 1中所列为保留地形的情况下热带气旋麦莎与次天气尺度之间动能转换项的值。由表 1可见,[V*·I*]V比[V*·I*]H大一个量级,最大的转换均出现在高层。
|
|
表 1 保留地形时麦莎区域平均动能转换项的时间演变(10-5W/(kg·m2)) |
整个积分时段内,[V*·I*]H在低层和高层基本为正值,中层[V*·I*]H有5个时次出现负值,但与同时次的低层、高层的正值相比为小项。而[V*·I *]V的情况则不同,整个积分时段内中层[V*·I*]V均为负值,高层也出现了几次负值,与[V*·I*]H分布相似的是,低层[V*·I*]V基本为正值。两项的综合作用[V*·I*]的结果显示,低层[V*·I*]基本为正值,中层[V*·I*]为负值,高层正负值交替出现。这说明高、低层,尤其是低层,热带气旋麦莎从次天气尺度系统中获得了动能,虽然在中层热带气旋动能被次天气尺度系统所消耗,但这部分动能从高、低层得到了补充,因此,从整体上来说,麦莎获得了次天气尺度系统的动能,有利于它的维持。
表 2为去掉地形的情况下热带气旋麦莎与次天气尺度之间动能转换项的值。可以看出,[V*·I*]V比[V*·I*]H基本为同一个量级,与保留地形相比[V* ·I*]V的作用明显减小,其分布也发生了较大的变化。低层[V*·I*]H仍然为正值。去掉地形后,高层[V*·I*]V全部变为负值,而中层[V*·I*]V则变为正值或弱的负值,低层[V*·I*]V在积分24小时转为负,并持续了至少6个小时。热带气旋的两项的综合作用[V*·I*]显示,高层为负值或弱的正值,中低层基本为正值,但与表 1相比,低层[V*·I*]明显变小,这说明在低层次天气尺度系统向热带气旋输送的动能变少,再加上高层热带气旋向次天气尺度系统的动能输送,整层[V*·I*]的正值明显减少。积分24小时地形对热带气旋影响最直接,对比两表的整层[V*·I*]可以发现,保留地形的情况下[V*·I*] 的值大于0且大于去掉地形的情况。这说明热带气旋从次天气尺度系统获得动能,实验证明这主要是由地形所引起的。通过对比可以看出,有无地形可以对两种尺度间动能交换产生较明显的影响,去掉地形后,热带气旋从次天天尺度系统那里得到的动能减少,这势必影响到热带气旋强度的变化。
|
|
表 2 去掉地形时麦莎区域平均动能转换项的时间演变(10-5 W/(kg·m2)) |
表 3显示保留地形的情况下热带气旋麦莎与次天气尺度之间涡度转换项的值。与动能转换不同的是,[IζH]与[IζV]属于同一量级。最大的涡度交换仍然出现在高层。低层[IζH]主要为负值,中层[IζH]在积分中后期由正转为负,高层[IζH]除积分中期为正外均为负值。[IζV]在对流层各层的分布从总体上看与[IζH]很相似。两项的综合作用[Iζ]显示,低层与高层[Iζ]在涡度转换中基本起着相反的作用。中层[Iζ]主要为正值。整层[Iζ]在积分中期为正,其余时间为正负交替出现。可以看出,积分中期热带气旋从次天气尺度系统获得正涡度,而这段时间正是麦莎受小地形影响的主要时期。
|
|
表 3 保留地形时麦莎区域平均涡度转换项的时间演变(单位:10-9 s-2/m2) |
去掉地形后可以看到,低层[IζH]全部变为负值,中层变化不大,高层[IζH]与保留地形时相比作用相反。去掉地形后,低层[IζV]符号没有发生变化,但值得注意的是,当低层[IζV]为负即热带气旋失去正涡度时,其绝对值大于保留地形时的低层[IζV],这说明在受地形影响最大的低层热带气旋向次天气尺度系统输送正涡度的程度加大了。两项的综合作用[Iζ]更加说明了这一点,整层[Iζ]积分12小时后基本转为负值,尤其是8月8日00时(积分24小时)前后12小时内,已经由保留地形时的正值变为负值。与表 3对比可以看出,热带气旋不仅没有从次天气尺度系统获得正涡度,反而将自身的正涡度向外输送,这更加说明地形对登陆热带气旋的影响不可忽略。
|
|
表 4 去掉地形时麦莎区域平均涡度转换项的时间演变(单位:10-9s-2/m2) |
本文选取2005年第9号台风麦莎为研究个例,采用MM5中尺度模式模拟再现了麦莎登陆后北上深入内陆的演变过程,通过敏感性试验对比与尺度间动能和涡度转换的分析,讨论地形对热带气旋涡旋性强度的影响以及造成这种影响的物理机制。结论如下:
(1) 地形的存在有利于维持热带气旋涡旋性强度,这种影响随气旋中心与地形间距离的缩小而逐渐增强,且这种强度的增强在对流层中高层表现得更为明显。
(2) 地形对两种尺度间动能转换的影响主要表现为:保留地形的情况下,热带气旋主要在对流层低层获得次天气尺度系统动能,当去掉地形后,垂直运动的贡献减小;对低层转换项影响比较大,低层次天气尺度系统向热带气旋输送的动能变少;高层转换项也受到影响,次天气尺度系统对热带气旋动能的消耗增大。
(3) 地形对两种尺度间涡度转换的影响主要表现为:保留地形时热带气旋总体上是从次天气尺度系统中获得正涡度;当低层涡度转换项的垂直运动贡献为负时,去掉地形会加剧这种负贡献,即次天气尺度系统从热带气旋得到更多的正涡度;从整体上看,去掉地形后,热带气旋不仅没有从次天气尺度系统获得正涡度,反而将自身的正涡度向外输送。
| [1] |
陈联寿, 徐祥德, 罗哲贤, 等. 热带气旋动力学引论[M]. 北京: 气象出版社, 2002: 317.
|
| [2] |
姚才, 张诚忠, 黄明策. 华南登陆台风"榴莲"的能量分析[J]. 气象, 2001, 30(6): 12-17. |
| [3] |
陈受钧, 谢安. 次天气尺度与天气尺度系统之间动能交换的诊断分析[J]. 气象学报, 1981, 39(4): 408-415. DOI:10.11676/qxxb1981.044 |
| [4] |
寿绍文, 励申申, 王信. 登陆台风动能平衡和转换特征[J]. 南京气象学院学报, 1994, 17(1): 27-31. |
| [5] |
胡坚. 华东地区台风暴雨的诊断研究[J]. 大气科学, 1991, 15(3): 111-117. |
| [6] |
万齐林. 热带气旋外围环流中次天气系统与天气尺度系统相互作用的诊断分析[J]. 热带气象, 1991, 7(4): 372-377. |
| [7] |
李英, 陈联寿, 徐祥德. 登陆热带气旋维持的次天气尺度环流特征[J]. 气象学报, 2004, 62(3): 257-267. DOI:10.11676/qxxb2004.027 |
| [8] |
夏大庆, 郑良杰, 董双林, 等. 气象场的几种中尺度分离算子及其比较[J]. 大气科学, 1983, 7(3): 303-311. |
| [9] |
丁一汇. 天气动力学中的诊断分析方法[M]. 北京: 科学出版社, 1989: 83.
|
 2008, Vol. 34
2008, Vol. 34