2. 中国气象局北京城市气象研究所
2. The Institute of Urban Meteorology, CMA
气象服务随着国民经济的发展而逐步深入到各个行业,气象条件成为影响部分企业经营的重要自然因素之一。企业可利用气象服务信息来完善其经营方式,甚至参与一些重大经营决策。气象服务能否真正融入企业经营决策并产生效益,需要从理论上解决两个关键问题:一是考虑到天气因素对企业经营有重大影响,但对未来天气或气候变化情况无法把握,这时如何决策;二是认为现有的气象服务信息可信,如何利用这类信息来参与企业决策以获取最大期望效益。这两个问题是普遍存在的,前者需要解决的是随机决策下的不确定判定,后者的随机决策可“铆定”在决策树模型的基础上[1],做出最大期望估算。随机决策模型在地理[2]、金融[3]、管理[4]、计算机系统工程[5-6]等领域的应用十分广泛。由于随机决策问题中的自然状态概率体现为未来某类天气或气候状况的出现几率,随机决策方法很适用于气象服务领域,目前国内还鲜有此类工作可供借鉴。本文首先对随机决策模型的概念加以阐述,随后采用案例,分析了随机决策方法在气象服务领域中的应用、实施步骤及方法,力图从原理层面及实际应用方法上展现模型的实用性、可行性等特征。应用结果表明随机决策方法为指导企业用户更好应用气象服务信息,改进企业经营具有较高利用价值,为拓宽气象服务需求及扩大气象服务的社会影响及效益提供理论及方法论基础。
1 随机决策问题的基本概念定义1(决策问题):对于一个需要处理的事件,面临几种客观条件,又有几种可供选择的解决方案,这就构成了一个决策问题。案例1即为气象服务中的一个典型决策问题。
定义2(自然状态):决策者所面临的每一种客观条件称之为一种自然状态,并不以人的主观意志为转移。案例1中,未来出现冷冬或出现暖冬即为两种自然状态。
定义3(行动方案):决策问题中,那些可供选择的方案称为行动方案。案例1中的经营方案d1、d2和d3为三种行动方案。
定义4(状态概率):决策问题中,每一种自然状态出现的概率称为状态概率。在案例1中冷冬出现的概率即为状态概率。状态概率预测的准确与否,是风险决策的关键点之一。气象服务中的风险决策需建立在天气预报或气候预测基础之上。
定义5(益损值):每一种行动方案在各种自然状态下所获得的收益或者损失称为益损值。在气象服务中,专业气象台应与服务对象进行良好的沟通,尽量准确的估算出各种自然状态下的益损。
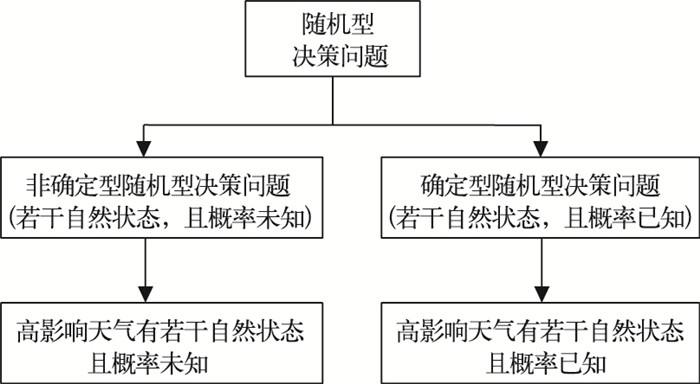
根据自然状态的概率是否可知,将气象服务中的随机决策问题分为两类,如图 1所示。
|
图 1 气象服务中随机型决策问题的分类 |
当自然状态的概率无法得知时,常用不确定性决策方法。在气象部门对于未来高影响天气出现的概率把握不大时,可根据服务对象的经营风格或者对待风险的偏好,采用不确定性决策方法进行服务决策。下面用案例1,说明不确定型决策模型的方法原理及使用步骤。
案例1:某皮靴生产厂家在本地专业气象台的协助下制定未来冬季的生产经营策略。若气象部门预测为暖冬,则生产厂家会减少皮靴的生产规模,采取保守型经营策略d1;若为平常的冬季,则会采取适中的生产规模,采取稳健型经营策略d2。若预测为冷冬,则会扩大毛皮靴的生产规模,采取冒险型经营策略d3。问假如专业气象台对未来出现冷冬的概率把握性不大时,应推荐厂家采取何种策略?
步骤1:与生产厂家一起,确定各方案在不同自然状态下的益损值
专业气象台首先确定两种可能出现的自然状态:未来出现冷冬(记为S1)和未来不出现冷冬(记为S2),并与生产厂家一起估算。假定两种自然状态下预期的益损值如表 1所示。
|
|
表 1 三个备选经营方案的预期益损值(单位:万元) |
用矩阵形式所表示的各方案在不同自然状态下最终收益或损失结果的集合,称为益损矩阵[7]。显然,益损矩阵需要气象部门和生产经营部门相互协作获得。案例1可按照如下方法进行:(1)皮靴生产厂家首先根据自己的生产能力,分别计算保守型、稳健型和冒险型三种经营方案的生产成本Bi(i=1,2,3);(2)皮靴生产厂家和专业气象台通过分析往年的气候状况,再对比当年皮靴销售状况,确定两种自然状态下的皮靴销量Lj(j=1,2);(3)皮靴生产厂家确定两种自然状态下皮靴的单价Mj(j=1,2),计算两种自然状态下的销售额Ej=Lj*Mj(j=1,2);(4)分别计算三种经营方案在两种自然状态下的预期益损值,得到益损矩阵Vi,j=Ej-Bi(i=1,2,3;j=1,2)。对照表 1,本案例的益损矩阵V为:
| $ V = \left[ {\begin{array}{*{20}{c}} {80}&{70}\\ {140}&{50}\\ {200}&{ - 90} \end{array}} \right] $ |
其中,Vi,j为经营方案di(i=1,2,3)在自然状态Sj(j=1,2)下的预期益损值。
步骤2:根据企业对待风险的偏好类型,确定经营方案。
(1) 大中取大法(或称为乐观型)
对未来出现的自然状态取乐观态度。首先从不同状态的vij中取最大值:则经营方案d1取S1状态,益损为80万;方案d2取S1状态,益损为140万;经营方案d3取 S1状态,益损为200万。再从不同方案中选取最大收益的方案。由于d1<d2<d3,按照大中取大法,应选取经营方案d3为最佳决策方案。
(2) 小中取大法(或称为保守型)
对未来出现的自然状态取保守态度。首先从不同状态的vij中取最小值:则经营方案d1的取S2状态,益损为70万;经营方案d2的取S2状态,益损为50万;经营方案d3的取S2状态,益损为-90万。再从不同方案中选取最大益损的方案。由于d1>d2>d3,按照小中取大法,应选取经营方案d1为最佳决策方案。
(3) 等概率法
对未来不同自然状态出现的概率取折中态度。在等概率原则下,可先将各不同方案的所有自然状态的益损求和,得:经营方案d1的合计益损为80+70=150万;经营方案d2的合计益损为140+50=190万;经营方案d3的合计益损为200-90=110万。再从各方案中选取合计益损最大的方案。由于d2>d1>d3,按照等概率法,应选取方案d2为最佳决策方案。
(4) 最小后悔值法
从益损矩阵中计算后悔值,即机会损失值Rij=v*j-vij。上式中v*j表示对状态Sj而言的最佳决策的益损值;vij表示状态Sj、方案d i相应的益损值。三个备选经营方案的机会损失值见表 2。
|
|
表 2 三个备选经营方案的机会损失(单位:万元) |
对应不同经营方案,选取最小的后悔值。则经营方案d1的最大后悔值为120万;经营方案d2的最大后悔值60万;经营方案d3的最大后悔值160万。最后从最大后悔值中选取后悔值最小的那个方案。由于d3>d1>d2,按最小后悔值原则,应选取方案d2为最佳决策方案。可见,最小后悔值法实际上也是悲观态度决策法之一。
2.2 确定型决策方法事实上,在未来自然状态出现的概率完全未知时,根据气象服务对象的经营风格而采取的服务策略,从某种意义上说只是一种服务技巧。另一种更重要的情形是,气象部门通过天气预报或短期气候预测,给出未来天气的变化情况,发布专业气象服务信息。对于这种确定型决策问题,可采取最大期望值决策法。其原理如下:
假设n为自然状态数目,P(Sj)表示自然状态Sj的出现概率,则有P(Sj )≥0,(j=1, 2, …, n);于是
| $ \sum\limits_{j = 1}^n {P\left( {{S_j}} \right) = P\left( {{S_1}} \right)} + P\left( {{S_2}} \right) + \cdots + P\left( {{S_n}} \right) = 1 $ | (1) |
则各方案dj的益损期望值为:
| $ EV\left( {{d_i}} \right) = \sum\limits_{j = 1}^n {P\left( {{S_j}} \right) * {V_{ij}}} $ | (2) |
期望值最大的方案,可选为最佳方案。下面用案例2进行说明。
案例2:某皮靴生产厂家在本地专业气象台的协助下制定未来冬季的生产经营策略。若气象部门预测为暖冬,则生产厂家会减少皮靴的生产规模,采取保守型经营策略d1;若为平常的冬季,则会采取适中的生产规模,采取稳健型经营策略d2。若预测为冷冬,则会扩大皮靴的生产规模,采取冒险型经营策略d3。假设冷冬出现的概率通过短期气候预测可知为 P。问如何选取最佳服务方案?
步骤1:同案例1,与生产厂家一起,确定各方案在不同自然状态下的益损值
假定专业气象台首先通过短期气候预测,得出未来出现冷冬(记为S1)的概率,P(S1)=0. 8;那么未来不出现冷冬的概率P(S2)=1-0.8=0.2。据此估算,两种自然状态下预期的益损值如表 3所示。
|
|
表 3 三个备选经营方案的预期益损值(单位:万元) |
益损矩阵V为
| $ V = \left[ {\begin{array}{*{20}{c}} {80}&{70}\\ {140}&{50}\\ {200}&{ - 90} \end{array}} \right] $ |
步骤2:计算最大期望值
利用计算公式(2),可以算出各种经营方案的益损期望值:
| $ \begin{array}{l} EV\left( {{d_1}} \right) = 0.8 \times 80 + 0.2 \times 70 = 78万元;\\ EV\left( {{d_2}} \right) = 0.8 \times 140 + 0.2 \times 50 = 122万元;\\ EV\left( {{d_3}} \right) = 0.8 \times 200 + 0.2 \times \left( { - 90} \right) = 142万元; \end{array} $ |
三种方案中,d3产生的期望值最大,即为最佳方案。
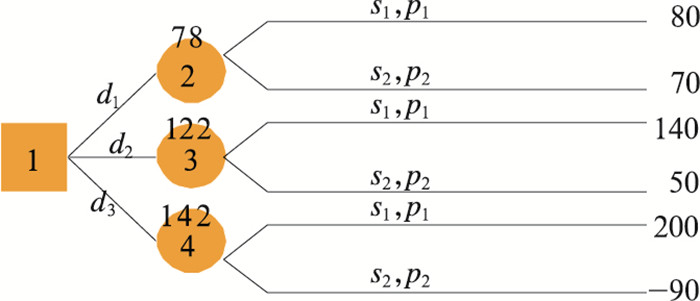
为了直观地做出决策,可采用决策树进行直观显示。决策树由结点和树枝构成:决策结点用□表示,由它生出方案枝;各方案分别生出状态结点,用○表示,由状态结点引出各种状态分枝,分枝末梢绘上相应的益损值。这样决策树模型计算结果图如下所示。
|
图 2 三种气象服务方案的决策树模型计算结果图 |
计算各个状态结点的期望值,从中选取一个最大值,往回找对应的方案为最佳方案。利用上述决策树,④点最大,d3为最佳方案。
2.3 灵敏度分析对于风险决策问题,其各个方案的期望益损值是建立在对状态概率预测的基础上。由于状态概率的预测会受到许多不可控因素的影响,因而基于状态概率预测结果的期望值也不可能同实际情况完全一致。概率的变动,可能会影响最佳决策方案的选择。这样对概率变动是否会影响最佳决策方案进行分析,就是灵敏度分析。案例2的灵敏度分析,实际上就是一个确定临界概率的数学问题。
由于案例2只涉及两种自然状态,则可采用图解法,求解各方案临界的自然状态概率值;再根据自然状态的预测概率,给出最佳经营方案。假设自然状态S1的概率P(S1)=P,则自然状态S2的概率P(S2)=1-P。则三个方案的收益期望值EV分别为:
| $ \begin{array}{l} EV\left( {{d_1}} \right) = {V_{11}} * {P_1} + {V_{12}} * {P_2}\\ EV\left( {{d_2}} \right) = {V_{21}} * {P_1} + {V_{22}} * {P_2}\\ EV\left( {{d_3}} \right) = {V_{31}} * {P_1} + {V_{32}} * {P_2} \end{array} $ |
代入P1=P,所以P2=1-P,得
| $ \begin{array}{l} EV\left( {{d_1}} \right) = \left( {{V_{11}} - {V_{12}}} \right) * P + {V_{12}}\\ EV\left( {{d_2}} \right) = \left( {{V_{21}} - {V_{22}}} \right) * P + {V_{22}}\\ EV\left( {{d_3}} \right) = \left( {{V_{31}} - {V_{32}}} \right) * P + {V_{32}} \end{array} $ |
显然3种方案的期望收益值是三个以P为未知数的一元函数。为了方便,写成如下格式:
| $ \begin{array}{l} {y_1} = {k_1}x + {m_1}\\ {y_2} = {k_2}x + {m_2}\\ {y_3} = {k_3}x + {m_3} \end{array} $ |
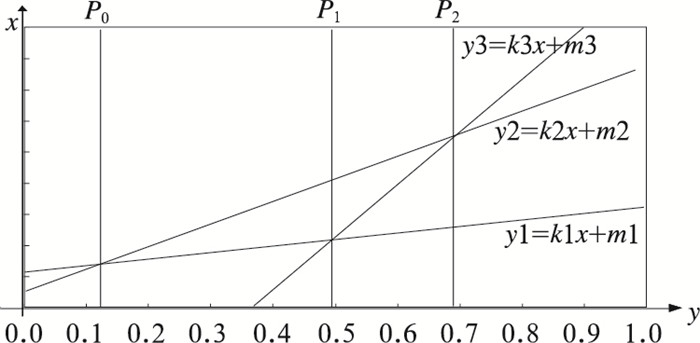
这里x为自然状态出现的概率P。这样决策树问题“EV的期望值最大”转化为“不同x的区间时,y的数值最大”数学问题。利用图解法(图 3),三条直线y1、y2和y3两两交叉,三个交点的横坐标分别为P0,P1,P2。
|
图 3 图解法 |
从图 3可见,当自然状态概率0.0<x<P0时, y1取最大值,对应d1最佳经营方案;当自然状态概率P0<x<P2时, y2取最大值,对应d2为最佳经营方案;当自然状态概率P2<x<1.0时, y3取最大值,对应d3为最佳经营方案。
对于案例2,由图解法知临界概率值P0=0.25,P2=0.70。假如未来出现冷冬的概率在(0, 0.25)之间, d1为最佳经营方案;假如出现冷冬概率在(0.25, 0.70]之间,d2为最佳经营方案;假如在(0.70,1.0]之间d3为最佳经营方案;假如冷冬概率为临界值P0=0.25时,d1和d2同为最佳经营方案;假如冷冬概率为临界值P0=0.70时,d 2和d3同为最佳经营方案。
3 结论(1)当未来高影响天气状态的概率未知时,根据服务对象对待风险的偏好,选择合适的服务方案。对乐观型服务对象,可采取大中取大法进行决策;对保守型服务对象,可采取小中取大法或最小后悔值法进行决策;对中性服务对象,可采取等概率法进行决策。不确定型风险决策,既体现了准确可靠的气象服务信息对用户的重要作用,同时气象服务中要根据服务对象运用适当的服务技巧。
(2)当未来高影响天气出现的概率已知时,若不考虑服务对象对待风险的偏好,可直接采用最大期望值方法进行决策,选取最佳气象服务方案。若需考虑服务对象对待风险的偏好,可进一步期望效用分析,选取最合适的气象服务方案。这也间接体现了气象精细服务的巨大潜能和需求,即在气象服务质量稳步提高的同时,其影响将逐步深入到国民经济各个行业,参与用户决策、管理等多个经营环节,产生较佳的社会经济效益。
| [1] |
陈□. 随机决策分析[M]. 北京: 科学出版社, 1987.
|
| [2] |
徐建华. 现代地理学中的数学方法[M]. 北京: 高等教育出版社, 2002: 204-222.
|
| [3] |
张志娟. 贷款融资的多目标随机决策模型[D]. 硕士学位论文. 河南大学, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10475-2007145358.htm
|
| [4] |
张智光. 离散与连续混合多变量随机决策方法及其在水环境—经济系统中的应用[C]. 全国青年管理科学与系统科学论文集(第1卷), 1991: 325-331. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGXC199110001056.htm
|
| [5] |
吴琦, 熊光泽. 基于随机决策模型的动态功耗管理策略研究[J]. 计算机学报, 2007, 30(4): 622-628. |
| [6] |
冯俊文. 多目标随机决策方法研究及其在R&D项目选择中的应用[J]. 系统工程理论与实践, 1991(6): 60-66. |
| [7] |
郑健壮, 王培才. 经济学基础[M]. 北京: 清华大学出版社, 2004: 176-178.
|
 2008, Vol. 34
2008, Vol. 34