天气预报技术在大气科学及相关学科进步的推动下得到迅猛发展,各种气象服务产品的功能和性能不断增强和提高,产品的空间分辨率逐渐精细化,高时间分辨率的短时临近预报产品也层出不穷。社会公众对气象服务的需求也随着国民经济的发展而变化。Kelly认为“公众如不能及时、有效地获得预报信息,即使是最完善的天气预报技术也只能是学术练习”[1],可见满足公众的需求是气象服务的第一目标。气象服务产品能否满足公众、行业、政府及重大社会活动的需求,成为其进一步改进和发展的前提和基础。世界气象组织世界天气研究计划(WWRP)发起的国际天气预报示范项目(FDP),已在近几届奥运会期间做了示范性运用,目的在于检验各种预报产品对奥运气象服务保障的功能和效果,根据用户反馈的信息改进预报技术,提高预报产品的服务质量[1-4]。WWRP同样将在北京2008奥运期间实施FDP产品的示范性应用及检验。FDP产品的社会经济效益评估是示范计划的重要组成部分,这项工作极富挑战性。社会调查是评估工作的基础,它直接获得公众或行业用户对现有气象服务的评价。评估工作的难点是目前还没有一套系统的、规范的定量评估方法能有效地从社会调查资料中提取、归纳出有价值的信息和知识,多数情况下依然延续使用定性的处理方式,比如至今仍在使用的Delphi法[5-6]。Satty提出的层次分析(AHP)模型是一种将定性与定量分析相结合的方法[7]。模型的数据组织、结构和计算特点符合评估的目的和要求。评估所用的指标采用的是一种多层次、树状的体系结构,AHP模型能有效利用这类指标的数据特点分层次地计算各层指标的组合权重。将AHP方法应用于气象服务评估仍有许多改进之处,尤其在多指标对比下的权重计算仍然繁琐。研究个例依据社会调查资料中指标的公众得票率来初始化指标的权重系数,从而简化了AHP的处理过程。
1 层次分析(AHP)模型原理层次分析模型(AHP)将评估过程中相关因子分解成目标、准则、方案等层次(如图 2),将解决问题的思维层次化和数量化,用数学方法进行描述,从而为求解多目标、多准则或无结构特性的复杂评估问题,提供一种实用、简便的定量化方法[7-10]。AHP从底层指标的权重计算“自低向上”逐步收敛到顶层的权重系数,权重系数结果的可信度最终受到低层指标权重系数准确度的制约。AHP模型应用受到的最大限制是底层指标权重的成对比矩阵换算,由于涉及指标多,容易造成一致性检验无法通过的情况。气象服务社会经济效益评估的底层指标的权重值直接由用户支持率来设定,是真实情况的反映,因此能保证评估结果的可信度。AHP模型的计算过程如下。

|
图 2 气象服务社会经济效益评估层次结构图 |
假设要比较某一层n个指标C1, C2,…,Cn,每次取两个指标Ci和Cj进行比较,用aij表示Ci相对Cj的重要程度,这种比较结果可用成对比较矩阵
| $ \mathit{\boldsymbol{A}} = {\left( {{a_{ij}}} \right)_{n \times n}}, {a_{ij}} > 0, {a_{ji}} = 1/{a_{ij}} $ | (1) |
表示,由于式(1)给出的aij的特点,A又称为正互反矩阵,aij=1。
1.2 设置指标因素之间的比较尺度根据评估的目的和要求,确定制约气象服务产品准则层、准则层-方案层面上各指标的比较尺度。aij一般取1,3,5,7,9等5个等级尺度,1表示Ci同Cj同等重要;3表示Ci较Cj重要一点;5表示Ci较Cj重要得多;7表示Ci较Cj更重要;9表示Ci较Cj极端重要;2,4,6,8表示相邻判断的中值。
1.3 对比矩阵权重向量计算层次分析中诸指标C1,…,Cn对上层指标的权重对应于成对比矩阵A的特征根n的归一化特征向量,即对应于A的最大特征根(λ)的特征向量(归一化后)作为权向量W,W满足AW=λW。
因为成对比较阵是通过定性比较得到的比较粗糙的量化结果,可以采用简便的近似方法计算其特征根和特征向量,这里选用根法计算,方法如下:将A的每一列向量归一化得
成对比矩阵需要一致性检验。n阶一致阵的特征根是n,λ=n时A是一致阵,λ比n大得越多,A的不一致程度越严重,可以用λ-n数值的大小来衡量A的不一致程度,CI=(λ-n)/(n-1)为一致性指标,CI=0时A为一致阵;CI越大A的不一致程度越严重。
定义1(随机一致指标RI):随机构造正互反阵A′,用它们的CI的平均值作为随机一致性指标。随机一致性指标RI可以查取事前定义的查找表。
定义2(一致性比率CR):对于n≥3的成对比较阵A,将它的一致性指标CI与同阶(n相同)的随机一致性指标RI之比称为一致性比率CR。
当CR=CI/RI<0.1,认为A的不一致程度在容许范围内,可用其特征向量作为权向量。
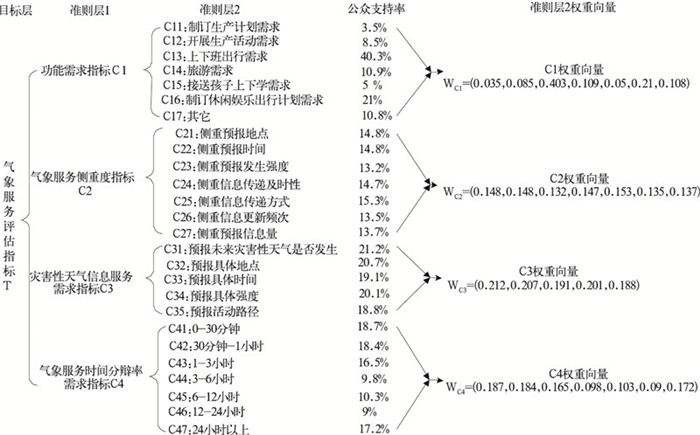
2 建立在用户需求基础上的层次分析(AHP)评估模型应用 2.1 评估指标及评估层次结构AHP方法在准则层指标较多、指标间有多层嵌套关系的情况下,很难保证成对比矩阵的一致性,这就需要反复修改指标之间的对比值,反复进行一致性检验。在指标较多的情况下,创建合理、有效、一致性检验合格的成对比矩阵极不容易,而且涉及指标越多难度越大,这时单纯采用层次分析方法非常缺乏可操作性及实用性。结合社会调查资料的AHP模型的优势在于准则层低层次上的指标权重根据社会调查资料来确立,即由该指标得到公众的支持率来确定,避免因为一致性检验所引起的指标权重计算较复杂的问题,这样的权重系数更能真实反映公众实际需求情况。当然,“准则层”较高层次上的指标从定性到定量转变仍用成对比矩阵求取。AHP中较高层次的指标数量一般较少,比较容易掌握,比如“准则层1”(图 1、2)只涉及4个指标,用AHP方法计算权重向量就相当简便。
|
图 1 气象服务社会经济效益评估指标体系结构及权重系数图 |
Delphi及其变种方法[6-7]是气象服务社会经济效益评估常用的方法。它原则上统计用户对评估指标的期望得分与实际得分来比较服务产品各自对用户需求的满足程度,形式上也使用问卷式社会调查的方法来获得统计信息。Delphi法的最大缺陷是没有严格区分不同指标意义下应该存在的不同权重,其单纯的累加分值一般不具备可比性,比如在产品空间分辨率指标上的50分就不能完全等同于时间分辨率指标上的50分,将二者无量纲相加的结果是无意义的。AHP模型计算多层指标的组合权重值,将评估结果统一到相同的量纲上,结果是合理的、可比的。图 1为评估指标体系结构及权重系数图,图 2为气象服务社会经济效益评估AHP模型的层次结构图。本研究低层指标Cij的各项权重的换算结果是建立在4351份公众访谈式问卷的基础上,其中
| $ {C_{ij}}权重值 = \frac{该项指标的得票数}{公众的投票总数} $ |
计算的权重系数值见图 1。
2.2 基于AHP的气象服务产品社会经济效益评估个例计算方法及步骤步骤1:设置方案层备选方案:P1:常规气象服务产品;P2:充当奥运气象服务主力的FDP产品。
步骤2:计算方案层P1、P2对应准则层2各项指标的相对权重(层次单排列),因为只求解两个方案对应单个指标的2×2成对比矩阵的特征根和特征向量,计算简便,比如P1、P2满足C11的权重值计算就用表 1所列的判断矩阵来完成,成对比矩阵对比值的设置采用专家打分法。
|
|
表 1 P1、P2满足C11判断矩阵 |
权重越大表明方案越能满足准则层2的各项指标要求,采用上述方法,P1、P2对应准则层2指标的权重计算结果如表 2。
|
|
表 2 P1、P2对应准则层2指标权重表(i=1, 2, 以下各表同). |
步骤3:利用专家打分方法,以层次分析模型的比较尺度为度量基准,建立准则层1各项指标的成对比矩阵(表 3),算出矩阵特征值λ、特征向量(权重系数)——准则层1权重向量WC及一致性检验CR,结果见表 3。
|
|
表 3 T—C判断矩阵及层次排序结果表 |
步骤4:在步骤2的基础上计算方案层P1、P2对应准则层1的组合权重,如表 4所示。
|
|
表 4 P1、P2对应准则层1指标组合权重值表 |
步骤5:P1和P2的社会经济效益评估值分别等于WP1-C、WP2-C与准则层1的AHP分析所得的权重向量(表 3)WC=(0.269,0.121,0.42,0.19)T的乘积(组合值),即(表 5)
|
|
表 5 计算结果表 |
Rp2>Rp1,定量计算结果表明方案FDP产品比常规气象服务产品更能满足公众对气象服务的需求。
2.3 结果讨论与分析(1) 个例应用中AHP的准则层为二层结构,底层(准则层2)权重系数WC1、WC2、WC3、WC4根据社会调查资料中公众对每项指标的投票支持率来标定,没有用专家打分后的成对比矩阵计算。权重值以用户需求为导向,是用户对服务需求的直接反映,在某种程度上比专家打分更有说服力,而且避免反复进行成对比矩阵的一致性检验,更加容易操作。
(2) 准则层1—4项指标的权重系数是经由专家打分后所形成的正互反矩阵的特征向量确定。AHP方法计算后的特征向量WC=(0.269,0.121,0.42,0.19)T为各项指标的权重(表 2),其一致性检验CR=2.624E-02 < < 0.1,说明在各项指标的重要性对比上,成对比矩阵的一致性检验合格。需要特别注意的是为体现安全奥运的要求,侧重2008北京奥运气象安全服务的目的和要求,特将灾害性天气信息服务需求指标的重要性提到首位;鉴于天气状况及条件对奥运比赛项目有直接的、特殊的影响,现代体育运动要求气象服务能尽量提供较高时间分辨率的天气预报产品,特将气象服务时间分辨率需求指标列到较重要位置。最后计算的权重系数是指标重要程度前后排列的定量化结果。
(3) AHP方案层拟定常规气象服务和FDP产品两个备选方案,它们在准则层1和准则层2两层指标的逐层分析中所计算出的权重值是对其服务功能满足用户需求程度的定量评估结果。评估表明:(a)有中长期天气预报服务特点的现有气象服务比较容易满足生产、生活及娱乐计划制订等系列的用户需求,但在短时、临近事务性质的需求上,比如上下班出行需求、接送小孩需求等,中长期天气预报就显得无能为力。而FDP产品时间分辨率较高,基本能满足这类需求。常规天气预报产品要在短时临近预报需求指标上拿较高分值,应结合短时临近预报技术,提供多样化、高时间分辨率的预报产品。(b)在气象服务的侧重度指标上,用户对准确、详细的预报地点指标有一定的要求,尽管现有数值预报模式能提供3km格点大小的数值预报产品,但这个标准恐怕还不能完全满足公众的需求。采用新一代雷达技术的FDP产品在空间分辨率、信息更新频次及预报信息量上有一定的优势,只是其预报时间间隔短,无法像中长期预报那样有较长的信息传递准备周期。因此,丰富FDP等短时临近预报的信息传递方式,提供及时、有效的天气预报信息是现有短时临近预报产品需要重点改进的地方。
(4) FDP产品以灾害监测为首要目标,能提供0~3小时的预报。在灾害性天气信息服务需求指标、气象服务时间分辨率需求指标上,有得天独厚的优势,这也说明FDP等短时临近预报产品是奥运气象服务的主力军,是奥运气象安全的重要保障。
3 结语(1) 采用社会调查所获取的用户需求信息对AHP准则层2的诸指标权重赋值,既体现气象服务用户需求驱动的观点,又简化了操作流程;采用层次分析(AHP)模型,用专家打分法对准则层1指标进行重要性对比,建立一致性(一致性检验合格)成对比矩阵,计算矩阵的特征向量即为指标的权重向量。为充分体现安全奥运及奥运气象服务的要求,专家打分适当向灾害性天气信息服务需求指标和气象服务时间分辨率需求指标倾斜。
(2) 选用常规气象服务产品及FDP产品作为方案层的两个备选方案。AHP逐层收敛计算成对比矩阵的特征向量及组合权重,结果表明FDP产品比常规气象服务产品更能满足公众对气象服务的要求。并得出如下结论:现有天气预报需要吸纳短时临近预报技术,提供多样化、高时间分辨率的气象服务产品;丰富FDP等短时临近预报的信息传递方式,提高信息传递的及时性和有效性是现有短时临近预报产品需要强化的内容。
(3) AHP结合公众反馈信息的评估方法科学合理,将定性指标定量化,即克服AHP方法在多指标情况下需要反复检验指标对比一致性的弊端,又能将多层次、多结构的指标按权重逐级收敛,组合换算成可比的统一量纲结果值。
| [1] |
Rothfusz L. P, Mclaughlin M. R, Rinard S. K. An Overview of NWS Weather Support for the XXVI Olympiad[J]. Bull. Amer. Meteor. Soc, 1998, 79(5): 845-860. DOI:10.1175/1520-0477(1998)079<0845:AOONWS>2.0.CO;2 |
| [2] |
Johnson J. T, Eilts M. D, Ruth D, Goodman W, Rothfusz L.P. Warning Operations in Support of the 1996Centennial Olympic Games[J]. Bull. Amer. Meteor. Soc, 2000, 81(3): 543-554. DOI:10.1175/1520-0477(2000)081<0543:WOISOT>2.3.CO;2 |
| [3] |
Linda Anerson-Berry, Tom Keenan, John Bally, et al. The Societal, Social, and Economic Impacts of the World Weather Research Programme Sydney 2000 Forecast Demonstration Project (WWRP S2000 FDP)[J]. Weather and Forecasting, 2004, 19(2): 168-178. |
| [4] |
Elly Spark. Report on Weather Services for the Sydney 2000 Olympic Games[R]. 2002.
|
| [5] |
周福. 德尔斐法在行业气象服务效益评估中的应用及结果分析[J]. 浙江气象科技, 7(3): 1996. |
| [6] |
罗慧, 谢璞, 俞小鼎. 奥运气象服务社会经济效益评估个例分析[J]. 气象, 2007, 33(3): 89-94. DOI:10.7519/j.issn.1000-0526.2007.03.013 |
| [7] |
Satty T. The Analytical Hierarchy Process[M]. New York: Mcgraw-Hill, 1980.
|
| [8] |
秦寿康. 综合评估原理与应用[M]. 北京: 电子工业出版社, 2003.
|
| [9] |
马东辉, 郭小东, 苏经宇, 等. 层次分析法逆序问题及其在土地利用适宜性评价中的应用[J]. 系统工程理论与实践, 2007, 27(6): 124-135. |
| [10] |
张继权, 刘兴奋朋, 佟志军. 草原火灾风险评价与分区——以吉林省西部草原为例[J]. 地理研究, 2007, 26(4): 756-761. |
 2008, Vol. 34
2008, Vol. 34