2. 国家气象中心
2. National Meteorological Center
集合预报能较好地预报大气运动的不确定性,但由于模式误差的存在,模式长期积分会趋向于内在的统计平衡状态,出现系统误差。为改进预报效果有必要在使用集合预报之前用后处理的方法剔除系统误差。贺皓[1]曾对T42数值预报产品进行订正,其中高度场和温度场采用不同时间权重和空间平滑的订正方案,风场采用动力订正方案, 湿度场采用平流(风场)订正方案,取得了较好的效果;1998年魏文秀等[2]用卡尔曼滤波技术对500hPa高度场进行了多种订正试验,证明卡尔曼滤波双因子订正对于提高暴雨中期预报能力是有效的;2005年任宏利等[3]利用历史资料的相似信息直接估计当前模式误差的反问题, 发展出一种将统计和动力两种方法有机结合的相似误差订正。2006年李莉等[4]通过统计学的方法对T213降水预报进行订正,订正后预报偏差有明显改善,雨带的位置和轮廓更加接近降水实况。
订正后的集合预报虽然给出了大气运动各种较可能的状态,但对绝大多数的预报服务对象而言,并不期望得到一个似是而非的预报结论。这就存在一个由集合实现集成的问题。Krishn amurti等[5-6]同时考虑了初始场和模式的不确定性,提出了多模式超级集合预报思想,即使用多个模式的结果,每个模式都有其自身的子集合预报系统,并依据一定的方法对预报结果进行集成,以获得最佳决定性预报。2003年杨松等[7]对误差订正后的几种预报结果进行简单的算术平均集成以消除随机误差,预报结果明显改善;陈丽娟等[8]用超级集合的思想对参加中国汛期降水预测的各大单位预报结果进行集成,利用线性反演技术进行正反拟合和预报试验,集合预报效果比较稳定,多数情况下优于单个成员预报;2005年赵声蓉[9]基于中国T213模式、德国气象局业务模式和日本气象厅业务模式2m温度预报,利用BP神经网络建立了温度集成预报系统,集成结果明显优于3个模式单独的预报结果。
基于订正系统误差,提炼最优预报的目的,本文对5个区域集合预报模式的2m温度预报结果进行误差订正,并以订正后的预报结果做算术平均和多元线性回归两种方法的多模式集成试验。
1 资料使用的2m温度预报分别来自于中国国家气象中心(记为NMCC,下同)、日本气象厅(JMAA)、美国国家环境预报中心(NCEP)、加拿大气象中心(MSCC)以及澳大利亚-法国气象局(ZAMG)的区域集合预报模式。预报区域为105°~125°E,30°~45°N,模式分辨率是0.15°×0.15°,预报时效为36小时内每3小时间隔。资料选用各模式在2007年7月24日—8月2 4日每天12时(世界时)起报的2m温度预报结果和我国400个站1日8次的温度观测资料(图 1)。为了便于预报员直接使用,并减少插值过程产生的误差,采用格点预报结果插值到站点的方式进行相关研究。
|
图 1 预报区域与站点分布情况 |
模式误差是预报误差的主要来源之一。虽然正面改进模式各个环节来发展模式非常重要,但模式终究不能达到完美,发展经验性方法来减小模式误差对预报的影响是非常必要的。目前的模式误差订正方法大体可分成两类[10]:一是后验(或事后)订正;另一是过程订正。本文采用Cui Bo等提出的通过滞后平均降低误差尺度的自适应(卡尔曼滤波类型)误差订正方法,属于后验订正,即只在整个积分完成后对预报结果进行订正处理。该套方法最初被用于美国NCEP全球集合预报系统的误差订正。现把该方法用于区域集合预报系统,并评估其在区域集合预报系统中的表现。
2.1 方法和步骤首先,用双线性插值方法把各模式2m温度预报结果插值到400站,记为ai(t),计算预报在各站点i各时次t的集合平均fi(t);
其次,估算误差bi(t)。公式(1)中ai(t)为t时刻的观测结果,fi(t0)为与t时刻观测结果对应的t0时刻预报结果。
| $ {b_i}\left( t \right) = {f_i}\left( t \right) - {a_i}\left( {{t_0}} \right) $ | (1) |
再次,选择适当的权重系数,计算滞后平均Bi(t)。鉴于区域模式预报时效短,范围小的特点,选取w=0.05,0.1和0.15进行试验,并最终选定w=0.1作为权重系数,相应的使用过去10到20天的历史资料[11]。当t=1时实行冷启动, 即Bi(t-1)=0。之后,不断把前一天同一时次计算得到的Bi(t-1)迭代到方程(2)中,计算当下时次的误差Bi(t)值。
| $ {B_i}\left( t \right) - \left( {1 - \omega } \right){B_i}\left( {t - 1} \right) + \omega {b_i}\left( t \right) $ | (2) |
最后, 做误差订正预报Fi(t)。即在初始模式预报中扣除通过历史资料算出的误差。
| $ {F_i}\left( t \right) = {f_i}\left( t \right) - {B_i}\left( t \right) $ | (3) |
理论上取w=0.1时使用过去10到20天的历史资料,即误差通过十来天的迭代应该趋于收敛、稳定。试验表明,从2007年7月24日开始误差迭代计算,到8月5日误差确实已经收敛稳定,且5个模式均没有出现随时间推移而误差发散的迹象,说明试验设计是合理可行的。下面以NMCC区域集合预报模式为例,对2007年8月5—24日的误差订正结果做检验分析,用不同指标来评价误差订正的效果。
2.2.1 集合平均的平均绝对误差温度预报的平均绝对误差是衡量预报效果的根本指标。图 2中,订正后各时效预报的绝对误差都有所减小,减小幅度在6小时高达30%,订正效果有随预报时效的延长而降低的趋势。此外,绝对误差存在明显的日变化,一般是白天的预报误差相对较大,夜间的预报误差相对较小,这与温度本身的变化特点有关。
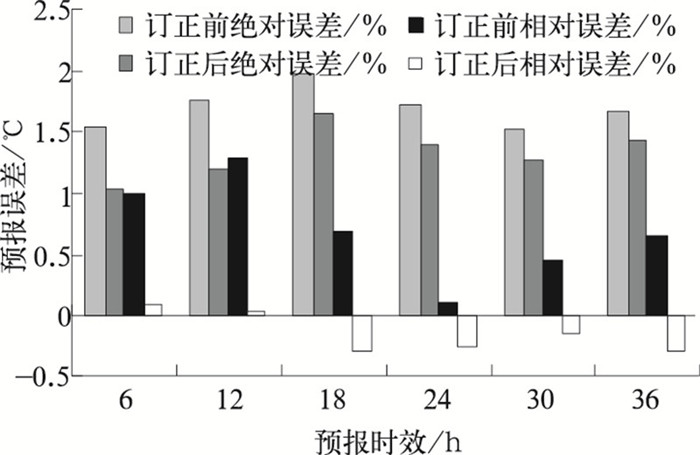
|
图 2 2007年8月5—24日订正前后2m温度的平均绝对、相对误差 |
平均绝对误差反映了温度预报的一个重要方面,而相对误差反映的是预报的系统误差情况。图 2中除24小时预报外订正后的平均相对误差都有所减小, 总的来说系统误差减小了;预报的平均相对误差以负值居多,说明模式温度预报以偏低为主;而订正对各成员预报的改善程度则可由集合成员的相对误差时序图看出。下面以6小时预报(对应北京时间02时)和18小时预报(对应北京时间14时)为代表,分析NMCC模式各集合成员预报逐日的相对误差情况。
我们知道集合预报的目的之一是提供预报的可靠性。如果集合预报成员间差别很大,那么很明显至少其中有些预报是错误的,反之,则有更多的理由相信所做的预报。所以订正前NMCC模式的成员预报相对误差出现图 3中两簇分化的情况就预示了集合预报系统存在的一些问题。而误差订正过程是否对这一问题有所改善呢?图 3b、d可以看出,两簇分化的现象得到有效改善,表明误差订正在现有模式的基础上改进了预报效果,预报更为可信。其它4个时次的集合成员预报分簇现象不那么明显,订正效果同样可观(图略)。此外,图 3b、d中,相对误差均在零值线上下波动,表明订正过程对矫正系统误差起了很大作用,订正后的系统误差不明显,这与图 2得到的结论是一致的。
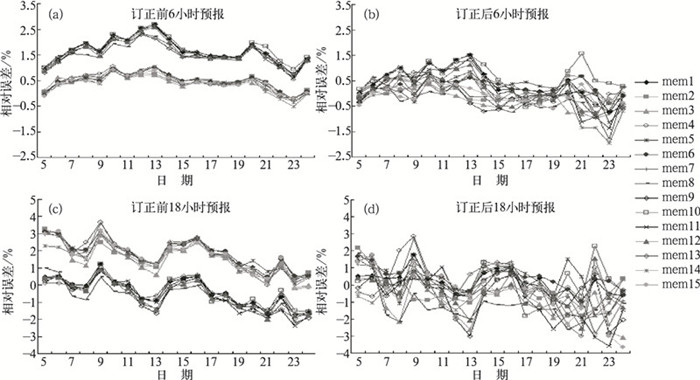
|
图 3 2007年8月5—24日订正前后集合成员的2m温度预报相对误差时序图 |
一个理想的集合预报系统,应该能表现出成员所有可能的状态[12],一般用集合成员与平均之间的离散度来衡量,反映了预报的不确定性、置信度和集合成员总体变率程度,在一定意义上可代表预报技巧。一般来说,离散度小,预报技巧高,预报可信度高。而离散度则可用均方根误差来衡量,好的预报两者应该是相当的。从图 4可以看出,误差订正使均方根误差有所减小,减小幅度在06时高达30%,且与离散度曲线更逼近, 说明订正后的预报提供了未来大气的一种较好的可能性,但仍存在离散度过小的情况。
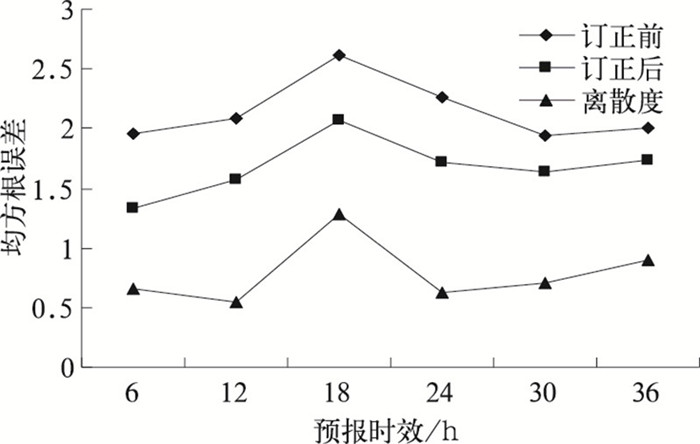
|
图 4 2007年8月5—24日2m温度的平均均方根误差和离散度 |
Talagrand分布图是一种必须的检验手段,用来衡量预报值和检验值是否来自相同的概率分布[13]。O.Talagrand[14]认为一个“好”的集合预报系统的标准是每个成员似乎以相同的概率发生,Talagrand分布图应该是平直的;换言之,观测实况也应以相同的概率落在每个成员附近。图 5中可看到,订正后talagrand分布有所平缓,观测实况落在第9区间的概率高于周围区间的异常也得到改善,但U型分布的情况仍然存在,说明集合预报成员间的发散度不够,这也是目前集合预报普遍存在的问题。
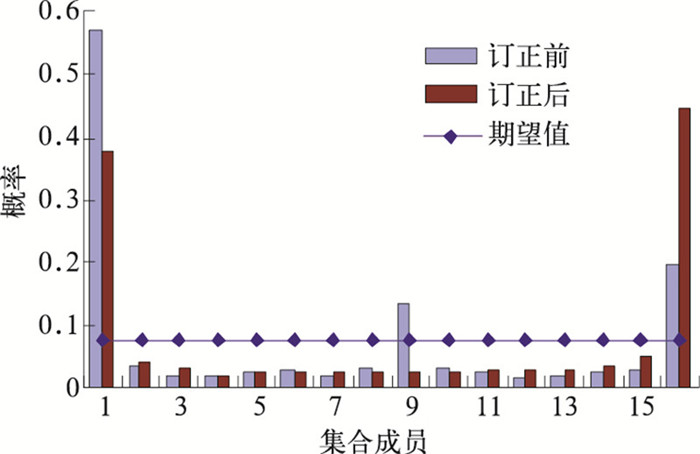
|
图 5 2007年8月5—24日订正前后2m温度的6小时预报talagrand分布 |
随着预报技术的发展和国际间交流合作的加强, 我们能获得的气象资料越来越丰富。集成作为一种博采众长,去粗取精的有效手段,充分利用统计方法和历史资料对参考信息进行分析,能较好地提炼有价值的预报,改善预报效果。集成预报主要强调两个方面的内容,其一是每个集合成员中所包含的可用信息都要得到最大限度的提取和利用;其二是必须实现综合集成预报效果总体上是最好的,其预报产品的性能稳定[15]。确立算术平均和多元线性回归两种方法进行多模式集成试验,分析集成对提高预报能力的影响。
3.1.1 算术平均集成预报法对5家预报产品取平均,做为集成后的预报结果。在预报样本量不是足够大的情况下, 算术平均集成法通常不能得到最优集成预报。但计算简便,效果稳定,在集成研究中仍被广泛使用。
3.1.2 多元回归集成预报法以n个预报工具的p次预报产品做回归集成的因子,以对应的实际观测值作为集成变量,设法找出最能代表它们之间关系的数学表达形式, 进行预报集成。在有限样本情况下, 回归系数可以保证在最小方差意义下得到最优集成拟合[16]。虽然多元回归集成满足统计意义上以集成预报误差极小的约束条件,但是否能够保障其预报效果是最好的,是否能保障在p次预报试验以外的任何一次预报中效果也最好等问题,仍有待进一步探讨。
3.2 集成结果检验分析 3.2.1 集合平均的平均绝对误差和平均相对误差表 1中,5个预报模式的绝对误差都在0.96~1.7之间,差异不明显,其中JMAA模式任何时效预报的集合平均绝对误差都最小,预报效果最好。18小时预报的绝对误差都是最大的,日变化规律明显。另外在36小时预报时效内,2种集成方法的平均绝对误差均小于各子模式预报,说明集成预报比单一模式预报更准确。从相对误差来看没有哪个模式表现比较突出,且5个模式的平均相对误差几乎全为负值,表明区域集合预报模式普遍存在2m温度预报偏低的问题。两种集成预报的系统误差都很小,且多元回归集成的系统误差小于算术平均集成。因而无论从平均绝对误差还是平均相对误差来看,多元回归集成法的预报效果都好于算术平均集成法。
|
|
表 1 子模式与集成预报的2m温度集合平均的平均绝对、相对误差(2007年8月5—24日) |
相关系数反映的是预报场与实况场的相关程度。各模式预报和集成预报的相关系数都在0.8以上,相关程度比较好(图 6)。由于预报误差日变化的原因,18小时预报的相关系数也是最低的。两种集成预报的相关系数均高于单一模式预报,且总的来说多元回归集成预报的相关系数高于算术平均集成预报。而在各子模式中,日本JMAA模式的相关系数始终是最高的。
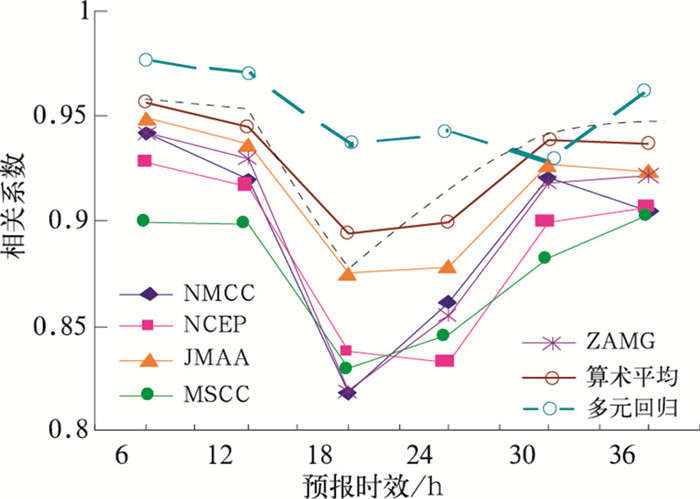
|
图 6 2007年8月5—24日子模式与集成后预报的相关系数 |
图 7可以清楚地看出集成预报的均方根误差小于任一子模式预报,且多元回归集成预报仍是优于算术平均集成预报。集成预报的离散度与图 4相比明显增大,与均方根误差曲线数值更为相近,说明多模式集成增加了集合离散度,预报可信度大为提高。其中多元回归集成预报的离散度表现为稍微偏大。从单个模式看,JMAA模式的均方根误差最小,仍是表现最好的子模式。
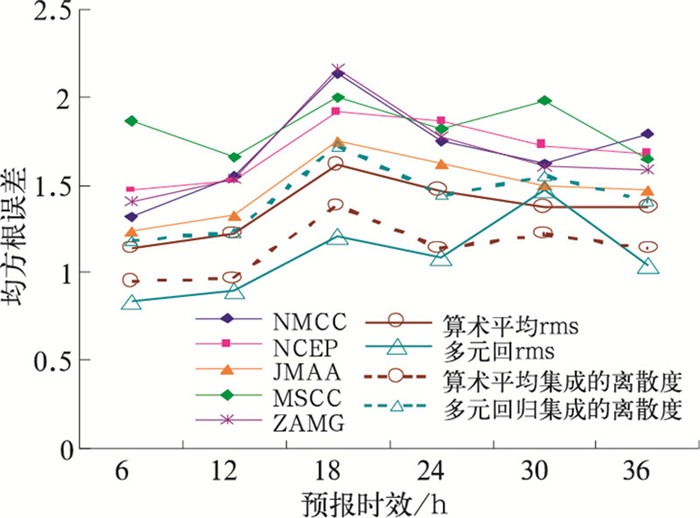
|
图 7 2007年8月5—24日子模式与集成后预报的均方根误差和离散度 |
经过对5个区域模式误差订正和多模式集成结果的检验分析,得到以下几点结论:
(1) 自适应误差订正方法在区域集合预报系统中仍然适用。NMCC模式订正后的平均绝对误差在1.8℃以内,均方根误差也有明显的减小,talagrand图的U型分布仍然存在,但个别成员异常的现象得到改善。平均相对误差从数值上看订正效果不明显,实际上模式成员分簇的现象的得到了很好的矫正。
(2) 受温度自身的变化影响,2m温度预报存在明显的日变化,白天的预报误差大于夜间。各模式对2m温度的预报都普遍偏低。在较短预报时效内误差订正效果明显,之后有随预报时效延长而降低的趋势。另外4个子模式2m温度预报的系统误差订正效果也很显著,其中日本的JMAA模式的预报结果最好。
(3) 集成预报的平均绝对误差普遍小于单一模式预报, 并且不存在明显的系统误差, 预报达到了一定的精度, 在预报业务中有较好的使用价值。两种集成方法中,多元回归法选取因子的原则是因子与预报量的相关性,最终进入预报方程的是与预报量相关性好的因子,相关性差的因子被剔除。而算术平均只是简单的对各因子取相同的权重,所以多元线性回归法的集成预报效果要优于算术平均方法。
(4) 多模式多分析初值的超级集合预报最大的优势是充分考虑了初值和模式的不确定性。但本文所做的订正、集成分析还只是简单地针对集合平均展开,没有针对模式的不确定性深入研究。因此,针对模式的不确定性进行订正、集成还有很大的发展空间,有望获得更好的预报效果。
| [1] |
贺皓. 数值预报产品系统性误差的客观订正[J]. 高原气象, 1995, 14(2): 198-206. |
| [2] |
魏文秀, 任彪, 杨海龙, 等. 卡尔曼滤波技术在暴雨中期预报中的应用[J]. 气象, 1998, 24(3): 46-49. DOI:10.7519/j.issn.1000-0526.1998.03.010 |
| [3] |
任宏利, 丑纪范. 统计-动力相结合的相似误差订正法[J]. 气象学报, 2005, 63(6): 988-993. DOI:10.11676/qxxb2005.094 |
| [4] |
李莉, 朱跃健. T213降水预报订正系统的建立与研究[J]. 应用气象学报, 2006, 17(Suppl): 130-133. |
| [5] |
Krishnamurti T N, Krishtawal C M, LaRow T, et al. Improved weather and seasonal climate forecasts from multimodel superensemble[J]. Science, 1999, 285: 1548-1550. DOI:10.1126/science.285.5433.1548 |
| [6] |
Krishnamurti T N, Krishtawal C M, Zhang Z, et al. Multi-model Superensemble Forecast for Weather and Seasonal and Seasonal Climate[R]. 1999, FSU Report 99-8.
|
| [7] |
杨松, 杞明辉, 姚德宽. 误差订正在预报集成中的应用研究[J]. 气象, 2003, 29(12): 22-24. |
| [8] |
陈丽娟, 许力, 王永光. 超级集合思想在汛期降水预测集成中的应用[J]. 气象, 2005, 31(5): 52-54. DOI:10.7519/j.issn.1000-0526.2005.05.011 |
| [9] |
赵声蓉. 多模式温度集成预报[J]. 应用气象学报, 2006, 17(1): 52-58. DOI:10.11898/1001-7313.20060109 |
| [10] |
任宏利, 丑纪范. 数值模式的预报策略和方法研究进展[J]. 地球科学进展, 2007, 22(4): 376-385. |
| [11] |
B. Cui, Z. Toth, Y. Zhu, et al. Bias correction methods-adjusting moments[R]. Preprints, European Geoscience Union General assembly 2005. Vienna, Austria, European Geoscience Union, EGU05-A-05997.
|
| [12] |
Leith .C E. Theoretical skill of Monte Carlo forecast[J]. Mon.Wea.Rev, 1974, 102: 409-418. DOI:10.1175/1520-0493(1974)102<0409:TSOMCF>2.0.CO;2 |
| [13] |
Hou D., Kalnay E., Droegemier K, K. Objective verification of the SAMEX'98 ensemble forecasts[J]. Mon. Wea. Rev, 2001, 129: 73-91. DOI:10.1175/1520-0493(2001)129<0073:OVOTSE>2.0.CO;2 |
| [14] |
Talagrand O and Vautard R. Evaluation of probabilistic prediction systems[R]. Workshop on predictability ECMWF. 1997, 10: 20-22.
|
| [15] |
杞明辉. 天气预报集成技术和方法应用研究[M]. 北京: 气象出版社, 2006: 82.
|
| [16] |
魏凤英. 全国夏季降水区域动态权重集成预报试验[J]. 应用气象学报, 1999, 10(4): 402-409. |
 2008, Vol. 34
2008, Vol. 34