2. 国家气象中心
2. National Meteorological Center
为充分表征大气运动的不确定性,集合预报往往采用不同的物理参数化方案来构造集合成员,这使得成员间的误差分布特征差别很大,而集合预报是基于等概率抽样原理的,成员间差异太大并不利于构造一个可靠的集合预报系统,有必要对其进行订正。另外,在交互式全球大集合(TIGGE)等项目的推动下,各国家之间的交流更加密切,一个中心往往也能收集到其他中心的预报结果,为多模式集合预报的发展创造了条件,这也要求我们要对来自不同中心,具有不同概率分布特征的集合预报结果进行订正。因此,为提高集合预报对天气预报的指导意义,在使用集合预报结果之前进行适当的误差订正是非常必要的。
集合预报的订正主要包括两步:一阶矩系统误差的订正和二阶矩集合离散度的调整。前者目的在于调整预报PDF的中心位置以增加预报可靠性,后者是为了调整预报PDF的宽度来改善发散度不足的情况。目前,对一阶矩系统误差的订正已经比较成熟和完善,国际上对二阶矩离散度订正的研究还比较少,其原理和方法的理论基础还有待进一步的探讨和研究。其中,A drian等[1]用Bayesian Model Averaging(BMA)方法对集合预报进行订正取得了较好的效果;Gneiting等[2]用集合模式输出统计(EMOS)和最小CRPS估计的方法尝试了二阶矩离散订正;另外,Hagedom[3]等采用非齐次高斯回归(NGR)方法对E CMWF和GFS集合预报在北美地区的2m温度概率预报进行了订正研究;Jun等[4]用自适应Kalman滤波方法通过Decaying Average也能够合理地调整集合离散度的大小,明显提高了概率预报的预报能力。
1 资料介绍NMCC中尺度集合预报系统是以IBM-sp高性能计算机为运行平台,在非静力高分辨率中尺度模式WRF的基础上搭建的,模式分辨率为0.15×0.15,预报时效是36小时内每3小时间隔。本文选用NMCC中尺度集合预报系统2007年7月24日至8月24日每天12时(世界时)起报的2m温度预报结果,预报区域为30~45°N、105~125°E,以及相应区域内我国400个站1日8次的温度观测资料。为了便于预报员直接使用,并减少插值过程产生的误差,采用双线性插值法把格点预报结果插值到站点,再对站点预报进行相关研究。
作者曾对NMCC中尺度集合预报系统的2m温度预报做了一阶矩系统误差订正研究[5],检验结果表明,NMCC模式的2m温度预报存在系统误差较大、离散度不足的问题。一阶矩订正对系统误差的订正效果较好,但无法改善集合离散度不足的问题。为进一步改善集合预报效果,本文在系统误差订正的基础上进一步对NMCC模式2m温度预报做二阶矩离散度订正研究,并评价预报订正效果,特别是概率预报的订正效果。
2 二阶矩误差订正的原理和方法针对中尺度集合预报分辨率高、预报时效短的特点,本文选用了Cui Bo等提出的自适应卡尔曼滤波偏差订正方法。该方法具有以下优点:(1)方法简单,计算方便;(2)对较短时效预报的订正效果较好,能够利用较小的样本快速达到收敛,适合中尺度短期集合预报。
2.1 订正原理自适应(类卡尔曼滤波)误差订正方法通过递减平均降低误差尺度,原理是通过处理一系列带有误差的实际测量数据而得到所需要物理参数的最佳估算值。自适应算法的目的是根据滤波自身产生的预报残差、滤波残差等信息对模型进行修正,降低滤波产生的误差,以达到最佳的滤波效果。利用观测数据进行递推滤波的同时,不断地由滤波本身来判断动态系统是否有变化。如果判断发生变化并决定把这种变化作为随机干扰,则由滤波本身去估计由它产生的模型噪声方差阵[6]。或者当模型噪声方差未知或不确切时,由滤波本身不断地去估计和修正。
用自适应卡尔曼滤波方法进行二阶矩集合离散度订正,实质上就是根据集合离散度偏小(偏大)的情况不断对其进行修正。一个好的集合预报系统,离散度与均方根误差应该是相当的。因此我们以均方根误差与离散度的比值r为修正系数,对集合预报离散度进行修正。
2.2 订正步骤本文在一阶矩的系统误差订正的基础上进一步展开对二阶矩离散度的订正研究。具体步骤如下:
首先,计算集合预报在各站点i各时次t的集合平均fi(t);
其次,估算修正系数ri(t)。
| $ {r_i}\left( t \right) = rm{s_i}\left( t \right)/sprea{d_i}\left( t \right) $ | (1) |
再次,选择适当的权重系数,计算滤波后的修正系数Ri(t);
| $ {R_i}\left( t \right) = \left( {1 - w} \right){R_i}\left( {t - 1} \right) + w{r_i}\left( t \right) $ | (2) |
对Ri(t)的初始化有两种处理方法[4],一是简单地令Ri(t)在初始时刻等于零,称为冷启动;另一种方法则是以过去一段时间rmsi(t)/spreadi(t)的平均值作为Ri(t)的初值,称为热启动。为简化计算,本文对修正系数Ri(t)实行冷启动。
最后,在初始模式预报中扣除通过历史资料估算出的误差。其中
| $ Fi\left( t \right) = \overline {({f_i}\left( t \right)} - {B_i}\left( t \right)) - \left( {{f_i}\left( t \right) - \overline {{f_i}\left( t \right)} } \right) \times {R_i}\left( t \right) $ | (3) |
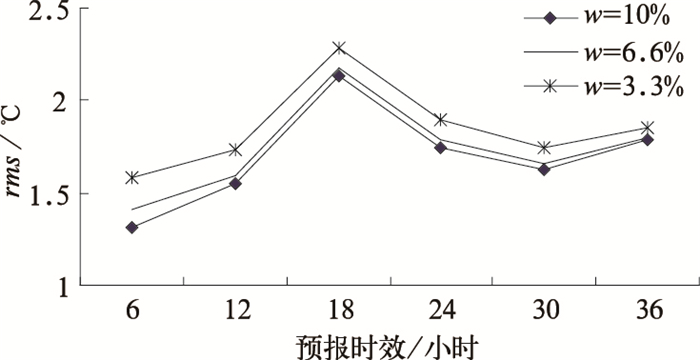
前人对全球集合预报误差订正的权重做了一定的研究。Cui Bo等[7]通过对w的一系列敏感性试验,最终选定w=2%为权重系数,相应地使用50天的历史资料;李莉[8]等则根据季节特点,夏季选取w=3.3%,使用30天的历史资料,其他季节w =1.6%,使用60天的历史资料。本研究中,鉴于区域模式预报时效短、范围小的特点,选取w=3.3%(使用30天的历史资料)、w=6.6%(使用15天的历史资料)和w =10%(使用10天的历史资料)对2m温度预报进行敏感性试验,并对8月5—24日的均方根误差平均值进行分析(图 1),结果表明w=10%时预报误差是最小的。因此,本文确定w=10%为权重系数,相应的使用过去10天左右的历史资料。
|
图 1 权重系数w的敏感性试验 |
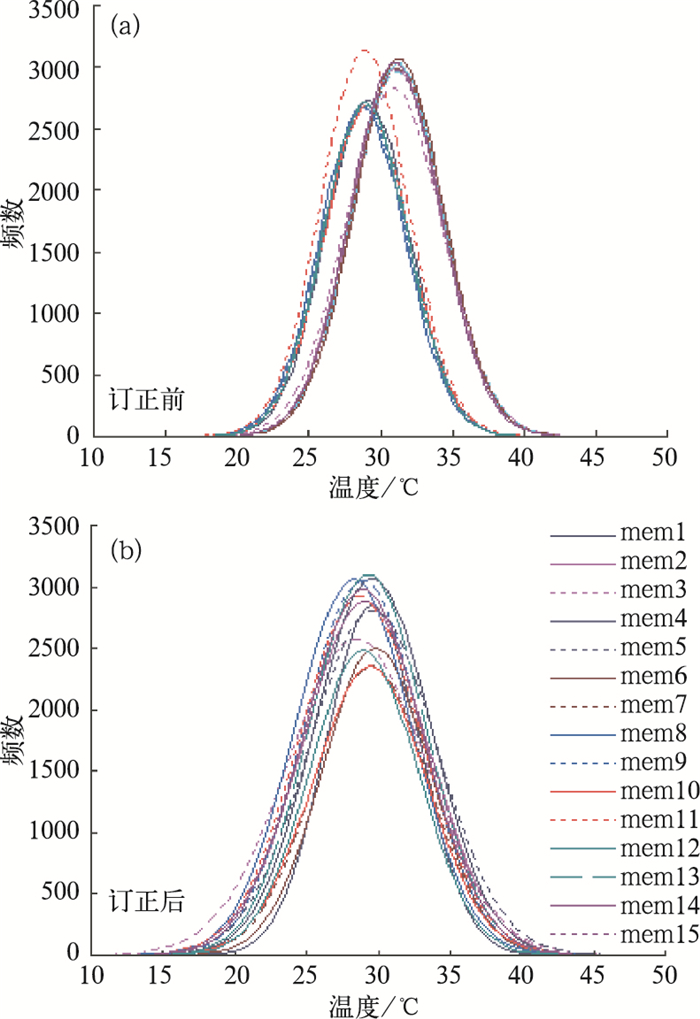
图 2给出了NMCC模式各集合成员2m温度18小时预报的PDF分布图。从图中可清晰地看到,订正前的集合成员呈现出两种形态的PDF分布形式,15个成员大致分成了两类。而集合预报的目的之一是提供预报的可靠性。如果集合预报成员间差别很大,那么很明显至少其中有些预报是错误的。订正后集合成员预报的PDF分布比较一致。
|
图 2 各集合成员18小时预报的PDF分布 |
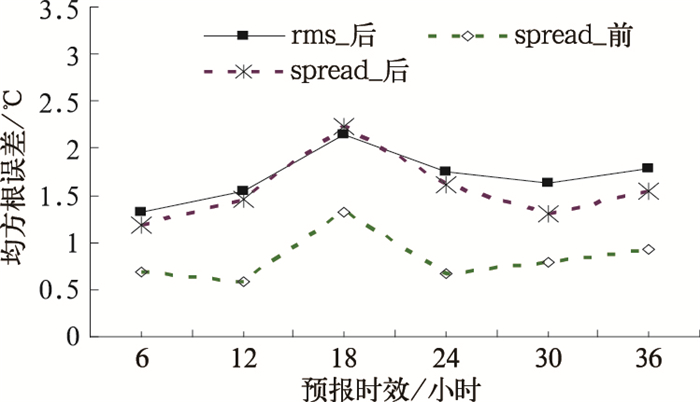
一个好的预报均方根误差和离散度应该是相当的。一阶矩订正不改变离散度,所以虽然系统误差得到改善,但集合预报仍存在离散度不足的情况。二阶矩订正后离散度得到合理的增大,与均方根误差相近(图 3),说明订正后的预报提供了未来大气的一种较好的可能性。
|
图 3 2m温度预报的均方根误差和离散度对比 |
一个好的预报系统必须满足的首要条件就是可靠性。主要针对以下两个问题展开[9]:(a)集合成员的预报结果作为预报PDF中的取样,实况检验值是否落在这个取样的范围之内?(b)温度场的预报概率与观测频率之间有何差别?根据问题的性质,对上述两个问题分别采用talagrand分布和可靠性曲线来进行分析。
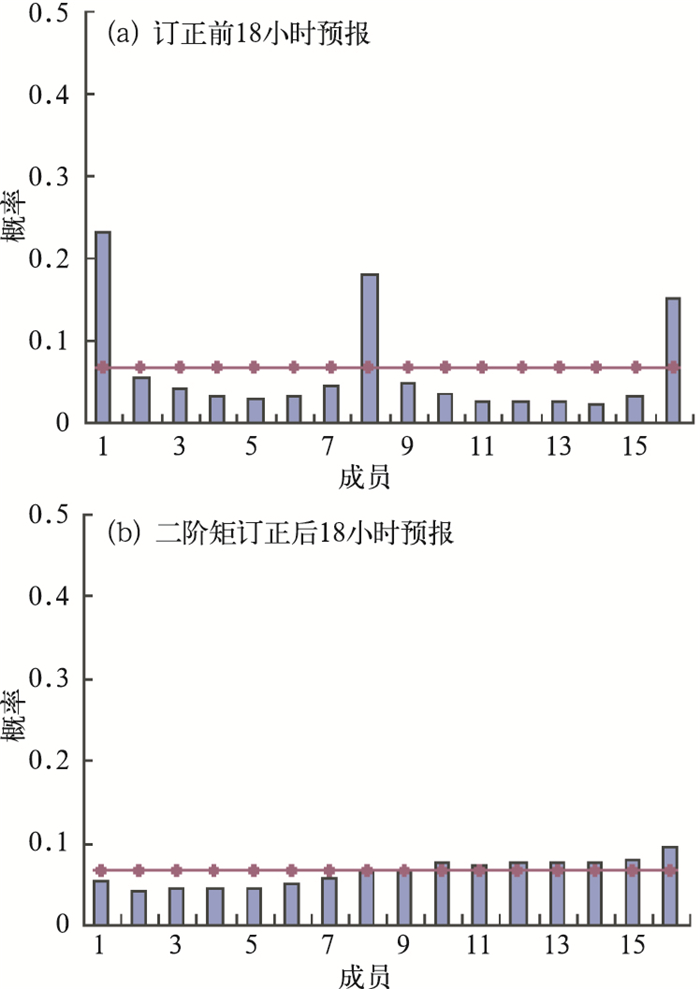
3.3.1 talagrand分布分析talagrand分布图是一种必须的检验手段,用来衡量预报值和检验值是否来自相同的概率分布[10],其形态可以反映预报系统可靠性方面的信息。根据talagrand分布的原理,理想的集合预报talagrand分布应该在所有区间一致(图中的直线),分布不均匀则表示集合平均存在误差。从集合离散度考虑,如果落在第一和最后区间的概率之和大于期望值,就说明集合成员的离散度不足,没有把实况观测值包含在预报PDF的取样空间内。图 4中,订正前talagrand分布为明显的两端高,中间低的“U”型分布,说明预报的离散度不足。二阶矩离散度订正后,talagrand分布较为均匀,与理想状态非常接近,说明此时的预报可靠性有较大提高。
|
图 4 2m温度预报的talagrand分布比较 |
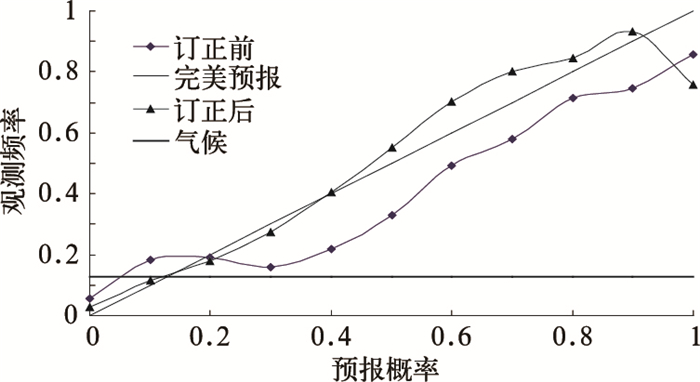
可靠性曲线(reliability diagram)[11]是通过对一段时间的预报结果和相应实况的统计,揭示预报系统对事件的预报频率与气候频率的差别。理想的可靠预报系统,预报概率与观测频率完全一致。图 5给出了2m温度18小时预报大于32℃的可靠性曲线。图中对角线表示理想状态,即完美预报——预报概率等于观测频率。由该图可看出,订正前预报的低(高)预报概率事件,其观测频率一般相对偏高(低),而订正后的可靠性曲线在大多数情况下都比较接近理想状态,预报比较可靠。
|
图 5 18小时的2m温度预报>32℃的可靠性图表 |
在上述可靠性分析的基础上,再对概率预报结果的分辨能力进行对比分析。分辨能力描述的是集合概率预报结果在与气候频率尽可能一致的前提下对具体天气事件的识别能力。
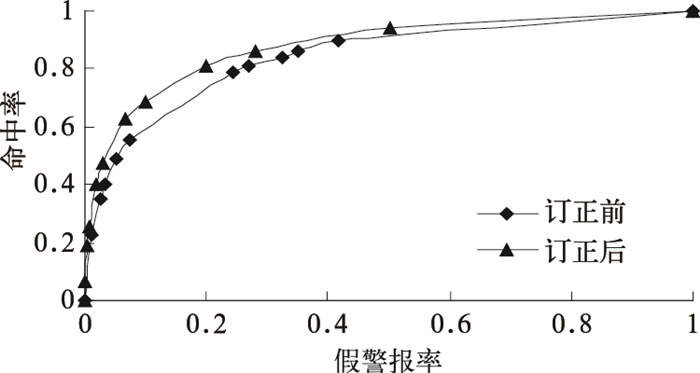
3.4.1 roc分析roc分析法是信号探测理论在数值天气预报中的一种应用[12],通过计算命中率和空报率来描述预报系统的分辨能力。由命中率、空报率在平面直角坐标系中构成一条曲线,图中的点由不同概率阈值下的命中率和空报率确定,命中率越高,空报率越低,则预报效果越好。所以roc曲线越接近图的左上方越好。左上角的点对应理想预报(所有预报都命中,命中率为1,空报率为0)。在对角线上,命中率和空报率相等,认为其预报结果与气候预测结果相当,已经不能识别具体的天气事件,对天气预报而言没有价值,如果曲线位于对角线以下,则说明其预报结果还不如气候预测。图 6中,2m温度预报的roc曲线整体包络在订正前的roc曲线之上,说明各预报概率下订正后预报的效果都优于订正前。
|
图 6 18小时的2m温度预报>32℃的roc分析 |
EV分析方法是近年来提出并广泛使用的一种方法,该方法以用户能够从天气预报中获得多大的经济效益来评价天气预报的质量。它是在ROC分析基础上的改进, 不仅考虑预报系统本身的性能(例如用ROC分析中的命中率、空报率来描述),而且还与不同类型用户对预报结果的反应有关。Richardson[13]和Mylne[14]的研究结果表明基于集合预报的概率预报远比单一的确定性预报有经济效益。
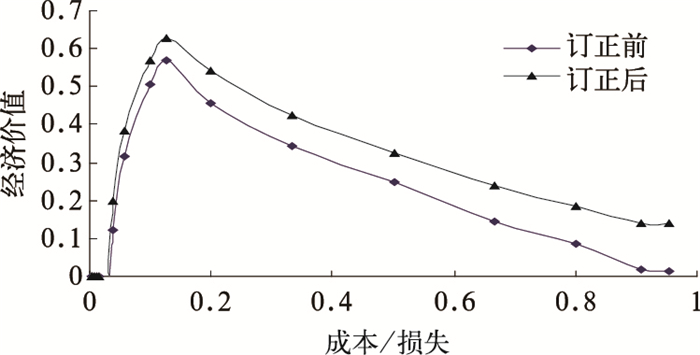
图 7是18小时预报在32℃温度阈值下的经济价值评价结果。图中横坐标为成本/损失比,表示不同类型的用户,纵坐标为经济价值。其中成本指用户对某一预报的天气事件采取防范行为所需的费用;损失指用户不采用这个预报,一旦发生这一天气事件用户会遭受到的经济损失。经济价值则是建立在气候预报和理想预报基础上的相对经济价值,而且对于集合概率预报而言,这一经济价值结果是在所有概率阈值下相对经济价值的最大值包络。所以对该用户来说如果耗费/损失比率大于1.0,他就可以不采取防范行动;反之,如小于1.0,他应该采取必要的防范措施。图中,订正后18小时预报的2m温度EV分析曲线包络在订正前的曲线之上,说明经济价值要高于订正前,这一结果与roc曲线的分析结果一致。
|
图 7 18小时的2m温度预报>32℃的EV分析 |
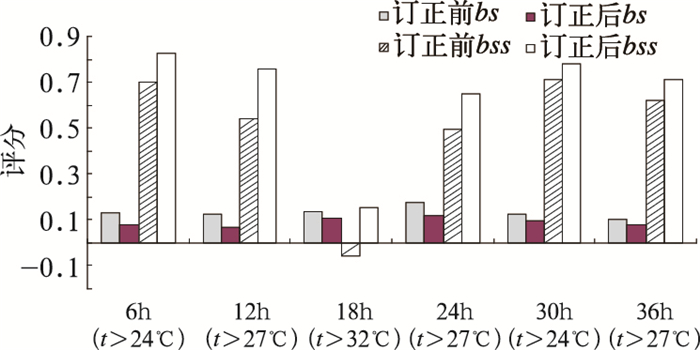
bs(brier评分)是一种均方概率误差,该方法综合考虑了可靠性、分辨能力和不确定性。bs值越小越好,bs=0表示概率预报最佳,预报正确;bs=1表示评分最差,预报失效。在bs基础上定义的bss(brier技巧评分),引入了气候bs评分,表示预报对气候预报的改进程度。与bs相反,bss越大越好,bss>0预报才有意义,反之概率预报不如气候预报[15]。图 8可以看出各时效预报在对应温度阈值下的bs评分都低于订正前,bss评分高于订正前,说明订正后预报技巧有了很大提高。
|
图 8 各时效2m温度预报的bs和bss评分 |
评估一个集合预报系统的整体性能可采用crps评分指标(continuous ranked probability score),代表观测和预报的累积分布函数(cdf)的差别[16]。
| $ {\rm{crps}} = {\rm{E}}\left[{\int {_\mathit{\Omega }{{\left( {{F_p}\left( x \right)-Fo\left( x \right)} \right)}^2}{d_x}} } \right] $ | (4) |
其中Ω是预报区域;E[·]指在所有站点和预报时期上的平均;Fp和Fo分别为预报和观测的累积分布函数。
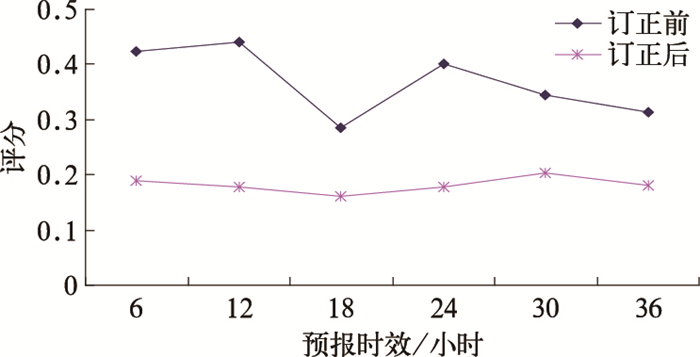
crps值越大,观测和预报的累积密度函数的差别越大,表示集合预报系统的预报能力越低。图 9中可以看到,误差订正后各时效预报的crps评分都减小了,预报能力得到提高。订正前18小时的2m温度预报crps评分在6个时效预报中最小,说明虽然由于温度日变化的影响,白天的预报误差较大,但整体上看18小时的2m温度预报能力是最高的。订正后各时效预报的crps评分比较相近,说明订正后2m温度的预报能力比较稳定。
|
图 9 各时效2m温度预报的crps评分对比 |
通过对NMCC中尺度集合预报系统2m温度预报结果的全面检验分析,评价订正前后的预报能力,得到以下几点结论:
(1) 订正后各集合成员预报的PDF比较一致。
(2) 离散度和均方根误差曲线对比可发现,二阶矩订正对2m温度预报的离散度订正效果显著。订正后预报的离散度得到合理增大,且与均方根误差较为接近,达到了调整离散度的预期效果。
(3) 针对集合概率预报可靠性的talagrand分布分析表明,二阶矩离散度订正后,talagran d分布较为均匀,与理想状态非常接近,说明此时的预报可靠性有很大提高。
(4) 针对集合概率预报分辨能力的roc分析和EV分析表明,订正后的roc曲线和EV曲线均整体包络在各自对应的订正前曲线之上,说明在各个预报概率下,订正后的2m温度预报效果都比订正前要有所改善。
(5) 概率预报评分结果分析:比较18小时概率预报的bs、bss评分结果,各温度阈值下订正后预报的bs评分都小于订正前,bss评分大于订正前,预报效果较好;订正后各预报时效的c rps值都比订正前小,预报整体性能得到提高。
(6) 文中只分析了2m温度的误差订正效果。为验证这个结果是否具有普遍意义,采用的误差订正方法对其他连续型变量是否同样适用,作者还对850hPa温度和500hPa位势高度做了二阶矩误差订正研究(略),订正效果同样显著。然而对降水等比较难把握的极端天气现象,如何进行有效的误差订正,提高降水预报能力,这更是预报员所面临并急需解决的难题。
| [1] |
Adrian E Raftery, Tilmann Gneiting. Using Bayesian Modeling Averaging to Calibrate Forecast Ensembles[J]. Monthly Weather Review, 2005, 133: 1155-1174. DOI:10.1175/MWR2906.1 |
| [2] |
Tilmann Gneiting, Adriane Raftery, Anton H, et al. Calibrated Probabilistic Forecasting Using Ensemble Model Output Statistics and Minimum CRPS Estimation[J]. Mon. Wea. Rev, 2005, 133: 1098-1118. DOI:10.1175/MWR2904.1 |
| [3] |
Hagedorn R, Hamill T, Whitaker J. Probabilistic Forecast Calibration Using ECMWF and GFS Ensemble Reforecasts. Part Ⅰ: 2-meter Temperatures[J]. Mon. Wea. Rev, 2007, 136: 2608-2619. |
| [4] |
Jun Du, Geoff DiMego, Zoltan Toth., Bias correction for the SREF at NCEP and beyond[R]. Feb. 26, 2007. A discussion at the EMC Predictability Meeting.
|
| [5] |
马清, 龚建东, 李莉, 等. 超级集合预报的误差订正与集成研究[J]. 气象, 2008, 34(3): 42-48. DOI:10.7519/j.issn.1000-0526.2008.03.007 |
| [6] |
王辉赞, 张韧, 王彦磊, 等. 基于Kalman滤波的副热带高压数值预报误差修正[J]. 热带气象学报, 2006, 22(6): 661-666. |
| [7] |
Bo Cui, Zoltan Toth, Zhu Yuejian et al. The Trade-off in Bias Correction between Using the Latest Analysis/Modeling System with a Short, vs. an Older System with a Long Archive. http://www.emc.ncep.noaa.gov/gmb/ens/papers/manuscript_thorpex_bocui.pdf
|
| [8] |
李莉, 朱跃健. T213降水预报订正系统的建立与研究[J]. 应用气象学报, 2006, 17(Suppl). |
| [9] |
段明铿. 夏季影响我国的重要中期环流过程集合预报效果研究[C]. 博士论文, 2006年5月. http://cdmd.cnki.com.cn/Article/CDMD-10300-2006066407.htm
|
| [10] |
Hou D, Kalnay E., Droegemier K, K. Objective verification of the SAMEX'98 ensemble forecasts[J]. Mon. Wea. Rev, 2001, 129: 73-91. DOI:10.1175/1520-0493(2001)129<0073:OVOTSE>2.0.CO;2 |
| [11] |
David J.Stensrud, Nusrat Yussouf. Short-range ensemble predictions of 2m temperature and dewpoint temperature over New England[J]. Monthly Weather Review, 2003, 131: 2510-2524. DOI:10.1175/1520-0493(2003)131<2510:SEPOMT>2.0.CO;2 |
| [12] |
皇甫雪官. 国家气象中心集合数值预报检验评价[J]. 应用气象学报, 2002, 13(1): 29-36. |
| [13] |
Richardson D.S. Skill and relative economic value of the ECMWF ensemble prediction system[J]. Quart. J. Roy. Meteor. Soc, 2000, 126: 649-668. DOI:10.1002/qj.v126:563 |
| [14] |
Mylne K.R., Evans R.E., Clark R.T. Multi-model multi-analysis ensemble forecasting in quasi-operational medium range forecasting, submitted to Quart[J]. J. Roy. Meteor, 2000. |
| [15] |
谭燕. 中尺度强降水天气集合预报技术的研究[D]. 硕士论文, 2006: 25. http://cdmd.cnki.com.cn/Article/CDMD-85101-2006083048.htm
|
| [16] |
Stanski H. R., L. J. Wilson and W. R. Burrows. 1989: Survey of common verification in meteorology. Geneva[R], Switzerland, World Meteorological Organization World Weather Watch Report No. 8(TD No. 358): 114.
|
 2008, Vol. 34
2008, Vol. 34