2. 桂林供电局;
3. 广西大学电气工程学院
2. Guilin Power Supply Bureau;
3. School of Electrical Engineering, Guangxi University
电力负荷预测是供电部门的重要工作之一,合理、准确地进行负荷预测可以提高电力企业的经济效益和社会效益[1]。影响负荷预测准确率的因素很多,其中气象条件是主要因素之一。长期以来,许多气象和电力专家都致力于充分利用气象因素提高电力负荷预测准确率的研究,如文献[2]综合应用人工神经网络、模糊理论等智能技术考虑天气因素对电力负荷的影响,利用陕西省9个地市1998—2001年的逐日8个气象要素以及对应的逐日电力负荷值,对陕西省电力负荷进行训练和预测,较大地提高了日负荷预测的精度。文献[3]从华中电网4省电力负荷资料中分离出随气象因子变化的气象负荷,并重点研究了气象负荷随气温变化的规律,为该地区电力部门进行负荷预测工作提供了重要的参考依据。
本文在分析了桂林地区的负荷特性以及气象特点的基础上,利用2005年和2006年逐日(不包括五一、十一、春节等节假日)的负荷与气象资料分离出了受气象条件影响的气象负荷,并研究了气象负荷与各气象因素之间的相关关系。最后利用这些气象因素建立了一种基于相似日的气象负荷预测方法,同目前使用较多的回归方法[4-5]相比,能较好地反映天气变化对气象负荷的影响。
1 气象负荷的提取一般来说,负荷的变化受到多种因素的制约,而且这些因素对负荷变化的影响程度又互不相同,再加上负荷具有一定的随机性,因此准确地对负荷进行分离是一项复杂而又困难的工作。通过参考相关文献气象负荷的提取方法,将整个原始负荷分解成长期增长趋势项(简称经济负荷)、由气象因素引起变化的负荷(简称气象负荷)、随机因素引起变化的负荷(简称随机负荷),具体定义如下[6-7]:
| $ L = {L_t} + {L_m} + \varepsilon $ | (1) |
这里L表示原始负荷,Lt表示负荷的长期增长趋势项,Lm表示气象负荷,ε表示各种随机因素引起的负荷变化。由于ε变化比较复杂,难以用具体式子表示,从负荷的长期演化趋势来看对整个负荷贡献相对较小,因此本文暂不考虑。长期增长趋势项是用线性回归来表示对负荷发展的长期趋势项Lt的拟合:
| $ {L_t} = a + bt $ | (2) |
其中,Lt为负荷发展的长期趋势项,a、b为系数,t为时间。本文采用最小二乘法估计系数a、b,从而得到参数a、b的估计值为:
| $ \begin{array}{l} \widehat a = \frac{1}{n}\sum\limits_{i = 1}^n {{L_i}-\widehat b} \frac{1}{n}\sum\limits_{i = 1}^n {{t_i}} \\ \widehat b = \frac{{n\sum\limits_{i = 1}^n {{t_i}{L_i}-(\sum\limits_{i = 1}^n {{t_i}} )(\sum\limits_{i = 1}^n {{L_i}} )} }}{{n\sum\limits_{i = 1}^n {t_i^2-{{(\sum\limits_{i = 1}^n {{t_i}} )}^2}} }} \end{array} $ | (3) |
这样,根据Lm=L-Lt即实际负荷与长期增长趋势项的偏差就可分离出气象负荷。
2 气象负荷与各气象因素的相关分析不同地区因其地理位置、气象特点、负荷构成等原因的不同,各气象条件对负荷的影响程度也不尽相同,因此如何根据各地区不同的特点来分析电力负荷与气象因素之间的相关关系,对指导本地区供电部门的负荷预测工作具有重要意义。本文主要针对桂林地区的气象负荷与各气象因素进行了相关分析。
2.1 气象负荷与温度的相关分析所利用的历史资料为桂林地区2005年、2006年的日负荷以及逐日的气象资料,因为在五一、十一、春节等节假日的负荷比较特殊,所以实际利用的数据是去除这些特殊日剩余的数据,所用的数据样本满足Pearson相关系数检验的要求。同时为了分析方便,在作图分析时分别将负荷、气象数值归一化为0到1之间,具体公式为
| $ x' = \frac{{x-{x_{\min }}}}{{{x_{\max }}-{x_{\min }}}} $ | (4) |
其中x为某个负荷或气象值,xmax、xmin分别为该数据的最大、最小值,x′为归一化后的值。
对该地区全年各月气温与气象负荷的相关系数进行分析,如表 1所示(该表仅为平均气温与最大气象负荷的相关系数分析结果,其与最小气象负荷、平均气象负荷的相关系数亦有类似结果,因篇幅关系本文未列出)。从12月到次年3月,气温与气象负荷呈负相关的关系,从4月到11月,气温与气象负荷是正相关的关系。根据这一特点,将全年分为冬夏两个季节分别进行研究,其中冬季在本文指12月到次年的3月,夏季指4月到11月。冬季气温与气象负荷相关系数为负值,说明在冬季气象负荷随温度的升高而减小,而相关系数较小是因为地处亚热带地区的桂林冬季相对温暖,取暖负荷较小,其气象负荷也相对较小,气温对负荷的影响不大。夏季气温与气象负荷呈现出正相关,说明在夏季,气温的升高会导致气象负荷增大,这是由于气温升高时制冷负荷增加引起的,此外,从表 1的数据还可以看出,日平均气温与气象负荷相关系数较大的月份集中在5—9月。这是因为,桂林的5—9月比较炎热,再加上桂林是全国著名的旅游城市,宾馆、休闲场所较多,人们会频繁使用空调、风扇等降温设备,导致制冷负荷较大。因此夏季的这几个月内气象负荷与气温的相关系数较大,这些数据可为建立季节性负荷模型提供依据。据统计,2005年、2006年夏季5月到9月共计153天中,大于等于30℃的天数分别为112天、103天,分别占总天数的73.2%、67.4%;大于等于34℃的天数分别为47天、37天,分别占总天数的30.72%、24.18%。
|
|
表 1 2005、2006年平均气温与桂林电网最大气象负荷的相关系数 |
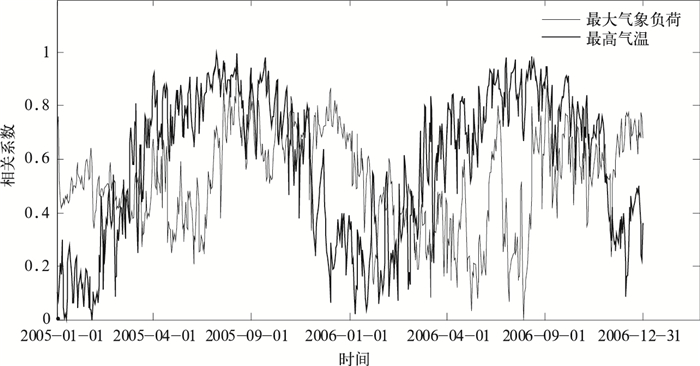
由于桂林地区夏季持续的时间比较长,气候比较炎热,经常出现持续数天高温的情况而导致整个电网负荷波动比较大,对电网负荷预测带来了极大的影响。图 1是经归一化处理后最高气温与最大气象负荷的关系曲线图。从该图可以看出,夏季6月到9月上旬气温升高时,气象负荷会有明显的增长,而9月中旬到11月气温降低时,气象负荷会回落,原因是9月中旬以后,高温天气逐渐减少,天气逐渐转凉。进一步分析发现,全年日气象负荷的峰值主要集中在8、9月份,因为这两个月在桂林地区高温少雨,酷热干燥,特别是持续数天的高温天气会给桂林带来一段时间的峰值负荷,这是季节性的气候造成的。2005年全年气象负荷的最大值出现在8月12日,这一天的最高气温达到了37.6℃,而这一温度也是2005年整个年度的最高温度;2006年全年气象负荷的最大值出现在9月3日,这一天的最高气温达到了36℃,而整个2006年度只有6天高温天气超过了36℃。根据上述分析可见,夏季的高温天气预报对电网负荷预测具有较好的指导意义。
|
图 1 2005、2006年最高气温与最大气象负荷关系曲线 |
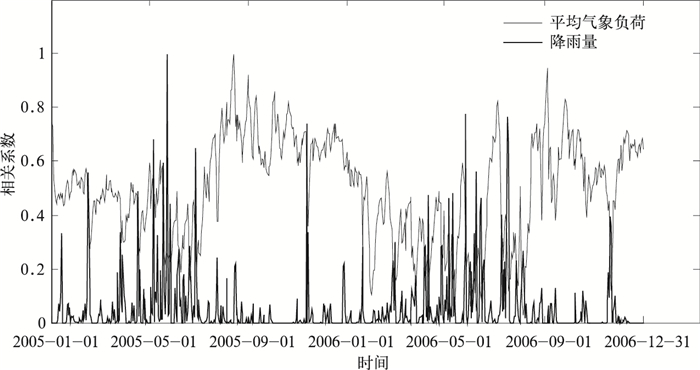
广西降雨丰富,在分布上形成三个多雨区和两个少雨区。三个多雨区是:一是十万大山东南侧的东兴至钦州一带;二是大瑶山东侧以昭平为中心的金秀、蒙山一带;三是越城岭至大苗山东南以永福为中心的兴安、灵川、桂林、融安、融水一带。这三个多雨区中心,年降水量均在2000mm以上。桂林地区恰属多雨地带,降雨因子对气象负荷的影响也较大。图 2是2 005、2006年降雨量与平均气象负荷关系曲线,由图可知,较大的降雨会导致气象负荷的明显下降。2005年降雨主要集中在5、6月份,共有40天降雨,其中小雨为17天,中雨10天,大雨8天,暴雨3天,暴雨量级以上为2天,在5、6月份平均气象负荷明显降低;2006年降雨主要集中在4月1日至5月13日、5月24日至6月18日、7月6日至7月18日,共降雨62天,其中小雨33天,中雨9天,大雨14天,暴雨5天,暴雨量级以上1天,在降雨比较多的这些天内平均气象负荷有不同程度的降低,而5月14日至5月23日、6月19日至7月5日均无较大降雨,再加上此时气温比较高,因此气象负荷又有明显的回升。通过分析发现,小雨时气象负荷变化并不显著,难以进行统计分析,当降雨量级为中雨时,其平均气象负荷下降幅度约3%~10%;大雨时下降幅度约5%~15%;暴雨时下降约10%~20%;暴雨量级以上时平均气象负荷下降的幅度将更大,例如2005年6月5日降雨量级达到了大暴雨级,其平均气象负荷下降了约25%。研究中还发现,某日较大的降雨,不仅会影响到该日的负荷,还会影响到后续几日的负荷,即降雨的影响时间长。值得注意的是,目前该地区的气象部门只能提供整日的降雨量预报,也就是用一天降雨量的总值来反映全天各个时刻的降雨变化情况,若能将全天分成几个时段,然后分别提供各个时段的降雨信息,这将对短期负荷预测工作带来更大的实际参考价值。
|
图 2 2005、2006年降雨量与平均气象负荷关系曲线 |
一般认为,人体对大气环境的反应可以大体表现为温度、湿度和风力的综合影响,基于此,人们提出了“人体舒适度”这一概念。所谓“人体舒适度”就是指在不特意采取任何防寒保暖或防暑降温措施的前提下,人们在自然环境中是否感到舒适及其达到怎样一种程度的具体描述[8]。各地因气候条件的差异采用的舒适度指数计算公式并不相同,广西采用的公式为
| $ DI = 1.8T-0.55(1.8T-26) \times (1-RH) - 3.2\sqrt V + 32 $ | (5) |
其中,DI、T、RH、V分别代表舒适度指数、温度(℃)、相对湿度(用小数表示)、风速(m·s-1)。
通常人的皮肤温度比身体温度略低一些,大约是32℃。从理论上讲,当气温高于32℃时人体就应该产生炎热的感觉,可事实并非如此。例如, 在气温35℃的环境中, 若空气的相对湿度在40%~55%, 平均风速在3m·s-1以上, 人们就不会感到很热,但若湿度增大到70%以上,风速很小时,就会产生闷热难熬的感觉,导致出现中暑现象。所以,人们对环境温度的感觉是受诸多因素综合影响的[9]。为了表示出舒适度指数对负荷的影响程度,本文对2005、2006两年各月舒适度指数与气象负荷的相关系数进行分析,发现对于地处亚热带地区的桂林,夏季(5—9月)舒适度指数与最大、平均气象负荷的相关系数较好,这与上文中对气温与气象负荷的关系是一致的。具体相关系数值如表 2所示(由于篇幅关系,本文仅列出5—9月舒适度指数与平均气象负荷的相关系数),此外,舒适度指数与气象负荷的相关系数普遍高于温度、湿度、风力与气象负荷的相关系数。这是因为舒适度指数是温度、湿度、风力等气象特征值的综合表现,第三产业用电及居民生活用电所占比例较大的桂林负荷对其变化更为敏感。因此,在实际负荷预测建模中,可用舒适度指数代替其它气象因子作为负荷预测的综合变量,以此来提高预测的准确率。
|
|
表 2 舒适度指数与平均气象负荷的相关系数 |
根据上述分析,当计算出相应的气象负荷Lm后,再加上负荷的长期趋势项Lt即可得到整个的电力负荷。本文尝试采用一种相似日的预测方法来计算气象负荷。相似日方法的基本思想是首先将影响电力系统日负荷的各因素构成一个日特征向量,用以描述该日的特征,然后采取某种相似评估分析方法根据日特征向量的相近程度从历史日中选取若干相似日,再根据预测日和相似日的数据进行下一步计算[10]。本文采用灰色关联分析法来选取历史的相似日,具体方法如下:
设x0,xi分别为预测日及历史日各影响因素构成的向量,i=1, 2…l,则有
| $ \begin{array}{l} {\mathit{\boldsymbol{x}}_0} = [{\mathit{x}_0}(1), {\mathit{x}_0}(2), \cdots {x_0}(\mathit{n})]\\ {\mathit{\boldsymbol{x}}_i} = [{\mathit{x}_i}(1), {\mathit{x}_i}(2), \cdots {x_i}(n)]\\ 称\\ {\zeta _i}(\mathit{k}) = \frac{{\mathop {\min }\limits_i \mathop {\min }\limits_k \left| {{\Delta _i}(k)} \right| + \rho \mathop {\max }\limits_i \mathop {\max }\limits_k \left| {{\Delta _i}(\mathit{k})} \right|}}{{\left| {{\Delta _i}(\mathit{k})} \right| + \rho \mathop {\max }\limits_i \mathop {\max }\limits_k \left| {{\Delta _i}(\mathit{k})} \right|}} \end{array} $ | (6) |
为x0与xi在第k点的关联系数。在上面式子中,Δi(k)=x0(k)-xi(k),ρ为分辨系数,是0到1之间的数,一般取ρ=0.5。综合各点的关联系数,可得出整个x0与xi的关联程度ri为
| $ {r_i} = \frac{1}{n}\sum\limits_{k = 1}^n {{\zeta _i}(\mathit{k})} $ | (7) |
本文的日特征向量由星期类型、最高温度、最低温度、降雨、人体舒适度指数构成,按照上述公式选取与预测日特征向量相近即关联度比较大的若干历史日作为相似日,则预测日的气象负荷可由相似日的气象负荷进行加权得到
| $ L{'_m} = {k_1}{L_{m1}} + {k_2}{L_{m2}} + \cdots + {k_p}{L_{mp}} $ | (8) |
式中,L′m为预测日的气象负荷,Lm1, Lm2,…Lmp为所选的p个相似日各日的气象负荷,ki为权系数,i=1, 2, …p则由各相似日的关联度大小来确定:
| $ {k_i} = \frac{{{r_i}}}{{\sum\limits_{j = 1}^p {{r_j}} }}, i, j = 1, 2, \cdots p $ | (9) |
求出气象负荷之后,再根据Lt=a+bt计算出负荷长期趋势项Lt,即可确定预测日总的电力负荷。
应用上述计算负荷的方法对桂林地区2005年12月1日到12月21日共3周的日最大负荷、日最小负荷、日平均负荷进行计算分析,得到预测日最大负荷的平均相对误差为3.6%,预测日最小负荷的平均相对误差为4.06%,预测日平均负荷的平均相对误差为2.72%,由此可见,采用该方法对桂林地区的日负荷预测取得了比较满意的效果。
4 结束语气象因素是影响电力系统负荷的重要因素,研究气象与负荷的关系对当地电力部门的负荷预测工作具有重要意义。通过分析桂林地区2005、2006年的气象与负荷资料,从原始负荷中分离出了气象负荷,并着重分析了桂林地区气象负荷与各种气象因素之间的相关关系,针对桂林地区的负荷特性和气象特点得出了一些重要的结论。对于气象负荷的预测,建立了一种基于相似日的日负荷预测方法,通过实际的算例验证,取得了比较满意的预测效果。同时也应该注意到,负荷预测的准确率受到诸多因素的影响,因此在进行实际的负荷预测时还要综合考虑其它的影响因素以及预测人员的经验,这样才能得到更加合理的结果。
| [1] |
牛东晓, 曹树华, 赵磊, 等. 电力负荷预测技术及其应用[M]. 北京: 中国电力出版社, 1998.
|
| [2] |
罗慧, 巢清尘, 李奇, 等. 气象要素在电力负荷预测中的应用[J]. 气象, 2005, 31(6): 15-18. DOI:10.7519/j.issn.1000-0526.2005.06.003 |
| [3] |
胡江林, 陈正洪, 洪斌, 等. 华中电网日负荷与气象因子的关系[J]. 气象, 2002, 28(3): 14-18. DOI:10.7519/j.issn.1000-0526.2002.03.003 |
| [4] |
孙东霞, 杨建成. 克拉玛依电网电力负荷与气象条件关系的研究[J]. 新疆气象, 2002, 25(6): 9-11. |
| [5] |
林小红, 夏丽花, 黄美金, 等. 福州市夏季电力气象等级预测模型初探[J]. 气象科技, 2006, 34(6): 774-777. |
| [6] |
张远亲, 房云龙, 汤燕冰. 浦东电力负荷特性及与气象条件关系的研究[J]. 科技通报, 2006, 22(1): 21-27. |
| [7] |
陆建宇, 王亮, 王强, 等. 华东电网气象负荷特性分析[J]. 华东电力, 2006, 34(11): 38-42. DOI:10.3969/j.issn.1001-9529.2006.11.011 |
| [8] |
周巍, 陈秋红, 肖晶, 等. 人体舒适度指数对用电负荷的影响[J]. 电力需求侧管理, 2004, 6(3): 54-56. |
| [9] |
秦海超, 王玮, 周晖. 人体舒适度在短期电力负荷预测中的应用[J]. 电力学报, 2006, 21(2): 143-145. |
| [10] |
钱卫华, 姚建刚, 龙立波, 等. 基于负荷特性分析的短期负荷预测相似日选择方法[J]. 华中电力, 2007, 20(1): 17-21. |
 2008, Vol. 34
2008, Vol. 34