2. 北京市气象局;
3. 青岛市气象局;
4. 山西省雷电监测防护中心
2. Beijing Meteorological Bureau;
3. Qingdao Meteorological Office;
4. Shanxi Provincial Lightning Protecting Centre
科学定量地评估奥运演练期间及2008北京奥运气象服务所产生的社会经济效益,是奥运气象服务的一项重要工作。本文将北京奥组委、奥帆委等体育官员定位为奥运气象服务高端用户群,认为对其期望度和满意度的测量可以作为衡量奥运气象服务社会经济效益的标准之一。综合应用AHP法和BCG矩阵方法,将这些高端用户群对奥运气象服务效益评估这个复杂系统的思维过程数学化、系统化。并以2007年青岛国际帆船赛现场的调查问卷作为实证分析依据,根据用户需求的了解和满足、气象服务的时间和时效、气象服务的宣传服务手段、服务人员综合能力、预报准确度和用户未来意向等多重指标体系,来衡量用户群对气象信息服务的期望度和满意度,定量评估当前奥运气象信息服务的结构现状和存在问题,继而改进和提高。
1 社会经济效益评估方法——期望度/满意度组合矩阵模型的提出 1.1 层次分析法(AHP法)层次分析法(The Analytic Hierarchy Process,简写AHP)是1970年代由美国学者Saaty提出,是解决多目标评价决策问题的一种定性和定量相结合的有效方法。其特点是将决策人对复杂系统的思维过程数学化、系统化,以便使决策依据易于被人接受。同时,应用AHP方法使所需的定量信息要求不多,但可以把握决策人对决策问题的本质、所包含的系统要素及其互相之间的逻辑关系;此外,AHP法对无结构化的系统的评价决策及多目标决策问题很适用[1]。
AHP法的基本思路是决策人通过将复杂问题分解为若干层次,每一层次又有若干要素组成,然后对同一层次各要素以上一层次的要素为准则进行两两比较、判断和计算,以获得各要素的权重,从而为选择最优方案提供决策依据。其中,AHP法最关键的是建立判断矩阵,即以上一层的某一要素EH作为判断准则,对下一层要素进行两两比较来确定矩阵的元素值,也是进行各要素优先级权重计算的重要依据。
1.2 波士顿咨询集团矩阵(BCG矩阵)波士顿咨询集团矩阵(Boston Consulting Group Matrix,简称BCG矩阵)是流行于欧美大型企业的一种新型战略分析与决策技术,因发明者美国波士顿咨询集团而得名。其目的在于分析企业内各业务分部在市场竞争与产业发展中的相对优势,并据此制定企业各分部的结构性经营与发展战略[2]。处于BCG矩阵各象限的业务分部之间存在相互转换和相互作用的关系,各分类分部角色的相互转化一般取决于两方面因素,一是决策者能否顺应产品生命周期和市场需求要求的变化而调整其业务组合,二是各业务分部能否在市场竞争中取胜进而增强自己的市场地位。即使非常成功的业务单位也有一个生命周期,它们从问题业务开始,继而成为明星业务,然后成为现金牛业务,最后变成瘦狗业务而至生命周期的终点。正是如此,决策者不仅要考察其各项业务在矩阵中的现有位置,还要以运动的观点看问题,观察其未来可能的发展趋向,不断检查其动态位置[3]。
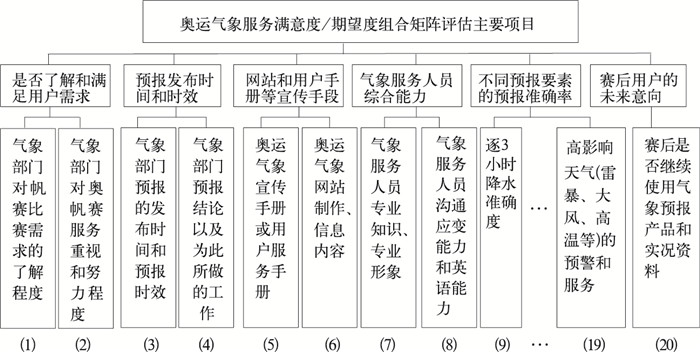
1.3 气象期望度/满意度组合矩阵分析模型的思路本文认为可以借助层次分析法的处理和波士顿矩阵分析相结合的思路对奥运气象信息服务社会经济效益进行分析,以形成较为客观的期望度指数和满意度指数来取代波士顿矩阵中传统的市场占有率和销售增长率,从而建立气象期望度/满意度组合矩阵分析模型,期望度和满意度恰当结合,可以发现问题,促进气象部门尽快采取改进措施[4]。图 1显示了该组合矩阵评估项目的独立性结构。
|
图 1 组合矩阵评估主要项目的独立性结构 |
下文将具体阐述所提出的期望度/满意度组合矩阵模型的步骤,以2007年青岛国际帆船赛现场调查问卷作为实证分析的依据,根据气象产品特性(准确性、及时性等)、服务时间和效率、服务人员能力和态度、未来意向和整体的表现等多重指标体系来衡量用户群对气象信息服务的期望度和满意度,定量评估当前奥运气象信息服务的结构现状和存在问题。
2 气象期望度/满意度组合矩阵分析模型的步骤气象期望度/满意度组合矩阵分析模型是将期望度和满意度恰当结合,气象信息服务期望度(重要度)表示用户对气象部门服务的期望程度,代表了来自用户群的需求引力,主要表现为满足需求提供的机会或施加的限制;满意度是指气象部门所提供的气象信息被用户实际感受,所产生的满意程度,表示了供给的动力,主要表现内外环境交互作用的综合结果,可以通过气象部门的努力和调整得到加强和提高。
奥运气象服务中考核项目的期望度和满意度大小可分别表示为:
| $ {X_i} = {A_i} \times {W_i} $ | (1) |
| $ {Y_i} = {B_i} \times {W_i} $ | (2) |
其中:Xi为主项满意度计算值;Yi为主项期望度计算值;Ai为主项满意度评价值,按强弱从1~7的正整数取值(分析值);Bi为期望度评价值,按高低从1~7的正整数取值(分析值);Wi为主项重要性评价值,通过AHP方法取得(计算)[5]。具体计算步骤如下。
(1) 首先根据所获得的奥运气象服务调查问卷,其中每类数据应用不同的基础指标,期望度和满意度得分都用加权平均的方法获得。比如,将其中20个基础指标满意度进行综合归类、整理成为6类气象信息服务属性,新的满意度得分都用加权平均的方法获得,它们分别是:将问卷中的基础指标1.1~1.2归类为综合指标01,代表是否了解和满足用户需求;将1.3~1.5、1.20归类为综合指标02,代表预报发布时间和时效;将1.6~1.8归类为综合指标03,代表服务手册和网站等服务和宣传服务手段;将1.9~1.10归类为综合指标04,代表服务人员能力;将1.11~1.17归类为综合指标05,代表针对不同预报要素的预报准确率;将1.18~1.19归类为综合指标06,作为用户的未来意向,即是否在赛后继续使用气象预报产品和实况资料。
奥运气象满意度要素的综合分析,在专家调查的基础上得出是否了解和满足需求、预报发布时间和时效、网站和用户手册等宣传服务手段、服务人员能力、不同预报要素的预报准确度和用户的未来意向等6项的满意度综合评价值为:
| $ A = \left( {4.73, 4.47, 4.3, 4.33, 3.88, 3.90} \right) $ |
奥运气象期望值的综合分析,得出是否了解和满足需求、预报发布时间和时效、网站和用户手册等宣传服务手段、服务人员能力、不同预报要素的预报准确度和用户的未来意向等6项的期望度综合评价量化值如下:
| $ B = \left( {3.7, 3.4, 3.2, 3.73, 3.06, 3.53} \right) $ |
(2) 接着建立判断矩阵,作为AHP法的基本信息,也是进行各要素优先级权重计算的重要依据。判断矩阵是以上一层的某一要素EH作为判断准则,对下一层要素进行两两比较来确定矩阵的元素值。以EH为判断准则的有n阶的判断矩阵。判断矩阵A中的元素aij表示从判断准则EH角度考虑要素Ai对要素Aj的相对重要性,表 1所示就是常见的判断尺度,表示要素Ai对要素Aj相对重要性的数量尺度。本文采用1~7级判断尺度计算要素Ai对于上一级要素EH的相对重要度,四个数字分别表示1:同样重要;3:稍微重要;5:明显重要;7:强烈重要。如当Ai比Aj重要,则aij=Wi/Wj, 反之若Aj比Ai重要,则aji=1/aij,以此类推。
|
|
表 1 判断尺度表 |
(3) 采用专家调查的方法,确定各主项的排序矩阵。求出判断矩阵的特征向量W,然后经过归一化处理,即可求出Ai关于EH的相对重要度(权重)。特征向量分量Wi可用
再对W=(W1, W2, ...Wn)T进行归一化处理:
(4) 由于决策者或者专家认识的多样性和客观事物的复杂性,各决策者对决策对象有不同的偏好,从而给出的决策判断矩阵,并不能与实际相吻合得很好,因此,有必要对AHP进行一致性检验和必要的校正。运用方根法计算判断矩阵的最大特征值及对应的特征向量得出其每个项目的权重评价数据Wi及相容性指标C.I.。如果有关相容性检验指标均小于0.1,则相对重要度的计算值可以接受。
在对系统各要素的重要性程度进行两两比较的判断时,一般不可能完全精确地判断出Wi/Wj的比值Wi/Wj,只能对它进行大致的估计,如果在估计时有误差,必然会导致判断矩阵特征值也有偏差。若判断矩阵A被判断为A′,这里表示有偏差矩阵存在,则A′被称为不相容判断矩阵,就有:
| $ A'W' = {\lambda _{\max }}W' $ |
式中,W′表示带有偏差的相对重要度向量。若与矩阵A完全相容时,则有最大特征值λmax=n,当稍有不相容时,则λmax>n。设度量相容性的指标为C.I.,则:
| $ C.I. = \frac{{{\lambda _{\max }} - n}}{{n - 1}} $ |
在问卷中专门设计有针对女垒赛期间服务质量属性的相对重要性进行打分评判的内容,分别对应6个主要项目。本文共有15个体育专家参与打分,包括奥组委体育官员、国内外领队、裁判、外国帆船队的随队气象水文专家等,其中1位专家的打分值和C.I.计算如表 2。
|
|
表 2 对奥运气象服务主要项目相对重要度的判断矩阵(专家1) |
通过表 2得到:Wio=(0.4198, 0.193, 0.193, 0.079, 0.079, 0.036), λ=(6.24,6.11,6.11,6.06,6.06,6.27),算得C.I.≤0.10,可以认为判断矩阵A′有相容性,据此而计算的Wio值是可以接受的[1]。
(5) 本文共有15组专家参与评判,涉及北京奥组委官员、国际垒联ISF裁判长、女垒场馆经理等,对评判得出的相对重要评价值加权平均,其中有13组为通过相容性检验的可使用数据,将这13组Win加权平均,得出6个主要项目的权重W为:
| $ \begin{gathered} W = \left( {0.183, 0.137, 0.151, } \right. \hfill \\ \;\;\;\;\;\;\;\;0.210, 0.122, \left. {0.220} \right) \hfill \\ \end{gathered} $ |
(6) 根据计算得出的Wi及分析得出的Ai、Bi,算出Xi与Yi的数据,分别将其作为平面坐标的横轴与纵轴坐标值,绘制该项目在图中的位置。
3 气象期望度/满意度组合矩阵模型的分析结果由式(1)和(2)得出奥运气象信息服务产业化中是否了解和满足需求、预报发布时间和时效、网站和用户手册等宣传服务手段、服务人员能力、不同预报要素的预报准确度和用户的未来意向等6项的满意度及期望度分别为:
| $ \begin{gathered} X = \left( {0.866, 0.611, 0.648, } \right. \hfill \\ \;\;\;\;\;\;\;\;0.911, 0.492, \left. {0.860} \right) \hfill \\ Y = \left( {0.677, 0.465, 0.482, } \right. \hfill \\ \;\;\;\;\;\;\;0.785, 0.389, \left. {0.779} \right) \hfill \\ \end{gathered} $ |
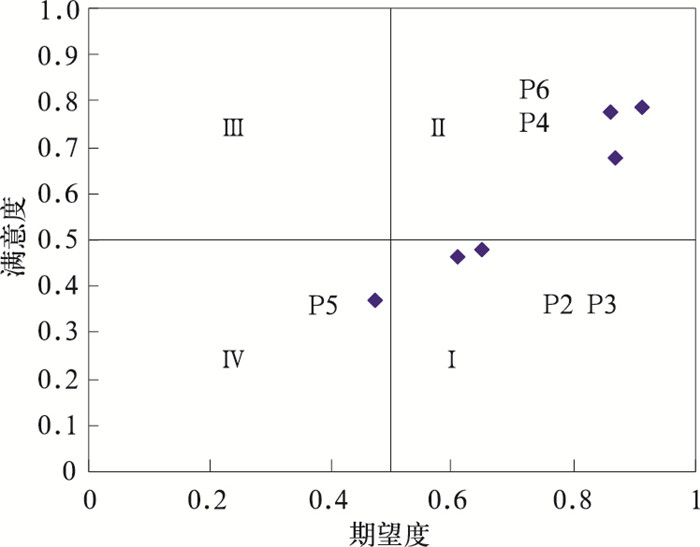
各项目的满意度和期望度的组合(Xi, Yi), i=1, 6,与各项目期望度/满意度相对应的坐标位置Pi(Xi, Yi),即对用户需求的了解和满足P1(0.866,0.677)、气象服务时间时效P2(0.611,0.465)、气象服务宣传手段及内容P3(0.648,0.482)、服务人员综合能力P4(0.911,0.785)、预报准确率P5(0.473,0.373)、用户未来意向P6(0.860,0.779),决定了该项在满意度/期望度框图中处于不同的区域,为了便于做出分析,将整个区域划分成4个象限。
考虑到气象信息过程中不可避免的风险因素及服务项目分类可能存在的差异以及需要改进的可能性,将四个象限的分界线定在中心位置,如图 1。将4个象限分别命名为:Ⅰ、培育类项目,Ⅱ、收获类项目,Ⅲ、成功类项目,Ⅳ、改革类项目。
|
图 2 奥运气象服务满意度与期望度组合矩阵模型 |
依据以上分析结果,得到以下相关结论以及建议对策:
第一,气象服务宣传手段及内容P3和气象服务时间时效P2均处在第一象限,是需要进一步培育的项目,说明仍然蕴藏着发展潜力。
奥运气象网站、奥运气象宣传手册或用户服务指南等宣传和服务手段非常重要。通过互联网形成自己的“窗口"媒体是奥运期间气象信息服务主战场。但目前奥运气象网站的内容还不够充分;用户反馈在2007年奥帆赛时,还应提供气象服务中英文手册或用户服务指南等(前年曾经发放过),并建议在服务手册最后几页,能增加气象常识,比如:等压线,副热带高压等的介绍。在未来不到一年的时间里,网站需要制作还得再专业、信息再丰富些,还需要广为宣传、努力提高点击率。奥运期间对气象服务时间时效要求更加苛刻,同时预报的时效要求更高。
第二,对用户需求的了解和满足P1、服务人员综合能力P4以及用户未来意向P6目前处在第二象限,属于收获类项目,标志着该项目相对成熟,已经成为气象部门产生社会经济效益的项目,并将成长为重要支柱项目之一。
在未来不到两年的时间里,还需要从用户的角度了解、归类和挖掘需求,甚至可以引导和帮助用户发现气象与体育赛事之间的需求;了解到需求,才可以针对需求进一步提高服务的时间和时效;对于是否了解和满足用户的需求,这从用户的角度客观地反映出,在挖掘用户需求面还需要下力气。比如,奥帆委用户更为关注小尺度天气预报,尤其是风要素预报,不太关注大尺度的形势预报,对于气象部门现在所提供的未来一周展望觉得对比赛的指导意义不大。另外,还认为细分用户非常重要,比如针对渔民、爬山类用户等,应该提供分门别类的气象信息服务。说明在未来不到一年的时间里,还需要从用户的角度了解、归类和挖掘需求,甚至可以引导和帮助用户挖掘需求。
奥运气象服务队伍是一支很重要的队伍,直接面对用户、服务公众,这支队伍人员的遴选范围在奥运筹备和实战期间已经扩展到全国气象部门,统一配置人力资源。他们需要懂预报、善沟通、英语强,要承担奥组委和奥运赛场的预报预警信息的解释应用,及时与用户沟通交流并向本部反馈用户意向,在这些体育官员面临社会压力时、帮助他们一起完成与天气事件相关的决策,并完成奥运服务社会经济效益评估工作。这些工作直接关系奥运气象服务的成败,也直接会影响这些目标用户未来使用气象信息的意向。因此,在现有基础上继续提高服务人员综合能力,现场服务人员不断提高英文水平、交流和应变能力都是需要继续努力的方向。
对于此次赛事完毕后,是否继续使用气象数据或者气象信息的未来意向评价最高,用户希望竞赛海域各浮标站资料加密更新,希望能看到实时雷达资料,并在测试赛以后,还希望继续在网站上发布相关观测资料。
第三,目前还没有相关项目落在第三象限,即成功类,说明未来不到两年时间气象部门仍然需要继续努力,促使收获类项目成为成功类,促使培育类项目向收获类转化。
第四,预报准确率P5落在第四象限,即改革类项目,提醒提高天气预报准确率是做好气象服务工作的重中之重。
如何提高天气预报准确率属于老调长谈,同时是做好气象服务工作的首要前提和重中之重,每前进一步都要付出很大的努力,但这又是气象部门的立业之本,始终需要气象人长抓不懈。前几届成功的夏季奥运会经验告诉我们,及时高效跟进的气象服务可以有效弥补气象预报不准确带来的负面效应。提高天气预报准确度在国际帆船赛期间的气象要素预报中,裁判和领队认为对于3m·s-1以上的风向以及风向的转向更为重要,可以据此确定不同的航线,风速小则航线短,风速大则航线较长。要彻底解决预报“不准”的问题,来自用户的建议中有以下几点:(1)参加航海运动,提高临场经验,比如对现场气象服务人员进行帆船赛的海上短期培训;(2)在帆船赛中多到海上体验;(3)需要对航海运动所需要的、依赖的微观气象领域加强分析、判断等。
综合上述,气象部门决策者可以通过气象满意度/期望度四象限矩阵法的分析,运用定量和定性相结合的综合分析,通过用户反馈来评估当前奥运气象信息服务的几个主要项目的结构现状,掌握其所处位置并预测该项目的未来发展变化,发现问题进而改进,进一步有效合理分配气象经营资源。
| [1] |
汪应洛. 系统工程[M]. 北京: 机械工业出版社, 1999: 190-198.
|
| [2] |
陈捷. 波士顿咨询集团矩阵功能及原理简析[J]. 数量经济技术经济研究, 1999(12): 36-38. |
| [3] |
哈罗德孔茨, 海因茨韦里克. 管理学(第9版)[M]. 北京: 经济科学出版社, 1998: 112-114.
|
| [4] |
罗慧, 万迪昉, 魏明. 气象信息服务产业化战略杠杆与核心能力组合分析[J]. 经济问题探索, 2003(5): 112-116. |
| [5] |
Milind M.Lele. Creating Strategic Leverage: Matching Company Strengths with Market Opportunities[M]. New York: John Wiley & Sons, 1992: 30-90.
|
 2008, Vol. 34
2008, Vol. 34