地面粗糙度是指空气动力学粗糙度Z0,是风速等于零的某一几何高度, 它表征地表与大气的相互作用,反映地表对风速的减弱作用,是大气边界层理论研究的一个重要参数[1]。在超声风速仪问世前,确定地表空气动力学粗糙度的传统方法通常是利用测量得到3层以上的中性风廓线外推或非中性层结廓线迭代求最佳拟合解[2],近年来的另一种方法是利用一高度超声风温仪的湍流测量资料确定地表粗糙度的方案,张宏□等[3](1997)介绍了一种利用单一高度风速、温度湍流资料确定空气动力学参数的方法,该方法无须进行风速廓线的测量,可以应用于非单一水平均匀下垫面和非中性层结。高志求等[4](2002)利用北京气象塔大气湍流观测资料, 由单层超声风速、温度资料估算非均匀下垫面空气动力学参数的方法,计算了中国科学院大气物理研究所气象塔附近的下垫面空气动力粗糙度。李倩等[5](2003)利用梯度观测方法和粗糙元分析方法计算了北京325m气象塔周围粗糙度的变化。虽然用梯度观测的方法在实际应用中会有一定困难,如真正的中性层结资料很难获得,高质量风廓线的测量困难和实施风速梯度观测的不便等,但用此方法来估算空气动力学粗糙度仍是目前常用的基本方法之一。
天津255m气象塔是研究城市边界层的理想观测平台,刘学军等(1991)[6]曾利用1988年气象塔资料针对天津城市建筑群对近地层风速廓线的影响作了统计分析,发现不同性质下垫面上近地层的平均风速廓线存在的显著差异。刘学军等[7](1991)利用塔层20、30、40、60m的观测值按对数律拟合计算出不同方位的Z0值,赵鸣等[8](1996)利用塔层资料得到天津250米以下边界层中风切变的若干特征。本文首先利用风速梯度资料拟合对数风速廓线的方法,定量计算天津255m气象塔空气动力学粗糙度随下垫面的改变情况;其次利用近地层风的变化研究下垫面改变对城市冠层厚度的影响。
1 天津255m气象塔及观测资料图 1(见彩页)是根据1993年和2006年TM影像得到的天津市下垫面情况,其中圆圈标注位置是铁塔观测站。图中显示2003年铁塔观测站还属于市郊下垫面,随着天津市城市建设及城市化规模的快速发展,2006年该区域已经发展成为建筑物较多且分布不均匀的市区下垫面,该时段内铁塔观测资料可以反映城市下垫面改变对近地层气象特征参数的影响。本文采用的资料是1996—2005年气象塔梯度观测资料(高度分别为5、10、20、30、40、60、80、100、120、140、160、180、200、220、250m)。
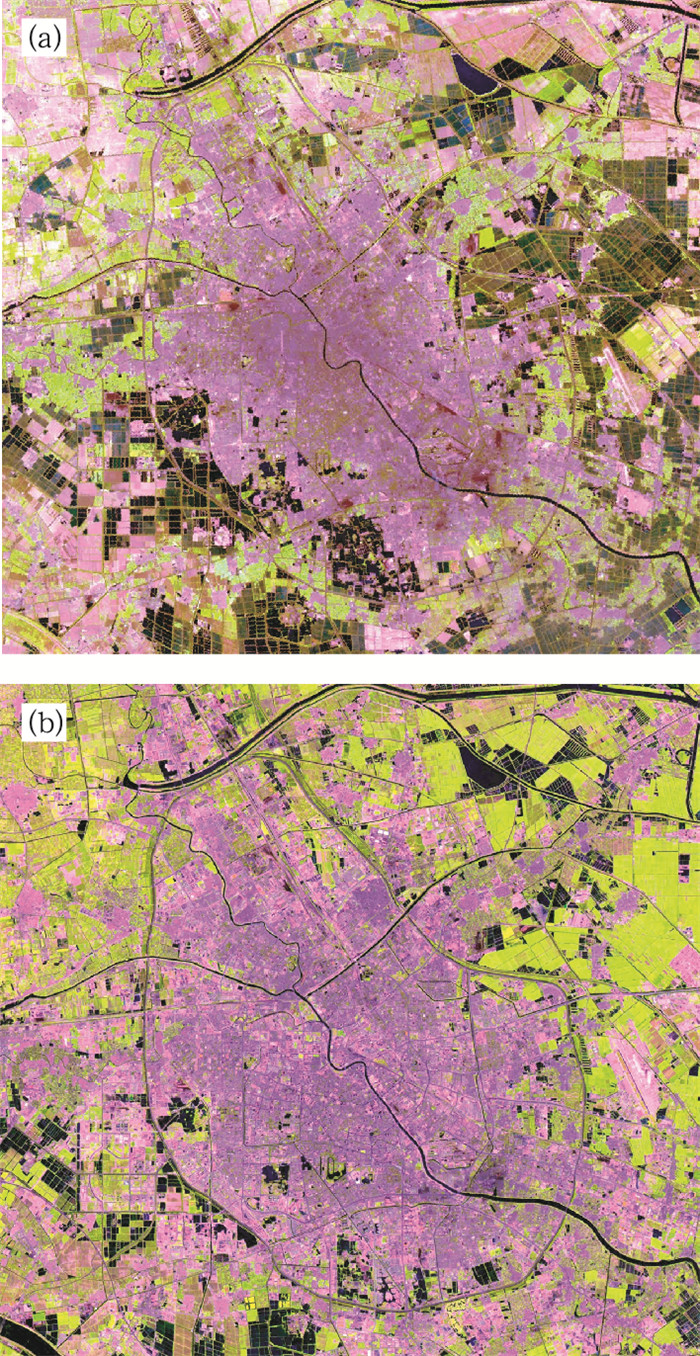
|
图 1 天津铁塔站周边地区下垫面变化情况 (a)1993年;(b)2006年 |
对实际观测的资料进行质量控制是进行理论分析的必要前提,其遵循的基本原则是最大限度保持资料的原有状态,对出现问题的资料进行合理的校正和订正。在这个过程中,要求所进行的工作不影响整个资料的物理意义。首先分析不符合一般统计特征的温度和风速资料,将有问题的资料剔除,由于资料量大,剔除处理需要自动进行,采用的剔除原则是:对于风资料,由于探测采用三杯风速计,最小启动风速为0.5m·s-1,20米以上层次的观测风速小于该值时,判断为错误值剔除,同时风速梯度为零的廓线资料也予剔除;在处理风向资料时,由于风向变化的随机性很大,很难找到合适的诊断与订正原则,且在对订正资料做平均时,风向资料的处理中存在一个“过零问题”。在这种情况下,采用气象上常用的“最大频率风向法”,即把风向从0~360°划分为16个方向,然后取频率最大的平均风向为实际风向。
2 天津255m气象塔空气动力学粗糙度利用风速梯度资料拟合对数风速廓线的方法,定量计算天津255m气象塔空气动力学粗糙度随下垫面的改变情况。根据莫宁-奥布霍夫相似理论,中性层结近地面层水平风速分布满足对数律[9],即:
| $ u = \frac{{{u^ * }}}{k}\ln \frac{{z - d}}{{{z_0}}} $ | (1) |
其中,u为风速,u*为近地面摩擦速度,κ为von Karman常数,Z为离地面的实际高度,Z0为地面粗糙度,d为零平面位移。考虑铁塔周围以主要建筑是6层居民楼,d取值为15m。1996—2005年期间共有78449组有效廓线资料,本文采用梯度理查逊数Ri对近地层特征进行分类,考虑铁塔周围建筑物影响,计算时采用20m和60m两层的温度和风速实测值,Ri计算公式如下:
| $ {R_{\text{i}}} = \frac{g}{{{T_0}}}\left[ {\frac{{\Delta T}}{{\sqrt {{z_1}{z_2}} \ln \frac{{{z_2}}}{{{z_1}}}}} + {r_d}} \right] \times \left[ {\frac{{\sqrt {{z_1}{z_2}} \ln \frac{{{z_2}}}{{{z_1}}}}}{{\Delta u}}} \right] $ | (2) |
其中:
| $ \frac{{{u_i}}}{{{u_1}}} = \ln \frac{{{z_i}}}{{{z_0}}}/\ln \frac{{{z_1}}}{{{z_0}}} $ | (3) |
| $ {z_0} = \exp \left( {\frac{{{u_1}\ln {z_i} - {u_i}\ln {z_1}}}{{{u_1} - {u_i}}}} \right) $ | (4) |
下标1、i为选择计算的层次,u为风速,z为高度,本文取20、30、40、60米的观测值进行计算。表 1给出了在N、E、NE、SE、S、SW、W和NW共8个方位平均地面粗糙度随年份的变化,可以看出:由于偏北方向对应城市建筑群,而偏南方向对应郊区的开阔地,故偏北方向的粗糙度大于偏南方向;城市化的发展使气象塔从市郊下垫面逐渐变成典型的城市下垫面,空气动力学粗糙度总体呈逐年递增的趋势,其中N、E、SE、S方向在1999—2003年增幅较大,SW和NW方向在1996—1999年增幅较大,2003年在W方向有个极小值,主要与当年城市改造有关。
|
|
表 1 各方位动力粗糙度 |
为了定量描述粗糙度和建筑物高度之间的关系,本文统计不同方位建筑群的平均高度(H)并建立统计方程如下:
| $ {z_0} = 0.063566 + 0.093813H $ | (5) |
图 2为1995年和2004年冬季不同高度风玫瑰图,对于高空风基本上是偏北风,只是不同年份所占比例有所不同,这取决于当年的大气环流及其与热岛环流的配合,与下垫面关系不大。近地层受粗糙下垫面影响风向分布紊乱,1995年主要影响到20~30m,在30米以上各风向频次开始一致,2005年则影响到30~40m,40m以上各层次风向频次基本一致。说明近十年间随着城市化发展,受下垫面影响城市冠层厚度增加10m,与前面分析的粗糙度增加的结论一致。
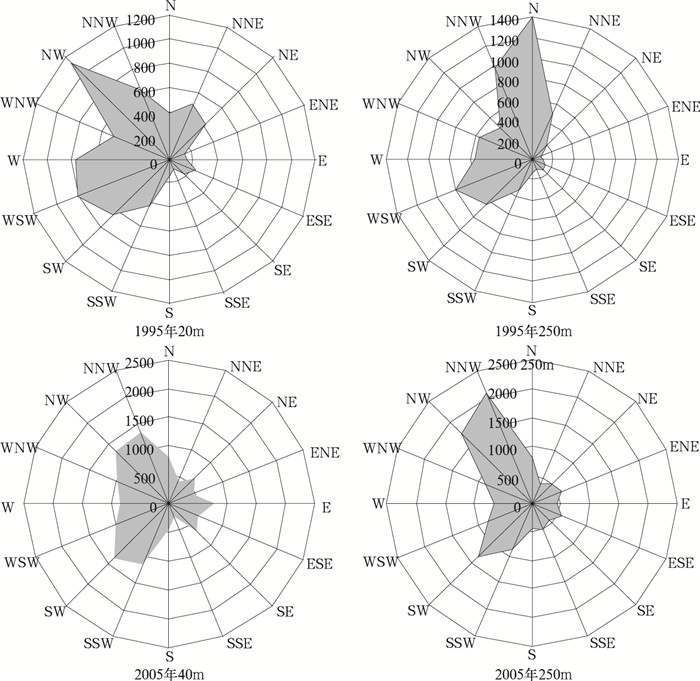
|
图 2 1995和2005年冬季不同高度风玫瑰图 |
本文以12、1、2三个月平均代表冬季风速,其中2000年和2002年的160~220m资料观测质量不好没有加入计算。表 3为天津气象铁塔冬季不同高度上平均风速的逐年变化。分析铁塔近地面各层的风速发现,受城市下垫面的影响,近地面的平均风速有逐年递减的趋势,且高度越低的层,平均风速逐年递减的趋势也越为显著,2005年城市冠层厚度在40~60m之间。
|
|
表 3 天津气象铁塔不同高度冬季风速随年代变化(m·s-1) |
(1) 利用风速梯度资料拟合对数风速廓线的方法,定量计算天津255m气象塔空气动力学粗糙度随下垫面的改变情况,偏北方向的粗糙度大于偏南方向;空气动力学粗糙度总体呈逐年递增的趋势,个别年代减小与城市改造有关,粗糙度与城市建筑群高度之间存在线性关系。
(2) 冬季风速资料表明城市化进程对边界层风场结构产生了显著的影响,近地面风向逐年趋于紊乱,1995年主要影响到20~30m,2005年则影响到30~40m,说明近十年间随着城市化发展,受下垫面影响城市冠层厚度增加10m。
(3) 受下垫面影响平均风速呈现非常明显的逐年递减的趋势,而且越靠近地面,平均风速逐年递减的趋势也越为显著,2005年城市冠层厚度在40~60m之间。
| [1] |
刘小平, 董治宝. 空气动力学粗糙度的物理与实践意义[J]. 中国沙漠, 2003, 23(4): 337-346. |
| [2] |
阵家宜, 王舟民, 光田宁. 一种确定地表蛆糙度的独立方法[J]. 大气科学, 1993, 17(1): 21-26. |
| [3] |
张宏, 阵家宜. 非单一水平均匀下垫面空气动力学参数的确定[J]. 应用气象学报, 1997, 8(3): 310-315. |
| [4] |
高志球, 卞林根, 逯昌贵, 等. 城市下垫面空气动力学参数的估算[J]. 应用气象学报, 2002, 13(Suppl): 26-33. |
| [5] |
李倩, 刘辉志, 胡非, 等. 城市下垫面空气动力学参数的确定[J]. 气候与环境研究, 2003, 8(4): 443-450. |
| [6] |
刘学军, 吴丹朱. 城市建筑群对低层大气风速廓线影响的统计分析[J]. 气象, 1991, 17(7): 14-18. DOI:10.7519/j.issn.1000-0526.1991.07.003 |
| [7] |
刘学军, 吴丹朱, 马富春. 天津市250m低层大气风廓线模式的试验研究[J]. 大气科学, 1991, 15(5): 33-39. |
| [8] |
赵鸣, 唐有华, 刘学军. 天津塔层风切变的研究[J]. 气象, 1996, 22(1): 7-12. DOI:10.7519/j.issn.1000-0526.1996.01.002 |
| [9] |
苗曼倩, 赵鸣, 王彦昌, 等. 近地层湍流通量计算及几种气象塔风廓线模式的研究[J]. 大气科学, 1987, 11(4): 420-429. |
 2008, Vol. 34
2008, Vol. 34