2. 国家气象中心;
3. 河北省气象局
2. National Meteorological Center;
3. Hebei Meteorological Bureau
面雨量是在一定面积上或流域内的平均降水量,是水文气象中一个重要的参考量。作为水文模式的初值,面雨量估算值的准确与否不仅关系到水库流量以及洪水预测的准确性,还关系到流域内水库的设计与计划、水资源平衡分析、地下水补给评估、城市排水系统的设计和气候状况估计等等。
面雨量估算技术研究已经有一百多年的历史,世界上很多国家都将面雨量实时估算与预报作为日常业务之一。1998年夏季长江流域和嫩江松花江流域发生特大洪涝灾害期间,为适应国家水文部门需求,中央气象台开始进行面雨量估算和预报服务。2001年起中国气象局确定将全国七大江河流域86个子流域的面雨量实时估算与预报作为全国气象部门的日常业务之一[1]。由于降水的时空分布不均匀,如何准确估算面雨量始终是一个科学难题。随着气象学、数学、水文学、遥感等学科技术的发展,流域面雨量的估算技术也有了长足的发展,特别是卫星、雷达估测降水等非常规资料和高密度自动气象站降水资料的结合应用,已成为面雨量估算技术主要趋势。近年来,我国面雨量估算技术的研究也迅速加强,特别是随着卫星估测降水资料的日益丰富,在应用卫星估测降水资料来估算面雨量方面取得了不少成果[2-8]。但从总体来看,研究的深度和创新不足,尤其是综合运用常规和非常规资料估算面雨量的技术还很不成熟。本文拟就面雨量估算技术的国内外研究进展和发展趋势作简要综述,供相关科研和业务人员参考。
1 流域面雨量概念通常,人们把雨量计在某个特定地点所测得的降落到地面的降水量称作点雨量。但事实上,严格意义上的点雨量是不存在的,雨量计所测得的仍然是雨量筒截水面积上的平均水量。只是相对于降雨过程的空间尺度而言,雨量筒截水面积完全可以忽略不计,因而可以把测量结果看作点雨量。气象部门观测和预报的一般是作为站点位置函数的点雨量,而水文部门需要的则是流域范围内的面雨量。过去的做法是直接用点雨量来代表面雨量。由于降雨在水平方向上的高度不均匀性,点雨量并不能准确代表流域范围内的降水情况。如何通过观测到的点雨量来准确估算流域的平均降水量,就构成了流域面雨量估算的核心问题。
流域面雨量P可以通过点雨量来计算,可表示为:
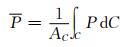
|
(1) |
其中P是作为连续函数的点雨量,C是某一特定流域,AC为流域面积。
由于降雨观测站的离散性,不可能获得完全连续的点雨量场P。实际计算是通过将式(1)离散化来完成的,即先将流域C划分为N个包含一个雨量观测的小区域,用第i个小区域上的点雨量Pi代表小区域的平均降水量,流域的面雨量则可用下式来近似计算:
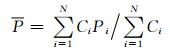
|
(2) |
一般来说,小区域面积越小,点雨量的代表性越好,计算出的面雨量越趋近于式(1)计算的结果。如果观测站点分布均匀,点雨量代表的区域面积相同,此时,面雨量就简化为点雨量的简单算术平均。可见,当只有常规观测资料可供利用时,面雨量的计算可转化为等面积栅格代表雨量估算问题,而栅格代表雨量主要通过空间插值来估算,如何提高插值的性能成为问题的关键。
近年来,雷达、卫星等非常规观测资料广泛应用于估算降水,这类降水资料与站点观测降水不同,其最终产品是像素化的降水场。相对于雷达、卫星监测范围的尺度(100km以上)而言,每个像素(如1km2上的平均降水量)仍可看作点雨量。对此较高的空间分辨率资料,可通过算术平均直接计算流域的面雨量。问题的核心则归结为如何改善雷达、卫星资料反演降水的效果。
流域的空间尺度可从几十到上千公里不等,相应的降水系统为中尺度系统到天气尺度系统。时间尺度上,从水文部门的需求角度来讲,应为日及日以下时间分辨率的降水观测。因此,流域面雨量的估算主要是针对天气尺度范围内,高时间分辨率的降水资料进行的。
2 利用常规资料(雨量计)估算面雨量由于地面气象站的空间分布不均匀,人们发展出了多种针对站点降水观测资料的空间插值方法来估算面雨量。简单的插值方法只根据待插值点(栅格中心)相对样本点(站点)的位置和样本值(雨量观测)来计算,复杂的函数插值方法和统计插值方法还可以将高程、地形等影响降雨的因素考虑进来,以改善插值效果。
用雨量计等常规方法测得的降水来估算面雨量,除了算法本身的局限性之外,其误差来源主要有两个:(1)系统误差,主要由漂移和蒸发造成,误差大小与测量时的气象条件以及仪器本身的性能有关;(2)采样误差,主要由于观测网密度低或测站布局不合理,使得观测数据的空间代表性差而造成。系统误差比较难于掌握和估计,采样误差则可用统计方法来估计,并通过增加仪器数量、优化布局来减小。
2.1 加权平均法加权平均法是将待插值点的雨量表示为样本点上雨量观测值的线性组合的一类方法,其中样本点按某种标准被赋予一定的权重。权重大多取为与插值点到样本点的距离反相关的形式。Thiessen多边形法[9]、反距离平方加权法[10]是这类方法中简单易行、广为应用的两种。尽管其对降雨场的前提假设过于简化,但由于直观简单,计算量小,可自动化运行,目前仍广泛应用在气象、水文业务中。
为了得到更好的插值效果,也可以采用迭代算法进行连续校正,每一步先用插值得到的格点场来反算样本点的雨量,其与观测值的误差再用来校正格点场的插值。气象业务中常用的Barnes客观分析[11]经过一到两步,Cressman客观分析[12]经过多步连续校正后,得到最终的插值雨量场。
反距离加权法刻画了一个相对平滑的数学曲面,对连续变量插值效果较好,但对于像降水这样分布不均匀的变量场往往会低估局地强降水,而在没有降水的地方反倒插值出降水,有时还会得到负值降水。
2.2 (平滑)函数插值方法函数插值是通过构造光滑的数学函数来拟合样本值,得到空间连续的物理量场,从而在任意点上插值的方法,如果将站点观测值看作“信号+噪音”,则希望将噪音滤去,得到信号的连续表示,亦即通过构造数学函数来对降雨观测值进行平滑,得到空间连续的降水场,从而在任意点上插值。在气象中得到广泛应用的薄板平滑样条插值[13-14]和最优插值[15]都属于用平滑函数进行插值的方法。这类方法除了用站点坐标之外,还可以将高程、地形等影响降雨分布的因素考虑进来。最优插值还可用于资料同化,融合常规和非常规观测资料进行流域面雨量估算。
2.3 地理统计方法地理统计方法[16-17]根据按空间位置(不规则)分布的观测资料,建立恰当的随机过程模型,从而做出有效合理的统计推论。地理统计要解决的主要问题之一就是根据随机变量在区域中n个位置上的观测,来估算该区域中任意一点的变量值,因此可用于空间插值。
地理统计预测又称克里金(Kriging),属于空间自相关模型,模型中只包含自身的特征值和地理位置。但由于降水与地理、气象等多种要素的空间分布具有一定的相关性,从中可以认识降水的潜在空间特征。由此产生了多变量的克里金方法,即协同克里金(cokriging)。该方法进一步假设空间分析要素与多种地理要素的分布具有内在关联性,又可以称为空间异相关模型。协同克里金应用于面雨量估算时,其最大的特点是可以在降雨的空间统计预报模型中纳入可影响天气系统的预报因子,如地形、风向等[18],以提高降水空间插值的精度。
地理统计方法估算效果较好,适合于研究应用,但因其算法复杂,且需要人工干预,不适合于自动化的业务运行。
3 利用非常规资料(卫星、雷达)估算面雨量的进展近年来,雷达、卫星等新观测手段越来越多地应用于降水监测和预报。雷达、卫星估测降水的基本原理,都是根据云团对电磁波的反射特征来推算云团的可降水量。由于电磁波的空间连续性,用雷达、卫星可估算出高空间分辨率的降水场,这是传统的雨量计观测所无法比拟的。但由于雷达、卫星是通过间接方式估算降水的,按一定的关系式换算的结果与雨量计观测相比往往有较大的出入,因此还需要与传统的常规观测相结合,经过校正后才能成为符合实际情况的估计降水产品。具体做法可将雷达、卫星估计降水与地面雨量观测资料进行融合,得到时空连续的雨量分析场[19]。比较而言,卫星适合于大范围降水场的估计,而雷达则适合于中小流域。
3.1 雷达估计降水用于面雨量计算雷达估计降水的方法主要是将雷达的回波强度Z通过一个经验关系转化为雷达降水估计R,可用下式表示:
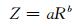
|
(3) |
其中a、b为系数。雷达估计降水的最主要不确定性来源于雷达测到的是降雨云的垂直相态,而与地面降水观测并不等价。其次,静态的Z-R关系是假设在静态大气状况下成立的,对于上升和下曳气流明显的对流性降水就不适用[20]。最后,即使是在同一雷达覆盖区域,对不同仰角和距离的回波,Z-R关系也是有所变化的[21]。
由于地面降水观测能够提供较为准确的点雨量,而雷达观测能反映降水的空间分布,若能将两者有效地结合起来,则可以得到高时空分辨率的降水场,并直接用于流域面雨量估算。对于100~10000km2的中小流域来说,洪水对降水的响应时间只有1~3小时,将实时雷达观测资料估算的面雨量应用于水文模型,进行洪水预报是相当有效的[22]。
国内外在雷达资料与地面观测相结合估算降水场方面进行了大量的工作。由英国自然环境研究委员会(NERC)主持的水文雷达实验项目(HYREX)是这一领域的开拓性研究计划之一[23]。最近完成的欧洲21个国家参加的COST 717计划主要目的是研究如何将雷达观测用于水文和数值预报模式[24]。
雷达估计降水与雨量计观测资料进行融合的较直接的方法,就是将雨量计降水和对应位置的雷达像素反演降水的比率拟合成曲面,利用此曲面来修正整个雷达反演的降水场[25]。地理统计中的协同克里金是融合雷达估计降水和雨量计观测资料的另一常用方法[26]。此外还有其它各种模型,如考虑了降水的持续性,又可实时校正雷达估计降水应用的卡尔曼滤波模型[27],应用回归方法(包括一般线性回归、岭回归和稳健回归)的统计模型[28]并基于GIS开发的业务系统[29],以及针对所研究流域只被部分雨区覆盖时估算降水场的多变量统计模型[30]等等。
3.2 卫星估计降水资料用于面雨量计算卫星估计降水是通过气象卫星传感器对云顶亮温等云团和大气辐射特征的观测结果所作的降水估计。卫星可以提供大范围、高时空分辨率的降水场估计,大大弥补了高原、海洋等地区常规雨量观测资料不足及雷达覆盖范围小的局限性。
由于卫星估计降水是像素化的图像,因此原则上可直接用于面雨量的估算。但由于卫星对雨区识别的准确性较高,而对降水量估计的准确性较低,在用于面雨量估算时,一般需要经过地面观测资料订正或融合。在高原、海洋等地面雨量观测不足的地区,单纯用雨量观测修正也有困难。这时就有必要借助其它来源的资料,如数值预报产品作为第一猜测场,来进行资料融合。Grimes等[31]采用协同克里金方法结合卫星和地面观测资料进行面雨量计算;王登炎等[3]用变分法结合卫星估计降水和数值预报产品进行面雨量预报;师春香等[32]用人工神经网络方法,徐晶和毕宝贵[8]用最优化方法,刘洪鹏和刘文[33]用反距离权重法,潘永地和姚益平[7]则利用气象卫星水汽通道资料修正地面观测资料的插值结果,再计算流域面雨量,以及直接利用卫星估计降水产品估算面雨量[2]的尝试,等等。这些工作为卫星估计降水资料用于面雨量的估算提供了多种行之有效的方法。
卫星估计降水监测范围较广,而地面雷达估计降水准确性较高。将两者的优势结合起来,联合卫星和雷达可对大流域的面雨量进行估算。例如我国“八五”期间所构建的利用雷达网和卫星联合估算长江流域大范围降水的LARORAS系统[34],对防汛抗洪和大型水库工程建设具有重大应用价值;阿迈德·迪狄安·迪阿罗等[35]联合卫星和雷达重构淮河流域大范围的降水场,用精度更高的雷达估计降水来订正卫星估计降水,所得结果的精度高于单独使用卫星估算结果的精度;基于CINRAD和卫星的淮河流域致洪暴雨综合定量估测及预警系统[36],在2003年淮河流域洪灾期间气象服务中取得明显效果。
随着遥感技术和计算技术的发展,综合运用地面气象站(特别是自动气象站)降水观测和卫星、雷达估测降水资料进行快速同化、融合得出降水场已成为可能,这方面的研究越来越受到重视,具有广阔的业务应用前景。
4 各种方法的比较和效果检验检验面雨量准确与否的关键是将什么作为面雨量的真值。目前国内外的面雨量检验比较方法主要分为三种。比较常见的是利用常规雨量站观测和雷达估计降水建立雨量插值模型,然后将未参与建模的加密站点的观测作为真值与该点的插值结果进行比较来检验。与这种方法类似的就是交叉检验的方法,即去掉一个观测点作为检验点,用其余观测点来建模,并在检验点插值,与该点的观测进行比较;然后再去掉另一个点进行比较,依此类推;最后计算所有比较点的均方根误差作为这种计算方法的定量化评定。
方慈安等[3]比较了Thiessen多边形法、Cressman客观分析以及算术平均法等对5个小流域面雨量的计算结果,认为几种方法的计算结果均无显著差异,但不同方法所得面雨量的逐日差异有的还是相当明显的。Goovaert[37]通过对葡萄牙的一个5000km2的流域分别使用单变量插值方法(Thiessen多边形法、距离平方反比法)和以及多变量地理统计方法(区域平均的克里金、引入趋势项的克里金以及协同克里金)来估算区域气候平均面雨量,在后三种方法中考虑了地形高度的影响。结果表明,前两种方法由于没有考虑地形高度及周围站点的影响,误差较大,而在对三种多变量地理统计方法的比较发现对于该流域具有外部趋势项的克里金方法具有最好的估算效果。类似的方法比较研究国际上还有很多,例如ardo-Iguzqiza[38]对西班牙南部的Guadalhorce流域利用Thiessen多边形法、普通克里金、带趋势项的克里金以及协同克里金估算流域面雨量,结果表明在考虑地形高度因子的情况下的带趋势项的克里金较其他几种方法更具有优势。
另外一种验证面雨量准确性的方法是将计算结果提供给水文模型,并将模型计算径流结果与实况观测比较。刘晓阳等[39]利用水文模型比较了分别用雷达估计降水资料和用雨量站资料做初值,结果表明利用雷达估计降水资料计算出的径流量准确性大为提高。
由于流域面雨量是推导量,缺乏来自实况观测值的直接验证,关于流域面雨量计算的检验以及各种计算方法的比较是个难题。直接对各种方法的计算结果进行比较也不能说明方法的优劣。因此,需要进一步研究面雨量计算的检验方法。
5 结论面雨量估算技术研究大概可分为雨量空间分析方法研究和雨量观测技术研究。空间分析模型的基础直接影响流域面雨量估算精度。随着遥感技术发展,地理信息提取技术日趋成熟,借助地理统计方法将影响降水分布的地理因素融入模型,已成为空间插值的主导趋势。而卫星、雷达反演降水技术的不断成熟,非常规降水资料大量用于面雨量计算,则为面雨量的计算研究带来了广阔的发展前景。然而,如何把遥感监测的雨量和地面雨量计观测的降水信息有效地融合在一起,生成有代表性的流域面雨量,仍然是亟待解决的重要问题。
当前,以雷达、卫星估测降水资料为主、结合地面常规降水和自动气象站降水观测资料,快速融合来进行面雨量的估算,已成为流域面雨量估算的发展趋势,在应用非常规观测较早的发达国家中已实现了业务化运行。在我国,由于非常规观测的应用还不够普及,资料积累有限,业务运行中仍以地面常规观测资料为主要估算依据,估算精度和时效性已难以满足水文业务的要求。而以GIS为平台,实现数据管理、分析和显示一体化管理,也代表了面雨量业务系统的发展方向。与世界先进水平相比,我国的面雨量业务系统建设还有不小的差距。
准确的流域面雨量预报是提高洪水预见期的基础。过去,由于对面雨量预报重视不够,定性的降水预报难以满足水文应用的需求。流域面雨量预报是沟通水文预报和气象预报的桥梁。如何提高面雨量预报准确率,是需要我国水文、气象工作者进一步深入研究的重要课题。
| [1] |
徐晶, 林建, 毕宝贵, 等. 七大江河流域面雨量计算方法及应用[J]. 气象, 2001, 27(11): 13-51. |
| [2] |
杨扬, 戚建国. 数字卫星云图估算面雨量的应用试验[J]. 气象, 1995, 21(3): 35-39. |
| [3] |
方慈安, 潘志祥, 叶成志, 等. 几种流域面雨量计算方法的比较[J]. 气象, 2003, 29(7): 23-26. |
| [4] |
王登炎, 李德俊, 金琪. 变分法和卫星云图模式识别在强降水面雨量预报中的应用[J]. 气象, 2003, 29(3): 20-22. |
| [5] |
周筱兰, 张礼平, 王仁乔, 等. 应用最优化订正法制作长江上游面雨量预报[J]. 气象, 2003, 29(3): 31-33. |
| [6] |
毕宝贵, 徐晶, 林建. 面雨量计算方法及其在海河流域的应用[J]. 气象, 2003, 29(8): 39-42. |
| [7] |
潘永地, 姚益平. 地面雨量计结合卫星水汽通道资料估算面降水量[J]. 气象, 2005, 30(9): 28-30. |
| [8] |
徐晶, 毕宝贵. 卫星估计降水量产品的优化处理及分区检验[J]. 气象, 2005, 31(2): 27-31. |
| [9] |
Thiessen A H. Precipitation for Large Areas[J]. Monthly Weather Review, 1911, 39: 1082-1084. |
| [10] |
Bedient P B, Huber W C. Hydrology and Floodplain Analysis[G]. 2nd Ed. Addison-Vesley Reading, MA. 1992.
|
| [11] |
Barnes S L. Mesoscale Objective Analysis Using Weighted Time-series Observations[R]. NOAA Tech. Memo. ERL NSSL-62, National Severe Storms Laboratory, Norman, OK 73069, 1973: 60. https://link.springer.com/article/10.1007%2FBF01025401
|
| [12] |
Cressman G P. An Operational Objective Analysis System[J]. Monthly Weather Review, 1959, 87: 367-374. DOI:10.1175/1520-0493(1959)087<0367:AOOAS>2.0.CO;2 |
| [13] |
Hutchinson M F. Interpolation of Rainfall Data with Thin Pl ate Smoothing Splines-Part Ⅰ: Two Dimensional Smoothing of Data with Short Rang e Correlation[J]. Journal of Geographic Information and Decision Analysis, 1998, 2: 139-151. |
| [14] |
Hutchinson M F. Interpolation of Rainfall Data with Thin Plate Smoothing Splines-Part Ⅱ: Analysis of Topographic Dependence[J]. Journal of Geographic Information and Decision Analysis, 1998, 2: 152-167. |
| [15] |
Daley R. Atmospheric Data Analysis[R]. Cambridge University Press, Cambridge, 1991. https://link.springer.com/article/10.1007%2Fs00190-010-0427-x
|
| [16] |
Cressie N A C. Statistics for Spatial Data[M]. New York: Wiley, 1993: 900.
|
| [17] | |
| [18] |
Goovaerts P. Comparison of Geostatistical Methods for Estimating the Areal Average Climatological Rainfall Mean Using Data on Precipitation and Topography[J]. Int. J. Climate, 2000, 18: 1031-1047. |
| [19] |
Collier C G. Development in Radar and Remote-sensing Methods for Measuring and Forecasting Rainfall[J]. Phil. Trans. R. Soc. Lond. A, 2002, 360: 1345-1361. DOI:10.1098/rsta.2002.1004 |
| [20] |
Joss J,Waldvogel A. Precipitation measurement and hydrology[M]. In: Radar in Meteorology, D. Atlas (Ed.), 1990, AMS,577-606.
|
| [21] |
刘娟, 宋子忠, 刘东风, 等. 分组Z—I关系及其在淮河流域雷达测雨中的应用[J]. 气象科技, 1999, 19(2): 213-220. |
| [22] |
Wyss J, Williams E R. Bras R L. Hydrological Modeling of New England River Basins Using Radar Rainfall Data[J]. J. Geophys. Res, 1990, 95(D3): 2143-2152. DOI:10.1029/JD095iD03p02143 |
| [23] |
Moore R J, Hall M J. HYREX: The Hydrological Radar Experiment[J]. Hydrology and Earth System Sciences, 2000, 4(4). |
| [24] |
COST 717 Final Report. Use of Radar Observations in Hydrological and NWP Models[R]. A. Rossa et al(Eds. ). (http://www.smhi.se/cost717/doc/WDF_MC_200505_1.pdf), 2005.
|
| [25] |
Wood S J, Jones D A, Moore R J. Static and Dynamic Calibration of Radar Data for Hydrological Use[J]. Hydrology and Earth System Sciences, 2000, 4(4): 545-554. DOI:10.5194/hess-4-545-2000 |
| [26] |
Seo D J, Krajewski W T, Bowles D S. Stochastic Interpolation of Rainfall Data from Rain Gages and Radar Using Cokriging.1.Design of Experiments[J]. Water Resources Research, 1990, 26(3): 469-477. |
| [27] |
Patrick E B. Space-time Calibration of Radar Rainfall Data[J]. Appl.Statist, 2001, 50: 221-241. |
| [28] |
Sokol Z. The Use of Radar and Gauge Measurements to Estimate Areal Preci pitation for Several Czech River Basins[J]. Stud.Geophys.Geod, 2003, 47: 587-604. DOI:10.1023/A:1024715702575 |
| [29] |
何健, 王春林, 毛夏, 等. 利用雷达回波与GIS技术反演面雨量研究[J]. 气象科技, 2006, 34(3): 336-339. |
| [30] |
Seo D J. Real-time Estimation of Rainfall Fields Using Radar Rainfall and Rain Gage Data[J]. Journal of Hydrology, 1998, 208: 37-52. DOI:10.1016/S0022-1694(98)00141-3 |
| [31] |
Grimes D I F, Pardo-Igu'zquiza E, Bonifacio R. Optimal Area Rainfall Estimation Using Raingauges and Satellite data[J]. Journal of Hydrology, 1999, 222: 93-108. DOI:10.1016/S0022-1694(99)00092-X |
| [32] |
师春香, 卢乃锰, 张文建. 卫星面降水估计人工神经网络方法[J]. 气候与环境研究, 2001, 6: 467-471. |
| [33] |
刘洪鹏, 刘文. 省域卫星估测降水的资料融合技术及精度分析[J]. 山东气象, 2003, 23(4): 22-24. |
| [34] |
万玉发, 张家国, 杨洪平, 等. 联合雷达网和卫星定量监测与预报长江流域大范围降水[J]. 应用气象学报, 1998, 9(1): 94-103. |
| [35] |
阿迈德·迪狄安·迪阿罗, 刘晓阳, 毛节泰, 等. 卫星雷达联合重构大尺度流域降水场[J]. 高原气象, 2004, 23: 11-17. DOI:10.3321/j.issn:1000-0534.2004.01.002 |
| [36] |
张爱民, 郑媛媛, 郑兰芝, 等. 基于CINRAD和卫星的淮河流域致洪暴雨综合定量估测及预警研究[J]. 热带气象学报, 2006, 22(1): 96-100. |
| [37] |
Goovaerts P. Geostatistical Approaches for Incorporating Elevation Into the Spatial Interpolation of Rainfall[J]. Journal of Hydrology, 1999, 228: 113-129. |
| [38] |
Eulogio Pardo-Iguzqiza. Comparison of Geostatistical Methods for Estimating the Areal Average Climatological Rainfall Mean Using Data on Precipitation and Topography[J]. Journal of Climatology, 1998, 18: 1031-1047. DOI:10.1002/(ISSN)1097-0088 |
| [39] |
刘晓阳, 毛节泰, 李纪人, 等. 雷达估测降水模拟史灌河流域径流[J]. 北京大学学报(自然科学版), 2002, 38: 342-349. DOI:10.3321/j.issn:0479-8023.2002.03.008 |
 2007, Vol. 33
2007, Vol. 33