2. 中国气象局武汉暴雨研究所;
3. 重庆市气象局
2. Wuhan Institute of Heavy Rain, CMA;
3. Chongqing Meteorological Bureau
在分布式模型或统计模型的洪水预报中,流域面雨量都是一个非常关键的因子。降水定量估计和降水定量预报又是流域面雨量计算的重要依据。国内外的气象水文学者从事了大量的雷达定量估测降水研究工作[1-2]。采用适合的Z-I关系进行降水率估计是雷达定量测量降水准确性的一个重要因素。目前,我国新一代天气雷达的降水系列算法中沿用了WSR-88D中设定的由美国夏季深对流云降水统计得到的Z-I关系式,即Z=300I1.4。其中Z为雷达反射率因子,I为降水强度。我国新一代天气雷达的所有降水估算产品也是基于该Z-I关系得到的。由于Z-I关系随季节和地区变化较大[3],WSR-88D中的Z-I关系式在淮河流域是否适用还需深入分析。如何统计得到适合于淮河流域梅雨期积层混合云降水的Z-I关系,应用于新一代天气雷达定量估测降水业务,是当前急待解决的问题。
利用2003年汛期合肥CINRAD/SA雷达资料和地面1小时雨量观测数据,分别采用整体优化和分段优化两种方案得到Z-I关系,对淮河支流淠河灌区的水源地佛子岭流域和响洪甸流域进行降水定量测量。结合地面雨量资料,对比分析了这两种方案对雷达定量测量降水及其流域面雨量计算结果的影响。
1 观测资料和试验区域 1.1 观测资料研究资料的时段为2003年6月20日00时—7月12日00时(世界时,下同)。雷达数据来源于“淮河黄河流域暴雨洪水监测预报系统试验”项目和“973中国·暴雨”外场试验采集的合肥新一代天气雷达体扫资料,间隔约6分钟。雨量数据来自“淮河黄河流域暴雨洪水监测预报系统试验”项目中由气象部门和淮河水利委员会提供的地面逐小时雨量资料。
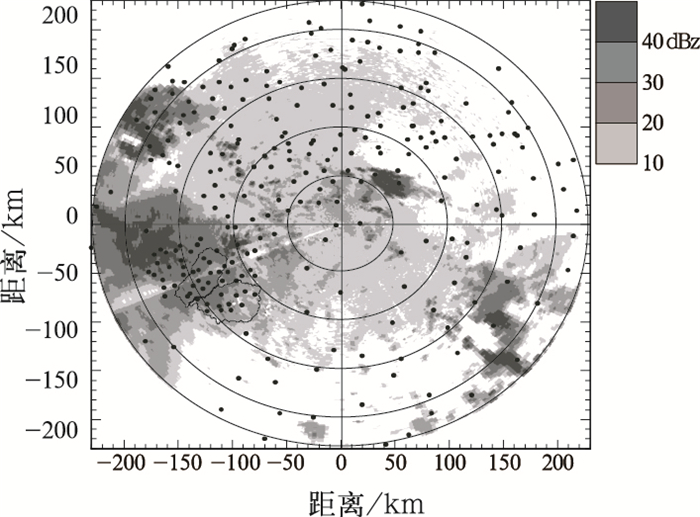
1.2 试验区域统计Z-I关系的区域为以合肥雷达为中心,距离在50~120km的环形区域(见图 1)。图 1为2000年6月1日21:33合肥CINRAD/SA雷达最低仰角观测的基本反射率图像,图中距离圈间隔50km,最外圈距离为230km。
|
图 1 2000年6月1日21:33 GMT合肥CINRAD/SA雷达最低仰角观测的基本反射率分布图 图中黑色圆点表示气象部门和淮河水利委员会的雨量计位置。淠河流域(合肥西南)中的两个子闭合流域,偏北为响洪甸流域,偏南为佛子岭流域 |
面雨量测量区域为淠河灌区的水源地,即响洪甸水库控制和佛子岭水库的控制流域。两个流域均位于合肥雷达的探测距离110~140km之间(见图 1中雷达西南的两个闭合实线区),面积分别为1410km2和1813km2。受西南方向地形影响,在合肥雷达低仰角观测中,响洪甸流域的波束阻挡比佛子岭流域的波束阻挡要严重得多。这是造成图 1中响洪甸流域反射率图像不连续的主要原因。
2 波束阻挡订正雷达资料预处理,主要包括孤立点剔除、畸异回波检测、阻挡订正、构成复合平面。由于雷达周围高大山脉或者建筑物会部分阻塞或者完全遮挡住雷达的电磁波能量,在利用低仰角的雷达观测数据进行降水定量测量时,必须考虑雷达波束的阻挡订正。在国内外的诸多文献中都研究过阻挡订正方法[4]。在新一代天气雷达的降水观测模式中,雷达最低仰角的电磁波发射和接收都稳定在0.5°附近。而在实际探测中,合肥雷达天线存在低垂现象,最低仰角在0.22°到0.26°之间变化。显然不能根据0.5°仰角的遮挡情况进行阻挡订正。先根据由实际观测的仰角值和方位值计算的各个距离库的波束阻挡系数,再采用Fulton波束阻挡订正方案对雷达最低仰角的回波强度观测数据进行补偿。
3 最优化Z-I关系的建立 3.1 Z-I关系最优化方法设所有雨量计观测的1小时降水记录总数为N,观测值用Gn表示,n=1, 2, …N。对第n个雨量值Gn来说,有M个与之时空相对应的雷达回波强度ZdBnm, m=1, 2, …M。根据雷达反射率因子和降水强度之间的关系式Z=AIb,可将ZdBnm转化为降水强度Inm,即
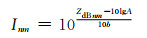
|
(1) |
对降水强度进行时间积分就可以得到雷达测量的1小时降水。记为Rn,n=1, 2, …N。根据文献[5]计算公式如下:
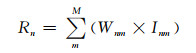
|
(2) |
其中,Wnm是资料所代表的时间权重系数,根据雷达观测时间确定。
选取判别函数
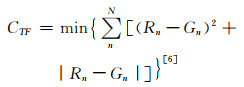
|
(3) |
参数A从10到1000,步长为1;参数b从0.5到5,步长为0.1;对应于每一个A和b值,就得到一个CTF值;对式(1)中A和b作循环,CTF最小时对应的参数A和b值所决定的Z-I关系就是最优的。
3.2 Z-I关系最优化的两种方案利用上述方法,采用两种方案建立最优化的Z-I关系。
第一种方案只采用一组Z-I关系,先循环调整式(1)中A和b的值,再利用式(2)计算出雷达测量降水值;最后根据式(3)确定出最优化的Z-I关系。
第二种方案则通过一个事先给定的回波强度阈值,分别在低值区(回波强度小于该阈值)和高值区(回波强度大于该阈值)采用两组不同的Z-I关系,先比较实际回波强度与该阈值的大小确定采用哪组Z-I关系代入式(1)中计算降水强度后,再利用式(2)计算出雷达测量降水值。通过两组Z-I关系中A和b值的循环,最后根据式(3)确定出低值区和高值区的两组最优化Z-I关系。
与第一种方案相比,第二种方案在利用回波强度估计降水强度时,设定了一个回波强度阈值,将回波强度值区间分为两段进行Z-I关系优化,称为“分段最优方法”。而第一种方案在整个回波强度值区间上进行优化,故称为“整体最优方法”。
3.3 最优化Z-I关系的确定利用2003年7月8日00时至2003年7月11日13时的观测资料建立合肥雷达测量降水的最优化Z-I关系。
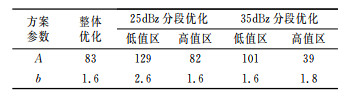
首先,在以合肥雷达为中心,距离雷达站50~120km的环形区域内选择33个观测站的1小时雨量数据作为G值。剔出低于1mm·h-1的数据后,得到的1小时降水观测记录总数为932,即N=932,其中在1~2mm·h-1时记录数为232,2~5,5~10,10~15,15~20mm·h-1的记录数分别为318、249、90、29。然后采用整体最优方法和分段最优方法两种方案建立计算最优化的Z-I关系。为了检验分段最优方法的效果,分别将回波强度阈值设定为25dBz和35dBz进行优化。两种方案得到的最优Z-I关系式系数见表 1。
|
|
表 1 整体最优方法和分段最优方法确定的最优Z-I关系式系数 |
采用与建立最优化Z-I关系中所用观测资料的相同时段和相同区域内的另外15个雨量站资料进行检验。
检验方法一:雷达定量降水估算得到的雨量值跟雨量计值作散点图,比较它们的相关系数及其斜率。
检验方法二:雨量按大小分成若干段,在任一段上,对雨量计值求平均,同时把相对应的雷达估算值求平均,再求雷达估算平均值与雨量计平均值的比值(ri)。若比值接近于1,说明雷达估算值接近于雨量计值,若大于1,说明雷达估算值高估,反之,就是低估。
检验方法三:检验分段优化时,由检验方法二分别得到分段优化和整体优化与雨量计的比值,再对分段优化比值与整体优化比值作差值比较(Δri)。
4.1.1 整体最优法与Z=300I1.4的比较对15个雨量站2003年7月8日00时至7月11日00时分析:
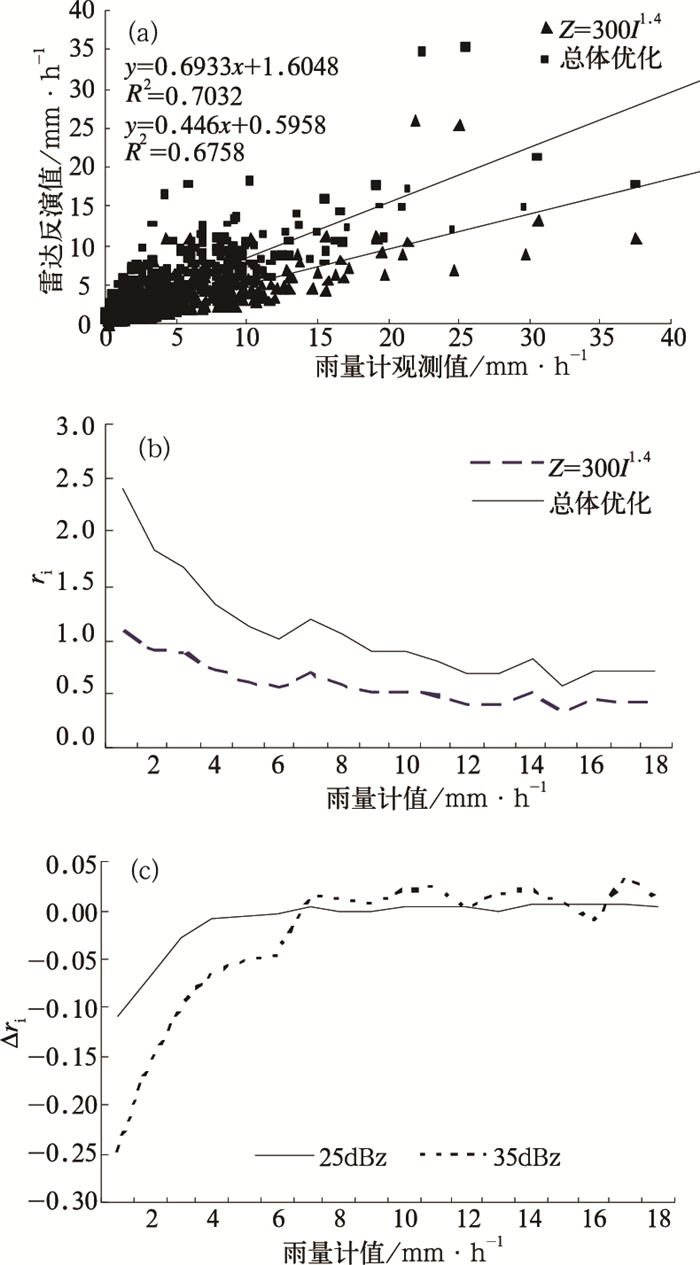
(1) 由图 2a散点图得到Z=300I1.4与雨量计的相关系数和斜率分别为0.82、0.45;整体优化后相关系数和斜率分别为0.83、0.69。相关系数仅提高了0.1,但是斜率却从0.45提高到0.69。
|
图 2 2003年7月8日00时至7月11日00时雷达反演与50~120km内15个雨量站资料比较 (a)整体优化Z-I和Z=300I1.4关系与雨量计的散点图比较,(b)整体优化Z-I关系和Z=300I1.4关系分别与雨量计比值的分段比较,(c) 2种不同分段最优方法与雨量计的比值跟整体优化与雨量计比值的差值比较 |
(2) 由图 2b可知,整体优化Z-I关系得到的雷达观测值与雨量计的比值都比Z=300I1.4的高,比值在1附近;而Z=300I1.4比值曲线在0.5左右,雷达观测值低估严重。
在0~2mm·h-1内,整体优化后的雷达观测值和雨量计的比值大于1,;在2~13mm·h-1时,雷达反演值较好,比值接近1;在13mm·h-1以上雷达反演值低估严重,比值达到了0.6。用Z=300I1.4关系式时在0~2mm·h-1时,比值在0.9~1.1之间;在4mm·h-1以上时雷达反演值低估严重,比值都在0.5附近。
4.1.2 分段最优法与整体最优法的比较从图 2b中可以看出,整体最优法在2mm·h-1以下时造成一定程度的高估,在2~6mm·h-1比值大于1,7mm·h-1以上比值小于1。因此,采用了分段优化,分别以25dBz和35dBz为阈值进行分段优化,并对2种不同的分段优化法进行比较。由图 2c中得出:在整体优化0~6mm·h-1之间比值大于1时,35dBz分段优化得到的比值比25dBz分段优化得到的比值降低明显,尤其在2mm·h-1附近时达到-0.25;在整体优化8mm·h-1以上比值小于1时,35dBz分段优化得到的比值增幅更为明显,在0~0.04之间。
另外,整体优化、25dBz分段优化、35dBz分段优化与雨量计的相关系数分别为0.83、0.839、0.846,均高于Z=300I1.4的相关系数0.82。可见,35dBz分段优化比其他两者的优越。因此,在以后用到的优化Z-I关系都是指35dBz分段优化得到的。
4.2 不同时段不同雨量站检验检验资料由气象部门提供的合肥新一代天气雷达体扫资料,间隔约6分钟,及对应时段上地面逐小时雨量资料。选取了2组检验数据,检验一时段为2006年6月21日00时至6月25日00时14个雨量站,检验二时段为2006年7月3日00时至7月6日00时18个雨量站。雨量站位置是在以合肥雷达为中心、距离雷达站50~120km的环形区域内选取。
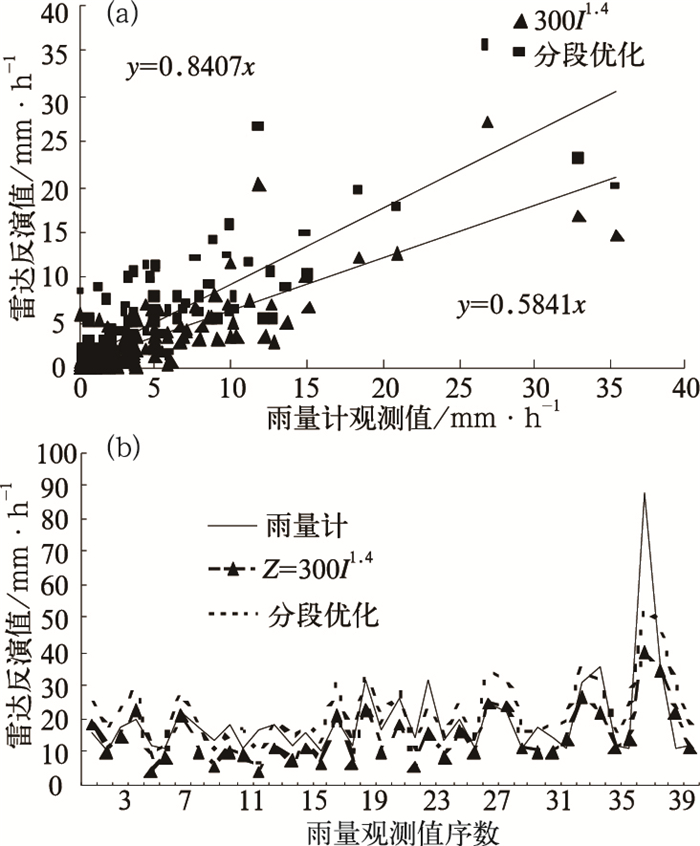
(1) 由检验一图 3a散点图得到Z=300I1.4与雨量计的回归线斜率分别0.58;分段优化后斜率为0.84。检验二分段优化后的斜率从0.56提高到了0.81。
|
图 3 (a) 检验一:2006年6月21日00时至6月25日00时,分段优化Z-I关系和Z=300I1.4关系与雨量计的散点图比较(b)检验二:2006年7月3日00时至7月6日00时,小时雨量大于10mm·h-1的雨量图比较 |
(2) 检验一小时雨量大于5mm·h-1雨量计、Z=300I1.4、分段优化后三者的累积值分别为437mm、262mm、405mm。Z=300I1.4低估了40%,而分段优化后只低估了7%。检验二小时雨量大于10mm/h雨量计、Z=300I1.4、分段优化后三者的累积值分别为818mm、580mm、860mm。Z=300I1.4低估了39%,而分段优化后高估5%。
(3) ERMS(Root Mean Squared Error)为均方根误差,用于了解雷达估测值与实际值的离散程度,其值越小离散程度越小。
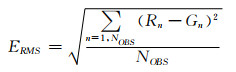
|
式中NOBS为观测值达到给定阈值的总数目,Rn是对应的雷达反演的降水量,Gn是某点雨量计观测的降水量。检验一阈值为5mm·h-1时,分段优化后ERMS从6.5mm·h-1降低到了5.2mm·h-1;检验时段二阈值为10mm·h-1时,分段优化后ERMS从9.8mm·h-1降低到了8.3mm·h-1。
(4) 比较小时雨量图(检验一图略)。从图 3b小时雨量大于10mm·h-1的雨量图可以看出,大部分优化后得到的小时雨量更接近于雨量计值,尤其在峰值区,分段优化后得到的雨量值明显高于Z=300I1.4。例如,雨量计观测值为25.7mm·h-1时,Z=300I1.4和分段优化后的雨量值分别为18和27mm·h-1。
从以上检验总的来看,用整体Z-I关系尤其是35dBz分段优化比Z=300I1.4的要优越得多,且比较稳定。
5 分段优化法在面雨量测量中的应用选取2003年6月20日00时至7月12日00时响洪甸流域其中的72小时面雨量系列和佛子岭流域528小时的面雨量系列进行比较。
5.1 响洪甸面雨量比较在2003年6月20日00时至7月12日时时段上共528小时的时间序列上选取第433~504期间72个小时的响洪甸小时面雨量情况分析,如图 4。其中雨量计得到的流域面雨量是采用距离平方反比法得到(下同)。
|
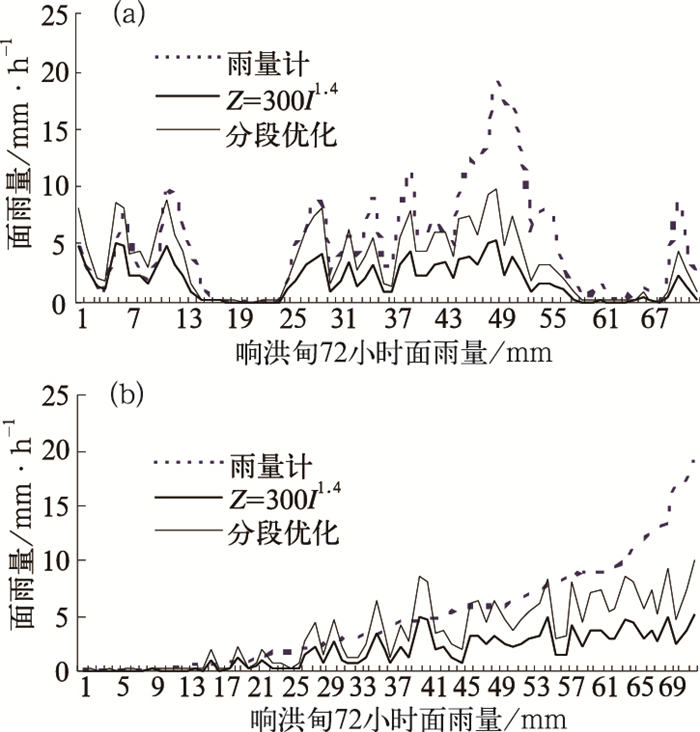
图 4 (a) 响洪甸流域72小时面雨量分布;(b)分段优化和Z=300I1.4关系得到的流域面雨雨量与雨量计得到的流域面雨量曲线图比较 按照雨量计面雨量从小到大的顺序排列 |
(1) 从图 4a中可以看出,用分段优化法和Z=300I1.4反演的面雨量和雨量计反演的面雨量值趋势非常接近。在雨量计小时面雨量在10mm·h-1附近时,分段优化法得到值普遍比Z=300I1.4的高3~5mm·h-1;最高雨量计峰值为19.7mm·h-1,Z=300I1.4反演的值为5.3mm·h-1,分段优化法反演的值为10mm·h-1。分段优化法在峰值区更接近于雨量计的值,但是低于雨量计的值。
(2) 由图 4b可看出,面雨量在8mm·h-1以下时,分段优化法的雷达观测值与雨量计的值接近,但是面雨量在8mm·h-1以上时,雷达观测值低估严重。分段优化法与雨量计的相关系数0.81比Z=300I1.4的0.78提高了3%;与雨量计的回归线斜率0.52比Z=300I1.4的0.28提高了0.24。
(3) 雨量计累积值为343mm,分段优化法和Z=300I1.4的累积值分别为250、135mm,它们的累积面雨量低估值分别为27%和61%。
5.2 528小时流域面雨量比较在2003年6月20日00时至7月12日00时时段上共528小时时间序列上流域小时面雨量情况分析(这里以佛子岭为例),如图 5所示。
|
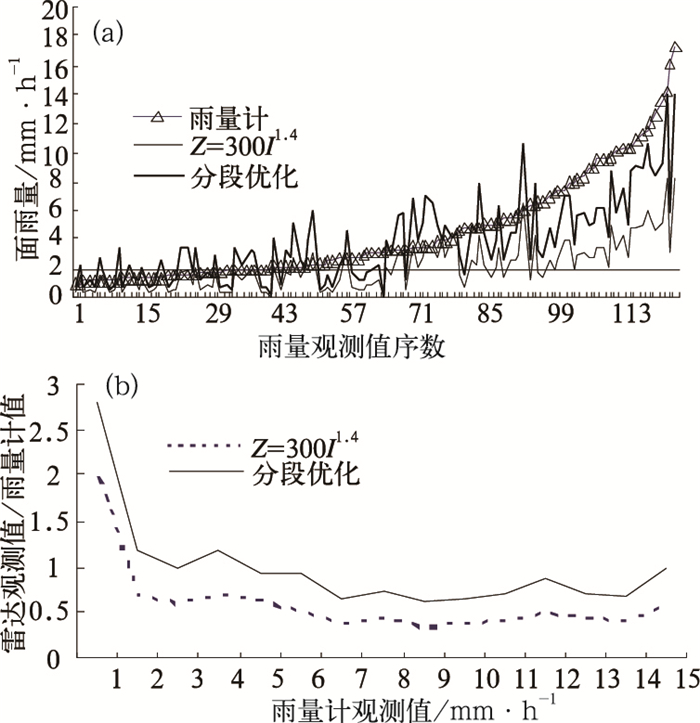
图 5 2003年6月20日00时至7月12日00时佛子岭流域的面雨量分布 (a)雨量计面雨量大于1mm·h-1时分段优化法和Z=300I1.4得到的佛子岭流域面雨量分布,按照雨量计面雨量从小到大的顺序排列(b)分段优化法和Z=300I1.4得到的面雨量系列与雨量计得到的面雨量比值分段比较 |
(1) 从图 5a中可以看出,分段优化法得到的小时面雨量比用Z=300I1.4得到的要高,在雨量计小时面雨量达到10mm·h-1附近时,分段优化法得到的值普遍比Z=300I1.4的高2~5mm·h-1左右。
(2) 从分段优化法和Z=300I1.4与雨量计相关系数分别为0.86、0.89,相关系数提高了3%;同时与雨量计的回归线斜率从0.4提高到0.72。
(3) 从图 5b得出分段优化法与雨量计的比值曲线都比Z=300I1.4的高,在1mm·h-1以上时比值更接近于1;而Z=300I1.4的比值都在1以下,在0.5附近,其低估程度很严重。但是在0~1mm·h-1小雨时雷达反演值高估,分段优化法高估更严重。
(4) 对雨量计小时面雨量大于1mm·h-1相应的雷达反演值累积比较。雨量计累积值为553mm,分段优化法和Z=300I1.4的累积值分别为474、267mm。可见,优化Z-I关系之后,对于面雨量大于1mm·h-1的累积面雨量相对于雨量计的值从48.4%提高到了85.9%。
6 结论通过整体最优Z-I关系和分段最优Z-I关系得到淮河流域梅雨期积层混合云降水的Z-I关系,并对佛子岭和响洪甸流域进行面雨量的应用,通过检验以及进行不同的试验分析得到以下几点结论:
(1) 整体最优法尤其是分段最优法比Z=300I1.4要优越,从样本总雨量检验、雨量站过程雨量、流域平均小时雨量和雨量计的相关系数和回归线斜率都说明了这一点。
(2) 强降水阶段流域面雨量比较。分段最优法得到的流域累积面雨量与雨量计的比值从39%提高到73%;其小时面雨量的峰值也更接近于雨量计的值;分段最优法的相关系数从0.78提高到0.81;同时,与雨量计的回归线斜率从0.28提高到了0.52。
(3) 在强降水时刻,流域平均面雨量达到10mm·h-1附近时,分段最优法反演的值能从3~6mm·h-1提高到6~10mm·h-1。
(4) 528小时时间序列上佛子岭流域面雨量比较。分段最优法得到的流域平均面雨量与雨量计的相关系数从0.86提高到0.89,回归线斜率从0.4提高到0.72。面雨量10mm·h-1以上时,分段最优法得到的面雨量仍然低估比较严重。1mm·h-1以上流域平均面雨量累积值与雨量计累积值的比值从48.4%提高到了85.9%。
总之,在淠河灌区的水源地,响洪甸流域和佛子岭流域内,在梅雨期采用分段最优法时雷达测量降雨精度提高很大。
| [1] |
伍志方, 戴铁丕, 张培昌. 天气雷达定量测量区域降水量的校准技术及误差分析[J]. 气象, 1991, 17(10): 9-14. DOI:10.7519/j.issn.1000-0526.1991.10.002 |
| [2] |
陈秋萍, 余建华, 杨林增, 等. 闽中北前期多普勒雷达定量故测降水分析[J]. 气象, 2006, 32(4): 56-61. DOI:10.7519/j.issn.1000-0526.2006.04.010 |
| [3] |
张培昌, 杜秉玉, 戴铁丕. 雷达气象学[M]. 北京: 气象出版社, 2001: 181-184.
|
| [4] |
Fulton R.A., Breidenbach J.P., Seo D., et al. The WSR-88D Rainfall Algorithm[J]. Weather and Forecasting, 1998, 13: 377-395. DOI:10.1175/1520-0434(1998)013<0377:TWRA>2.0.CO;2 |
| [5] |
李建通, 郭林, 杨洪平. 雷达-雨量计联合估测降水初值场形成方法探讨[J]. 大气科学, 2005, 29(6): 1010-1020. |
| [6] |
Simth, P. Letal. Derivation of an R-Z relationship by compwter optimization and its use in measuring daily areal rainfall[C]. 16th radar Mete conf, 1975, 461-466.
|
 2007, Vol. 33
2007, Vol. 33