2. 国家气象中心;
3. 北京大学大气科学系
2. National Meteorological Center;
3. Department of Atmospheric Sciences, Peking University
云通过影响太阳和地球辐射,对整个地气系统的能量平衡具有强烈的调节作用。然而,云的宏微观物理特性在空间和时间上差异很大,若能细致了解云的微物理特征参量不仅有助于对全球气候变化的研究,有助于对天气系统的监测预报,有助于对人工影响天气作业条件和效果检验的判定,同时对认识人类活动对环境造成的影响也十分重要。
云粒子有效半径是重要的云物理特征参量。近几年来,国内外许多学者在利用极轨卫星反演云粒子有效半径方面做了大量工作。Nakajima[1]提出了一种利用双通道的反射信息反演层云光学厚度和云粒子有效半径的方法。Rosenfeld等[2]利用NOAA上的AVHRR数据反演云顶附近的云粒子有效半径,通过与雷达回波的对比发现,3.7μm的辐射中确实包含降水云云顶粒子物理状态的信息。他利用这一反演方法分析了城市和工业污染对降水的影响[3],分析了播撒作业之后,云微物理特性的变化[4]。赵凤生等[5]开发出利用NOAA -AVHRR资料同时反演云的光学厚度和云滴有效半径的迭代方案。刘健等[6]利用FY-1C资料反演了水云的粒子有效半径。但极轨卫星一天只有两个时次的过顶观测资料,这对于追踪某一特定云系,或着眼于某一感兴趣的区域来说,是远远不能满足要求的。MODIS也有云的微物理特征产品(光学厚度、粒子尺度、液水路径等),并且应用较为广泛,但MODIS每两天才提供一次全球范围的数据,时间频次低。因此还应开发高时间分辨率基于静止卫星的相应产品。
李娟、毛节泰等曾利用GMS-5静止卫星资料反演云的微物理特性,但限于此类静止卫星缺乏对有效粒子半径敏感的中红外(3.7μm)波段,对云粒子有效半径的反演存在着一定的困难。
我国自行研发的FY-2C静止卫星2005年6月1日正式投入业务运行。它拥有较高的时间频次(通常为1小时1次,汛期加密为半小时1次),较丰富的观测通道(包括:0.3~11.3μm,11.5~12.5μm,6.3~7.6μm,3.5~4.0μm,0.55~0.90μm等5个通道观测资料),为研究云参数提供了较丰富的信息。其中,中红外4通道对云滴大小分布非常敏感,为此,本文主要利用FY-2C静止卫星中红外通道(3.5~4.0μm)的观测数据结合其它通道的观测,进行水云粒子有效半径的反演计算和实验。
1 计算原理对于水汽吸收波段, Lambertain面上很厚的光学云层的大气反射函数可表达为
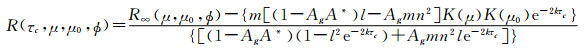
|
(1) |
式中,k是散射指数(特征向量),用于描述由于散射而导致辐射衰减的程度,A*是半无限大气的球面反照率,m,n,l为常数。上述5个参数都与单次散射反照率ω0紧密相关,而与g的关系比较小。k、A*、m、n和l 5个参数可综合用相似参数s表示
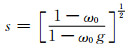
|
(2) |
从式(1)可以看出,在水汽吸收波段,具有厚光学厚度云层的反射特性可主要由光学厚度τc和相似性参数s两个参数确定,其中s主要与有效粒子半径有关,粒子有效半径可定义为
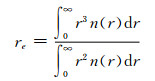
|
(3) |
它在描述云滴尺度方面很有物理意义。研究发现,对于明显的降水来说,云滴的有效半径至少要达到12μm[6]。
式(3)中n(r)是粒子大小分布,r是粒子半径。
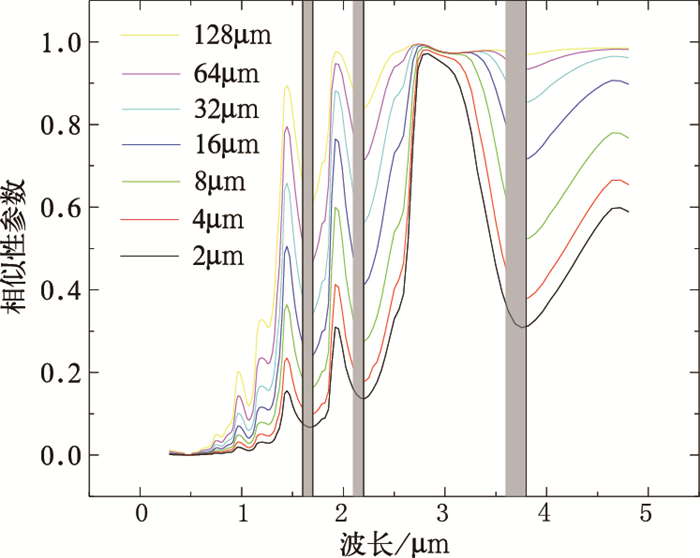
图 1显示了利用Mie理论及液水折射指数计算得到的含有不同有效半径尺度的水云的相似性参数随波长的变化关系,因相似性参数与水汽吸收波段的反射函数密切相关,因此反射函数本身必定对粒子尺度有类似的敏感性。可以看出,相似性参数,或者说是反射函数,在1.64、2.13和3.75μm波段,对粒子大小比较敏感,可以利用这些波段来反演云粒子有效半径。这与上面公式分析中得到的结论一致。
|
图 1 各种尺度云粒子(2、4、8、16、32、64、128μm)相似性参数随波长的变化 |
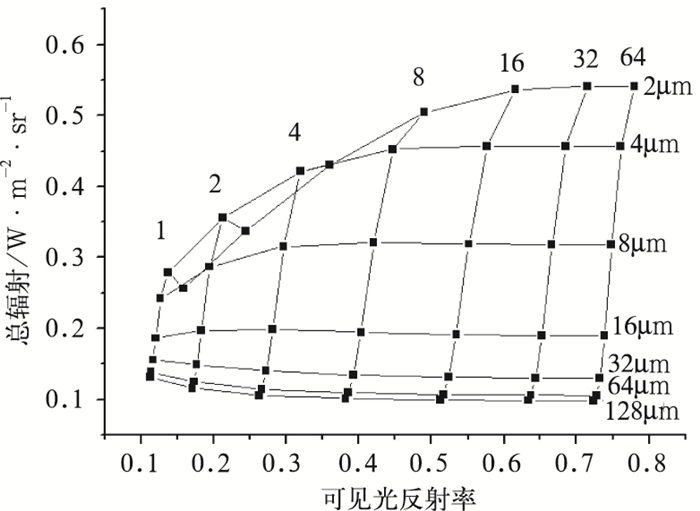
如图 2,通过SBDART[7]云模式计算不同光学厚度τ和粒子有效半径re条件下,0.65μm通道反射率和3.75μm通道的全辐射值发现,3.75μm通道全辐射值随re的变化十分显著,粒子越大,全辐射值越小,而与τ的变化关系很小,说明3.75μm通道全辐射值同样可以反映云粒子的尺度变化。刘健[8]等曾指出,采用0.65μm通道反射率和1.6μm通道反射率,0.65μm通道反射率和3.75μm通道全辐射值两种不同的通道组合,粒子有效半径反演间的差异不是很大(小于6%),可以利用后者进行云粒子有效半径的反演。对于不同的太阳天顶角、太阳方位角和卫星观测天顶角、卫星观测方位角,都有同样的规律,因此这种方法适用于FY-2C覆盖范围内的任何地区、任何日间时次(除去太阳天顶角或卫星观测天顶角过大的情况),选取其中的一组进行作图。
|
图 2 可见光通道反射率和红外4通道的总辐射值随云光学厚度和云滴有效半径变化关系 (参数设置:地表为洋面,云顶高度5km,大气模式为中纬度夏季,中心位置观测天顶角61.992°,太阳天顶角28.661°,相对方位角68.679°) |
利用SBDART来计算发射和反射的辐射,输入波长为0.65μm和3.7μm,同时选取FY-2C光谱响应函数作为模式的输入参数。假定:(1)云滴尺度分布为对数正态型。(2)云顶为水平均一,而且充满整个视野。(3) 3.7μm的光学厚度为无穷。(4)忽略云顶以上的大气。
由于3.7μm的辐射既依赖于半径又依赖于相态,因此不可能从卫星观测中同时反演出相态和半径,为了反演半径,必须先假定相态(水云)。可见光通道数据用来挑选适合于利用3.7μm通道数据进行反演的像元,即反射率>40%。根据模式计算的结果,这样的像元在可见光通道的光学厚度至少为5,这就保证了它3.7μm通道具有更大的光学厚度。Arking and Childs[9]已经证明,在3.7μm通道,光学厚度如果>5,则反演的过程中可看作无穷厚。然而, 为了让反演方法具有业务上的应用价值, 我们将条件适当放宽, 对反射率大于25%的像元都进行了反演。
反演云滴有效半径的步骤:
(1) 选择卫星图像上光学厚度大的像元:即可见光通道的反射率>25%,红外1通道的温度低于7℃。
(2) 去除云顶温度过低的像元:过低的云顶温度通常反映云顶全由冰晶组成,因此我们选取红外1通道的温度高于-40℃的像元。
(3) 利用模式计算指定太阳天顶角θ0、相对方位角Φ、卫星天顶角θ以及地表反射率和大气模式条件下的查算表。
(4) 将FY-2C两通道的值内插至查算表中,反演云粒子有效半径。
3 影响因子(误差来源)(1) 光学厚度和观测角度
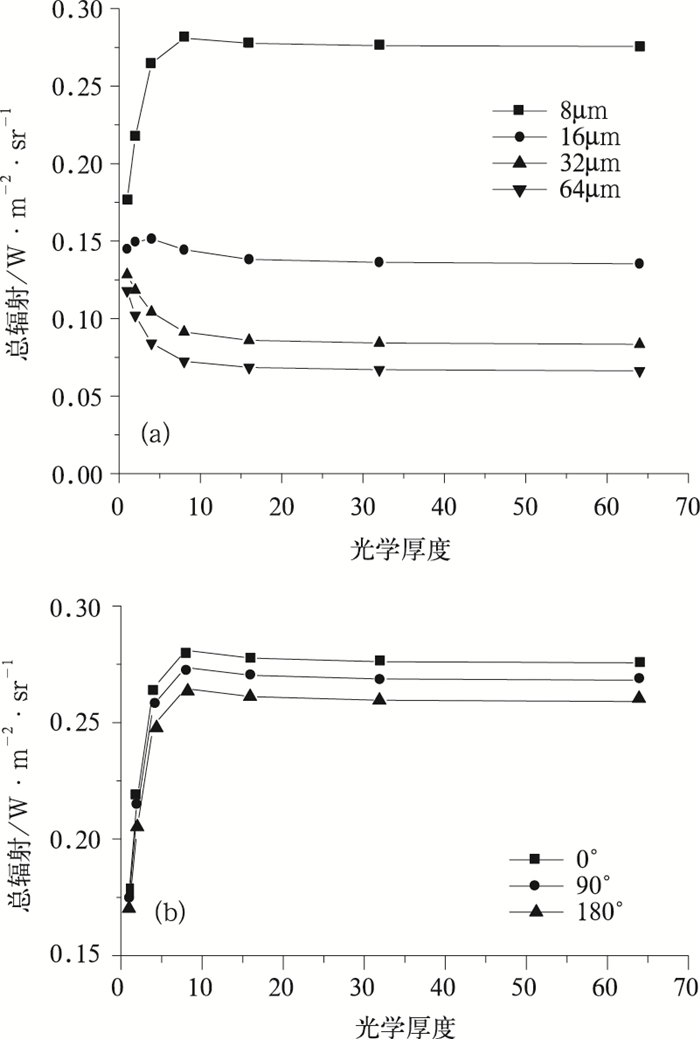
图 3中给出了3.75μm通道总辐射量分别随τ和re的变化曲线。从结果中可以看出,主要依赖于3.75μm通道总辐射量的有效半径,反演结果与光学厚度关系不大,除非光学厚度很小(τ≤4)。并且,从图 3中我们看到,总辐射量随相对方位角的增加而略有减少。
|
图 3 (a) re分别为8、16、32、64μm时, 总辐射量随τ的变化(θ0=10°,Φ=0°,θ=30°)(b)观测的相对方位角分别为0°、90°、180°时, 总辐射量随τ的变化(re=8μm、θ0=10°、θ=30°) |
也就是说,在光学厚度不是很小的情况下,可以独立地反演云粒子有效半径。
(2) 地表反照率误差
经研究发现,地表反照率的误差对3.75μm通道总辐射量没有影响。
(3)辐射测量误差
Nakajima[10]曾指出,在反演有效半径时,较小的太阳天顶角和前向散射时误差较小,而较大的太阳天顶角和后向散射时误差较大。有效半径的反演误差与粒子半径密切相关,当1≤re≤4μm时,若3.75μm通道总辐射量测量误差为5%,无论光学厚度为多少,反演的有效半径误差都会存在一个高值区,超过100%。而在这个有效半径区域两侧,反演误差会迅速减少。
(4)垂直层结非均一性的影响
在前面的反演过程中,假定云层是平面平行、垂直均一的。因地球水云有明显的垂直向非均一性,研究垂直层结对太阳辐射的影响至关重要。许多研究发现,除光学厚度很薄的夹卷区外,云中的液水含量和有效半径都随高度线性增加。可以推断,我们反演的有效半径rremote要小于云顶的有效半径rt而大于云底的有效半径rb。结果显示,在垂直向均一的模式中,rremote一般为rt的85%~95%,而在垂直向非均一的模式中,这个比值为72%~90%。而且,随着τ的增加,rt的减小,rremote越来越接近rt。
综合来说,在τ≥4和re≥8μm的情况下,各方面的误差对反演结果的影响都不是很大, 反演结果会比较可信。
4 与MODIS反演结果的比较为了考察上述反演方法的可行性,将该方法的反演结果与MODIS的产品进行了比较。MODIS包含云粒子有效半径的产品编号为MOD06,在反演之前已经通过其它通道获取了云量和云相态方面的信息。反演基础是云在水汽吸收的近红外波段,反射函数主要是云粒子大小的函数。
选取2006年8月1日10:00时(北京时)的FY-2C数据作为个例,计算云粒子有效半径。区域为32~37°N、138~143°E。FY-2C的数据为0.05°×0.05°的资料,由于MODIS资料较为细致,为了与FY-2C的数据在空间分辨率上保持一致,将MODIS资料插值为0.05°×0.05°的分辨率。
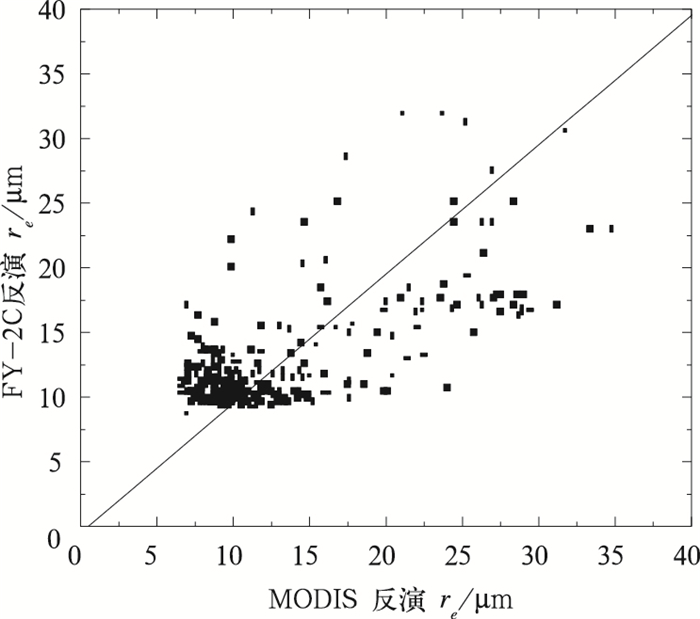
由于该方法主要适用于水云的反演,而FY-2C本身缺乏能有效判定相态的通道1.64μm或2.13μm,因此我们与MODIS产品MOD06_L2.A2006213.0155.004.2006215211214中已判定为水云的像元进行了比较。图 4为FY-2C反演得到的云粒子有效半径与MODIS产品相应结果的对比。相关系数R=0.65607,SD=4.92857, N=295, P<0.0001Y=X-0.49763并对相关系数进行了统计检验,发现通过了显著性水平0.05的检验,说明两种资料所反映的云粒子有效半径的分布具有较好的时空一致性。
|
图 4 FY-2C与MODIS反演的有效半径的比较 |
有效粒子半径的差异原因在于:
(1) 反演选取的通道不同:MODIS利用0.645,2.13和3.75μm通道反射率的组合来反演陆面上空云的微物理特性(海面上空用0.858μm代替0.645μm,雪面和海冰面上空用1.24μm代替0.645μm);而FY-2C是利用3.7μm通道的总辐射值来反演云粒子有效半径。
(2) 不同的仪器具有不同的定标参数。
(3) 不同通道的权重函数不同,反演时会具有一定的差别,理论上严格解释这种差别是比较困难的。
(4) 极轨卫星与静止卫星的空间分辨率不同,MODIS更易看到云的细微结构。
(5) 时间上略有偏差。
5 结论与讨论利用FY-2C资料,结合辐射传输模式,定量地反演了云粒子的有效半径。介绍了具体的原理方法, 分析了误差的可能来源, 并与MODIS的反演结果进行了比较。由于模式中采用的云粒子的正态对数分布, 云粒子为球形水滴, 云覆盖面积广阔及垂直层结均一等假设条件都会对计算结果产生影响。而其它输入数据如地面反射率、像元地理位置、大气廓线等的不确定性也是产生误差的一个原因。另外, 由于辐射传输方程的非线性,没有唯一解存在,实际观测值与理论值间进行拟合插值时,同样会有误差产生。而实际的卫星观测值本身由于观测仪器及数据预处理阶段的问题,会使数据带有一定的误差。
但是可以看到,尽管有这些目前无法避免的误差来源,FY-2C与MODIS的反演结果仍然具有一定的一致性。随着其它物理参数精度的提高及辐射传输模式的改进,将更准确地反演云的微物理特性。再凭借着FY-2C时间频次高的优势,会对人影作业及环境污染方面提供有效的指导和监测。
| [1] |
Nakajima T., King M.D.. Determination of the Optical Thickness an d Effective Particle Radius of Clouds from Reflected Solar Radiation Measurements.PartⅠ:Theory[J]. Journal of the Atmospheric Sciences, 1990, 47: 1878-1893. DOI:10.1175/1520-0469(1990)047<1878:DOTOTA>2.0.CO;2 |
| [2] |
Rosenfeld D., Gutman G.. Retrieving microphysical properties near the tops of potential rain clouds by multispectral analysis of AVHRR data[J]. Atmospheric Research, 1994, 34: 259-283. DOI:10.1016/0169-8095(94)90096-5 |
| [3] |
Rosenfeld D.. Suppression of Rain and Snow by Urban and Industrial Air Pollution[J]. Science, 2000, 287(5459): 1793-1796. DOI:10.1126/science.287.5459.1793 |
| [4] |
Rosenfeld, D., Woodley, W. L. and Krauss, T., Satellite Observations of the Mi crostructure of Natural and Seeded Severe Hailstorms in Argentina and Alberta[M]. 15th Conference on Planned and Inadvertent Weather Modification. AMS, Albuquerque, New Mexico, 2001, p. 68-74.
|
| [5] |
赵凤生, 丁强, 孙同明, 等. 利用NOAA-AVHRR观测数据反演云辐射特性的一种迭代方法[J]. 气象学报, 2002, 60: 594-601. |
| [6] |
Hallett J., Mossop S.C.. Production of secondary ice particles during the riming process[J]. Nature, 1974, 249: 26-28. DOI:10.1038/249026a0 |
| [7] |
Ricchiazzi P., Shiren Yang, Cautier C.. SBDART: A Research and Teaching Software Tool for Plane-Parallel Radiative Transfer in the Earth's Atmosphere[J]. Bulletin of the American Meteorological Society, 1998, 79: 2010-2144. |
| [8] |
刘健, 董超华, 张文建. 利用FY-1C资料反演水云的光学厚度和粒子有效半径[J]. 红外与毫米波学报, 2003, 22: 436-440. DOI:10.3321/j.issn:1001-9014.2003.06.009 |
| [9] |
Arking A., Child J.D.. Retrieval of cloud cover parameters from multispectral satellite images[J]. J. Clim. Appl. Meteorol., 1985, 24: 322-333. DOI:10.1175/1520-0450(1985)024<0322:ROCCPF>2.0.CO;2 |
| [10] |
Nakajima T., Spinhime J. D., Radke L. F.. Determination of the optical thickness and effective particle radius of clouds from reflected solar radiation measurements. Part Ⅱ: Marine stratocumulus observations[J]. J. Atmos. Sci, 1991, 48: 728-750. DOI:10.1175/1520-0469(1991)048<0728:DOTOTA>2.0.CO;2 |
 2007, Vol. 33
2007, Vol. 33