随着国民经济的高速发展,很多大型基建项目需要进行抗风设计,如大型桥梁、高耸建筑物、港口、码头、仓储等。在抗风设计过程中,目前国内外普遍应用极值Ⅰ型分布函数进行极值风速的概率计算。本文主要讨论极值Ⅰ型分布的3种常用参数估计方法:矩法、耿贝尔法和极大似然法。根据我们在港珠澳大桥、广州新中轴线电视塔和深圳LNG等项目的实践经验,不同的参数估计方法得到的分布参数有一定差别,从而计算得到的重现期风速也有一定的差别。有时候,对较长的重现期(如100年),计算得到的最大风速差距较大,由于工程抗风设计所需的重现期最大风速值直接影响到工程的安全性和投资造价,因此,在实际工作中如何选用合适的参数估计方法,使计算得到的结果更为合理、准确,是一个具有重要实际意义的问题。孟庆珍等应用极值Ⅰ型分布函数对成都地面年最大风速进行了概率计算,参数估计方法采用矩法和耿贝尔法,结果表明耿贝尔法效果较好[1];段忠东等比较了极值Ⅰ型分布的几种参数估计方法:矩法、耿贝尔法、极大似然法和概率权值法,结果表明,当样本容量较小时,耿贝尔法的估计结果较差[2]。那么,广东省的具体情况又是如何呢?本文应用极值Ⅰ型分布函数对广东省86个气象站的年最大风速序列进行了计算,对不同的参数估计方法进行了比较。
1 极值Ⅰ型分布函数极值Ⅰ型分布函数为:
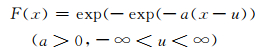
|
式中,a为分布的尺度参数,u为分布的位置参数,只要利用已有的最大风速序列x1, x2, …, xn合理估计出参数a、u的数值,则F(x)被唯一确定。
重现期为R(概率为1/R)时最大风速为:
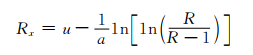
|
矩法估计在数学计算上最为简单。参数a、u与矩的关系为:
一阶矩(数学期望):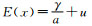
二阶矩(方差):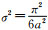
由此得到:
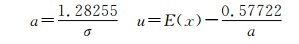
|
在实际计算中一般用有限样本容量的均值和标准差作为理论值E(x)和σ的近似估计。
2.2 耿贝尔法耿贝尔法是一种直接与经验频率相结合的参数估计方法。假定最大风速有序序列:x1≤x2≤…≤xn,则经验分布函数为:
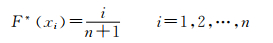
|
取如下序列:
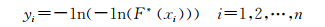
|
可得: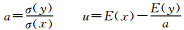
在实际计算中可用有限样本容量的均值和标准差作为E(x)和σ(x)的估计值。
2.3 极大似然法在统计学理论上,极大似然估计是一种较优的参数估计方法。极值Ⅰ型分布函数的概率密度函数为:
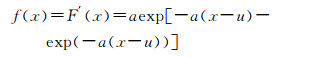
|
当观测资料x1, x2, …, xn给定时,作极大似然函数并取对数,得:
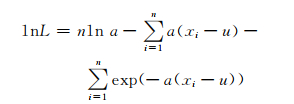
|
将a、u看作变量,将上式分别对a、u求导并令其为零,得:
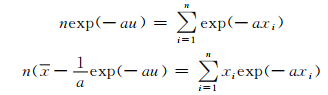
|
参数a、u可用迭代法求解。
2.4 样本序列出现特大值时参数的修改方法我国气象台站基本在1949年以后才有年最大风速的记录,至今也就50多年的资料,在不长的年最大风速序列中,有时会发生这样的现象:有一个数据特别大(特大值),按序列的大小顺序来看,很易发觉这个特大值和其它数值之间有着显著脱节的现象,例如广东省湛江站1951—2003年的年最大风速序列,样本容量为53,其中1954年的年最大风速达47.2 m·s -1,而其余52个数据中最大才是26.3 m·s-1,两者相差20.9 m·s -1,这种现象说明了这个特大值的重现期是比现有的观测年数(资料序列长度)要长得多,如果对它不加以处理,风速分布曲线的数学期望和方差均会显著提高,而使所求的风速偏高[3]。
设年最大风速序列x1, x2, …, xn,另有一特大风速xN,并估计其重现期为N年(N>n),设xn和σ2n分别表示n年资料的均值与方差,则N年资料的均值为:
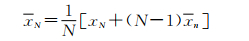
|
N年资料的方差为:
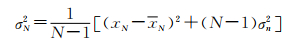
|
故出现特大值时,分布曲线参数a和u应当修改为:
(1) 矩法估计
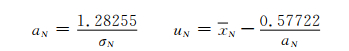
|
(2) 耿贝尔法估计
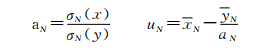
|
为了找出有效性最高的估计值和比较不同方法所求得的估计值的优良性, 计算了以下3种表征参数估计优良性的指标。
(1) 剩余方差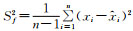
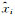
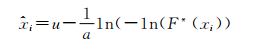
|
(2) 拟合相对偏差
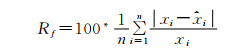
|
(3) 柯尔莫哥洛夫拟合适度检验指标
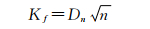
|
这里n为样本容量,Dn如下式所示:
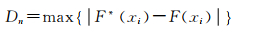
|
这里xi为有序样本,Dn表示在所有各点上,经验分布与假设的理论分布之差的最大值。取信度为0.05,查表得只要Kf<1.35,则认为年最大风速服从极值Ⅰ型分布。
显然,以上3种指标均是越小表示拟合效果越好。
3.2 不同参数估计方法的比较对广东省86个气象站1951—2003年的年最大风速序列根据其历史沿革,依据有关规范进行了次时和高度订正,统一订正为距地面10m高度的10分钟平均年最大风速,这8 6个站均匀地分布在广东省境内,测站地面海拔高度在2.5~302.8m之间,较好地代表了沿海地区、珠江三角洲平原地区以及内陆丘陵和山地的情况。
对3种表征参数估计优良性的指标Sf2、Rf、Kf的计算结果统一取3位小数,根据统计学理论,比较不同参数估计方法的优良性主要比较剩余方差Sf2,若两种方法的Sf2指标持平,则再比较Rf、Kf指标[4]。
计算结果表明,86个站中,有4个站用3种参数估计方法计算得到的Kf指标均大于1.35,即年最大风速不服从极值Ⅰ型分布;其余82个站用3种参数估计方法计算得到的Kf指标均小于1.35,即3种参数估计方法均能得到有效的分布参数,年最大风速服从极值Ⅰ型分布。
上述82个站中,有6个站出现特大值(此时实质只有矩法和耿贝尔法估计),另有6个站极大似然法无解,为便于比较,列出余下70个站3种参数估计方法的Sf2、Rf、Kf指标的平均值,矩法估计为0.518m2·s-2、4.062%和0.730,耿贝尔法估计为0.440 m2·s-2、3.616%和0.670,极大似然法估计为0.537m2·s-2、3.588%和0.676。根据上述的指标比较办法,这70个站的计算实例中,有4例以矩法估计为优,有8例以极大似然法估计为优,其余58例以耿贝尔法估计为优;在6个站极大似然法无解的计算实例中,有1例以矩法估计为优,5例以耿贝尔法估计为优;在6个出现特大值的站的计算实例中,均是耿贝尔法估计为优。因此,总体而言,耿贝尔法最优。
另一方面,上述70个站的计算实例中,有38例以矩法估计效果最差,有31例以极大似然法估计效果最差,仅有1例以耿贝尔法估计效果最差。
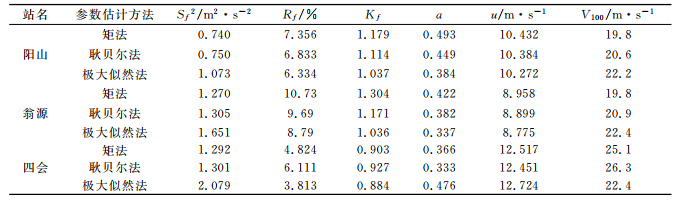
将矩法、耿贝尔法和极大似然法估计分别为优的3种情况的计算结果列于表 1、2、3,表中列出不同参数估计方法计算得到的极值Ⅰ型分布参数a、u值及其优良性指标Sf2、Rf和Kf,同时列出100年重现期的年最大风速V100。
|
|
表 1 矩法估计为优的计算实例 |
|
|
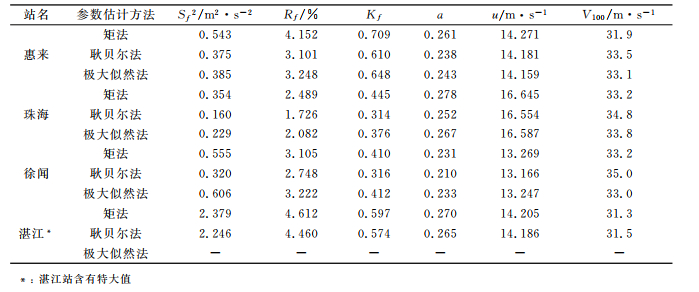
表 2 耿贝尔法估计为优的计算实例 |
|
|
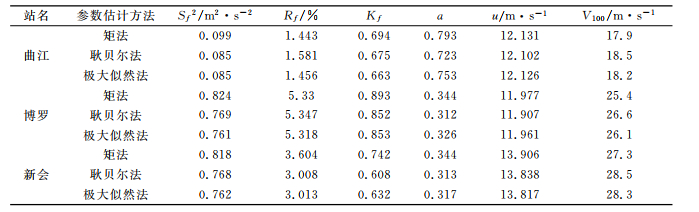
表 3 极大似然法估计为优的计算实例 |
在矩法估计为优的计算实例中,矩法和耿贝尔法的3项优良性指标较为接近,计算得到的100年重现期的年最大风速V100值也相差不大。从表 1看出,在四会站的计算实例中,矩法估计效果最好,极大似然法估计效果最差,极大似然法计算得到的V100 值比矩法小2.7m·s-1,比耿贝尔法小3.9m·s-1,虽然其Rf、Kf指标均为最小,但其Sf2指标最大,显然,有理由认为矩法估计的结果更为合理。
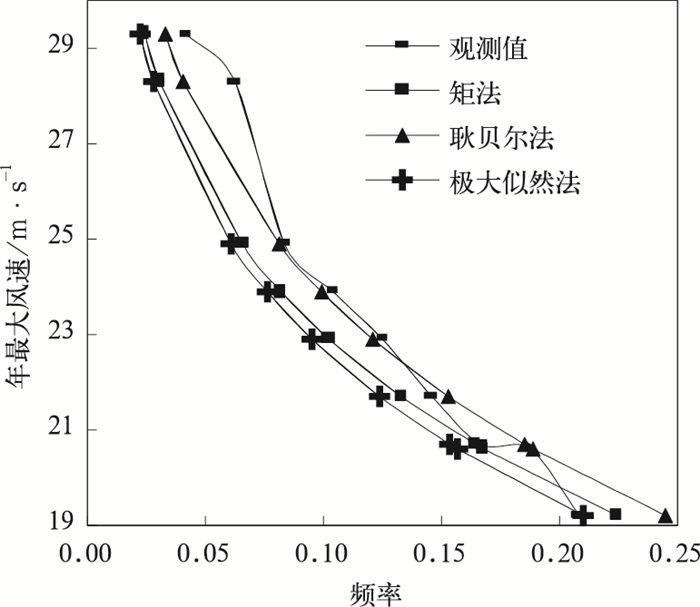
表 2为耿贝尔法估计为优的计算实例,在徐闻站的计算实例中,耿贝尔法计算得到的V100值比矩法大1.8m·s-1,比极大似然法大2.0m·s-1,但其3项优良性指标均为最小,因此,有理由认为耿贝尔法估计的结果最为合理,徐闻站的年最大风速概率分布拟合曲线如图 1所示,从图中看出,当频率较小(即极值风速较大)时,耿贝尔法的拟合曲线最接近实测曲线。在惠来站的计算实例中,矩法估计效果最差,其计算得到的V1 00值分别较耿贝尔法和极大似然法小1.6m·s-1和1.2m·s-1。在6个出现特大值的站的计算实例中,均是耿贝尔法估计为优,但其优良性指标与矩法均较为接近,计算得到的V100值均是以耿贝尔法的结果稍大一点。此外,如对湛江站的特大值不予处理,则用耿贝尔法计算得到的V100值为38.3m·s-1,而对特大值加以处理,参数修改后,V100值为31.5m·s-1,两者相差6.8m·s-1,达后者的21.6%,差距是较大的。
|
图 1 徐闻站的年最大风速概率分布拟合曲线 |
在8个极大似然法估计为优的计算实例中,极大似然法和耿贝尔法的3项优良性指标较为接近,计算得到的V100值相差很小,最大为0.7m·s-1,最小为0.1m·s-1,平均为0.3m·s-1。
表 4为仅有的1例以耿贝尔法估计效果最差的情况,从表中看出,耿贝尔法的3项优良性指标与矩法和极大似然法是较为接近的,其V100值较矩法和极大似然法大0.8m·s -1和0.7m·s-1。
|
|
表 4 耿贝尔法估计效果最差的计算实例 |
根据广东省86个气象站年最大风速序列的计算实例,极值Ⅰ型分布函数的3种常用参数估计方法中,在大多数情况下采用耿贝尔法时拟合效果最好,即使在矩法或极大似然法为优的情况下,其拟合优良性指标与耿贝尔法也较为接近,计算得到的100年重现期的年最大风速值也相差不大。因此,在广东省应用极值Ⅰ型分布函数进行极值风速的概率计算时,其参数估计方法应首选耿贝尔法。
| [1] |
孟庆珍, 唐谟智. 成都地面气温与风速年极大值的渐近分布及参数估计[J]. 成都气象学院学报, 1997, 12(4): 284-291. |
| [2] |
段忠东, 周道成. 极值概率分布参数估计方法的比较研究[J]. 哈尔滨工业大学学报, 2004, 36(12): 1605-1609. DOI:10.3321/j.issn:0367-6234.2004.12.006 |
| [3] |
广东省沿海风压研究小组. 风压问题研究及计算方法[R]. 广东, 1977: 25.
|
| [4] |
屠其璞, 王俊德, 丁裕国, 等. 气象应用概率统计学[M]. 北京: 气象出版社, 1984: 243-244.
|
| [5] |
袁春红, 薛桁, 杨振斌. 建筑风荷载风压计算中的若干问题[J]. 气象, 2002, 28(1): 39-42. DOI:10.7519/j.issn.1000-0526.2002.01.009 |
 2007, Vol. 33
2007, Vol. 33