我国是世界上气象灾害最严重的国家之一。近年来,全球气候持续变暖,各类极端天气事件更加频繁,天气气候异常变化对我国国民经济、人民生产生活的影响日益增大,造成的损失和影响不断加重,实施有效的气象风险评估和管理迫在眉睫。美国政府在其减灾计划中指出:“减灾始于风险分析。为了迎接面前的挑战,必须做出主要的政策变化:(1)预测与评估风险,而不是简单地对灾害做出反应;(2)增强风险评估以指导减灾”。《中华人民共和国减轻自然灾害报告》中制定的我国减灾十年的三个目标之一,就是“对全国自灾害进行综合评估”。国办发[2007]49号文件《国务院办公厅关于进一步加强气象灾害防御工作的意见》明确指出,要实现对各种灾害性天气气候事件的实时动态诊断分析、风险分析和预警预测,要及时开展气象灾害分析评估,做好相关科学解释和说明工作,增强公众抗御各类气象灾害的信心。而我国传统的自然灾害管理重点是危机管理,重救轻防,轻视灾前的预防和准备,其中尤其是缺乏定量风险分析的结果,凸现出综合管理力度不强。随着气象风险乃至气象灾害在全球造成的影响越来越大,人们的注意力越来越转向降低灾害风险方面,即通过采取各种减灾行动及改善运行能力的计划降低灾害事件的风险。自然成灾机制说明,在未来若干年中,人类还不可能控制灾害源和灾害载体,必须探索怎样能以最少的投入获得最大的安全保障,这些工作的基础就是进行风险评估和风险分析[1-3]。
气象风险具有自然的和社会的双重属性,是一种自然-社会现象。从风险演变成灾害,取决于风险种类、所牵涉的系统和风险发生的环境,综合考虑社会风险认知、与社会放大因素的影响,包括人类行为的决定因素,从组织因素到文化、社会因素均应考虑,其最终结果更与城市运行能力有关,当发生地区的社会经济系统的承灾能力较强,某风险事件的发生对当地未造成危害,则该高影响天气事件还是风险,暂不构成灾害。
由于作为气象风险源的高影响天气事件具有难以度量、不确定性强、多因素影响和难以归属等特性,因此对其进行风险评估仍是一个难度较大的课题,更需要加强不同学科的结合,国内专家做了相关研究工作。叶笃正等认为,天气气候预测中的不确定性是不可避免的,并根据风险经济学和决策理论,构建了一个未来天气气候预测体系的概念模型。其主要思想是将气象预测过程同用户决策过程有机地结合起来,充分利用来自用户的知识和风险管理经验,形成一个相互作用协同发展的预测体系[4]。祝燕德等提出从风险角度来认识天气气候变化,利用现代风险管理技术来加强天气风险管理,预防和减轻天气气候变化对经济建设、人们生产生活造成的负面影响,同时充分利用天气气候资源促进经济社会发展[5]。周秉荣等应用灾害学的理论和观点,以青海牧区为研究对象,对造成青藏高原雪灾的致灾因子、孕灾环境和承灾体等要素综合分析,建立从降水、积雪、成灾、灾情评价的综合判识模型[6]。
罗慧等分析了奥运期间与气象自然灾害相关的风险特点、风险分析及风险控制手段、风险相关利益主体等,并提出了高影响高敏感天气对不同比赛阈值的设定[7]。冯利华利用基于信息扩散理论的风险评估方法,对中国东南沿海各省、市、自治区的热带气旋进行了风险分析,得到地方热带气旋出现比例的风险估计值[8]。
不同于前人研究视度,本研究分析中更侧重在社会公众对不同气象风险源的关注度及其关注程度的差异上;同时认为遍及全国的12121气象信息电话拨打次数数据,具有易于获取、真实可信、连续等特点,能够客观全面反映出社会公众的需求,以及对不同风险源发生时所给予的关注。因此,本文风险评估着重强调识别和分析风险发生不确定意义下的概率,将它与12121数据联系,确定社会公众关注度等级和人数的过程。以西安市为例,挑选在2004—2006年与公众生活关系密切的7类天气事件:高温、热浪、桑拿、小雨、中雨、大到暴雨和雷暴,这些都是产生气象风险的直接风险源,以这7类风险因子发生时所对应的当天12121的日拨打量作为统计指数,利用基于模糊数学和信息扩散理论的风险评估方法,来模拟公众对各种天气事件的关注度,通过风险评估手段计算人们对不同的天气事件的关注度,可以有助于决策者以及社会公众响应相关风险时有比较定量的判断。
1 基于模糊数学的风险评估理论和方法对于高影响天气事件,属于较小样本事件(Small-Sample Problem),应用建立在大数定理基础之上的传统概率统计方法给出的概率统计结果有时就很不可靠,因此,较全面地进行气象相关灾害风险评价,可以采用模糊数学方法。信息扩散是一种对样本进行集值化的模糊数学处理方法,它为了弥补信息不足而考虑优先利用样本的模糊信息,从而对样本进行集值化,其原始形式是信息分配,最初用于地震工程领域。研究证明,应用该原理进行随机变量的概率密度估计时,估计均方误差收敛于0的速度大于在样本总体完全未知情况下经常用到的直方图估计的均方误差的收敛速度,因此将风险评估模型建立在模糊数学基础上,与应用直方图估计的方法相比,在精确度方面是一个提高。
可以将单值样本变成集值样本,最成熟的模型是正态扩散模型[9-10]。设统计指数论域为U= {u1, u2…,un},按照此式,一个单值观测样本yj可以将其所携带的信息扩散给U中的所有点:
| $ {f_j}\left( {{u_i}} \right) = \frac{1}{{h\sqrt {2\pi } }}\exp \left( { - \frac{{{{\left( {{y_j} - {u_i}} \right)}^2}}}{{2{h^2}}}} \right) $ | (1) |
式中h为扩散系数,可根据样本集合中样本的最大值b、最小值a和样本个数m来确定:
| $ h = \left\{ {\begin{array}{*{20}{c}} {1.4230\left( {b - a} \right)/\left( {m - 1} \right), m < 10} \\ {1.4208\left( {b - a} \right)/\left( {m - 1} \right), m \geqslant 10} \end{array}} \right. $ | (2) |
令:
| $ {\mu _{yj}}\left( {{u_i}} \right) = {f_j}\left( {{u_i}} \right)/{\mathit{C}_j} = {f_j}\left( {{u_i}} \right)/\sum\limits_{i = 1}^n {{f_j}\left( {{u_i}} \right)} $ | (3) |
把μyj(ui)称为样本yj的归一化信息分布,就将单值样本y变成了一个以μyj(ui)为隶属函数的模糊子集y*。对μyj(ui)进行处理,可以得到一种效果好的风险评估结果。令:
| $ q\left( {{u_i}} \right) = \sum\limits_{j = 1}^m {{\mu _{yi}}\left( {{u_i}} \right)} $ | (4) |
其物理意义是:由{y1, y2, …, ym},经信息扩散推断出,如果自然现象观测值只能取u1, u2, …,un中的一个,那么,在将yj均看作是样本代表时,观测值为ui的样本个数为q(ui)个。显然,q(ui)通常不是一个正整数,但一定是一个不小于零的数。再令:
| $ P\left( {{u_i}} \right) = q\left( {{u_i}} \right)/Q = q\left( {{u_i}} \right)/\sum\limits_{i = 1}^n {q\left( {{u_i}} \right)} $ | (5) |
事实上,Q就是各ui点上样本数的总和,P(ui)就是样本落在ui处的频率值,可以作为概率的估计值。对于自然现象统计指数X={x1, x2, …, xn},通常将X取为统计指数论域,xi取为论域U中的某一个元素ui。显然,超越ui的概率值应为式6,P(u≥ui)就是所要求的风险估计值。
| $ P\left( {u \geqslant {u_i}} \right) = \sum\limits_{k = 1}^n {P\left( {{u_k}} \right)} $ | (6) |
结合西安市的实际情况,选择影响公众生活天气事件,主要选取2004—2006三年的高温、热浪、桑拿、小雨、中雨、大到暴雨和雷暴等7类天气为研究对象,这些都作为产生气象相关风险的风险源。其定义基本上按照气象部门的定义,并参照了当地的实际情况:高温指当天最高气温大于等于35℃;高温持续3天及以上为热浪;桑拿天是最高气温大于等于32℃,且最低相对湿度大于等于50%;大到暴雨是24小时降水量大于等于25.0mm;中雨是24小时降水量大于等于10.0mm小于24.9mm;小雨是24小时降水量大于等于0.0mm小于9.9mm。
2.2 收集逐日12121气象电话拨打量数据找出2004—2006年气象电话12121的逐日拨打量数据,单位均为次数。从图 1可以看出3年间西安市12121气象咨询电话拨打量的分布,日拨打量最大峰值不超过10万次。

|
图 1 2004—2006年西安市气象咨询电话拨打量分布图 |
以高温天气为例,在给定的时间段内,共有89个样本,每一个样本有与其相对应的12121电话拨打量数据,收集汇总此数据作为研究的样本量;其余天气事件依此类推。3年中各类高影响天气事件为:89个高温样本,14个桑拿天样本,43个热浪样本,30个雷暴样本,12个大到暴雨样本,30个中雨样本,202个小雨样本量。
2.4 按照信息扩散的方法计算每一类天气的拨打量对应7种高影响天气事件和当地气象信息电话实际情况,确定连续论域μ为[0, 80000]。计算得到该类天气事件的风险概率估计值,可以反映人们对这种高影响天气事件的关注程度,这代表了不确定意义下的气象风险估计。
3 计算结果依据上述思路,把一维实数空间上的集合[0, 80000]作为的xi论域,将连续论域[0, 80000]按等间距取点,转变为离散论域,根据式(1)~(6)计算,可得公众对5类高影响天气事件风险估计值,首先以高温天气事件为例进行计算。
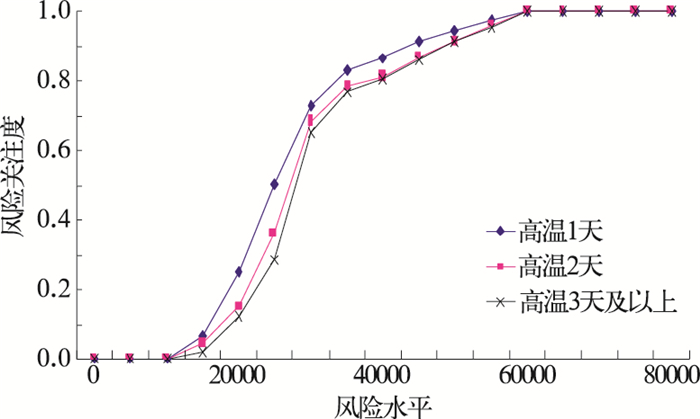
3.1 高温不同持续天数的风险关注度以高温天气为例,2004—2006年共有高温天气事件89个,持续出现2天61个、持续出现3天及以上43个。设yi=(j=1, 2, …,89)为历次高温事件。根据风险水平的变化范围,把一维实数空间上的集合[0, 80000]作为xi的论域。将连续论域[0, 80000]按等间距取点,转变为离散论域,表征不同的风险水平。考虑到计算精度的要求,取17个控制点(n=17),构成离散论域:U={u1, u2, …,un}={0,5000,10000,…,80000},此时样本个数m=89,样本最大值b=55655,最小值a=11308,根据公式(2)可得扩散系数h=716.0025。根据公式(1)~(6)计算,可以得出高温天气事件发生时的超越概率风险估计值P。由于高关注度下电话拨打量大,风险水平高,危险概率大,为了便于理解,转为计算1-P作为关注风险的累积概率值,来表征不同风险水平下的风险关注度(详表略)。进而可以得到高温持续天数的风险关注度分布图(见图 2),可以看出,在不同的风险关注度(纵坐标),社会公众对高温天气关注的风险水平(横坐标),随高温持续天数的增加而增加。
|
图 2 高温不同持续天数的风险关注度分布 |
方法同上,可以算出热浪、桑拿、小雨、中雨、大到暴雨、雷暴等其余6种高影响天气事件的风险超越概率、风险关注度和关注度风险水平。根据西安市电话拨打实际情况,将7类风险源最低拨打量从0至20000划分为一般风险水平关注度;将7类风险源最低拨打量从25000至40000划分为中风险水平关注度;拨打量45000及以上划分为高风险水平关注度。根据这种分类方法,计算得到表 1,即社会公众对高影响天气事件风险关注度和关注度风险水平。
|
|
表 1 社会公众对高影响天气事件风险关注度和关注度风险水平 |
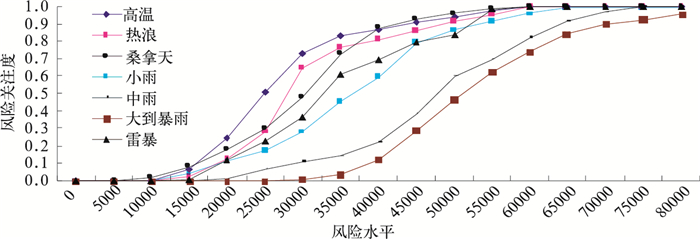
根据表 1,可以得到公众对不同高影响天气事件的风险水平关注度的概率分布曲线(详见图 3),可以看出,在不同的风险关注度,公众对不同高影响天气关注的风险水平,从低到高依次为高温、热浪、桑拿天、雷暴、小雨、中雨和大到暴雨。
|
图 3 公众对不同高影响天气事件的风险水平关注度分布 |
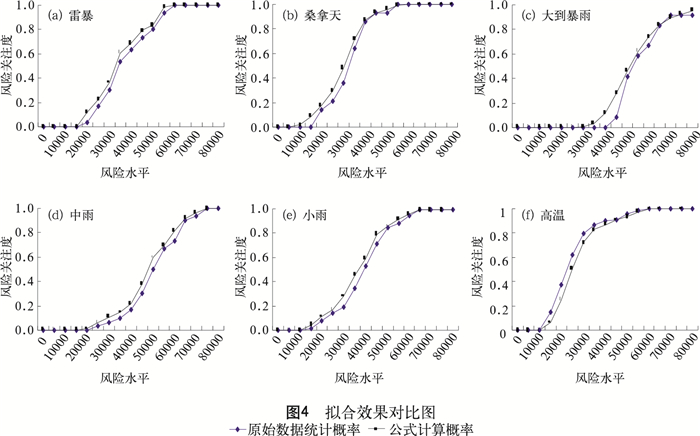
为了验证本文所提出模型和公式的正确性,根据文章中“风险超越概论”及“风险关注度”的概念对已有的原始数据进行计算处理,所得结果与根据公式所得结果进行对比,进而验证公式的可信程度。以高温的89个原始数据为例,其具体的实施步骤如下:首先,按论域进行分档次处理,统计各档次出现的次数,计算其出现概率;其次,根据定义,用公式求得其风险关注度;最后,将两者计算所得数据进行拟合效果比较,两条曲线拟合得较好,其余风险源同理,发现7类曲线均拟合得较好(详见图 4,热浪图略),验证了本文所提出的思路和公式可信程度较好。
|
图 4 拟合效果对比图
 原始数据统计概率 原始数据统计概率  公式计算概率 公式计算概率
|
(1) 利用模糊数学和基于信息扩散理论的风险评估方法,以高影响天气事件作为重要气象风险源,综合应用气象热线电话拨打量信息,通过计算超越概率,计算社会公众对不同高影响天气事件的风险关注度,得出不同级别关注度风险水平,进而计算得出关注人数,经初步检验,拟合效果较好。
由于全国气象部门均在积极开展12121气象信息服务电话的工作,12121拨打次数具有易于获取、真实可信、连续等特点,是反映社会公众需求的客观而有价值的信息,因此推广此分析方法,简单易行,与通过城市社会调查工作获取相关信息相比,成本廉价。
(2) 研究发现:第一,西安社会公众对不同风险关注度有明显差异,在不同的风险关注度,公众对不同高影响天气关注的风险水平,从低到高依次为高温、热浪、桑拿天、雷暴、小雨、中雨和大到暴雨;第二,即便是在夏季,社会公众对普通降水和雷暴天气的关注度风险水平要高于对高温热浪和桑拿天气的关注度风险水平。究其原因:夏季降水多是局地性阵性降水,其降水起始时间、持续强度和时间往往是突发性的,不易采取防范措施,较大地影响了人们的生产生活,因此引起社会公众较高的关注度风险水平;而高温类天气一般发生的时间主要集中在仲夏,酷热属于自然规律,再加上其发生过程和持续时间是缓慢累积性的,人们逐渐具有心理准备,因此社会公众对此类事件的关注度风险水平略低;第三,社会公众对高温天气事件关注的风险水平随着高温持续天数增加而增加。
(3) 应用风险评估和分析计算结果,通过公共气象服务平台发布以人为本的风险关注度和风险水平等级,有利于提醒社会公众关注高影响乃至灾害性天气气候事件,关注其对日常生活、生产、交通运输和旅游的影响,提高对各种气象风险的防灾减灾意识并及时采取防范应对措施,从而达到预防和减轻高影响天气事件所造成负面影响的目的。
(4) 分析结果可以作为判断气象影响力的定量结果,为政府部门向气象部门投入提供有价值的参考依据。公众对降水类风险源的关注度风险水平更高,决策部门就要及早制定针对降水类风险源可能会演变成沥涝、内涝、洪涝等灾害、并可能引发次生衍生灾害的城市运行保障的应对措施和应急预案。
| [1] |
U. S. Government Printing Office, Natural Disaster Reduction, A Plan for the Nation, 1997.
|
| [2] |
刘新立. 区域水灾风险的相关分析与因子分析——以湖南省为例[J]. 经济科学, 2004(2): 94-101. |
| [3] |
张继权, 冈田宪夫, 多多纳裕一. 综合自然灾害风险管理—全面整合的模式与中国的战略选择[J]. 自然灾害学报, 2006, 15(1): 29-37. |
| [4] |
叶笃正, 严中伟, 戴新刚, 等. 未来的天气气候预测体系[J]. 气象, 2006, 32(4): 3-8. DOI:10.7519/j.issn.1000-0526.2006.04.001 |
| [5] |
祝燕德, 胡爱军, 熊一鹏, 等. 经济发展与天气风险管理[M]. 北京: 中国财政经济出版社, 2006.
|
| [6] |
周秉荣, 申双和, 李凤霞. 青海高原牧区雪灾综合预警评估模型研究[J]. 气象, 2006, 32(9): 106-110. DOI:10.7519/j.issn.1000-0526.2006.09.018 |
| [7] |
罗慧. 奥运气象服务综合风险管理及评估研究[J]. 气象软科学, 2006(3): 79-86. |
| [8] |
冯利华. 热带气旋风险评估[J]. 海洋通报, 1999, 18(2): 40-43. |
| [9] |
Huang Chongfu. Principle of information diffusion[J]. Fuzzy Sets and Systems, 1997, 91: 69-90. DOI:10.1016/S0165-0114(96)00257-6 |
| [10] |
黄崇福. 自然灾害风险评价理论与实践[M]. 2006(第一版). 北京: 科学出版社: 2-45.
|
 2007, Vol. 33
2007, Vol. 33