2. 广西气象减灾研究所
2. Guangxi Meteorological Disaster Mitigation Institute
前汛期广西北部锋面暴雨是造成广西洪灾的一个重要原因,频繁的冷空气活动和南方暖湿气流的活跃,是造成广西北部降雨特多的一种可能机制。从地形看,广西北部山区山势陡峻且连绵不断,形成天然屏障。每年4-6月来自孟加拉湾的暖湿气流源源不断地从海洋输入大陆腹地,气流在广西北部山区抬升,形成暴雨。广西北部区域是广西雨量高值中心之一,也是前汛期易出现洪涝灾害的地区之一[1]。“ 94.6”.“ 98.6”和“05.6”等西江流域特大洪涝灾害给广西造成了巨大的经济损失[2, 3]。国内许多气象工作者对华南前汛期暴雨洪涝灾害频发问题进行了研究。王叶红[4]用有限区域数值预报模式(AREM)进行数值模拟,研究了华南地区的强对流系统与暴雨的关系。孙晶[5]利用MM5中尺度数值模式对“98.6"华南暴雨进行了数值模拟,用Reisner霰方案模拟了可分辨尺度降水,详细分析了暴雨的微物理过程。大多研究是对单次暴雨过程进行模拟分析,未见对广西北部区域平均降水量的逐日预报研究。本文针对前汛期广西北部地区易出现特大降水及洪涝灾害频发的特点,尝试采用条件数选择预报因子的方法,建立广西北部区域平均降水量客观预报的新方法, 为防洪减灾及面雨量估计提供可靠的预报参考依据。
1 条件数计算原理与方法线性回归分析是研究自变量与因变量之间相关关系的强有力工具,可以建立自变量与因变量的定量预报模型。线性回归方法具有客观、简便、通用性好等的特点,因而在各个学科均得到了广泛的应用。在大气科学领域的各个方面,回归方法是应用较为普遍的方法之一,也是基层气象台站最常用的预报建模方法之一[6-8]。但是,采用线性回归模型建立的回归预报模型,因自变量之间存在相关性,可能会増加参数估计的方差,使得回归方程变得不稳定,这就是我们常常提到的共线性。共线性的存在可能会导致回归系数的符号与实际不符,回归系数的估计值与实际相关太大;回归系数的标准误差太大,因而有些重要变量选不进方程。建立一个好的回归模型,一般要求自变量少而精,避免共线性对回归方程的影响。这就要求在建立多元线性回归方程时,必须对自变量之间是否存在共线性进行诊断,根据诊断结果选用合理的预报因子建立回归模型。诊断共线性影响大小较方便有效的办法是计算因子矩阵的条件数[9]。
假设有p个自变量的线性回归模型为:
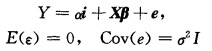
|
(1) |
其中Y为n×1的观测量,X为n×p的设计矩阵并假定己中心标准化,a为常数项,β为p×1的回归系数向量,e为n×1的随机误差向量,i为n×1的列向量。于是β的最小二乘估计为b= (XTX)-1XTY。若记λ1>λ2>…>λp>0为X´X的特征根,φ1,φ2,…,φp为其特征向量。如果X´X至少有一个特征根非常小,即非常接近于0,则称设计阵X呈病态;若有p-r个特征根接近于0则p-r个复共线性关系为:
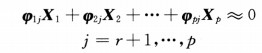
|
(2) |
其中φij为第j个特征向量φJ的分量,XJ为X的列向量。则
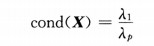
|
(3) |
cond(X)称为X´X的条件数。条件数最初应用于计算数学,它被用来描述算法的稳定性[10]。解决类似:己知d和d´,求f(d)和f(d´)之间是否接近,以及接近的情况的问题。由条件数的定义可以看出条件数是一个大于或等于1的正数,条件数小的矩阵称为“良性”矩阵,反之称为“病态”矩阵。显然一个奇异矩阵的条件数为无穷大,正交或酉矩阵的条件数为1。若条件数虽然不是无穷大,但当它很大时,就称矩阵是接近奇异的,这意味着:在这种情况下矩阵的行向量或列向量的独立性很弱。一般来说,在应用经验中,当cond(X)<100时,认为X有微弱多重共线性,当100<cond(X)<1000时,认为存在中等强度或较强强度的多重共线性,而当cond(X)>1000时认为有严重的多重共线性。
根据条件数的定义,通过计算回归方程因子矩阵的条件数,可以有效地定量诊断出回归方程的因子间是否存在多重共线性及其严重性。本文采用条件数作为判断标准,改进回归方程选择因子的方法,并对其进行区域降水量预报应用试验研究。
2 区域降水的条件数计算预报方法 2.1 资料与方法根据柳江、桂江的集水范围和预报经验,以广西境内24°N以北的站点作为预报区(见图 1),将预报区内所有站点(41个站)的逐日24小时平均降水量作为预报对象进行研究。图 1中阴影区为本文选定的预报区,基本覆盖了柳江、桂江的集水范围,正确预报区域平均降水量对防洪减灾有重要意义。
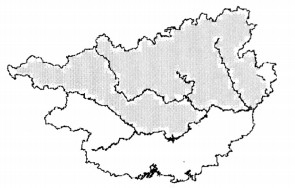
|
图 1 广西主要河流及预报区示意图 |
本文以中国气象局T213和日本数值天气预报模式的数值预报产品为基本资料,进行广西北部前汛期(5—6月)24小时平均降水量的逐日预报研究。所选用的数值预报产品包括:T213模式各标准层17个常规气象要素及物理量要素场(15~30°N、100~120°E,1°×1°,共336个格点)和日本细网格模式降水预报场(15~30°N、100~120°E,1.25°X1.25°,共221个格点)。通过对2002年、2003年5—6月逐日数值预报产品场与预报对象进行场相关普查,将成片稳定(置信水平高于0.05)的高相关格点作为预报因子的选择区,在区内选2个相邻格点的最大平均值作为待选因子。并以达到或超过0.01置信度水平作为选择预报因子的标准,最终得到36个预报因子(35个T213模式预报场因子和1个日本细网格降水预报因子)。在这初步选定的36个预报因子中,日本细网格降水预报因子的相关系数为0.6743,而35个T213模式预报因子的相关系数在0.35~0.50之间。以下方法的讨论均基于这些预选的因子。
2.2 区域平均降水量的条件数因子预报方程根据2.1节对预报因子选取结果可知,初步选定的36个预报因子中,有35个T213模式预报场因子,仅有1个日本细网格模式降水预报因子。但从相关系数看,该因子与预报对象的相关系数大于所有T213因子,说明该因子虽然在因子矩阵中的数量少,但对于所选取的预报对象来说,其与预报对象具有更好的线性相关关系,对预报对象具有更重要的指示意义,因此首先选取日本细网格模式降水预报因子作为预报方程的第1个因子。
选定日本细网格模式降水预报作为第1个预报因子后,再计算其余35个T213预报因子组成的矩阵条件数,条件数按由小到大的顺序排序。当条件数为5时,共有4个因子进入方程:X3、X4、X2、X14,其中X3是850hPa散度,X4是700hPa相对湿度,X2是200hPa散度,X14是500hPa相对湿度。用这4个根据条件数的计算选出的因子与己经入选的重要因子——日本细网络模式降水预报因子一起构成建立预报方程的因子。利用这5个预报因子,剔除数值预报产品资料不齐的日期,以2002—2003年5、6月资料为建模样本(114天),建立广西北部区域平均降水量的逐步回归预报方程:

|
(4) |
采用方程(4)对2004、2005年5、6月广西北部区域平均降水量进行业务应用预报试验,剔除数值预报产品资料不齐,不能进行预报试验的日期外,共进行了104天的试预报运行。试验的预报平均绝对误差值为6.3569mm。
2.3 区域平均降水量的逐步回归预报方程为了考查用条件数计算选取自变量的方法所建立的预报方程的预报效果,再进一步用建立方程(4)时相同的建模样本(114天)和资料,采用较易实现且预报效果较为客观的传统逐步回归法建立回归预报方程。为了便于对比分析,新建立的回归方程因子数和方程(4)一样,也是5个。当F值取8.0时,入选回归因子有5个,分别是日本细网格降水预报场因子XJP、500hPa水汽通量散度场因子X7、700hPa温度平流场因子X18、700hPa润度场X29和850hPa垂直速度场因子X34。所建立的传统逐步回归预报方程为:
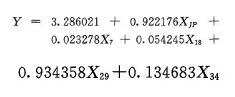
|
(5) |
采用与方程(4)相同的检验方法,用方程(5)对2004、2005年5、6月广西北部区域平均降水量进行业务应用预报试验,同样进行了104天的业务预报试运行。方程(5)的试验预报平均绝对误差为7.0096mm。
3 两种预报方程的预报效果对比分析由于预报方程(4)和(5)的建模样本长度相同,因子数相同,预报对象相同,试验预报的时段相同,因此预报效果具有较大的可比性。从两个回归方程所进行的104天业务预报平均绝对误差对比来看,方程(4)的误差6.3569mm小于方程(5)的误差7.0096mm, 本文采用的条件数计算选取预报因子的方法比传统的回归方法预报绝对误差减小了0.6527mm, 预报精度提高了9.3%,预报效果比传统的逐步回归方法有了改进和提高。在基本相同的条件下所建立的两个回归预报方程预报效果不同,这可能是因为方程所选因子间的复相关系数不同,影响了方程的预报效果。因此根据条件数的定义及其意义,可以通过计算回归方程因子矩阵的条件数考查方程所选因子间的复共线性关系。预报方程(4)所含5个因子的条件数为34.94799,逐步回归方程(5)的5个因子的条件数为1699.5567。方程(4)的条件数34.94799<100,根据一般的条件数经验可知,方程(4)的因子间存在微弱的复共线性,对方程的预报效果影响不大。但方程(5)的条件数1699.5567>1000, 说明因子间存在严重的复共线性。从预报效果看,方程(5)因子间的复共线性影响了方程的预报效果,预报误差増加。
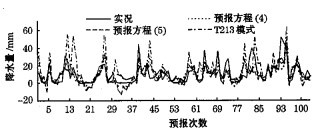
将广西北部区域内T213模式所有格点的降水预报平均值,作为T213模式对该区域平均降水量的预报值。2004年、2005年5月和6月,两个方程的广西北部区域的平均降水量的逐日预报结果和T213模式的预报结果见图 2其中实线代表实况,短虚线为方程(4)的预报,长虚线为方程(5)的预报,点划线为T213模式的预报。计算T213模式104天的绝对平均预报误差为7.9456mm。应用逐步回归法对数值预报产品进行释用,可以将绝对平均预报误差减少0.936mm, 而采用本文所提出的条件数计算选取回归因子的方法对数值预报产品进行释用,则绝对平均误差可以减小1.5887mm, 预报精度比T213提高20%。
|
图 2 2004-2005年5、6月逐步回归法、改进的条件数法及T213模式预报 |
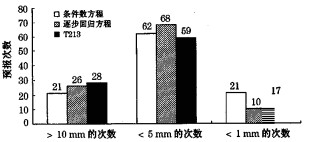
进一步深入分析三种预报结果的绝对误差,统计三种方法的预报绝对误差落在不同误差范围内的次数,结果详见图 3。由图 3可知,预报绝对误差大于10mm的次数,条件数选取预报因子法、传统逐步回归法和T213模式预报分别是21、26和28次,其中条件数选取预报因子法的预报误差大于10mm的次数是三种方法中最少的。而预报绝对误差小于1mm的次数,方程(4)的次数最多为21次,方程(5)最少为10次,T213模式为17次,说明方程(4)预报准确的次数最多,是三种方法中最为可靠的预报参考。
|
图 3 2004年、2005年5-6月三种预报方法的误差比较 |
通过对条件数计算选取预报因子方法、传统的逐步回归法和T213模式在2004年5、6月对广西北部区域平均降水量的预报结果进行对比分析可知,本文提出的通过计算条件数选取预报因子的方法比传统的逐步回归法和T213模式预报误差小,预报精度较两种方法都有所提高。本文所采用的方法具有简便易行、预报效果较好的优点,具有较好的业务应用前景。
4 小结本文针对广西北部区域前汛期易发生洪涝灾害,防灾减灾任务重,区域降水预报服务具有重要意义的问题,根据条件数原理,采用条件数计算选取预报因子的方法,建立广西北部区域平均降水量的回归预报方程。通过2004年、2005年两年5、6月的业务预报试应用,结果表明通过条件数计算选择预报因子的方法比传统的逐步回归预报方法和T213模式预报误差小,并且,采用新方法建立的预报方程的预报性能提高,其原因也是十分清楚的,即通过条件数计算选择的预报因子之间的复共线性关系明显减小,从而使建立的预报方程具有更高的预报精度,这种新的预报方法可以为广西北部区域前汛期预报服务提供更可靠参考依据。
| [1] |
罗锦珠, 黄联峰. 广西北部地区"85·5"特大暴雨洪水分析[J]. 水文, 2003, 23(1): 57-62. |
| [2] |
黄伟民, 杜文印, 钟红伟. 西江"94.6"、"98.6"、"05.6"暴雨洪水比较分析[J]. 水科学与工程技术, 2005(增刊): 30-33. |
| [3] |
孙建华, 赵思雄. 一次罕见的华南大暴雨过程的诊断与数值模拟研究[J]. 大气科学, 2000, 24(3): 381-392. |
| [4] |
王叶红, 王志斌. AREM模式对2002年汛期降水的实时预报试验[J]. 气象, 2004, 31(2): 17-22. DOI:10.7519/j.issn.1000-0526.2004.02.004 |
| [5] |
孙晶, 王鹏云. 用MM5模式Reisner霰方案对华南暴雨数值模拟[J]. 气象, 2002, 29(4): 10-14. |
| [6] |
郑海青. 福建省森林火险中期预报方法[J]. 气象, 2002, 29(7): 56-57. |
| [7] |
邓水, 李坚辉. 影响湛江的热带气旋自回归分析和预报[J]. 海洋通报, 2000, 19(2): 90-92. |
| [8] |
杨松, 杞明辉, 姚德宽. 误差订正在预报集成中的应用研究[J]. 气象, 2002, 29(12): 22-25. |
| [9] |
刘准, 陈哲. 条件数在系统可观测性分析中的应用研究[J]. 系统仿真学报, 2004, 16(7): 1552-1555. |
| [10] |
祝新民, 畅建海, 李济生, 等. 克服复共线性影响的方法探讨[J]. 飞行器测控学报, 2003, 22(2): 7-11. |
 2006, Vol. 32
2006, Vol. 32