雷电过程通常总是跟强对流天气和雷暴降雨过程联系在一起, 雷暴的起电和闪电研究是当今关于风暴研究的一个重要方面, 闪电定位和特征测量对于全面、深入地研究强风暴过程至关重要[1]。而在闪电特征量中, 地闪回击电流是雷电防护技术中的一个重要参数[2], 准确获取雷电流大小以及波形对于采取正确的雷电防护措施、保护人民生命财产是非常重要的。在我国, 由于开展雷电研究的时间较短, 到目前为止还没有详细的雷电流波形资料, 因此了解雷电流测量技术和方法及其观测结果对雷电防护技术的发展具有重要作用。目前地闪回击电流实验数据的获取方法大致可以分为以下三类:(1)利用塔的测量:由于高塔被雷电击中的几率相对更大, 可在其上安装雷电流测量设备进行观测。(2)人工触发闪电观测:因为人工触发的闪电可以预知其发生的时间和地点, 且继后回击与自然闪电的相类似, 所以可以利用人工触发闪电直接测量雷电回击流。(3)间接估测:通过远距离电磁场的测量来估测地闪回击电流数据。以上这些观测结果为雷电物理研究和雷电防护设计提供了大量可靠的数据源, 也为建立更完善的雷电防护标准提供了科学依据。
1 雷电流的直接测量雷电流的直接测量包括对自然闪电和人工引雷电流的测量。一般的自然闪电是由下行梯级先导开始的, 存在首次回击的过程; 而人工引雷则以上行先导开始, 其后是一连续电流过程, 没有自然闪电中的首次回击。但人工引雷和自然闪电都有继后回击及之后的连续电流过程[3]。仅从电流有关的特征量来看, 自然闪电和人工引雷在继后回击的过程中是相似的。Uman等人[4]总结了众多观测结果后看到, 如果将自然闪电和人工引雷的继后回击所产生的电场变化峰值归一化到100km处, 其值不存在明显的差异。这说明从电流角度来看人工引雷是可以比较好的反映自然闪电在继后回击过程中的特征。
1.1 矮塔测量Berger等[5]利用矮塔上安装的雷电流测量设备对闪电通道底部的地闪回击电流数据进行了较为全面的观测。观测所在的塔高度分别为70m和90m。塔位于Lugano的San Salvatore山, 山顶海拔高度为914m, 高出位于山脚的Lugano湖水面640m。他们利用安装在塔顶的同轴分流器对闪电电流进行了测量。测量结果发现大约有15 %的地闪由下行梯级先导引发, 大多数打到高塔上的雷电都是首先由正、负两种极性的上行梯级先导所引起。负地闪首次回击和正地闪首次回击电流峰值的中值约为30kA, 负地闪继后回击电流峰值的中值约为12kA。
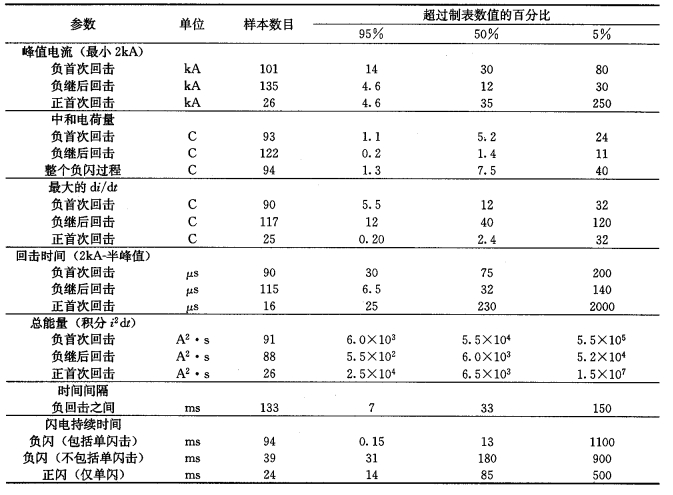
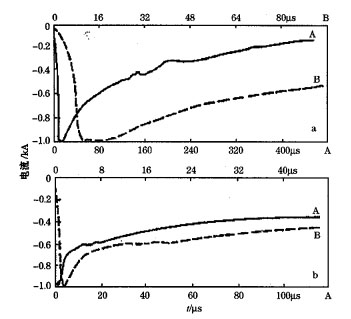
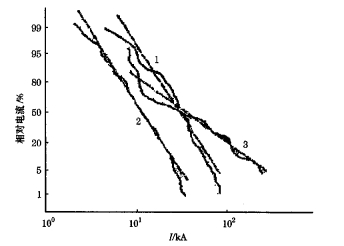
图 1和图 2是Berger [5]等人所观测到的由下行先导激发的地闪回击电流波形和峰值分布。由于受所用仪器设备带宽的限制, 同时观测数据可能受到建筑结构的影响而偏大, 因而他们所测的电流最大上升率数据的可信度存在一定的争议。表 1列出了观测中所获得的一些闪电参数。
|
图 1 典型的负回击电流波长
(a)首次回击; (b)继后回击 实线和虚线分别为对同一个波形在不同时间尺度上的描绘。横坐标为时间, 纵坐标为电流的相对振幅 |
|
图 2 地闪回击电流峰值的统计分布 1.负地闪首次回击; 2.负地闪继后回击; 3.正地闪横坐标为电流强度, 纵坐标为相对电流所占百分比 |
|
|
表 1 下行闪电的电流参数[5] |
而Eriksson等[8]于1970年代在南非一块相对平坦地区的一座60m高的塔上进行的闪电电流测量实验结果却稍有不同。他们发现在观测到的闪电中有超过50 %的闪电是由常见的下行梯级先导引发的。但实验中没有观测到正地闪, 因而下行梯级先导大多为负极性的。而在这次实验中发现的快速的电流上升时间在当时其他研究中是未曾观测到的。他们还发现有95 %的继后回击电流峰值超过了4. 9kA, 50 %的继后回击电流峰超过了12kA, 还有5 %的继后回击电流超过了29kA。
Garbagnati [5]和Dellera等[7]于1970年代在Italy北部和中部进行的观测表明, 下行闪电的首次回击电流峰值约为33kA, 继后回击的峰值电流约为18kA。
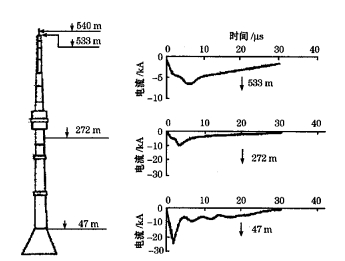
1.2 高塔测量首次在三个不同高度上对闪电回击电流进行同步测量的实验是在Moscow 540m高的Ostankino塔上进行的。三个电流感应器分别安装在距地面533m、272m和47m高度处[8]。图 3是一次测量的结果。从图 3中可见闪电回击电流在三个不同高度上表现出不同的波形。在三个波形中最大的电流峰值(大约22kA)出现在较低的观测位置(47m), 而533m处测到的8kA的电流峰值要小于272m处测到的10kA的电流峰值, 这表明在塔底和地面阻抗之间的不连续点上, 有一个正的电流反射进入了初始回击电流中, 这个正反射在几个微妙后, 在其它两个观测点上也清楚反映出来了。但由于塔顶产生了一个负的反射电流, 使得272m高度的电流峰值比533m高度处的电流峰值大。Rakov在47m和533m分别测量到了18kA和9kA的中等强度的电流峰值, 并提出塔的有效接地电阻要远小于它本身的特性阻抗, 也比闪电通道的等效电阻略低一些[9]。
|
图 3 Moscow的Ostankino塔上三个不同位置测量到的上行负闪回击电流波形个例 |
另外, 加拿大的CN电视塔闪电研究组(CNTLSG)早在1978年就开始利用安装在多伦多的CN电视塔上509m和474m高度处的Rogowski感应线圈来测量闪电电流变化率, 其观测结果与Ostankino塔上得到的结果一致, 即在塔的不连续处出现了成倍的反射。在与地面连接处表现出正的反射, 而在塔顶则为负。所不同的是, CN电视塔展示的电流波形比Ostankino塔更为复杂[7-9], 并证实了Shostak [12]指出的导致电流不连续性的原因。
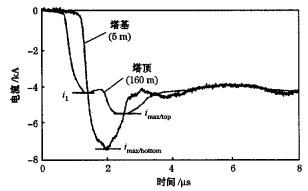
图 4是在德国Peissenberg塔上观测到的一次回击波形的比较。探测器分别安装在了塔的167m和13m处。从图中可以很明显的看到, 对于同一次回击, 由于塔顶和塔底对电流的反射, 在塔的不同位置所观测到的电流峰值的大小和时间都有着显著的差异。
|
图 4 Peissenberg塔顶部和底部所观测到的闪电回击电流波形 |
人工引雷指在雷暴电环境下利用一定的装置和设施, 人为在某一指定地点触发的闪电[3]。目前人工引雷主要是利用火箭-导线技术来实现的。当所用导线直接接地时引发的雷电类似于地面高建筑物激发的上行雷。近年来出现的“高度引雷技术”则在导线和大地之间使用一根较长的尼龙线从而使导线大地绝缘。这样做的目的是为了模拟自然雷电中的下行梯级先导。尼龙线越长越可以真实的模拟下行梯级先导[3]。在雷暴云下为正环境电场的情况下, 人工引发雷电一般在初始连续电流过程之后即行终止, 放电的峰值电流一般在千安上下; 但在雷暴云下为负环境电场的情况下, 初始连续电流过程之后, 常常会发生数次直窜先导及继后回击过程, 放电的峰值电流可达数十千安, 放电持续时间一般在数百毫秒甚至一秒以上。这些继后过程和自然闪电的同类过程是完全相似的。
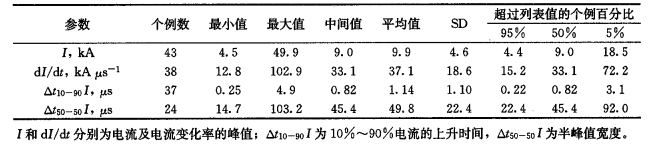
表 2为1990年在法国进行的人工引雷实验所获得的闪电参数[14]。
|
|
表 2 1990年法国人工引雷实验回击参数 |
在人工引雷测量雷电流的感应器主要有两种:一种是利用无感抗电阻, 也叫同轴分流器作感应器; 另一种是用Rogowski线圈作感应器。通常在电流记录装置与感应器之间用光纤相连接。这样可以使记录装置与感应器绝缘, 从而使记录装置不受雷电放电过程中产生的高电压的影响。
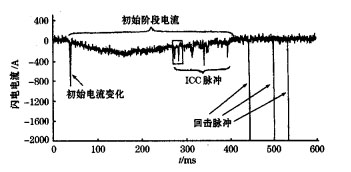
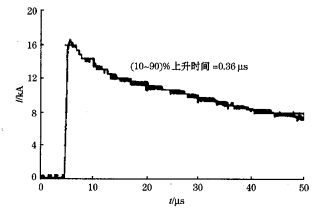
图 5为一个典型的负极性人工引雷的电流波形。与自然闪电所不同的是在人工引发雷电的初始阶段具有较长时间的初始连续电流, 对于不同的人工引雷, 初始阶段电流的持续时间、大小及所中和的电荷量都有很大差别。图 6是一次负极性人工引雷回击电流波形。实验表明, 虽然回击电流的波形类似, 但每次回击的电流峰值、10 %~ 90 %的上升时间、半峰值时间等参数存在一定的差异。人工引雷回击电流波形上升时间很快, 0 %~ 90 %的上升时间一般在1μs以下, 但同时下降也很快, 半峰椎时间很短, 一般在十几个微秒。根据统计结果发现电流变化率与电流峰值一般是成正比的关系。
|
图 5 一次典型负极性人工引雷电流 1996年6月24日17 :04 :56EDT (美国东部夏季时) Camp Blauding, Florida |
|
图 6 典型负极性人工引雷回击电流波型 |
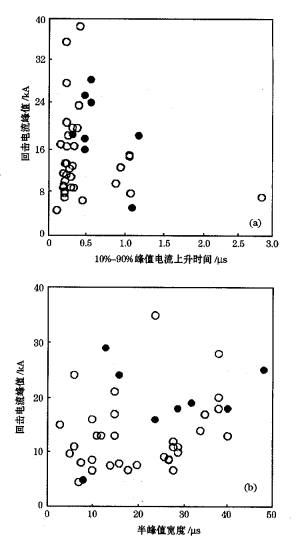
Fisher等[16]在研究了回击电流的几个参数的关系后给出了图 7。他们发现在10 % ~ 90 %的电流平均变化率与电流峰值I之间, 以及30 %~ 90 %的电流变化率与电流峰值I之间都有一个强的正相关, 相关系数分别为r=0. 71和r=0. 74。Anderson和Eriksson[17]从发生在瑞士的自然闪电中也发现了一个平均变化率对数与电流峰值之间的弱相关。
|
图 7 各种回击参数的离散点 实心点为1990年Florida KSC的数据; 空心点为1991年Alabama州Fort McClellan的数据 (a)电流峰值与10%~ 90%上升时间的关系; (b)电流峰值与半峰值时间的关系 |
而Crawford则从1997年在Camp Blanding做的一次人工引雷实验中得到回击电流峰值的对数与10 %~ 90 %上升时间之间相关系数0. 8 [18]。
2 雷电流数据的间接测量对雷电流数据的间接测量主要是利用远距离电磁场和电流的关系, 从遥测的电场或磁场得到的数据, 反演得到回击电流峰值。闪电定位系统除了能够提供闪电时间和回击点位置之外, 还可以利用一定的回击模式反演得到闪电回击电流峰值。如果能够获得远距离电磁场测量和闪电电流的可靠关系, 这些系统将可以为雷电防护标准的制定提供可靠的数据。而且, 这种方法简便易行, 适应于更广泛的地理环境, 同时也可以避免人工引发闪电和高塔测量中的不利影响。目前大量闪电定位系统的广泛布设和应用, 为获取这些数据提供了条件, 但大量因素限制了这些估测结果的准确性。对于单个放电过程最小的误差也达20 %~ 30 % [19]。由于未知参数影响, 例如闪电回击速度, 或由于雷击物的影响而产生的电流反射(如雷击高建筑物), 使得由远距离电磁场反演闪电回击电流参数存在着一个固有的困难[20, 21]。
2.1 基于闪电实验数据得到的经验公式例如Rakov等[22]利用28个人工引雷的实验资料, 由回击电流、两个距离上的回击速度和电场测量, 提出了如下回击电流峰值I与距离闪电D处的电场峰值E的回归公式:

|
(1) |
这里的I单位用kA, 可以认为是负的; E为正值, 单位为V·m-1; D单位为km。
2.2 以模式为基础的方法首先人们推导出了适用于各种闪电回击模式的有关远场和通道底部回击电流的表达式[23]。这些公式包括了一系列的参数, 尤其是回击速度v, 这个参数在很多例子中都是未知的。换句话说, 要想从相关的远距离电场或磁场中推导出闪电电流, 必须假设出回击速度的数值。然而当这个速度应用于不同回击时, 结果变化很大, 这个变化依赖于一定的远场和底部电流的关系, 所以当回击速度的估测出现一个误差就会导致在反演通道底部电流出现相当的误差[24-26]。实际上, 远距离电场和磁场峰值与回击电流峰值和回击速度是相关的。
2.3 随机方法Rachidi等[27]在采用传输线模式的基础上, 考虑了回击电流峰值I、回击速度v和远距离电场峰值E作为随机变量, 推导出如下公式:
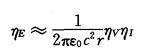
|
(2) |
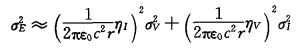
|
(3) |
公式(2)、(3)中忽略了电流峰值和回击速度的任何相关性[28]。其中, ηE, ηV和ηI, σE, σV和σI分别是峰值电场, 回击速度和峰值回击电流的方差。尽管对于单个事件, 在预先不知道回击速度的条件下, 从远场测量中获得足够准确的回击电流估测是不可能的, 然而从统计意义上来说这样是可行的。根据平均值和标准偏差, 利用闪电定位系统获得场的测量, 从独立测量为回击速度提供统计数据是可行的, 并且在闪电定位系统的覆盖区域内变化并不大。
3 结论和讨论闪电电流的可靠数据主要来源于利用设备塔或是人工引发闪电的直接测量以及由远距离电磁场的测量而反演估算得到。结果表明负地闪首次回击电流平均为30kA, 继后回击电流平均12kA。正地闪回击电流平均为35kA, 有时可达几百千安。高塔测量是主要的雷电流参量直接测量方法, 但不同高度测量的地闪回击电流无论峰值还是波形都存在一定的差异。人工引发雷电流的测量结果与自然闪电继后回击相一致。间接估测雷电流参数的方法随着地闪回击模式的发展将成为主要的方法。
从设备塔获得的闪电电流已经在不同的地区, 利用不同的测量设备测量得到。为了使用和对比这些数据, 我们必须理解不同被测量参数的明确定义, 测量系统的精确规范, 以及数据标准化的明确表述。另外, 在众多高塔中获得的闪电电流和电流衰减实验数据都清晰地显示了在塔顶和塔底的反射对测量电流的影响。因而, 如何评价在观测塔中所获得数据相对真实闪电电流的真实程度, 以及如何消除这种“污染”, 已经成为直接观测中需要解决的重要问题。
人工引雷作为目前研究闪电的一种重要手段, 虽然有它的不足之处, 如它的引发过程明显不同于自然闪电等, 但它仍然为测量和研究闪电物理过程、获取闪电各项参数及其参数之间的关系提供了一种比较有效的途径, 使时空随机发生的自然雷电变成在一定雷暴条件下可以控制地进行, 便于集中各种测量手段对雷电放电过程进行近距离综合观测, 为深入研究雷电物理、雷电探测、防护以及其它相关科学问题提供了一个有效的新途径。
对雷电流的间接估算是通过远距离观测到的电磁场来反演雷电流数据。这要求对雷电流和电磁场的关系有比较明确的认识。目前所采用的方法有三种, 分别是经验公式法、模式法和随机方法。但无论对雷电流参数的直接测量还是间接估算都还存在一定的科学问题, 资料的累积也还很不够, 仍需要更多的进一步观测和理论研究。
| [1] |
薛秋芳, 孟青, 葛润生. 北京地区闪电活动及其与强对流天气的关系[J]. 气象, 1999, 25(11): 15. |
| [2] |
Golde R.H.. Lightning[M]. London: Academic Press, 1977.
|
| [3] |
王道洪, 郄秀书, 郭昌明. 雷电与人工引雷[M]. 上海: 上海交通大学出版社, 2000.
|
| [4] |
Uman M A, Rakov V A, Rambo K J, et al. Triggered Lightning experiments at Camp Blanding[J]. Florida Trans IEE Japan, 1997, 117-B: 446-452. |
| [5] |
Berger K., Anderson R.B., Kroninger H. Parame ters of Lightning Flashes[J]. Electra, 1975, 41: 23-37. |
| [6] |
M. A. Uman. The lightning discharge[M], pp. 39. Florida, USA: Academic Press, Inc., 1987.
|
| [7] |
R. Cortina, E. Garbagnati, W. Serravalli, et al. Quelques aspects de l' évaluation des performances des réseaux électriques vis-à-vis de la foudre[G]. presented at CIGRE, Paris, 1980.
|
| [8] |
Fisher R.J., Schnetzer G.H., Thottappillil R., et al. Parameters of triggered-lightning flashes in Florida and Alabama[J]. Journal of Geophysical Research, 1993, 98: 22887-22902. DOI:10.1029/93JD02293 |
| [9] |
Rakov V.A. Transient response of a tall object to lightning[J]. IEEE Transactions on EMC, 2001, 43: 654-661. |
| [10] |
Janischewskyj W., Hussein A.M., Shostak V., et al. Statistics of lightning strikes to the Toronto Canadian National Tower (1978-1995)[J]. IEEE Trans.on Power Delivery, 1997(12): 1210-1221. |
| [11] |
W. Janischewskyj, V. Shostak, J. Barratt, et al. Collection and use of lightning return stroke parameters taking into account characteristics of the struck object[G]. presented at 23rd ICLP (International Conference on Lightning Protection), Florence, Italy, 1996.
|
| [12] |
V. Shostak. Modeling of return stroke current for lightning events at a complex tall structure[G]. presented at 2001 International workshop on electromagnetic radiation from lightning to tall structures, Toronto, Canada, 2001.
|
| [13] |
F. Heidler, J. Wiesinger, W. Zischank. Lightning Currents Measured at a Telecommunication Tower from 1992 to 1998[G]. presented at 14th International Zurich Symposium on Electromagnetic Compatibility, Zurich, Switzerland, 2001.
|
| [14] |
Depass. Statistics on artificially triggered lightning[J]. J.Geophys.Res., 1994a, 99(18): 515-522. |
| [15] |
Wang D, Rakov V A, Uman M A, et al. Characterization of the initial stage of negative rocket-triggered ightning[J]. J Geophys Res, 1999, 4213-4222. |
| [16] |
Fisher R J, Schnetzer G H, thottappillil R, et al. Parameters of triggered-lightning flashes in Florida and Alabama[J]. J Geophys Res, 1993. |
| [17] |
Anderson R.B., Eriksson A.J. Lightning parameters for engineering application[J]. Electra, 1980, 69: 65-102. |
| [18] |
Crawford D.E. Multiple-station measurements of tringgered lightning electric and magnetic fields[J]. M.S.thesis, Univ.Florida, Gainesville, 1980, 282. |
| [19] |
F. De la Rosa, K. Cummins, L. Dellera, et al. Characterization of lightning for applications in electric power systems[C]. in Task force 33. 01. 02-CIGRE, 2000: 35.
|
| [20] |
Guerrieri S., Nucci C.A., Rachidi F., et al. On the influence of elevated strike objects on directly measured and indirectly estimated lightning currents[J]. IEEE Transactions on Power Delivery, 1998, 13: 1543-1555. DOI:10.1109/61.714865 |
| [21] |
Rachidi F., Janischewskyj W., Hussein A.M., et al. Current and electromagnetic field associated with lightning return strokes to tall towers[J]. IEEE Trans.on EMC, 2001, 43. |
| [22] |
Rakov V.A., Thottappillil R., Uman M.A. On the empirical formula of Willett et al.relating lightning return-stroke peak current and peak electric field[J]. Journal of Geophysical Research, 1992, 97: 11527-11533. DOI:10.1029/92JD00720 |
| [23] |
Rachidi F., Thottappillil R. Determination of lightning currents from far electromagnetic fields[J]. Journal of Geophysical Research, 1993, 98: 18315-18320. DOI:10.1029/93JD01616 |
| [24] |
Idone V.P., Orville R.E. Lightning return stroke velocities in the Thunderstorm Research International Program (TRIP)[J]. Journal of Geophysical Research, 1982, 87: 4903-4915. DOI:10.1029/JC087iC07p04903 |
| [25] |
Mach D.M., Rust W.D. Photoelectric Returnstroke velocity and peak current estimates in natural and triggered lightning[J]. J.Geophys.Res., 1989, 94(13): 237-13, 247. |
| [26] |
Rakov V.A., Dulzon A.A. Results of calculation of the electromagnetic fields of lightning discharges[J]. Tekhnicheskaya Elektrodinamika, 1987, pp:87-89. |
| [27] |
Rachidi F., Bermudez J.L., Rubinstein M., et al. On the estimation of lightning peak currents from measured fields using lightning location systems[J]. Journal of Electrostatics, 2004, 60: 121-129. DOI:10.1016/j.elstat.2004.01.010 |
| [28] |
Rakov V.A., Uman M.A.. Lightning:Physics and Effects[M]. Cambridge University Press, 2003.
|
 2006, Vol. 32
2006, Vol. 32