在数值分析中, 绘制等值线是应用最多的基础技术手段之一, 在地质、气象、水文、设计等领域中得到了广泛应用。绘制等值线是对大量离散的又具有一定规律的几何量值或物理量值, 用数学的方法插值变换成图形的过程。各种网格法绘制等值线的步骤一般为:离散数据网格化, 网格点数值化, 等值点追踪, 光滑和绘制等值线[1]。绘制等值线常用的方法有网格法和三角网法。三角网法是针对离散数值点构建三角网进行内差追踪, 绘制方法比较复杂且是纯数学方案, 忽略了离散点网格化在气象资料中的噪音过滤和尺度分离等, 直接采用中国气象局下发的球面网格资料可以避免此问题。网格的等值点追踪算法有以下几种:随机追踪法、最近点连接法、按固定方位次序追踪法。通常这些算法比较复杂而且难懂[2]。很多气象自开发软件中, 较常用的方法是应用外部软件, 如结合g rads, surfur等外部软件来实现。一般的思路是:先按照软件要求写出特定数据格式; 然后选择内差法, 用地理信息系统(GIS)绘制底图, 限定边界, 填充设置等, 然后调用软件模块生成图形; 最后显示生成的图形[3]。这增加了不少中间环节, 且对等值线的绘制原理仍然不清楚, 且在响应速度上尤其是频繁调用时也对计算机要求更高。本文解析了等值线绘制的具体方法:用按顺序追踪和区域极值点相结合, 采用三象限扫描法"追踪各点, 思路清晰明了, 算法简便, 容易实现。实际结果与手绘图一致, 线条流畅、响应很快, 效果不错。
1 绘图前准备首先要建立球面网格与绘图平面直角坐标的对应关系, 设置相应的放大缩小比例参数、地图投影选择参数等。
2 不规则点绘制平滑曲线[4]在VC++的绘图函数中, 引入各不规则点利用PolyBezier函数就可以绘制出平滑曲线。在计算机图形学中, 通常采用Bezier函数或B样条函数来拟合曲线。拟合曲线通常只关心曲线走向, 不关心曲线是否经过各控制顶点(各不规则点连接成的多边形顶点)。而对于气象等值线不经过各等值点误差太大, 甚至是错误的, 需要矫正。Bezier函数或B样条函数都是在起点到终点之间构造差值多项式混合函数来进行逼近拟合, 通常由n+1个控制顶点定义一个n次多项式。比较而言, B样条曲线可采用分段Bezier曲线的表示, 且具有更大的灵活性, 同时考虑低次曲线计算量小, 又要符合曲线要求, 实例采用四阶三次B样条曲线。
三次B样条曲线造型比较灵活, 有以下属性:构造直线段, 只需要四顶点共线; 构造尖点需要构造两重、三重顶点或节点。为使曲线与直线相切, 只要取三顺次点位于直线上, 则曲线在第二点与直线相切。
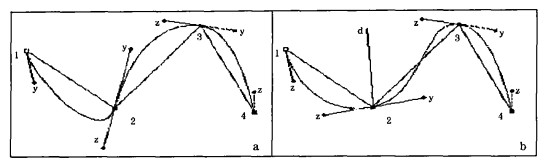
利用样条曲线与直线相切的特性, 不规则点中每点增加左右两控制顶点构造三点共线。三点共线的情形很多, 要选择最适合曲线的方式。对于图 1a中, 2点左边下凹, 有损美观, 也违背了绘图原则, 人为地制造了局部的高值或低值极点。图 1b中, 2d为∠123的角平分线, 图形显得更合理。于是, 此处约定, 增加的控制顶点位于该点与前后相邻点组成角度的角平分线的垂线上, 即2点的控制顶点在角平分线2d的切线上。从图中还可以发现, 某点的切线段越长, 曲线靠近切线的弯曲程度越大, 反之越小。实际上, 要使曲线有较合理走向, 则增加点切线段的长度与原顶点线段在切线上的投影长度相关, 如图 1b中2z的长度与线段12在2z上的切线投影相关。所以, 根据实际绘制效果, 程序采用下面公式决定切线段长度(r):基本伸展长度(TR), 投影长度(temp), 缩放系数(α), L为原顶点间的距离:
|
图 1 增加构造控制顶点的不同方法 a.第2点任意构造b.第2点由角平分线和距离决定 |
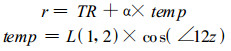
|
其中TR取0.0, α取0.4286(3/7)。
对于闭合曲线, 分为周期闭合和非周期闭合。程序采用周期闭合的方法处理, 曲线更光顺, 方法与上面类似。增加控制顶点后, 利用VC函数就可以直接画线了。
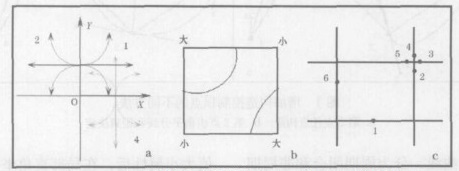
3 规则四方矩阵网格点的追踪 3.1 三象限扫描法在等值线图中, 沿着等值线切线方向, 左右两边的大小属性是一直不变的, 即左边一直是或高或低于右边。只要找到起点, 确定此大小属性后, 用"三象限扫描法"就可以追踪各点。"三象限扫描法"是指在局部直角坐标中, 对于规则四方矩阵网格, 任意与网格线相交的点依照大小属性的设定, 在1、2、4象限每个象限沿着3个方向(如图 2a所示), 通过网格点之间的数值内差和空间位置内差, 采用递归调用就能查找出与这一点等值且位置依次临近的点, 在回到起点或到达边界时停止追踪, 从而得到等值点组的方法。
|
图 2 三象限扫描法和等值点追踪可能出现的特殊情形 a.三象限扫描法b.双等值线经过同一网格c.等值线近距离按顺序绕过网格点 |
网格中, 任意的经纬度(×10处理)除以格距(等值线间距)忽略掉余数后必然对应一个网格点O, 即局部直角坐标零点(包括网格点本身)。网格线上任一点确定数值大小属性后, 在局部直角坐标系中用三象限扫描法, 按照固定的数值属性, 就可以遍历全网格, 追踪出等值点。起点方向选择时, X网格线上的点从上下方向、Y网格线上从左右方向开始追踪。
3.2 特殊情形还有两种情形需要特别处理:一是网格对角线上的点同为大和同为小的情形, 这时同一网格内可能有两条相同数值等值线经过, 如图 2b所示。二是对于等值线正好在网格点上的追踪。第一种情形采用全网格筛选, 将对角线上数值同为大或和同为小的情形进行标注, 计算出该区域可能出现的歧点。追踪时对经过该区的数值点进行使用标记, 使用过的点就不再使用, 没有使用过的点采用距离近的点优先使用, 保证临近系统的等值线不出现交叉。
第二种, 等值线经过网格点时会出现无法追踪情形的处理。网格资料预处理:在追踪之前, 进行全网格资料搜索, 对正好在等值线上的网格点的数值±ε(ε为一正的小量, 这里取0.1), 在数值内差时就不会出现经过格点无法追踪的情形, 但可能得到多个(不超过4个)临近数值点(如图 2c), 需要过滤处理。特别说明的是, 等值线格距较大时, 对于局部极值网格点(指上下左右包括自身共5点中的极值), 在绘制等值线时, 数值±ε很可能漏掉小尺度(曲率小)天气系统。如此改进:局部极大值网格点数值+ε, 极小值-ε, 其他情形随意处理对系统形势影响很小。有多个临近点曲线绘制效果不好, 可以将多点合一, 或是取一个而忽略其他临近点, 对结果影响不大。另外, 在四个角上也存在两点画曲线的可能, 增加第三点0.8 ×(X1+X2), 0.8 ×(Y1+Y2)就可以画线了(X1, Y1, X2, Y2分别是首尾两点的坐标)。
3.3 遍历性说明在等值线图中, 只有两种形式:一是闭合; 二是中止于边界的线。先计算出在边界需要划线的所有起点, 沿起点开始追踪, 结束点在边界点数组里查找进行使用后标记, 避免在第二次追踪时重复计算, 绘制出所有非闭合等值线。在全网格查找高值或低值中心(非边界9点, 边界6点或4点), 然后在非边界中心附近进行逐步外推内差, 出现中止于边界的数值点时就停止外推。即通过中心只搜索闭合曲线, 通过边界只搜索非闭合曲线, 从而达到追踪全部等值点的目的。
4 程序的其他说明图 3是该程序的绘图结果。对于CPU是Intel Celeron 900M H z, 内存256M, 主板自带显卡, 操作系统Window s 2000 Professio nal, 程序绘制6张形势图, 需要0.08秒左右, 线条, 图像放大、缩小、滚动显示更新都很流畅, 对比手绘的格点资料图, 效果很相近。

|
图 3 绘图结果示意 |
| [1] |
黄淼云, 张学忠, 辛冬根, 等. 计算机图形技术[M]. 北京: 人民交通出版社, 1995.
|
| [2] |
陈润米. 计算器绘图[M]. 北京: 清华大学出版社, 1998: 129-136.
|
| [3] |
章毅之, 辜晓青. 气象要素的等值线绘制技术[J]. 江西气象科技, 2002, 2: 30. |
| [4] |
新世纪网络课程建设工程. 几何造型技术[J/OL]. http://www.lnnu.edu.cn/xdjyjx/tuxing.
|
 2006, Vol. 32
2006, Vol. 32