2. 江西省人工影响天气办公室
2. Jiangxi Province Weather Modification Office
在众多大气因子中, 风场资料是分析天气演变最直观和最有价值的资料之一[1]。根据风场的演变, 可以了解中小尺度等强对流天气发生发展的某些重要物理过程[2]。比如:高空槽脊的空间位置; 高、低空急流的强度、深度; 冷暖平流的分布及其与强风暴直接相关的垂直风切变的演变等。新一代天气雷达6分钟一次体扫资料, 可连续获取不同高度风向、风速数据, 并以风廓线产品形式表现出来。雷达探测信号足够强的话, 最大探测高度可达15.2km。但是, 雷达风廓线产品也存在某些局限性[3]。比如:少于25个数据点时, 没有风数据显示; 均方根误差超过某一数值时, 也没有风数据显示等。尤其是当测站上空有中小尺度系统扰动或低值系统过境时, 风廓线产品的误差会明显加大或完全不可用。此外, 高仰角时风数据也明显存在误差。为了解产生误差与不确定因素的某些原因, 发挥新一代雷达风廓线产品在短时天气预报和强对流天气临近预警预报中的作用, 利用南昌新一代天气雷达获取的2002-2005年4-6月37次(共计614组样本)完整风廓线与南昌同期探空风资料进行了相关分析, 所得到的部分计算结果, 对提高短时临近预报的准确程度起到一定作用。
1 资料处理首先, 对南昌雷达站2002-2005年4-6月37次(共计614组样本)完整风廓线资料, 按照每隔300m读取雷达风廓线实况资料, 直到数据读完止; 然后, 读取相同时间、相同高度的探空风资料; 最后, 利用数理统计分析方法, 对上述配对(相同时间相同高度的雷达风廓线与探空风资料)的风向风速资料分别进行相关分析。计算结果见表 1。
|
|
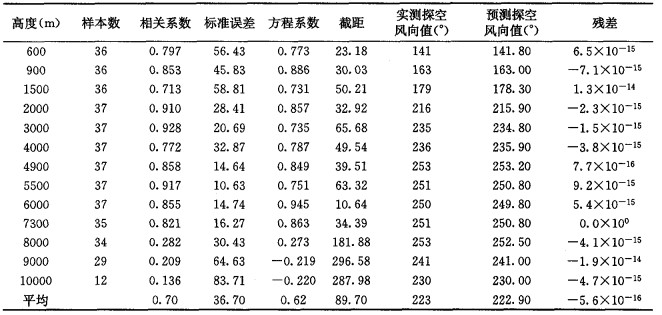
表 1 2002—2005年4—6月不同时间探空与雷达风廓线风向风速相关计算结果 |
表 1是2002-2005年4-6月不同时间探空与雷达风廓线风向风速相关计算(均值)结果。由表 1可知, 风向相关系数平均为0.74;相关系数R≥0.6次数29次, 占总数78%;R≥0.8次数22次, 占总数60%;相关系数R < 0.6次数8次, 占总数22%;标准误差为26.87;残差为4.4×10-15; 实测探空风向215.3°; 预测探空风向220.8°; 方程系数和截距各为0.74、66.45。
2.1.2 风速相关分析结果由表 1可知, 风速相关系数平均为0.75。相关系数R≥0.6次数30次, 占总数81%;R≥0.8次数7次, 占总数57%;相关系数R < 0.6次数7次, 占总数19%。标准误差为3.13;残差9.4×10-17; 实测探空风速为12.26(m.s-1); 预测探空风速为12.68(m.s-1)。
2.1.3 回归方程的建立计算得到探空风廓线与雷达风廓线的风向、风速回归方程:
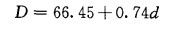
|
(1) |
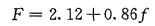
|
(2) |
式中D和d分别为探空和雷达风向, F和f分别为探空和雷达风速。
由风向、风速回归计算结果可知, 新一代雷达测风(风廓线)与探空测风有较强的相关关系; 平均标准误差相对变量均较小; 预测值与实测值之间的平均残差均较小; 这说明回归方程可靠性比较大。
2.2 不同高度的探空风向与雷达风向相关分析结果分别对600、900、1500、2000、3000、4000、4900、5500、6000、7300、8000、9000、10000m等13个高度的探空风与雷达风的风向资料相关计算, 结果见表 2。由表 2可知, 600~10000m相关系数R平均值为0.7。其中600~7300m相关系数R平均值为0.84;标准误差平均值29.9;方程系数平均值0.82;截距平均值39.9;实测探空风向平均值217.5°; 预测探空风向平均值217.4°; 残差平均值2.02×10-15。8000~10000m相关系数R平均值为0.2;标准误差平均值59.6;方程系数平均值-0.06;截距平均值255.5;实测探空风向平均值241.3°; 预测探空风向平均值241.2°; 残差平均值-9.1×10-15。
|
|
表 2 2002—2005年4—6月不同高度探空风向与雷达风向相关分析数据 |
计算结果还表明, 600~7300m雷达风廓线与探空风廓线相关性很好, 标准误差较小, 残差也较小。8000~10000m雷达风廓线相关性急剧降低, 与前者比, 标准误差急剧加大, 方程系数也呈现负值, 这表明两者之间呈现负相关。
3 实例检验为了验证2002—2005年4—6月获取的雷达风廓线资料与同期探空风廓线相关分析结果的可靠性, 任取2005年8月13日19:00探空风资料, 进行了实例检验与验证。从8月13日19:00探空与雷达风向风速数据中共读取到各27组样本; 其中:探空风向平均值111.70°, 雷达风向平均值109.10°; 探空风速平均值16.60m·s-1, 雷达风速平均值19.50m·s-1。将两组雷达风数据分别代入回归方程式(1)、(2)进行计算验证, 得到两组新数据结果:

|
(3) |
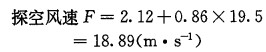
|
(4) |
与实测值比较, 探空风向计算值与实测值相差35.48°, 相对误差31.78%;探空风速计算值与实测值相差2.29m·s-1, 相对误差13.86%。
4 误差原因分析虽说雷达测风与探空测风之间存在良好的相关性。但是, 由于雷达风廓线产品存在一定的局限性, 比如:当中小尺度系统扰动及高空槽、脊过境时, 往往会导致雷达测风风场起伏及随高度增加风数据失真等, 造成雷达测风数据资料出现误差。下面列举2个实例, 说明在不同天气背景条件下, 探空测风与雷达测风的风数据间的差异。
(1) 强风暴天气背景条件下探空测风与雷达测风数据间的差异
2003年4月12日, 江西境内出现了以冰雹、强风暴、短时强降水为主的强风暴天气。受其影响, 赣东北弋阳出现了强风暴天气, 县城降雹最大直径达50mm, 损失较为严重。根据4月12日07:00探空与雷达观测风数据计算结果为:风向相关系数0.029, 风速相关系数0.7481;两者相关不是很好。从07:23—08:31雷达风廓线图形变化(图略)可知, 南昌测站上空冷暖气流交绥频繁, 中小尺度系统持续扰动, 冷空气扩散引起的动量下传等, 造成大范围“ND”无数据区, 正是此次探空测风与雷达测风数据间相关不好的主要原因。
图 1是2003年4月12日07:00探空与雷达风廓线变化。由图 1a看出, 探空风向在低层, 风向出现了一个从90至260°的跃增, 随后一直在250°~270°间维持, 显示了强风暴前夕暖湿气流的积累过程。雷达风向在低层, 却显示出了与探空风向截然不同的走向, 风向从0.5km的210°转到70°, 1.5km开始雷达风廓线走向才与探空风走向趋于一致。由于低层探空与雷达间风向的背道而驰, 才造成强风暴背景条件下探空测风与雷达测风数据间的差异。由图 1b看出, 探空风速从0.5~7.0km随高度逐渐加强, 这表明了垂直风速切变加强; 雷达风速从1.5km才开始呈现随高度增加的趋势。由于冷空气影响, 雷达低层风速与探空风速基本反向, 而且风速波动明显。

|
图 1 2003年4月12日07:00探空与雷达风廓线变化(a风向, b风速) 实线:探空, 虚线:雷达 |
(2)强对流天气背景条件下探空测风与雷达测风数据间的差异
2004年4月23日出现了一次以雷雨大风为主的大范围强对流天气。雷达风廓线产品显示, 从300m到12km出现了连续风场(图略), 高、低、中层配合极好, 呈现有利于强对流天气发生发展的暖平流分布。20:00地面图上冷空气主体尚在新疆, 江西处于入海高压后部, 中低层处低压环流中, 高空处槽前西南气流中; 天气背景有利于强对流的发生发展。根据4月23日19:00探空与雷达观测风数据计算结果表明, 雷达风廓线分布与探空风廓线分布吻合。风向相关系数0.9936, 风速相关系数0.9488;两者相关很好。图 2是2004年4月23日19:00探空与雷达风廓线变化。由图 2看出, 探空与雷达测风的风向、风速变化几乎完全吻合, 趋势完全一致。类似风向、风速变化趋势完全一致的个例并不多, 但单独的风向或风速分布中有90%吻合的个例, 却不在少数, 约占总数40%以上。
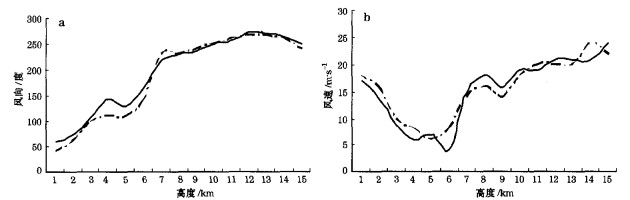
|
图 2 2004年4月23日19:00探空与雷达风廓线变化(a风向, b风速) 实线:探空, 虚线:雷达 |
通过对2002—2005年4—6月雷达风廓线资料与同期探空资料相关分析, 并对结果进行验证和误差分析, 结果表明:
(1) 风向相关系数平均值为0.74。其中:相关系数R≥0.6次数29次, 占总数78%;R≥0.8次数22次, 占总数60%;R < 0.6次数8次, 占总数22%。风速相关系数平均值为0.75。其中:相关系数R≥0.6次数30次, 占总数81%;R≥0.8次数7次, 占总数57%;R < 0.6次数7次, 占总数19%。风向、风速相关系数值随高度增加减少, 其中600~7300m相关系数平均值R=0.84;8000~10000m相关系数平均值R≈0.2。
(2) 与实测值比较, 探空风向计算值与实测值相差35.48°, 相对误差31.78%;探空风速计算值与实测值相差2.29m·s-1, 相对误差13.86%。中小尺度系统扰动和冷空气动量下沉造成数据的凌乱及随高度增加雷达风数据减少等, 是造成误差主要原因。
(3) 雷达风廓线产品, 可以很好预示降水持续时间和天气激烈程度。但是, 要使其在强风暴、强对流天气短时预报中发挥作用, 需反复对探空测风与雷达测风数据资料进行比较, 寻找不同天气系统间风廓线变化规律, 使其与探空风数据资料误差降到最小。
| [1] |
王改利, 刘黎平. 多普勒雷达资料在暴雨临近预报中的应用[J]. 气象, 2005, 31(10): 12-15. DOI:10.7519/j.issn.1000-0526.2005.10.003 |
| [2] |
张培昌, 杜秉玉, 戴铁丕. 雷达气象学[M]. 北京: 气象出版社, 2001.
|
| [3] |
彭治班, 刘健文, 郭虎, 等. 国外强对流天气的应用研究[M]. 北京: 气象出版社, 2001.
|
 2006, Vol. 32
2006, Vol. 32