2. 安徽四创电子股份有限公司,合肥 230088
2. Anhui Sun-Create Electronics Limited Company
冰雹识别一直是气象界的一大课题, 在混合相态降水中区分出冰雹信号对于人工影响天气的作业指挥和效果评估以及强天气预警和水文模式的参数初始化都有十分重要的意义。天气雷达观测和研究表明, 利用单一的回波强度信息从混合云中区别不同的降水粒子相态是困难的。常规天气雷达和多普勒雷达只能测量到与降水强度相关的一个参量———反射率因子, 单纯用它来识别冰雹的能力非常有限。另一方面卫星遥感云和降水粒子的相态也主要局限在云的顶部, 而且很难区分出混合区中冰雹粒子。具有双线偏振功能的多普勒雷达系统可以探测到水平偏振反射率因子ZH、差分反射率因子ZDR、差传播相移KDP、水平偏振和垂直偏振回波功率零滞后互相关系数ρHV等与降水粒子类型、形状和分布以及下落运动等要素密切相关的参数, 从而可以得到降水粒子微物理结构的额外信息, 因此使得探测混合区降水粒子的冰雹成为可能。但如何估测冰雹粒子是双线偏振雷达应用研究中的一个迫切需要研究和解决的问题。自1980年代以来, 国外学者的工作主要可以分为两种类型[1]:(1)对降水粒子的形状、密度、谱分布作假设, 分别作散射计算, 得到它们的雷达参量的特性, 然后结合雷达观测的资料来进行冰雹的识别。(2)结合水凝物在云中的发展演变模式或云模式的结果进行散射计算, 分析云中粒子的时空分布变化。我国自20世纪80年代中期以来, 也进行了多波长雷达、偏振雷达探测冰雹云的研究。刘黎平等[2, 3]建立了C波段双线偏振雷达识别冰雹区的方法。钱永甫等人[4]在此基础上, 分析了两次降水过程中云内粒子的相态及大小的空间分布得出:负值ZDR对应于大冰雹, 正值ZDR对应于小雹融化所形成的大雨区。漆梁波等人[5]利用三维冰雹云模式, 详细讨论了云雨衰减作用和云中各粒子共存于同一空间给双线偏振雷达识别冰雹带来的影响。总的来说, 国内外学者在这一领域取得了很多成果, 但是这种研究大多处于半经验半理论阶段, 未能达到业务可用的水平, 特别是对冰雹云中粒子的识别和定量化。
随着我国新一代多普勒雷达系统组网工作基本结束并逐步投入业务运行, 许多国内雷达生产厂家都致力于在多普勒天气雷达系统的基础上升级双线偏振功能的研究, 双线偏振多普勒雷达探测理论和方法及其在气象、水文、航空领域的应用越来越有现实意义, 但是由于各种原因, 目前在国内尚未真正完成具有双线偏振功能的多普勒雷达的改造。本文立足于中国气象局即将研制的双线偏振多普勒天气雷达系统, 借用美国KOUN雷达的观测资料, 进行了利用双线偏振雷达资料识别冰雹信号的方法分析, 并对其在实际运用中的合理性和可行性进行分析探讨, 为我国的双线偏振雷达业务运行提供参考。
1 冰雹粒子的偏振参数特性对冰雹的发生和形成雹块大小的预测是雷达气象学家们关注的一个重要问题, 冰雹粒子的一些物理特性有助于利用偏振雷达的参数将其从其它降水粒子中区分开来, 然而由于冰雹粒子在下降过程中的空间取向还没有彻底的研究清楚, 因此要准确测量出其尺寸大小还是很困难的。List[6]等人研究了冰雹粒子尺寸和形状之间的关系, 认为:直径在5~10mm之间的冰雹粒子一般呈球形或圆锥形, 直径在10~20mm之间的冰雹粒子一般呈椭球形或圆锥形, 直径在10~50mm之间的冰雹粒子呈椭球形, 但是在短轴上会有一些凸起, 直径在40~100mm之间的冰雹粒子呈球形外围多有一些突起。而且冰雹粒子越大, 其形状越不规则, 冰雹粒子的大小和那些外围突起之间没有简单的关系。另一研究表明, 大多数冰雹粒子都有一定的偏心率, 如83%的冰雹粒子其偏心率在0.6和1之间, 15%的冰雹粒子其偏心率在0.4和0.6之间, 而不到2%的冰雹粒子偏心率小于0.4, 绝大部分的地面降雹雹块其偏心率在0.8左右。一般湿冰雹的偏心率在0.8左右, 而软雹的偏心率在0.6~0.8之间。冰雹下落过程中的空间取向是一个比较困难的问题, 直径在10~50mm之间的椭圆形冰雹粒子下落过程中比较稳定, 长轴保持在垂直方向上, 而尺寸较小的冰雹粒子一般认为在下降过程中由于其空中翻滚而呈球形或各向同性的特点[7]。
目前, 大多数双线偏振多普勒雷达能得到的雷达偏振参数包括雷达水平反射率因子(ZH)、差分反射率因子(ZDR)(两种极化下反射率分贝差)、差分传播相移(KDP)(差分是指相移差对距离的微分)、零滞后互相关系数(ρHV)等, 其中ZH为目标对水平极化电磁波的回波反射率因子(反射率因子是与雷达常数无关的目标散射特征量), 它与降水粒子的数目和尺寸大小有关; ZDR为差分反射率因子, 它与粒子形状关系密切, 主要表征降水粒子的空间取向和长短轴之比; KDP是差分传播相移, 表征不同偏振分量在传播路径上, 因传播系数不同引起的相位的变化; ρHV反映了水平偏振和垂直偏振回波功率之间的相关系数。由于冰雹粒子的形状和空间取向是一个复杂的问题, 且在其下落过程中的运动方式比较复杂, 常伴有翻转运动。因此, 冰雹粒子产生的ZDR随其形状、大小、空间取向以及下落运动等不同会产生较大的差异。一般来说, 虽然冰雹呈现为一个主轴在垂直方向上的椭球形状, 但是由于其在下落过程中不断翻转、摆动, 因此其ZDR值趋于0。除非是尺寸较大的大冰雹, 由于其在下落过程中保持自由降落状态, 从而导致其ZDR值小于0, 而冰雹的外覆水膜可以极大地改变其ZDR的值。在混合相态的降水粒子中, KDP主要是由液态降水产生的, 固态降水粒子产生的KDP一般较小, 而ZDR的产生却是两者共同作用的结果, 这点在识别降水粒子相态中至关重要。至于ρHV, 一般来说, 冰雹产生的ρHV信号要小于液态水的ρHV值, 在冰水混合区, 其ρHV一般都比较小[8]。
2 利用双线偏振雷达测量参数识别冰雹的几种方法 2.1 水平反射率因子ZH法Mason提出ZH超过55dBz可以作为冰雹出现的指标。事实上, 当在0℃层以上出现的ZH大于45dBz时就可以认为出现冰雹。根据这一结果, 可以采用参量YZ来识别冰雹区:
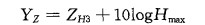
|
(1) |
其中ZH3定义为0℃层以上3km以上最大回波强度(dBz), Hmax为最大回波强度所在高度(km)。YZ>60时就认为有冰雹区存在。
2.2 指标系数HDR法K.Aydin和T.A.Seliga[8]等人发现纯液态水的ZDR值通常是大于0, 变化范围在0~4dB之间, 与水平反射率因子ZH成正相关。而与周围雨区较大的ZDR相比, 冰雹的ZDR值一般在0dB左右, 同时ZH为一个高值区。根据这一结果, 他们提出用参量HDR=ZH(dBz)-f(ZDR)来判断冰雹区, 当HDR>0时, 就认为有冰雹区存在, 其中f(ZDR)取值见下式[7]:
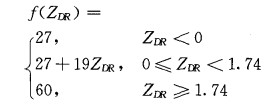
|
(2) |
几个原因使得KDP对冰相粒子不敏感:首先, 冰相粒子的介电常数要小于液态水, 对于大尺寸的湿冰雹(D>20mm)来说, 粒子的外覆水膜很薄, 仅仅是边缘部分的介电常数增大。其次, 冰雹的密度要低于其它的降水粒子。最后, 冰雹在下落过程中呈现的翻转使得其表现了粒子的各向同性的性质, 因此, 对于纯冰雹来说, 其KDP值近似为0。根据上述分析, 定义系数Kdr:
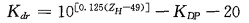
|
(3) |
当Kdr>1(°)·km-1时, 就认为有冰雹区存在[7]。
2.4 模糊逻辑识别法为了取得更好的效果, 在综合分析上述方法的基础上, 建立了利用模糊逻辑法来识别冰雹的识别模式(关于该方法请详见参考文献[9])。模式中输入变量为ZH、ZDR、KDP和ρHV, 输出结果为干冰雹(DH)、小的湿冰雹(SWH)、大的湿冰雹(LWH)、巨型湿冰雹(GWH)以及冰水混合物(H+R)五类冰雹粒子。
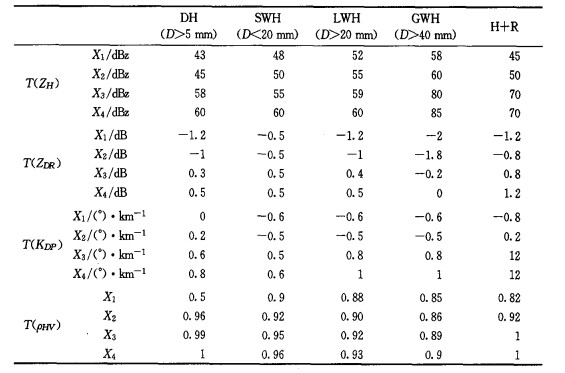
利用模糊逻辑法识别冰雹粒子的相态, 首先要构造隶属函数, 然后利用隶属函数来对雷达测量参数进行模糊化。模糊化以后, 进行IF-THEN规则推断, 然后采用集成的方法进行集成。最后一步是退模糊, 即将集成的结果转化成单一的降水粒子类型[9-13]。表 1给出了用于构建隶属函数的基本参数值。在构建隶属函数时, 选用不对称的T函数作为隶属函数基本的基本形式, 该函数形状由4个参数决定:左起始点值X1, 左区间点值X2, 右区间点值X3, 右结束点值X4, 是一个关于区间[X2, X3]取值的函数[式(4)][11]。
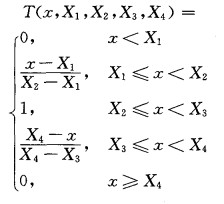
|
(4) |
|
|
表 1 4类冰雹的隶属函数参数设置 |
美国S波段KOUN雷达是在WSR-88D雷达的基础上增加双偏振功能后升级而来的, 它采用的是同时收/发水平和垂直偏振波的方案。本节讨论所用的数据就是由KOUN雷达于2003年5月10日在Oklahoma州的JPOLE试验中采集的。根据当时的天气实况资料, 这次过程自KOUN雷达测站的东南方向向东偏北方向移动。在位于KOUN雷达的东部地区有很强的龙卷对流单体出现, 在19:03UTC左右, 这些对流单体产生了很强的冰雹信号。图 1(见彩页)给出了19:03UTC左右的PPI图, 四张图依次是ZH(左上)、ZDR(右上)、KDP(左下)、ρHV(右下), 雷达观测仰角是0.5°, 最大观测距离300km, 每个距离圈的间隔长度60km, 径向射线之间的间隔为30°, 雷达位置位于半圆的圆心处, 所有资料已经经过预处理。由图 1中ZH的回波图上可以明显看到一个强回波中心A区(中心位于方位93°、距离130km处), 中心最大强度达到70dBz以上。而在其它三张对应的图上相应的位置, 在最强ZH的中心位置都有ZDR < 1dB和KDP>(1°)·km-1区, 同时对应的ρHV出现一个相对明显低于周围的低值区, 这些符合冰雹出现的特征, 表明该处已经出现冰雹, 并且冰雹可能已经降落地面(该区的位置离地面的高度大约1km)。美国NSSL提供的地面资料也表明该地区此时确实出现了较大的冰雹。
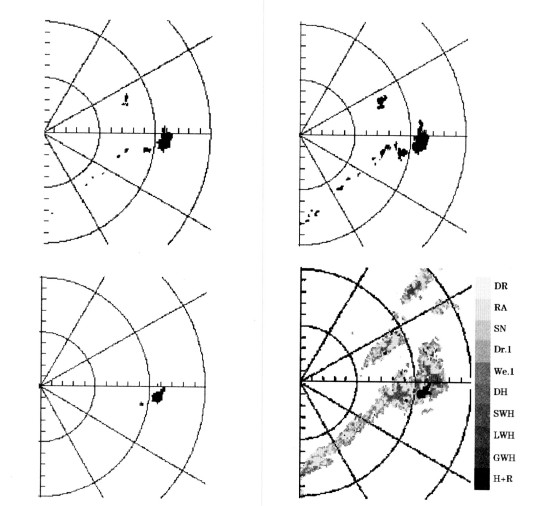
图 2是利用上述几种方法识别得到的冰雹区图像, 从图 2的结果可以看出, 上述几种方法都可以识别出相关的冰雹出现的区域, 识别出的冰雹区都表现出较明显的冰雹偏振参数特征:在冰雹区中心, 反射率大于65dBz, 而ZDR在0.05dB左右, 高的反射率ZH和低差分反射率ZDR值表示有翻滚的冰雹。而在冰雹区的边缘向外, 反射率逐渐减小(由50dBz以上逐渐减小到40dBz左右), ZDR逐渐变大(由1dB逐渐增加到3dB左右), 高的ZH和高的ZDR表示大雨或大的液态水滴, 反映了冰雹区周围仍然是强的降水区[14, 15]。识别的结果同理论分析的结果基本一致, 表明用这几种方法都可以用于冰雹识别。
|
图 2 分别利用水平反射率因子ZH法(a)、指标系数HDR法(b)、差分传播相移系数Kdr法(c)和模糊逻辑识别法(d)识别得到的冰雹区 雷达位于半圆的中心位置, 图a、b、c中黑色区域为冰雹区 |
当然, 这几种方法得到的结果之间的差异还是比较比较明显的(图 2):一个最明显的特点就是利用模糊逻辑法在进行冰雹识别时, 不仅可以识别出具体的冰雹位置, 而且还可以对冰雹进行分类(干冰雹、小的湿冰雹、大的湿冰雹、巨型湿冰雹以及冰水混合物五类)。这是由于利用模糊逻辑法分类比较细的缘故。事实上, 如果能够具体再分析一些冰雹粒子的结构特征, 还可以进行进一步的细分, 这就是用模糊逻辑法的最大特点和优点。其它的三种方法虽然得到的结果跟我们选用的参数阀值有一定的关系, 但是不管设定何种值, 其最终结果只能给出是或不是冰雹粒子, 不能对冰雹粒子的类型作进一步的分类。
另外, 从图 2d还可以看出, 在冰雹区的边缘地区的冰水混合区, ρHV降低到0.9以下, 甚至在一些共振散射区, ρHV值会下落到0.5以下。认为这是由于冰雹粒子的外覆水膜以及冰相粒子和液态粒子不同尺寸、不同轴比混合在一起以及冰雹在下落过程中的翻滚, 使得返回的水平和垂直偏振信号的相关性较差的原因[16]。
4 结语(1) 基于模糊逻辑法利用双线偏振雷达观测资料建立的识别模式, 可以比较有效地识别混合降水区中冰雹的位置, 其识别的结果比较符合实际的天气过程, 但是还需要更多资料来做进一步的研究和验证。该方法比较简单, 在实际的业务运行中, 可以根据给出的冰雹位置指导人工影响天气作业。
(2) 利用本文构建的模式, 不仅可以识别出冰雹的具体位置, 而且还可以对降雹粒子进行分类, 因为不同类型的冰雹其偏振特性有比较明显的差别。
(3) 对识别冰雹区的结果分析可以发现, 在冰雹区的边缘地区的冰水混合区中, ρHV相关性较差, ρHV值在0.9以下, 甚至在一些共振散射区, ρHV值会下落到0.5以下。
致谢:作者感谢美国NSSL的张竼菲博士提供了KOUN雷达资料。
| [1] |
Tuttle J.D. Multiparameter radar study of a microburst:comparison with model results[J]. J. Atmos. Sci, 1989, 46: 601-620. DOI:10.1175/1520-0469(1989)046<0601:MRSOAM>2.0.CO;2 |
| [2] |
刘黎平. 双线偏振多普勒天气雷达估测混合区降雨和降雹方法和理论研究[J]. 大气科学, 2002, 26(6): 761-772. |
| [3] |
刘黎平, 王致君, 徐宝祥, 等. 我国双线偏振雷达探测理论及应用研究[J]. 高原气象, 1997, 16(1): 99-105. |
| [4] |
钱永甫, 刘黎平. 用双线偏振雷达研究云内粒子相态及尺度的空间分布[J]. 气象学报, 1996, 54(5): 590-598. DOI:10.11676/qxxb1996.061 |
| [5] |
漆梁波, 肖辉, 黄美元, 等. 双线偏振雷达识别冰雹的数值研究[J]. 大气科学, 2002, 26(2): 230-240. |
| [6] |
List R, Schemenauer R. Free-fall behavior of planar snow crystals, conical graupel, and small hail[J]. J. Atmos. Sci, 28: 110-115. DOI:10.1175/1520-0469(1971)028<0110:FFBOPS>2.0.CO;2 |
| [7] |
Straka J M, Zrnic D S, Ryzhkov A V. Bulk hydrometeor classification and quantification using polarimetric radar data:synthesis of relation[J]. J. App. Meteo, 2000, 39: 1341-1367. DOI:10.1175/1520-0450(2000)039<1341:BHCAQU>2.0.CO;2 |
| [8] |
Aydin K., T.A. Seliga, V. Balaji. Remote sensing of Hail with a Dual Linear polarization radar[J]. J. App. Meteo, 1986, 25: 1475-1484. |
| [9] |
Hongpinlu, V. Chandrasehar. Chandrasehar, Classification of Hydrometeros Based on Polarimetric Radar Measurement:Development of Fuzzy Logic and Neuro-Fuzzy System, and In Situ Verification[J]. J. Atmos. and Oceanic Tech., 2000, 2: 140-159. |
| [10] |
Lawrence D, Carey, Steven A. Rutledge, Correcting Propagation Effects in C-Band Polarimetric Radar Observations of Tropical Convection Using Differential Propagation Phase[J]. J. App Metero., 2000, 9: 1405-1432. |
| [11] |
N.Balakrishnan, D.S.Zrnic. Estimation of Rain and Hail in Mixed-Phase Precipitation[J]. .J. Atmos. Sci, 1990, 3: 565-583. |
| [12] |
曹俊武, 刘黎平, 葛润生. 模糊逻辑法在双线偏振雷达识别降水粒子相态中的研究[J]. 大气科学, 2005, 26(5): 768-778. |
| [13] |
T.A.Seliga, V.N.Bringi. Use of Polarization to Characterize Precipitation and Discrimination Large Hail[J]. J. Atmos. Sci, 1990, 7: 1525-1540. |
| [14] |
T.A.Seliga, V.N.Bringi. Potential Use of Radar Differential Reflectivity Measurement at Orthogonal Polarization for Measuring Precipitation[J]. J. App Metero., 1976, 15: 69-76. DOI:10.1175/1520-0450(1976)015<0069:PUORDR>2.0.CO;2 |
| [15] |
张培昌, 杜秉玉, 戴铁丕. 雷达气象学[M]. 北京: 气象出版社, 2001.
|
| [16] |
Brandes E A, Ikeda K. Freezing-level estimation with polarimetric radar[J]. J. App. Meteorlogy, 2004, 43(11): 1541-1553. DOI:10.1175/JAM2155.1 |
 2006, Vol. 32
2006, Vol. 32