2. 山西省气象局
2. Shaanxi Province Meteorological Bureau
由V.Vapnik等人提出的统计学习理论(Statistic Learning Theory, SLT)是一种小样本的机器学习理论[1, 2]。通过对学习一致收敛问题的讨论, SLT给出了不同于传统学习中经验风险最小化准则(Empirical Risk Minimization, ERM)的结构风险最小化准则(Structure Risk Minimization, SRM), 并在此基础上给出了一种新的学习算法——支持向量机(Support Vector Machines, SVM)。SVM通过非线性核函数, 将输入样本空间映射到一个高维乃至无穷维的线性特征空间, 构造样本空间的最优划分或回归线性超平面, 最优超平面的构造过程即是实现SRM准则的过程。SVM可以解决样本空间中的高度非线性分类和回归等问题, 是一种处理非线性分类和非线性回归的有效方法, 且其人为设定的参数少, 便于使用, 因而有着广阔的应用空间, 如在多文本识别、图像识别、信号处理、基因图谱识别等, 也为样本分析、因子筛选、信息压缩、知识挖掘和数据修复[3-5]等诸多方面提供了新的工具。
短期气候预测包含大量的非线性因素。传统的统计预报方法, 在建立预测模型时要求因子与预报对象间存在显著的线性相关, 且因子间要求线性相关达最小。而引起气候变化诸多因子的复杂性和非线性, 决定了预报因子与预报对象间的非线性相关, 因而传统的统计预报方法很难解决本质是非线性关系的气候预测问题。陈永义等[6, 7]将SVM引入了气象领域, SVM目前在气象上的应用主要是在短期天气预报、数值预报释用、实时短期预报业务[8-10]等方面, 本文尝试将SVM用于样本量小的短期气候预测。
1 支持向量机(SVM)的基本思想支持向量机的核心是支持向量(Support Vector, SV), 其基本思想是升维和线性化。即基于Mercer核展开定理, 通过非线性映射ϕ, 把样本空间映射到一个高维乃至无穷维的特征空间(Hilbert空间), 在特征空间中引入ε——不灵敏函数作为误差函数, 当所有样本点到所求超平面的距离都可以小于ε时, 寻求最优回归超平面的问题转化为求解一个二次凸规划问题, 并可以求得全局最优解, 使在特征空间中可以应用线性学习的方法解决样本空间中的高度非线性分类和回归等问题。
降维, 即向低维空间做投影, 是处理复杂问题常用的一种方法, 这样做可以降低计算的复杂性。升维, 即向高维空间做映射ϕ, 一般只会增加计算的复杂性, 甚至会引起“维数灾”。如何求得非线性影射和解决算法的复杂性, SVM巧妙地解决了这两个难题。由于应用了核函数的展开定理, 所以根本不需要知道非线性映射的显式表达式, 由于是在高维特征空间中应用线性学习机的方法, 所以与线性模型相比几乎不增加计算的复杂性。SVM正是基于这种思想, 将在低维样本空间无法线性处理的非线性分类、回归问题, 在高维特征空间通过一个线性超平面, 以实现线性分类、回归。
2 支持向量机在短期气候预测中的应用 2.1 SVM分类法在短期气候预测中的应用目前, 短期气候预测实际业务中主要是对月、季、年降水和气温的预测, 预测质量的评定采用分级评定, 实际业务中, 可以将大于某级临界值的预报对象归为+1类, 小于这一临界值的归为-1类, 然后选择因子, 确定核函数进行建模。对各级采用同样的方法进行分类预测, 进而得到预报对象的预测等级。
2.2 SVM回归法在短期气候预测中的应用利用SVM分类法对月、季、年的降水和气温进行分类预测, 需要对不同级的预报对象设定+1类和-1类, 其预报结果也只能是量级。采用回归法, 可以直接得出预报对象的预测值, 在具体操作上只是把分类法资料集上的第一列由+1或-1换为具体数值。可以用同样的资料进行两种方法的对比试验。
2.3 SVM短期气候预测实例 2.3.1 CMSVM简介CMSVM是中国气象局培训中心CMSVM开发组编制的, 它是在Windows平台下集训练学习、参数寻优、结果分析和预报等功能为一体的全中文应用软件平台, 能用于分类预报和回归预报, 适合解决高度非线性的分类和回归等问题。
2.3.2 用SVM进行阳泉夏季降水的预测 2.3.2.1 资料及资料处理选取1951—2004年共54年阳泉夏季6—8月降水量作为预报对象, 正距平的记为1, 负距平的记为-1。需要说明的是, 本文的主要目的是介绍支持向量机基本原理及其在短期气候预测中的应用尝试, 所以在分类预测试验时只是简单的将夏季降水划分为正、负距平(资料中为1、-1)建立分类预测模型, 实际业务工作应该根据不同的临界值建立分类模型并进行集成。
选择相应年份4月的nino1+2、nino3、nino4、nino3+4区海温, 1—4月南方涛动指数, 4月份西太平洋副热带高压面积指数、西伸脊点指数、亚洲区纬向环流指数、亚洲区经向环流指数、青藏高原B指数、印缅槽指数, 1月份亚洲区极涡面积指数共15个预报因子。并对每个因子进行归一化处理:(x-xmin) /(xmax-xmin)。
归一化处理有利于避免各个因子之间的量级差异, 使每一因子的数据均落入区间[0, 1], 整理好的分类预测资料形式为:

|
对回归预测资料, 需要将第一列数据换为原始值, 如下形式:

|
SVM建模时一般将总样本的75%分为训练样本, 用于训练学习建模, 20%分为实验样本, 用于进一步调整模型的参数, 5%分为检验样本, 用于预报检验。需要指出的是, 这一过程应该是随机的。本文中将40a的样本作为训练样本、10a作为实验样本、4a作为检验样本。
2.3.2.2 确定核函数由于构造向量机的基础是Mercer定理, 作为建立支持向量机的核函数必须以满足Mercer定理的条件为前提。对于非线性问题通常选用径向基函数或多项式核函数。本文以满足Mercer定理的径向基函数作为核函数建立阳泉夏季降水SVM分类模型。
2.3.2.3 构建训练集、实验集使用陈永义等开发的CMSVM, 可以很方便的建立SVM模型。具体步骤为:选定训练数据、实验数据、检验数据文件, 选定工作模式(分类、回归), 选定核函数, 选定相关参数及初始值、循环次数及步长, 计算机即会自动选择最优模型。
尽管选定径向基函数为核函数建立SVM模型, 但伴随参数选取的不同, 函数的形态也会发生相应的变化, 进而引起SVM模型的变化。在实际业务中, 应该进行大量的试验, 以选取最佳的参数组合, 使建立的SVM模型预测效果最好。
首先进行阳泉夏季降水SVM分类模型的训练、实验, 结果见表 1。
|
|
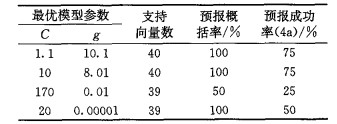
表 1 不同参数值对阳泉夏季降水SVM分类模型的影响 |
从表 1中可以看出, 不同的C、g组合对SVM模型有很大的影响, 选择好的参数, 可以使模型有较强的预报能力。前两种模型的预报概括率达到100%, 预报成功率为3/4。
又进行了阳泉夏季降水SVM回归模型的训练、实验, 回归择优标准用绝对差, 在参数C的初始值、循环值、步长分别为:100、10、10, 核参数g的初始值、循环值、步长分别为:0.001、10、0.01, 回归带宽参数w的初始值、循环值、步长分别为:0.001、10、10, 不敏感损失函数的上界设为2000, 回归迭代最大次数设为1000的情况下, 用187.34秒寻找到最优回归模型, 最优模型中的各参数的最优值为:C=190, w=60.001, g=0.091, 支持向量SV有24个, 其中19个在边界上, ε不敏感损失函数loss=1718.61664, 本次训练模型使用核函数进行计算的次数是:2689。
用最优模型对检验文件进行回归计算:绝对差=67.9282, 相关系数=0.952123, 均方差=89.9841。
对4a的预报检验情况见表 2。从表中可以看出无论趋势还是实际评分均正确。
|
|
表 2 阳泉夏季降水SVM回归模型预报检验情况 |
(1) SVM可以解决样本空间中的高度非线性分类和回归等问题, 是一种处理非线性分类和非线性回归的有效方法。
(2) 利用SVM建立短期气候预测模型时, 应着重从有物理意义的因子中选择预报因子, 而不需要过多考虑预报因子与预报对象的线性相关关系。
(3) SVM作为一种数据挖掘技术, 可以从海量的信息中提取关键样本, 即支持向量, 因而, 预报因子中包含的有效信息越多, 所建立的预测模型越能描述预报对象的时空特征。
(4) SVM在短期气候预测中可以用于非线性分类预报和非线性回归预报, 具有较强的预报能力。
(5) 在进行模型训练、实验时, 需要对C、g、w等参数的初始值、循环值、步长进行调试, 带有一定的人为性, 不同的参数组合对SVM结果有很大的影响。
(6) 本预报效果只是一次随机实验, 更可靠的效果分析有待于作交叉验证。
| [1] |
Ratsaby. Incremental learning with sample queries[J]. IEEE Transactionson Pattern Analysis and Machine Intelligence, 1998, 20(8): 883-888. DOI:10.1109/34.709619 |
| [2] |
Wang E H C, Kuha. Asmartalgorithm for incremental learning[C]. International Joint Conference on Neural Networks, 1992, 3: 121-126. https://www.mendeley.com/research-papers/smart-algorithm-incremental-learning/
|
| [3] |
杨晓懿, 刘嘉勇, 陈淑敏. SVM在文本自动分类中的应用[J]. 成都信息工程学院学报, 2005, 20(2): 121-124. |
| [4] |
孟继成, 杨万麟. 基于核函数的雷达一维距离像目标识别[J]. 电子与信息学报, 2005, 27(3): 462-466. |
| [5] |
张辉, 张浩, 陆剑锋. SVM在数据挖掘中的应用[J]. 计算机工程, 2004, 30(6): 7-8. |
| [6] |
陈永义, 俞小鼎, 高学浩, 等. 处理非线性分类和回归问题的一种新方法Ⅰ——支持向量机方法简介[J]. 应用气象学报, 2004, 15(3): 345-353. |
| [7] |
冯汉中, 陈永义. 处理非线性分类和回归问题的一种新方法(Ⅱ)——支持向量机在天气预报中的应用[J]. 应用气象学报, 2004, 15(3): 355-364. |
| [8] |
冯汉中, 陈永义. 支持向量机回归方法在实时业务预报中的应用[J]. 气象, 2005, 31(2): 41-44. |
| [9] |
车怀敏. 用支持向量机方法作德阳降水预报[J]. 四川气象, 2005(2): 13-15. |
| [10] |
冯汉中, 杨淑群, 刘波. 支持向量机(SVM)方法在气象预报中的个例试验[J]. 四川气象, 2005(2): 9-12. |
 2006, Vol. 32
2006, Vol. 32