2. 兰州大学中德干旱环境联合研究中心;
3. 中国人民解放军 93920 部队
2. Center for Arid Environment and Paleoclimate Research, Lanzhou University;
3. Unit 93920, PLA
获取某些物理量在特定区域内的平均值在研究领域是非常有意义的。比如针对于某个区域空间建立平均温度序列; 对流域内某个时段的平均降雨量进行计算, 可以对洪峰进行定量的分析和预报, 进而合理地进行洪水调度, 减少洪灾损失。
此前, 求解物理量区域平均的计算方法有大量研究, 比如积分法[1], 泰森多边形法[2]、逐步订正格点法[3]、三角形法[4]、算术平均法、格点插值计算法[5]、Barne s法[6], 等雨量线法[7]等。但是由于观测站点分布不均, 使得面平均物理量的计算并不简单, 而且完全真实地反映实际情况几乎不可能做到。因此应该去探索各种不同的计算方法, 在实际运用时才能进行多方比较, 最终得到一个与真实情况更接近的计算结果。
1 常用的计算方法介绍求解物理量空间平均的具体计算方法在引言中进行了列举, 这些计算方法大致可以归纳为以下几类:(1)直接建立非规则的网格。比如泰森多边形法[2], 该方法的权重面积是由各相邻两站间连线的中垂线构成的多边形。(2)建立规则化的网格面。将研究区域划分为规则的网格, 通过插值使得网格中的各个单元获取与之相邻站点的观测信息, 再进行分析计算。(3)等值量线法。先填绘等值线, 然后再确定权重系数的方法。(4)积分计算。通过对研究区域内分散的站点测量值进行分析, 寻找一个能够尽量反映该物理量的分布函数f(x, y), 然后通过二重积分进行计算。
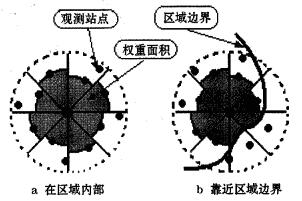
2 一种新的权重面积构想 2.1 权重面积的设计在研究区域内部的某个站点, 此站点以m个等扇面向外扩张, 当它遇到区域内的其他站点时被终止, 最后围绕着这个站点就可以形成一个由m个扇形组合起来的领域(如图 1a); 如果站点靠近边界, 那么有的等扇面在向外扩张的时候被边界挡住, 最后则形成以边界和邻近站点合力包围的领域(如图 1b)。由于站点密集的地方包围面积小, 站点稀疏的地方包围面积大, 所以上述设计的包围面积可以用来作为加权平均时的权重面积。
|
图 1 用扇形组合构成权重面积示意图 |
假设研究区域内有n个站点, 而且第j个站点的权重面积为sj, 那么对于某物理量A在区域内的加权平均值为:
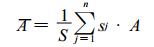
|
其中S为所有观测站点的权重面积之和: S 
sj的确定方法:假设第j个站点的m个子区域中第i个子区域内受阻挡的弧线或者边界与扇形的两边围成的扇面面积为σi, 那么第j个研究站点的权重面积为:
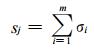
|
由于研究站点的扇形子区域会出现两种情况:子区域内有一个以及一个以上的观测站; 子区域内没有其他观测站。因此对于每个子区域所贡献的σi的计算分为两种情况:
(a)子区域内有其他测站
假设第i个子区域内有η个观测站, 它们与研究站点之间的距离分别为r1, r2, …, rη, 其中第k个观测站与研究站点的距离最近, 即:
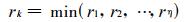
|
定义该子区域对研究站点所贡献的权重面积分量为:
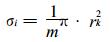
|
(b) 子区域内没有测站
子区域内没有观测站, 则在把该子区域用θ条射线再等分成个更细小的区域, 其中第l条射线与边界相交所得的线段长度为rl, 则该子区域对研究站点所贡献的权重面积分量为:
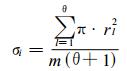
|
显然θ越大误差越小, 但是计算量越大。
3 对数学模型的检验及分析站点的位置是固定的, 当研究区域选定后, 上述数学模型中只有参数可以变化。如果随着m的变化计算结果不稳定, 说明所设计的权重面积用来加权平均是失败的, 因此有必要对m进行检验。此外在资料不全的情况下也进行了计算, 讨论该方法对于部分资料缺失时的自动插补功能。
3.1 选取的资料及其计算方法选取35° N以北、110° E以西的中国境内1961—2001年所有地面气象站的观测降雨量资料和区域内的28个探空站1983—1998年的探空资料。
计算方法是:先计算出各个气象站的多年平均降雨量和水汽含量, 然后用上述方法, 取不同的值, 计算区域内的多年平均年降雨量和水汽含量。资料缺失的方法是每读入4个站的资料后就跳过一个站, 也就是说在完整资料的基础上缺失了20 %的观测站点。
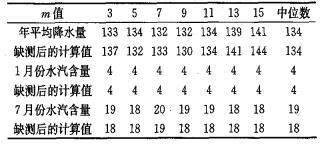
3.2 计算结果和分析计算结果见表 1。从表中可以看出取不同值时, 运算结果比较稳定(相对误差小于5 %); 此外, 在资料的缺失程度达到20 %的情况下, 用该方法计算出的各物理量区域平均值并没有多大变化, 说明该方法在部分资料缺失时也有较好的适用性。下面对该数学模型的稳定性和资料缺失时的适用性进行分析。
|
|
表 1 取不同的m值所得到的均值情况(单位:mm) |
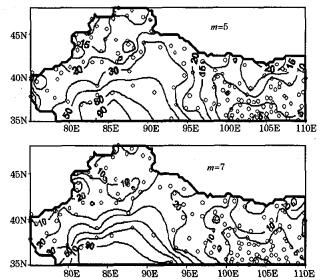
为了分析权重面积与站点疏密之间的关系, 分别将m=5, m=7两种情况下, 各站点权重面积绘制出等值线图(见图 2)。从图 2中可以看出:当观测站点密集的地方权重面积小(如105° E附近), 观测站点稀疏的地方权重系数大(如90° E附近)。此外, 虽然m的取值不同, 但是权重面积的分布情况很相似, 这就是运算结果比较稳定的原因。
|
图 2 m取不同值时权值面积百分比与站点分布状况图 |
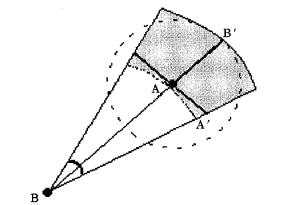
假设站点A就是一个资料缺失的站点, 站点B是A的邻近站点之一(见图 3), 它们之间的距离为d; B′是BA延长线与A站点权重面积圆的交点; A′A⊥AB。把观测站点的权重面积近似地看作是以该站点为圆心的圆形, 那么当站点存在时站点的权重面积为:
|
图 3 扇面扩充示意图 |

|
A站点缺失后, 以前被A站点阻挡的那个扇面又向前推进了rA才会碰到其他站点而被阻止(rA=AB′, 是A站点所拥有的权重圆的半径, 因为站点位置是固定的, 所以rA是一个常数), 此时站点A的控制面积将会增加δs(图 3中的阴影部分就是δs, 其中∠ABA′=π/m, AB=d, AB′=rA, AA′=tg(π/m)·d), 其近似值为:
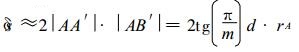
|
权重面积的增长百分比为:
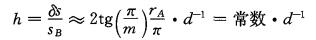
|
从上式可以看出:当站点A缺失时, 周边B站点的权重面积增长百分比与两者之间的距离成反比。所以某个站点缺失时, 缺失站点控制的区域被周边的几个站点以变相的距权反比方式进行了插值, 距离越远的站点影响越小。这种变相的插值过程不但能排除外围站点的影响, 而且能保证影响站点来自不同的方向, 因而该方法在资料不全的时候计算结果具有较好的可信度。
3.3 对比检验限于篇幅只选择算术平均、泰森多边形法[8]、格点插值计算法的计算结果与文中设计的方法进行比较。通过以上的计算对同一组物理量得到了4组不同的值(见表 2)。
|
|
表 2 四种不同的方法计算出的均值比较 |
从表 2中可以看出, 用扇形组合而成的权重面积进行加权平均计算物理量的面平均值是可行的。而且该方法具备泰森多边形法保证原始观测数据不变的优点; 同时在有缺测站点的时候能够自动插值, 计算结果受缺测站的影响较小; 此外, 容易实现电算, 而且计算量较小。
| [1] |
常安定, 周明. 面平均雨量的积分计算[J]. 西安工程学院学报, 1998, 20(4): 63-65. |
| [2] |
王铭才. 大气科学常用公式[M]. 北京: 气象出版社, 1994: 518-519.
|
| [3] |
孟遂珍, 彭治班, 赵秀英, 等. 流域平均降水量的一种算法[J]. 北京气象学院学报, 2001(2): 64-68. |
| [4] |
董官臣, 冶林茂, 符长锋. 面雨量在气象预报中的应用[J]. 气象, 2000, 26(1): 9-13. DOI:10.7519/j.issn.1000-0526.2000.01.002 |
| [5] |
刘小虎, 赵雅贤, 杨鹏. 利用网格插值算法计算流域面平均降雨[J]. 海河水利, 2003(3): 45-46. |
| [6] |
Barnes S L. A technique for maximizing details in numerical weather map analysis[J]. J.Appl.Met., 3: 396-409. DOI:10.1175/1520-0450(1964)003<0396:ATFMDI>2.0.CO;2 |
| [7] |
倪天倪, 丁琴, 万定生, 等. 非线性等雨量线生成系统KRIGS的算法与设计[J]. 河海大学学报, 1995, 23(2): 45-49. |
| [8] |
汤成友. 计算机求解泰森多边形权重的方法[J]. 四川水利, 2002(3): 40. |
 2006, Vol. 32
2006, Vol. 32