2. 西藏山南地区气象局
2. Shannan Meteorological Observatory, Tibet
近年来很多研究发现青藏高原(以下简称高原)地表温度的变化与我国众多地区的后期降水和地震等现象具有密切的关系。柏晶瑜等[1, 2]指出高原地温的异常对长江中下游和四川盆地夏季降水异常具有“强信号”的指示作用。李超[3]通过研究高原0.8地温与我国汛期降水的关系发现高原秋季地温与我国汛期降水存在着负相关, 地温异常的位置与降水场的关系非常密切。目前又有研究表明浅层地温的异常偏高对高原的地震指示作用同样非常显著[4]。
然而目前针对高原地温自身变化特征的研究比较少[5, 6], 因此在文献[6]的研究基础上, 进一步研究高原地表温度的空间异常分布和时间演变规律是必要的, 可为地温的后期预测提供科学依据。
1 资料和方法本文选取了分布在青海省和西藏自治区区域内的40个气象观测站1970 ~ 2002年33年月平均0cm地温(以下简称地温)资料。在进行EOF展开之前首先对该资料做标准化处理, 这是为了消除测站地理位置和月际差异影响[7, 8]。这样, 每站的方差变为1, 场的总方差为40。使得EOF的结果更适合作分类分型分析[9]。利用二阶多项式和小波分析分别研究了高原各分区代表站地温随时间的变化特征和周期特性。
2 高原年平均地温的空间异常特征及分布表 1给出前8个特征向量的方差贡献。由表 1可见, 前8个特征向量的方差贡献率达82.6 %, 第一特征向量的方差贡献占总方差的46 %, 前三项占64.4 %, 且根据North等[10]人提出的检验特征值的准则得到前三个特征根所对应的EOF是有价值的信号, 所以选取前3个特征向量分析高原地温分布的空间特征是有意义的。
|
|
表 1 前8个EOF分量对场总方差的贡献 |
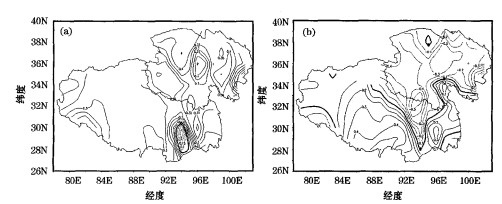
图 1a为高原年平均地温第一特征向量场, 虽然在雅鲁藏布江下游出现了负值, 但负值的范围和强度都很小, 不足-0.2而高原绝大部分为正值, 高值区位于柴达木盆地的格尔木、大柴旦, 黄河和湟水流域的都兰, 祁连山一带的兴海。此特征向量反映了高原地温变化的一致性, 可见高原虽然地形复杂、地势参差不齐, 高山、草原、湖泊和河流纵横交错, 但高原受大尺度天气、气候系统影响是事实。
|
图 1 青藏高原年平均地温的第一(a)、第二(b)特征向量场 |
夏季高原喜马拉雅山南麓和雅鲁藏布江流域深受印度季风的影响, 而高原北部处于我国季风影响的边缘区, 季风影响不明显; 冬季高原主体及其北部是冷空气影响我国的主要门户之一, 此时由于受高原北部东西走向大山脉的阻挡作用, 冷空气无法长驱直入影响雅鲁藏布江流域和喜马拉雅山南麓地区, 这就是第二特征向量场反映出的高原年平均地温的南北差异(图 1b)。
众所周知, 高原主体多高耸的山脉, 而高原南北分别处于雅鲁藏布江谷地和广阔的柴达木盆地, 后者地势起伏较小, 且海拔高度相对主体而言较低, 高原年平均地温第三特征向量场(图略), 正是反映出了地温分布在高原主体与北部和南部之间的差异, 即高原北部和南部的雅鲁藏布江流域为正值, 其中心分别位于高原北部的诺木洪和南部的泽当, 而高原主体为负值区, 中心位于沱沱河一带。所以可以看出海拔高度和地形对高原地温的分布具有制约作用。这与文献[5, 6]的论断相吻合。
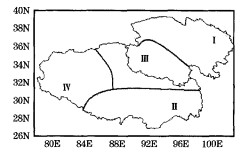
根据高原年平均地温的EOF展开所得到前三个特征向量场, 可以将高原年平均地温场分为以下几种分布型, 即东北部型、南部型、主体型和西部型(图 2)。各型所包含的站点和代表站具体如下:
|
图 2 青藏高原年平均0cm地温的分区 |
东北部型包括托勒、祁连、大柴旦、德令哈、门源、格尔木、诺木洪、都兰、察卡、恰卜恰、西宁、贵州、民和、兴海、河南、班玛、同德、久治, 代表站是诺木洪。
南部型包括日喀则、江孜、尼木、拉萨、当雄、泽当、浪卡子、隆子、错那、林芝、波密、察隅, 代表站是泽当。
主体型包括沱沱河、玉树、那曲、昌都、丁青、安多、索县、囊谦, 代表站是沱沱河。
西部型包括改则、普兰、狮泉河, 代表站是普兰。
3 高原年平均地温的时间变化特征由于各分区的代表站是特征向量场中的最大荷载值所在点, 所以利用代表站30年的地温变化特征可以比较好地反映各分区的地温变化特征。
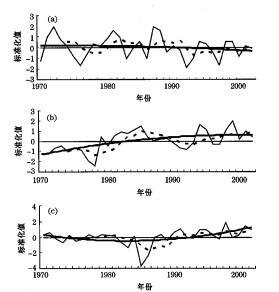
图 3a是高原东北部代表站诺木洪地温的变化特征, 由二阶多项式变化曲线可见在近30年里高原东北部地温总的趋势是呈下降的, 即在20世纪80年代中期以前处于高地温期, 之后处于降温期, 目前高原东北部的地温仍处于较低的态势。
|
图 3 高原各分区代表站地温标准化值 a.诺木洪 b.泽当 c.沱沱河 细实线为地温标准化曲线、粗实线为二阶多项式曲线、点线为地温标准化的5年滑动平均 |
高原南部的代表站泽当的地温(图 3b)变化趋势反映了高原南部在20世纪80年代中期之前处于低地温期, 之后逐渐增温, 进入80年代中期之后处于高地温期, 而且这种增温趋势一直持续到现在。即高原南部地温仍处于增温期。
由高原主体代表站沱沱河年平均地温变化特征(图 3c), 清楚地反映出在近30年的时间中高原主体地温经历了高—低—高的抛物线型变化过程, 即在20世纪70年代中期之前处于高地温期, 而70代末到80年代近10年的时间里高原主体处于低地温期, 90年代初地温开始逐渐回升, 并进入了高地温期。
高原西部的普兰站年平均地温变化特征(图略)反映了高原西部地温在近30年的时间里同样经历了地温变化的高—低—高的抛物线型变化过程, 目前该区域处于高地温期。不难看出高原主体和西部地温变化特征较相似, 这可能是由于这两区域都是高原平均海拔高度最高的区域, 而且部分下垫面性质也比较相似的缘故。
4 高原年平均地温的周期特征由于小波分析对信号处理的特殊优势, 近几十年来许多气象学家都将其用于气象和气候序列的时频结构分析中, 并取得了许多可喜的研究成果[8, 11]。以下分别对高原地温分布的东北部、主体、南部和西部型, 进行小波周期分析。
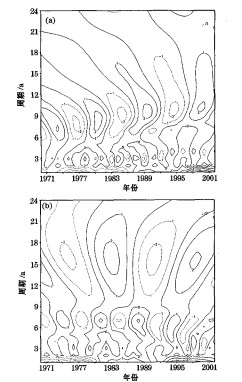
图 4a是高原东北部型年平均地温Morlet小波分析, 在过去的近30年高原东北部年平均地温年际变化始终存在着3a振荡周期, 这种3a的周期与青藏高原气温的年际变化的准3年周期变化相一致。可见高原地表温度温和空气温度的变化具有同步变化趋势。另外, 高原年平均地温存在着准7年的振荡周期。
|
图 4 青藏高原各分区年平均地温Morlet小波系数时-频分析图 a.东北部 b.南部 |
从图 4b来看, 高原南部的雅鲁藏布江流域地温具有3a和准7a的振荡周期。准3a的周期不仅与高原空气温度周期相一致, 而且与青藏高原降水和高原季风的周期相一致, 可见雅鲁藏布江河谷地温的变化不仅受到了空气温度、降水的影响, 而且受印度季风的制约, 或者说高原地温的变化也将影响到高原降水和季风的开始、结束以及强度。另外, 雅鲁藏布河谷的地温还存在着14a的年代际的周期, 20世纪80 ~ 90年代尤为明显。
高原主体和西部的年平均地温在近30年里也同样存在着3年和准7年的周期变化特征(图略), 其中高原主体存在着准12年的年代际振荡周期。
综上所述, 青藏高原年平均0cm地温的变化是由各个时间尺度周期、准周期的叠加而成的。而且这种周期与各种气象、天文等因子的多尺度变化周期相接近。如3年的周期不仅与高原降水、气温、季风、地面加热场、ENSO现象的周期相一致, 而且还与地球自转速度的准3 ~ 4年的天文周期和西太平洋副热带高压活动的周期相近[12]; 而准7年振荡还与长江中下游、华北地区、云南、内蒙古等地的汛期降水的周期相一致。由此看出青藏高原年平均地温的变化不仅受到高原季风、降水、ENSO以及大尺度环流的演变的影响, 而且其异常变化可能是中国众多区域的汛期降水异常的“强信号”[1~3]。
5 结论(1) 青藏高原年平均地温第一特征向量场为一致的正值, 揭示了高原受大尺度天气系统影响的事实; 第二特征向量场为南正北负, 反映了高原南部和北部的差异; 第三特征向量场为高原主体和南、北部的差异, 揭示了地形对高原地温分布的影响。
(2) 高原年平均0cm地温空间异常可分为4个气候区, 即东北部、南部、主体和西部。
(3) 近30年里, 高原东北部20世纪80年代中期之前处于高地温期, 之后开始降温直到目前; 而高原南部80年代中期之前为低地温期, 之后地温开始上升目前处于暖地温期; 高原主体和西部地温变化具有高—低—高的抛物线型, 即在70年代中期之前处于高地温期, 之后直到90年代初处于低地温区, 从90年代中期开始地温逐渐回升并进入高地温期。
(4) 青藏高原各分区地温具有比较一致的变化周期即3a和准7a的振荡; 高原南部和主体分别具有14a和12a的年代际振荡周期而高原东北部和西部无明显的年代际振荡周期。
| [1] |
柏晶瑜, 徐祥德. 1998年青藏高原春季地温异常对长江中下游夏季暴雨影响的研究[J]. 应用气象学报, 1999, 10(4): 478-485. |
| [2] |
陈忠明, 闵文彬, 刘富明. 青藏高原地表热源异常与四川盆地夏季降水的关联[J]. 气象, 2003, 29(5): 9-12. DOI:10.7519/j.issn.1000-0526.2003.05.002 |
| [3] |
李超. 青藏高原0.8地温异常与我国汛期降水的关系[J]. 成都气象学院学报, 1995, 10(2): 175-181. |
| [4] |
刘小凤. 青藏高原北部浅层地温异常特征及中短期地震预测[J]. 高原地震, 2002, 14(2): 1-7. |
| [5] |
戴加洗. 青藏高原气候[M]. 北京: 气象出版社, 1990: 171-196.
|
| [6] |
李栋梁, 吴青柏, 汤懋苍. 青藏高原地表 0cm温度的时空变化特征[J]. 科技导报, 2005, 1: 18-22. |
| [7] |
吴洪宝, 李栋梁, 章基嘉. 中国冬季月平均气温异常的旋转EOF分析[J]. 南京气象学院学报, 1995, 18(3): 349-354. |
| [8] |
李栋梁, 姚晖. 中国西北夏季降水量与500hPa纬偏场的特征分析[J]. 气象, 1995, 21(11): 22-26. DOI:10.7519/j.issn.1000-0526.1995.11.005 |
| [9] |
魏凤英. 现代气候统计诊断与预测技术[M]. 北京: 气象出版社, 1999.
|
| [10] |
North G.R.T, Cahalan Bell.R., Moeng F.J. Sampling errors in the estimation of empirical orthogonal function[J]. Mon.Wea.Rev, 1982, 110: 699-706. DOI:10.1175/1520-0493(1982)110<0699:SEITEO>2.0.CO;2 |
| [11] |
林振山, 邓自旺. 子波气候诊断技术的研究[M]. 北京: 气象出版社, 1999.
|
| [12] |
杨鉴初, 史久恩. 我国长期天气预报的进展[J]. 气象, 1979, 5(10): 4-7. DOI:10.7519/j.issn.1000-0526.1979.10.002 |
 2006, Vol. 32
2006, Vol. 32 