干旱是危及人类生存环境的严重问题, 日益成为人们关注的热点, 王志伟等用Z指数作为等级划分标准, 得到了我国北方干旱逐月变化特征[1]; 孙凤华等利用GM(1, 1)模型探讨了辽宁省旱灾预测问题[2]; 顾润源等指出冬季大气环流、北太平洋SST对山东夏季旱涝趋势的预测具有重要指示意义[3]; 王劲松等对甘肃省河西地区径流量干旱指数[4], 张春桂等对福建省干旱灾害卫星遥感监测应用进行了研究[5], 均得到了具有实用价值的研究成果。
渭河流域地处我国西北地区东部生态环境脆弱带, 自然灾害多有发生, 在众多自然灾害中, 以旱灾发生最为频繁, 程度最重, 危害最大, 成为制约国民经济特别是农业经济和农业持续发展长期的、主要的因素。本文运用负轮理论和游程理论分析渭河流域降水丰枯转移概率及连续丰、枯年的分布特点; 引入马尔可夫平稳概率研究干旱发生的自然属性, 以干旱强度、干旱周期、丰枯转移概率等指标, 全面刻画渭河流域的干旱特征, 并根据渭河流域12个站点1958~2001年的天然径流量、降水量和气温资料建立起了适用于渭河流域的S干旱指数。
1 渭河流域干旱特征 1.1 降水丰枯参数受地形等因素影响, 流域降水分布由东南向西北递减, 南岸秦岭山麓降水充沛, 最大年降水量在1000mm以上, 随地势降低降水量骤减, 平原河套地区年降水量约为500mm。
从渭河流域各典型站点降水丰枯频率(表略)分析可知, 流域多年平均降水量在437~665mm之间, 降水变率为16%~22%, 变差系数Cv值为0.21~0.28;少水出现的频率最大, 各站都在50%以上。以多年平均降水量P作为阈值, 大于P的为多水年, 否则为少水年, 具体又划分为4个级别, 枯水级:P≤P-σ, 偏枯级:P-σ<P≤P, 偏丰级:P<P≤P+σ, 丰水级:P>P+σ。其中σ为年降水量的均方差。从4个降水等级出现的频率来看, 偏枯年出现的平均频率最大, 为36.9%;其次是偏丰年, 平均频率为29.1%, 然后是枯水年。平均频率为17.7%;最后是丰水年, 平均频率为16.3%。渭河流域枯水年发生的频率多在15%以上, 说明该地区容易发生干旱。
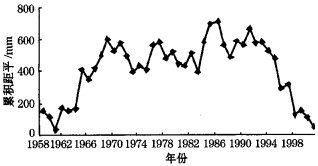
图 1为渭河流域年平均降水量累积距平曲线, 从图中可以看出上升段和下降段持续时间较长, 反映丰水和枯水连续性较强, 说明连丰或连枯的概率较大。由于降水过程的随机性及年际变化的复杂性, 从原始降水数据资料也可以分析得到, 渭河流域降水过程有丰水年和枯水年交替出现的周期性现象。
|
图 1 渭河流域年平均降水量累积距平曲线 |
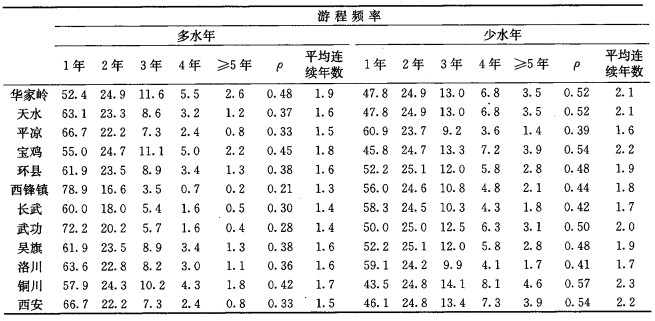
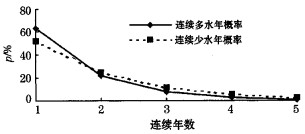
表 1为用游程理论分析的渭河流域连续多水(少水)年概率。从中可以看出, 渭河流域多(少)水期多持续2~3年, 持续4~5年的概率较小; 单独多(少)水年出现的概率比连续多水(少水)年的概率大; 单独多水年的概率比单独少水年的概率高; 而连续多水(少水)年出现概率的情况则正好相反, 连多出现的概率比连少出现的概率低(见图 2)。游程理论概率模型分布参数ρ值反映了出现连续状态概率的大小, 表 1中, 各站ρ少水年概率均大于ρ多水年概率, 可以反映出连少年的概率比连多年的概率大; 各站平均连续少水年数也均大于平均连续多水年数。
|
|
表 1 渭河流域连续多水年和少水年游程分析 |
|
图 2 连续多水年、少水年概率比较 |
马尔可夫链模型是以概率论为基础, 对平稳随机现象用自回归过程方法进行定量预测的模型, 用下面的矩阵来表示:
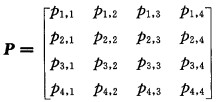
|
(1) |
脚标含义:1为枯水, 2为偏枯, 3为偏丰, 4为丰水。
把P矩阵分为三个小矩阵来研究:

|
(2) |
PPA是反映偏枯、偏丰平稳的转移过程, 对用水有利; PPB是反映枯(丰)水与偏丰(偏枯)之间的小突变, 对用水可能带来不利影响; PPC是反映丰枯水之间的变化, 多会发生洪水或旱灾, 可视为突变[6]。
将各站转移矩阵按上述三个矩阵各项相加可得表 2, 从中可以看出本研究所选择的渭河流域12个典型站有1/3的站点PPB超过了50%, 所有的站点PPB都在40%左右, 说明枯(丰)水与偏丰(偏枯)之间的转移突变较大, 对用水可能带来不利影响。
|
|
表 2 渭河流域气象干旱平稳概率分布 |
按照1.1中划分的四个降水级别, 将渭河流域1958~2001年平均降水序列划分为涝、偏涝、偏枯、枯4种(对应于马氏链有4个状态)。以相依性最强的、步长为1的马尔可夫链的特征为例进行分析。
可以得到:
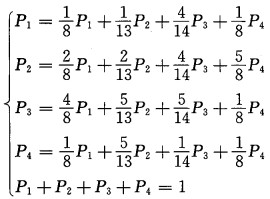
|
(3) |
由式(3)可以求出极限分布为:P1=0.166, P2=0.303, P3=0.346, P4=0.185。根据公式Ti=1/Pi, 则各状态的重现期分别为:T1=6.0(年), T2=3.3(年), T3=2.9(年), T4=5.4(年)。
根据上面的数据结果分析可知, 渭河流域近44年来的降水过程中, 偏枯年出现的概率最大, 为0.346, 平均3年出现一次; 偏丰年次之, 出现概率为0.303, 平均3.3年出现一次; 然后是枯水年, 出现概率为0.185, 平均5.4年出现一次; 丰水年最小, 平均6年出现一次。按照这一结果, 1958~2001年这44年中, 渭河流域涝年、偏涝年、偏枯年和枯水年出现的次数分别为7.3年、13.3年、15.2年、和8.1年, 根据划分的渭河流域降水量状态可知, 涝年、偏涝年、偏枯年和枯水年出现的实际次数分别为8年、13年、14年和8年。可见, 所得的结果基本与实际情况相符, 并且这一结果与1.1中的分析结果相一致。
1.4 干旱强度分析本文应用负轮理论分析渭河流域2~3年连续枯水年及最长连续枯水年的干旱强度(表略)可知, 渭河流域典型站连续2~3年少水的频率在3~7次之间, 平均降水亏缺量占多年平均降水量的10%~22%, 年最大降水亏缺量占多年平均降水量的26%~45%。渭河流域干旱连续最长一般为4~5年(天水站为8年), 最长连续枯水年年平均降水亏缺量占多年平均量的7%~29%, 年最大降水亏缺量约占多年平均降水量的8%~49%, 由此可见, 渭河流域连续2~3年少水不仅发生频率较高, 而且干旱强度也较大。
2 渭河流域干旱指标计算方法影响流域径流量变化的主要因素是降水和气温, 而径流量的丰枯变化则是衡量流域干旱情况的重要指标。王云璋等和王国庆等在对黄河中上游降水与径流、水资源与气候变化之间的关系进行分析时, 分别得到黄河中游年径流量与降水量存在显著的函数关系, 径流量丰枯还较明显的受同期气温的影响[7, 8]; 康玲玲等研究得到在降水不变的情况下, 渭河流域径流量较为明显的受到同期气温变化的影响[9]。
根据上述分析, 由降水指数和气温指数两部分组成的干旱指数描述渭河流域的干旱将更为合适, 本文参照康玲玲等在研究黄河中游干旱时使用的方法[9]作为渭河流域干旱的研究方法, 公式如下:
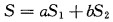
|
(4) |
其中:a, b为权重系数; S1为降水指数, 为了使降水指数和气温指数对干旱的贡献保持一致, S1的计算公式为:
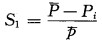
|
(5) |
S1的值有正、负之分, 分别表示对干旱的正、负贡献; S2为气温指数, 其公式为
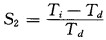
|
(6) |
Ti为逐月或逐年平均气温, Td为历史最低月或年平均气温, S2均为正值, 表示对干旱的正贡献。
本研究利用渭河流域的降水指数、气温指数和天然径流量资料, 利用SPSS统计分析软件中的偏相关分析方法来确定a、b的值。偏相关系数是衡量任何两个变量之间的关系, 而使与这两个变量有关的其他变量都保持不变, 根据观测资料应用偏相关系数, 可以判断自变量对因变量的影响大小。
表 3为渭河流域径流与降水指数、气温指数的偏相关分析结果, 从中可以看出降水指数和气温指数对径流的显著性水平均小于1%, 表示具有极显著的相关关系, 降水指数与径流的相关系数为-0.6748, 温度指数与径流的相关系数为-0.4866, 说明降水指数对渭河流域干旱的影响要大于气温指数的影响, 把两指数对应的相关系数的相对比例作为各自指数的权重系数, 分别为0.582和0.418, 所以渭河流域的S指数为:
|
|
表 3 渭河流域天然径流与降水指数、气温指数的偏相关分析 |
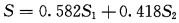
|
(7) |
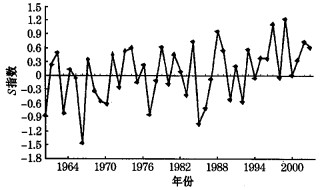
S值为正值时, 数值越大说明该年份越干旱; S值为负值时, 数值越小说明该年份水资源越丰沛。图 3为根据公式(7)和1958~2001年气温指数和降水指数得到的渭河流域S指数。从图中可以看出, S > 0的年份明显多于S < 0的年份, 20世纪90年代以后, 绝大部分年份的S值都位于图的上半部, 并且近44年来S值最大时所对应的年份也在90年代, 说明渭河流域的干旱状况有频率逐渐增加, 强度逐渐增大的趋势。用图 3与渭河流域1958~2001年实际旱涝情况对照, 所得结果基本相符, 所以S指数适用于对渭河流域干旱进行研究。
|
图 3 渭河流域S指数时间序列 |
本文运用游程分析、马尔可夫平稳概率、负轮理论, 结合渭河流域典型站1958~2001逐年平均降水量资料, 分析了研究区的干旱特征; 同时根据降水和同期气温、天然径流量资料建立了适用于渭河流域的S干旱指数。根据研究结果, 可以得到以下几点初步结论:
(1) 渭河流域容易发生干旱;
(2) 流域多(少)水期多持续2~3年, 单独多(少)水年出现的概率比连续多水(少水)年的概率大, 单独多水年的概率比单独少水年的概率高, 而连续多水(少水)年出现概率的情况则正好相反, 连少出现的概率比连多出现的概率高, 平均连续少水年数也均大于平均连续多水年数;
(3) 渭河流域偏枯年出现的概率最大, 为0.346, 平均3年出现一次; 偏丰年次之, 然后是枯水年, 丰水年最小, 平均6年出现一次;
(4) 流域连续少水2~3年不仅发生频率较高, 而且强度也较大;
(5) 根据以往的研究结果, 渭河流域的径流量较为显著的受到同期降水量和气温的影响, 本研究建立了以降水指数和气温指数两部分组成的S干旱指数用以描述渭河流域的干旱情况, 结果表明S值大于0的年份明显多于S值小于0的年份, 20世纪90年代以后, 绝大部分年份的S值都为正值, 并且近44年来S值最大时所对应的年份也在90年代, 说明渭河流域的干旱状况有频率逐渐增加, 强度逐渐增大的趋势, 所得研究区旱涝状况与流域1958~2001年的实际旱涝情况基本相符, 所以S指数适用于对渭河流域干旱进行研究。
| [1] |
王志伟, 刘文平, 王红霞. 我国北方干旱逐月变化特征分析[J]. 气象, 2005, 31(1): 37-40. DOI:10.7519/j.issn.1000-0526.2005.01.008 |
| [2] |
孙凤华, 袁健. 辽宁省近50年降水序列变化规律及干旱预测[J]. 气象, 2004(6): 32-34. DOI:10.7519/j.issn.1000-0526.2004.06.007 |
| [3] |
顾润源, 汤子东. 2002年夏季山东干旱成因分析[J]. 气象, 2004, 30(8): 22-26. DOI:10.7519/j.issn.1000-0526.2004.08.005 |
| [4] |
王劲松, 冯建英. 甘肃省河西地区径流量干旱指数初探[J]. 气象, 2000, 26(6): 3-7. DOI:10.7519/j.issn.1000-0526.2000.06.001 |
| [5] |
张春桂, 李文. 福建省干旱灾害卫星遥感监测应用研究[J]. 气象, 2004, 30(3): 22-26. DOI:10.7519/j.issn.1000-0526.2004.03.005 |
| [6] |
蔡明科, 粟晓玲. 黄土高原水文干旱特征分析[J]. 西北水资源与水工程, 2002, 13(4): 18-23. |
| [7] |
王国庆, 王云璋, 尚长昆. 气候变化对黄河水资源的影响[J]. 人民黄河, 2000, 22(9): 40-43. |
| [8] |
王国庆, 王云璋, 康玲玲. 黄河上中游径流对气候变化的敏感性分析[J]. 应用气象学报, 2002, 13(1): 117-121. |
| [9] |
康玲玲, 张亚民, 王玲玲, 等. 黄河中游干旱指数计算方法探讨[J]. 人民黄河, 2004, 26(8): 31-33. |
 2006, Vol. 32
2006, Vol. 32