2. 湖南省气象台, 长沙 410118;
3. 中国气象科学研究院, 北京 100081;
4. 湖南省气象服务中心, 长沙 410118
2. Hunan Meteorological Observatory, Changsha 410118;
3. Chinese Academy of Meteorological Sciences, Beijing 100081;
4. Hunan Meteorological Service Center, Changsha 410118
气温是水文学、气象学、地球系统科学领域中最关键的地表变量之一,与气候变化、自然灾害以及人类健康密切相关,当前政府以及公众对于精细化网格气温预报需求日益提升,要求获取具备空间无缝性和时间连续性的天气预报产品(刘新伟等,2020)。现代天气预报主要建立在数值预报模型基础之上,然而大气、海洋及其耦合系统运动常呈现非线性不稳定特征,数值模式尚不能很好刻画这种运动规律,存在模式误差(孙健等,2021),直接输出预报产品的时空分辨率不能满足当前业务需求,需要进一步对模式输出产品进行后处理。常见的模式后处理方法包括模式输出统计(Glahn and Lowry, 1972)、准对称混合滑动训练期方法(吴启树等,2016)、最优集合预报订正方法(郝翠等,2019)以及卡尔曼滤波自适应误差订正方法(王丹等,2019)等,这类传统客观预报技术主要应用于站点建模,大多基于预报因子与预报量之间线性关系建立模型,无法有效处理海量气象数据信息,随着预报时空分辨率的提高和预报时效的延长,预报效果并不理想(陈昱文等,2020)。
机器学习方法也可用于天气预报中(杨璐等,2021;Han et al, 2021;张延彪等,2022a;徐景峰等,2023;陈锦鹏等,2024)。早在2009年,Paras et al(2009)引入了基于特征的神经网络模型来预报最高、最低温度,神经网络特征在不同时间段从时间序列天气参数中提取,利用前馈人工神经网络和反向传播的方式进行监督学习,展示出神经网络的巨大潜力。近年来,随着气象数据和计算资源的发展,机器学习技术在模式订正中得到广泛应用(Zhao et al, 2023;Wang et al, 2023;方鸿斌等,2024)。Cho et al(2020)应用随机森林、支持向量回归、全连接神经网络(FCNN)和多模型集成策略,建立预报量和预报因子之间的统计关系模型,以校正数值模式在城市地区极端高温的预报偏差,表明机器学习技术对于天气过程的非线性建模有显著优势。Qin et al(2023)提出了一种网格到多点(G2N)模型输出误差校正方案,通过构建AlexNet的网络架构提取空间特征并同时校正多站预测,G2N使数值模型的2 m温度预报均方根误差降低了19%。
在气象预报模型构建中,普通人工神经网络通常假定气象要素之间相互独立,并未考虑要素之间的时序关系(门晓磊等, 2019;陈鹤等,2022)。循环神经网络诸如长短期记忆网络(LSTM)等用于处理序列数据,可提取时序特征(Cho et al, 2022)。Hewage et al(2021)基于LSTM和时间卷积网络的时序建模方法,预报未来12 h的10个地面气象要素,预报效果优于WRF模式。Zhang et al(2022)应用长短期记忆-全连接网络(LSTM-FCNN)对CMA-MESO(原GRAPES-3 km)模式输出的2 m温度进行偏差订正,通过融合LSTM和FCNN,将从站点气象要素预报中挖掘的时间序列信息以及站点的海拔、经纬度信息相结合,与模式结果相比,陕西区域的站点气温预报均方根误差降低了32%。
上述研究工作主要以观测站点为预报对象,精细化格点预报的应用研究并不多。张延彪等(2022b)使用睿思高分辨率系统输出的2 m温度、2 m相对湿度、10 m纬向风风速以及10 m经向风风速格点预报数据,建立卷积神经网络模型进行偏差订正,取得一定的改善效果。然而卷积神经网络忽略了数据的时序关系,尤其对于气温这类连续性变量而言,考虑时序关系建模尤为重要,LSTM可发挥重要作用(Yan et al, 2021;张桃等,2024)。基于LSTM的建模方式是将所有站点样本进行堆叠,建立统一的预报模型,克服了传统方法中仅针对单一站点建模的局限性,可以推广至格点建模中。但是LSTM仅专注数据时序性,并未考虑其空间性(Jeong et al, 2021)。为了更好地应用空间信息,赵琳娜等(2022)曾在FCNN中融入嵌入层(ED)结构以结合站点和月份信息,核心思想是将站点号、月份特征视作分类变量而非连续变量。嵌入层最初应用于深度学习自然语言处理的词嵌入任务中,主要目的是将高维度的离散输入数据映射到低维度的连续向量空间中,可以用以处理高维分类变量(Dahouda and Joe, 2021)。
针对当前我国气象部门智能网格预报发展要求,本研究结合欧洲中期天气预报中心高分辨率模式(ECMWF-IFS)预报产品和中国气象局陆面数据同化系统(CLDAS)气温资料,构建融合LSTM、FCNN以及ED这几类不同网络结构的混合神经网络预报模型,以提高格点气温预报的时空分辨率。进一步检验评估该模型输出的湖南地区范围内逐小时格点气温预报产品、中央气象台指导预报(SCMOC) 以及逐3 h的ECMWF-IFS预报产品,验证该方法在业务上的实际应用效果,以期为精细化气温预报研究提供参考。
1 数据及预处理 1.1 资料本文采用的预报数据为ECMWF-IFS高分辨率预报产品,起报时间分别为08时(北京时,下同)和20时,预报时效15~36 h,时间分辨率3 h,地面、高空变量预报场水平分辨率分别为0.125°×0.125°和0.25°×0.25°。在业务运行中,ECMWF-IFS预报产品接收时间相比实际起报时间延迟约7 h,因此对ECMWF-IFS后处理时需采用预报时效12 h之后的预报产品。观测数据为CLDAS逐1 h气温产品,水平分辨率为0.05°×0.05°,参与对比检验的格点包括湖南省界线以内所有格点,空间范围大致为24.50°~30.25°N、108.65°~114.40°E。
预报与观测数据总时长为2017年10月至2022年12月,划分2017年10月至2021年9月为训练集,2021年10月至2021年12月为验证集,2022年为测试集。
1.2 数据预处理为获取未来24 h逐1 h气温预报结果,基于ECMWF-IFS不同起报时次,不同预报时效(15~36 h,逐3 h)单独建模,共建立16个模型。分别构建输入模型的数据集,其中特征数据集为单个预报时效的ECMWF-IFS数据,目标数据集为该预报时效对应预报时间及前2 h的观测数据,采用最近邻插值方法将ECMWF-IFS数据上采样至观测数据格点。为保证模型在训练过程尽可能收敛,在数据预处理中进行归一化处理,公式如下:
| $ X^*=\frac{X-X_{\min }}{X_{\max }-X_{\min }} $ | (1) |
式中:X*为归一化处理的数据,X为原始数据,Xmin和Xmax分别为样本数据的最小值和最大值。
为提高建模效率,增强模型泛化能力,采用相关分析法从ECMWF-IFS所有预报因子中筛选出相关变量,选择与气温实况相关系数大于0.3,且概率小于0.05的预报因子(Zhang et al, 2020)。通过计算不同预报时效ECMWF-IFS预报因子与气温实况的相关性发现,在不同预报时效中相关系数均超过0.8的因子包括2 m温度、地表温度、2 m露点温度、850/1000 hPa温度和1000 hPa比湿等。可见低空至近地面温度相关预报因子对气温预报影响较大,此外,中、低层的比湿、风场也对气温有一定贡献。除模式预报因子外,融合多源数据可以帮助建模(周康辉等,2021)。赵琳娜等(2022)指出在预报数据中融合历史观测数据(时间滞后观测变量)作为模型输入能增加神经网络学习的信息量,提高气温预报准确率。本文增加三种类型的辅助变量(时间滞后观测变量、月份和格点号),为模型提供临近气温观测信息以及时间、空间信息。当基于预报时效15~30 h(逐3 h)ECMWF-IFS数据建模时,时间滞后观测变量包括滞后1 d、滞后2 d气温观测。当基于预报时效33 h、36 h的模式预报建模时,考虑实际业务运行时,模式到报时间较晚,时间滞后观测变量只包含了滞后2 d气温观测。表 1给出最终输入各模型的共同特征。
|
|
表 1 输入模型的共同特征 Table 1 Common features of input models |
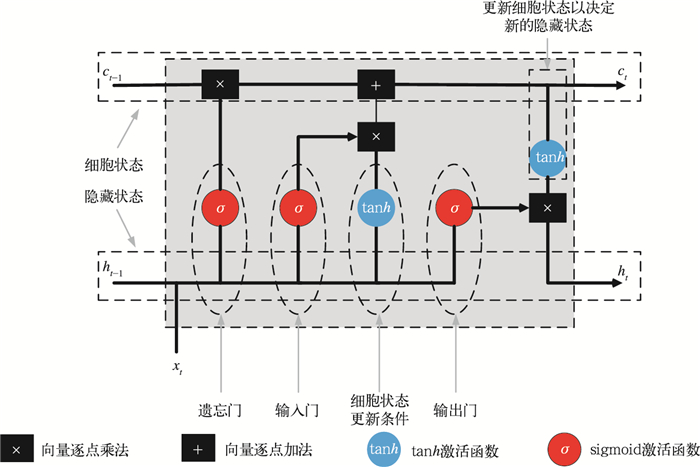
考虑到气象数据的时间关联性以及气温序列变化所具有的趋势性、周期性和连续性等特点,引入LSTM以学习ECMWF-IFS预报因子以及时间滞后观测变量(时序特征)在给定时序上的演变规律。其中,LSTM属于循环神经网络中的一种,被广泛应用至时序预测问题。与FCNN不同,LSTM有着重复的神经网络模块形成链式结构,可捕捉信息间的长距离依赖关系,同时引入特殊的门控机制,从而解决了普通循环神经网络存在的梯度爆炸和梯度弥散问题,其内部结构如图 1所示,前一个时间步的隐藏状态ht-1和当前时间步的输入xt在通过各个门之前首先合并处理,遗忘门控制忘记信息量,输入门有助于识别需要添加到细胞状态ct的重要元素,信息经历LSTM循环单元后最终更新细胞状态ct和隐藏状态ht。关于LSTM的详细运算过程可参见Hochreiter and Schmidhuber(1997)。
|
图 1 长短期记忆网络神经元结构 Fig. 1 Neuron structure of LSTM networks |
为满足LSTM输入,应用滑动时间窗口构建时序数据集。滑动时间窗口时序长度过长会导致内存消耗增加等问题,另外,为更好地帮助模型捕捉数据中周尺度趋势及变化,进一步提升平稳天气气温预报能力,本文选取时间窗口长度为7 d。在不同格点上,应用滑动时间窗口沿着时间维度进行逐日滑动。对于时序特征,形成长度为7 d的时序数据,对于目标,仅取滑动时间窗口的最后1 d,以构造多步长到单步长的时序预测任务。拼接不同格点的样本,以进一步增加样本量,保证深度学习模型训练数据量。
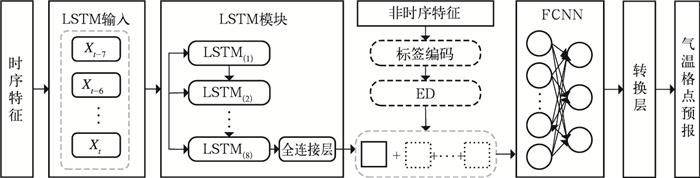
然而,有些非时序特征(格点号和月份)对于模型可能有重要影响,将此类特征连同时序特征共同输入LSTM实际上没有意义,并且降低模型训练速率。ED模块可以帮助处理此类高维分类变量,使模型能够从大量样本中识别不同月份、不同格点的样本。赵琳娜等(2022)在构建全国站点的日最高气温预报模型时发现,加入嵌入层的FCNN(简称ED-FCNN)相比普通的FCNN能取得更优的预报性能,验证了嵌入层的可用性。因此本文基于ED-FCNN模型架构,进一步引入了LSTM模块,构造多输入混合神经网络ED-LSTM-FCNN模型(图 2),以接收不同类型数据。时序特征输入LSTM模块进行特征提取,非时序特征输入ED层进行数据分类、降维处理,由FCNN接收LSTM与ED模块的输出,对提取的高阶特征进行解码,最后由转换层将拼接数据重组为格点数据输出。
|
图 2 ED-LSTM-FCNN模型结构 Fig. 2 Structure of ED-LSTM-FCNN model |
本文模型超参数设置见表 2。为帮助模型在训练中更好地拟合数据,增强模型泛化能力,采用早停法进行训练,当模型在验证集上连续3个时期损失值不降反增时,停止训练,并保存在训练过程中验证集上表现最优的模型。
|
|
表 2 模型训练超参数设置 Table 2 Hyperparameter settings in model training |
为评估模型在测试集上的表现效果,采用的检验方法包括均方根误差(RMSE)、平均偏差(ME)与气温预报准确率(F2):
| $ \mathrm{RMSE}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(O_i-P_i\right)^2} $ | (2) |
| $ \mathrm{ME}=\frac{1}{n} \sum\limits_{i=1}^n\left(P_i-O_i\right) $ | (3) |
| $ F_2=\frac{n_2}{n} \times 100 \% $ | (4) |
式中:Oi和Pi分别代表第i个样本的观测值与预报值,n2为气温预报值与观测值绝对误差不超过2℃的样本量,n为总样本量。
3 结果分析 3.1 分时效预报效果检验为验证LSTM模块的有效性,基于ED-LSTM-FCNN模型进行消融试验,去除模型中LSTM模块,直接将时序特征与经过嵌入层处理后的非时序特征拼接后输入FCNN。省级预报业务中常用SCMOC作为参考预报源,因此分别对比ED-LSTM-FCNN、ED-FCNN、ECMWF-IFS和SCMOC预报效果。本文图中结果统一使用实际业务起报时间(数值模式起报时间+12 h、预报时效-12 h)。当ECMWF-IFS预报产品的起报时次为08时、20时,预报时效为12~36 h,对应SCMOC和深度学习模型产品的起报时次为20时、08时,预报时效为0~24 h。
图 3为不同起报时次、不同预报时效的深度学习模型、ECMWF-IFS和SCMOC的RMSE对比。从逐3 h预报来看,ECMWF-IFS模式08时、20时(对应实际业务20时、08时,即分别对应图 3a, 3b)起报的RMSE分别介于1.8~2.6℃和1.8~2.4℃,在不同起报时次的预报误差日变化特征相似,午后预报误差较大,凌晨较小。模式不同起报时次对高、低温时段的预报效果各有优劣,08时起报(截取预报时段为当日20时至次日20时)与20时相比,低温时段更接近于起报时次,因此对于低温时段的预报误差要更小(图 3a);当起报时次为20时(截取预报时段为次日08时至第三日08时),对于白天的高温预报效果更优(图 3b)。综合两个起报时次的检验结果可见,ED-LSTM-FCNN、ED-FCNN模型有效降低了ECMWF-IFS的RMSE,降幅分别达25.4%~37.7%和20.2%~29.6%,误差日变化趋势与模式相似,说明深度学习模型的预报效果与模式产品相关性较大。对比逐1 h深度学习模型与SCMOC产品预报效果,ED-LSTM-FCNN、ED-FCNN模型的RMSE分别介于1.2~2.0℃、1.3~2.1℃,与SCMOC相比分别降低了15.8%~40.0%和6.2%~33.5%。ED-LSTM-FCNN模型在不同起报时次、所有预报时效上RMSE均最低,20时、08时起报的RMSE与ED-FCNN模型相比分别降低了3.5%~19.3%和5.9%~16.6%,可见LSTM模块的引入对于模型性能提升至关重要,由于不同类型的气象现象具有不同时间尺度特征,LSTM的记忆单元能够有效学习序列中的长期依赖关系,帮助模型更好地理解气象数据的变化趋势。经过LSTM提取的时序特征输送至FCNN,再由FCNN整合该时序特征以及嵌入层输出的非时序特征,融入空间和月份信息,增强模型对复杂数据样本的辨识及拟合能力,进一步提升了ED-LSTM-FCNN模型的预测准确性。

|
图 3 2022年湖南不同预报产品(a)20时、(b)08时起报的各预报时效气温预报均方根误差 注:柱状上方标注表示ECMWF-IFS在15~36 h(逐3 h)预报时效的气温预报均方根误差。 Fig. 3 RMSE of different temperature forecast products with different lead times initiated in Hunan Province at (a) 20:00 BT and (b) 08:00 BT in 2022 |
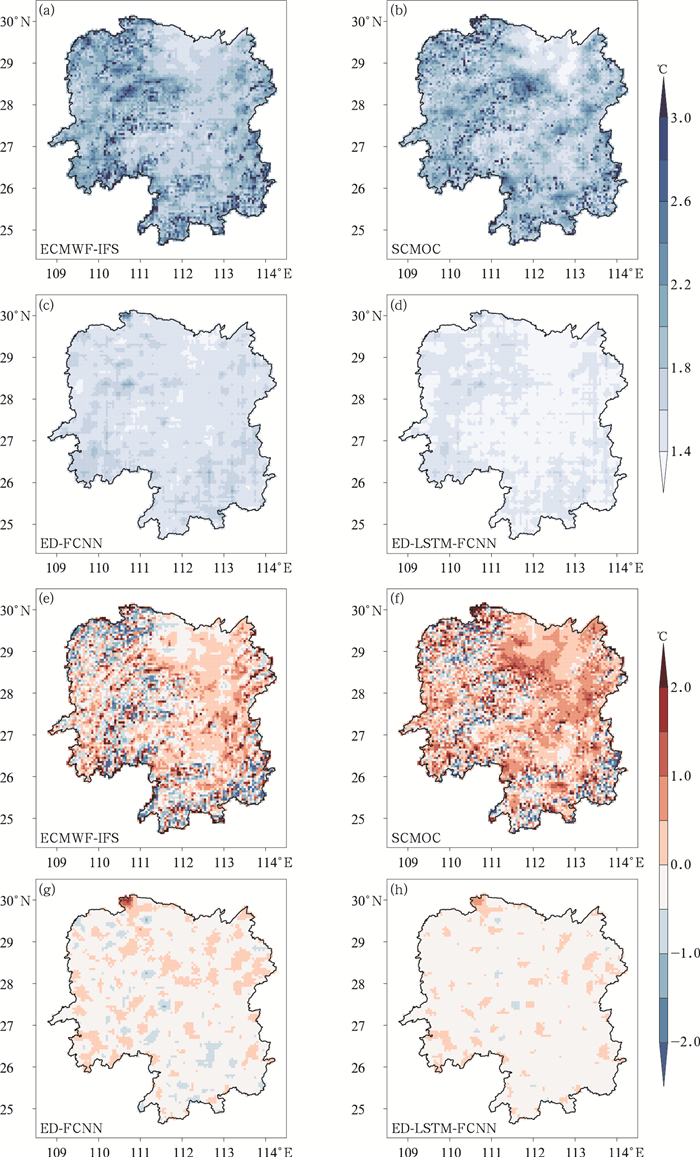
图 4为湖南地区2022年ECMWF-IFS逐3 h、SCMOC、深度学习模型逐1 h气温预报的平均RMSE(图 4a~4d)与ME(图 4e~4h)空间分布。ECMWF-IFS的RMSE空间分布特征与湖南地形结构相似,湖南西北、西南、南部以及东部分别分布有武陵山脉、雪峰山脉、南岭以及罗霄山脉,该区域RMSE达2.0℃以上,最高值为6.5℃,中部丘陵盆地地势相对低平,RMSE为1.6~2.0℃,北部洞庭湖平原为1.4~1.6℃。SCMOC的RMSE空间分布也呈现明显的地形相关特征,介于1.3~6.6℃,与ECMWF-IFS相比对于北部平原预报效果更好。ED-LSTM-FCNN和ED-FCNN模型有效降低了ECMWF-IFS的系统性偏差,整体预报效果优于SCMOC,RMSE分别介于1.2~2.0℃和1.3~2.7℃,显著降低了西部、南部和东部复杂地形区域的预报误差。统计上述预报产品在不同RMSE区间上的格点数占总格点数的比例,以1.2~1.4℃为例,ED-LSTM-FCNN、ED-FCNN、SCMOC和ECMWF-IFS的比例分别约为52.7%、4.0%、2.2%和0.0%,即ED-LSTM-FCNN模型超过一半区域RMSE低于1.4℃,且主要分布在向北开口的马蹄形盆地区,而ED-FCNN模型占比仅为4.0%,可见ED-LSTM-FCNN模型在空间上应用效果优于ED-FCNN模型。
|
图 4 2022年湖南不同预报产品气温预报的平均(a, b, c, d)RMSE和(e, f, g, h)ME空间分布 Fig. 4 Spatial distribution of average (a, b, c, d) RMSE and (e, f, g, h) ME of different temperature forecast products in Hunan Province in 2022 |
RMSE可反映整体偏差幅度,但忽略误差正负向问题,为了考量不同预报产品定量订正效果,进一步评估ME的空间分布。ECMWF-IFS和SCMOC在中部、北部的丘陵盆地和平原区预报比实况整体偏高,在山原山地区预报比实况整体偏低,ME分别介于-4.3~6.2℃和-4.8~6.4℃。对比来看,两种深度学习模型明显降低了湖南全区域的ME绝对值,其中ED-LSTM-FCNN模型将ME绝对值降低至1.0℃以内,绝大部分地区介于-0.5~0℃,优于ED-FCNN模型。
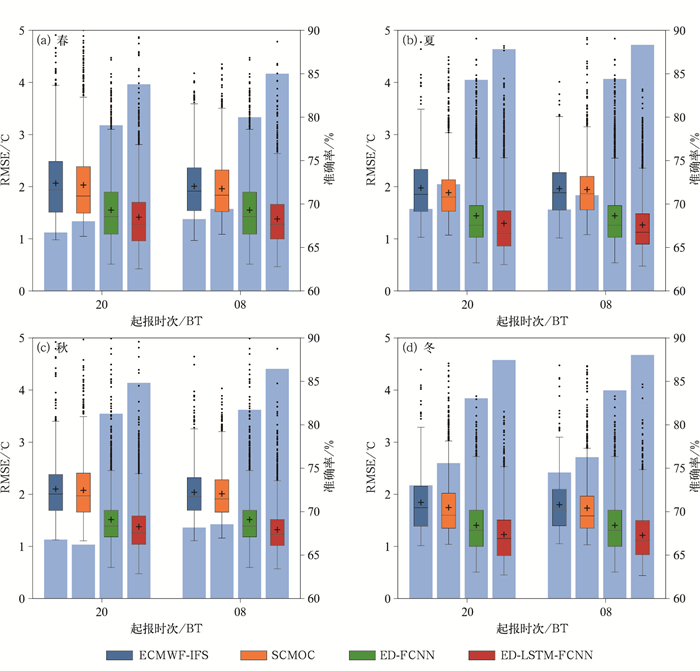
从不同季节气温预报RMSE箱线图(图 5)来看,无论是20时还是08时起报,深度学习模型RMSE分布的均值和中位数明显低于ECMWF-IFS与SCMOC。而在箱体两端出现误差较大的离群点,说明经过模型订正后仍然会出现个别天数预报误差与实况有较大差距的情况。以20时起报为例,四种产品在冬季预报效果均优于其他季节,RMSE的均值和中位数分别为1.8℃和1.7℃(ECMWF-IFS)、1.7℃和1.6℃(SCMOC)、1.2℃和1.2℃(ED-LSTM-FCNN)、1.4℃和1.3℃(ED- FCNN)。在不同季节,ED-LSTM-FCNN模型RMSE分布的均值和中位数均为最低,例如,与春季均值相比,相对于ECMWF-IFS、SCMOC和ED-FCNN模型分别下降了33.3%、30.0%和12.5%。同时从气温预报准确率(图 5)可见,ED-LSTM-FCNN模型最高,在不同季节均可达到83.0%以上,夏季达到88.3%。
|
图 5 2022年湖南不同预报产品在不同起报时次、不同季节气温预报的RMSE(箱线图)与平均准确率(柱状) 注:箱线图箱体中横线为中位数,“+”为均值,箱体上端及下端分别为第75%和25%分位值,触须的上端和下端分别代表除异常值外的最大值和最小值,尾端实心点为超出第75%分位值差3倍距离的异常值。 Fig. 5 RMSE (box plot) and average accuracy (bar) of different temperature forecast products initiated at different times in Hunan Province in different seasons of 2022 |
温度过高或过低导致的高低温事件(如寒潮和高温热浪)更易对公众和农牧业生产等活动产生重要影响,因此,本文评估了在超阈值样本上不同预报产品的预报效果。超阈值分为超高温阈值和超低温阈值(邱贵强等,2023),高低温阈值分别通过实况数据的第90%、10%分位值确定,分别计算湖南境内各格点的高低温阈值,基于选出的超阈值样本分别计算RMSE、ME和F2(表 3)。08时起报的深度学习模型对于极端高温的预报效果优于20时起报,与3.1节中结论一致。ED-LSTM-FCNN模型在不同起报时次对于各格点上相对极端的气温预报效果最优。针对超高温阈值,08时、20时起报的ED-LSTM-FCNN模型RMSE分别为约1.4℃和1.6℃,相比ECMWF-IFS(SCMOC)分别降低了41.7%和36.0%(30.0%和27.3%),预报准确率分别提高了47.6%和46.6%(22.5%和28.0%);超低温阈值预报的RMSE分别为1.3℃和1.2℃,相比ECMWF-IFS(SCMOC)分别降低了27.8%和33.3%(27.8%和33.3%),预报准确率分别提高了14.0%和15.1%(16.1%和18.1%),且明显优于ED-FCNN模型。从ME来看,不同预报产品对于超低(高)温阈值样本预报均偏高(低)。
|
|
表 3 2022年湖南不同预报产品对超阈值气温预报的RMSE、ME与F2 Table 3 RMSE, ME and F2 of different forecast products for temperature above thresholds in Hunan Province in 2022 |
为具体评估各预报产品在极端天气情况下的预报能力,本文选取2022年8月17—19日的极端高温过程和2022年11月27—29日的强降温过程分别进行评估。
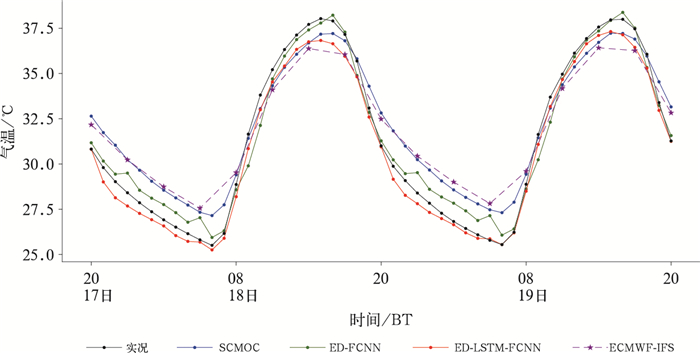
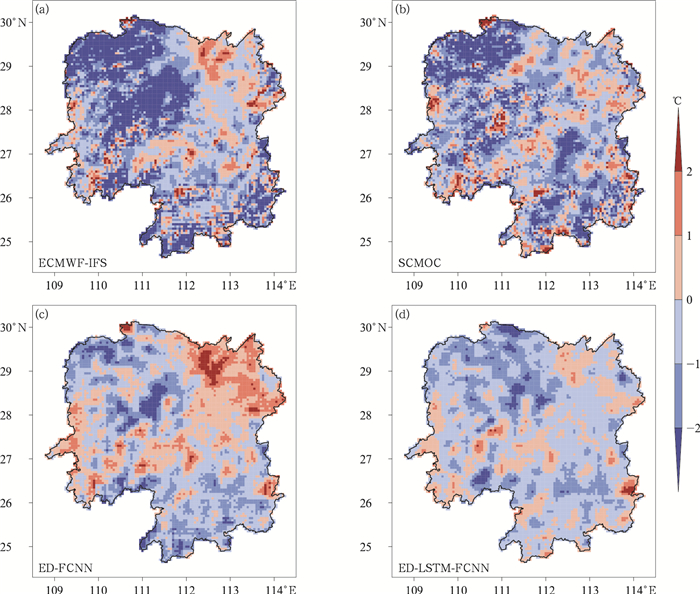
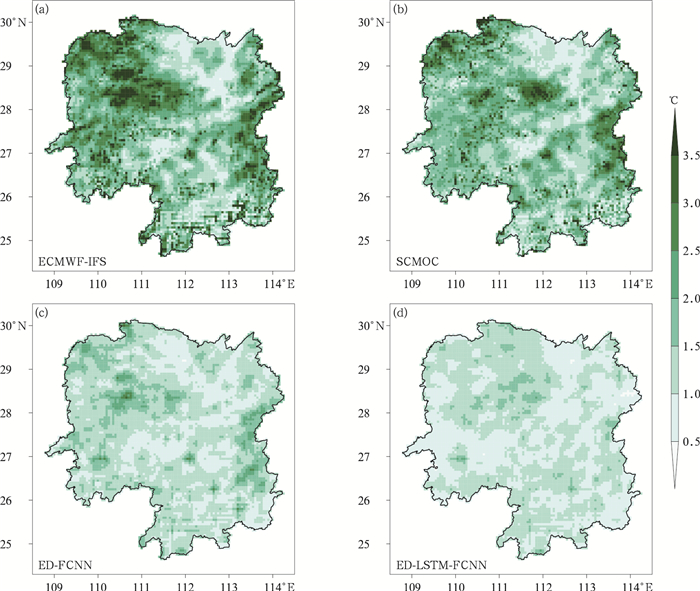
从高温个例来看,湖南地区大部分时段受500 hPa西太平洋副热带高压控制,维持晴热少雨天气。模式在夜间对于平均气温预报明显偏高(图 6),大部分区域气温预报值高于观测值,偏差在2.0℃以上(图略)。在ED-LSTM-FCNN模型中,加入了时间滞后观测变量,对于这种平稳性的天气过程,观测数据能够提供对模式的约束,此外LSTM模块擅长捕捉时序演变特征,进一步修正模式偏差,在夜间预报效果优于其他产品。而对于一天中的高温时段,模式预报比实况明显偏低,尤其在武陵山和雪峰山等高海拔地区。图 7为8月19日14时气温预报值与观测值的偏差空间分布,ED-LSTM-FCNN模型在绝大部分地区预报比实况略偏低,RMSE为0.9℃,ED-FCNN模型则在部分地区(如洞庭湖平原区)预报比实况明显偏高,RMSE为1.1℃。在模型训练中,训练数据未包含足够的高温天气样本,模型无法充分学习高温天气的特征,导致极端高温预报略有偏差。从整个高温过程的RMSE空间分布来看(图 8),ECMWF-IFS在湖南西北部、东部武功山、连云山等山丘地区误差达2.5℃以上,而深度学习模型尤其ED-LSTM-FCNN模型在湖南绝大部分区域误差低于1.5℃,预报效果明显优于其他产品。
|
图 6 2022年8月17日20时至19日20时湖南不同预报产品平均气温预报与实况对比 Fig. 6 Comparison between the average temperature forecast of different forecast products and observations in Hunan Province from 20:00 BT 17 to 20:00 BT 19 August 2022 |
|
图 7 2022年8月19日14时湖南不同预报产品气温预报值与观测值的偏差空间分布 Fig. 7 Spatial distribution of the deviation between different temperature forecast products and observations in Hunan Province at 14:00 BT 19 August 2022 |
|
图 8 2022年8月17—19日湖南不同预报产品气温预报的RMSE空间分布 Fig. 8 Spatial distribution of RMSE in different temperature forecast products in Hunan Province from 17 to 19 August 2022 |
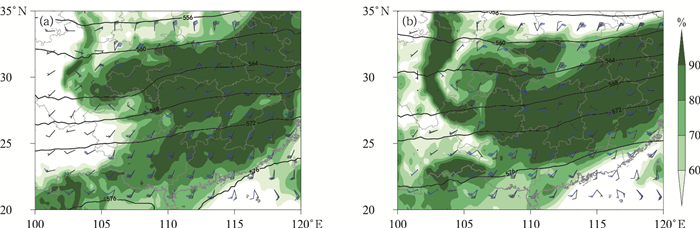
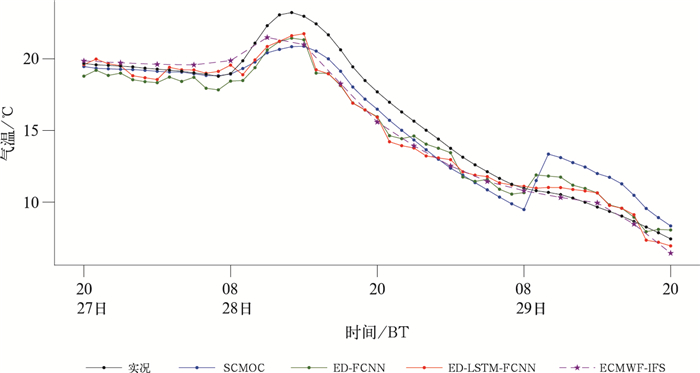
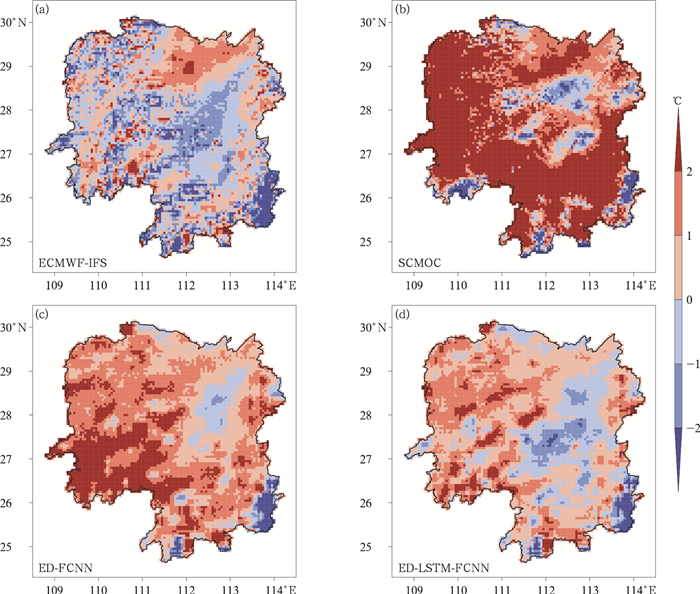
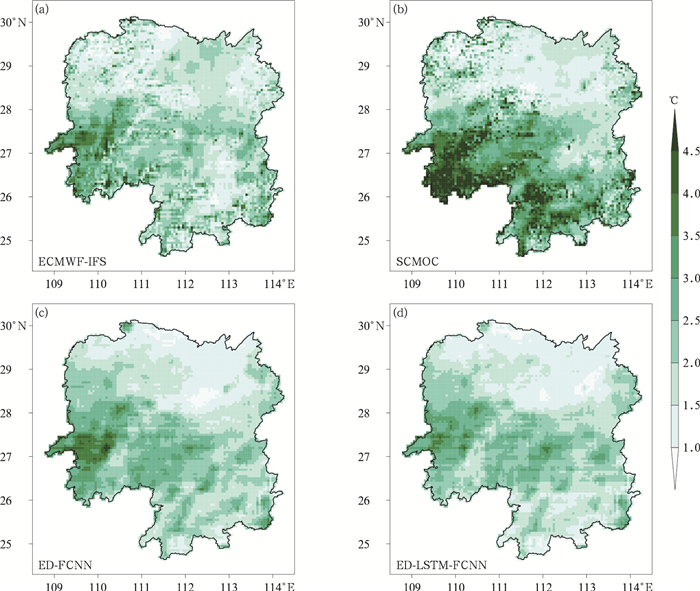
2022年11月27—29日的过程是一次寒潮降温伴随较强降水天气过程(图 9)。11月27日开始,湖南地区850 hPa中低空为较强西南气流,切变线位于湖南北部地区,相对湿度在90%以上,动力和水汽条件充沛,有利于降水发生,同时近地面有冷空气渗透南下。28日14时,切变线开始缓慢南移,925 hPa高度以下中部以北地区已转成偏北风,风速达10 m·s-1,至次日02时,850 hPa切变线已南移至湘南地区,925 hPa全省转为偏北风,最大风速达20 m·s-1以上,在此期间配合较好的水汽、动力条件,全省出现小到中雨。受强冷空气与降水的共同影响,全省平均气温从28日14时至29日20时持续下降(图 10),达到寒潮标准,而SCMOC和ED-FCNN模型预报29日上午平均气温为上升趋势。图 11为11月29日11时气温预报与观测的偏差空间分布,ED-LSTM-FCNN模型在湘西、湘南等地预报高于实况,ED-FCNN模型和SCMOC偏高的范围和程度更明显,前一天同时段气温呈增加趋势,模型预报结果可能受到前期气温趋势影响。从整个强降温过程的RMSE空间分布来看(图 12),ECMWF-IFS在湘西南地区(山地为主)误差达3.0℃以上,高于其他区域。SCMOC在雪峰山、南岭等地气温预报误差甚至达到4.0℃以上。深度学习模型对于湘北地区模式预报误差有一定订正效果,其他地区效果不佳。从过程的逐3 h偏差空间分布来看(图略),ED-LSTM-FCNN模型无法显著改善模式预报,RMSE由2.4℃降低至2.1℃,但仍然优于SCMOC,逐1 h气温预报的RMSE相比SCMOC降低了14.8%。综上,ED-LSTM-FCNN模型对于大范围复杂的强降温过程预报能力稍弱,可能原因在于训练数据集中强降温过程的样本占比较少,影响此类天气形势下的模型预报能力。
|
图 9 2022年11月(a)28日14时, (b)29日02时500 hPa高度场(等值线,单位:dagpm)、850 hPa风场(蓝色风羽)、850 hPa相对湿度(填色)和925 hPa风场(黑色风羽) Fig. 9 500 hPa height (contour, unit: dagpm), 850 hPa wind (blue barb), 850 hPa relative humidity (colored) and 925 hPa wind (black barb) at (a) 14:00 BT 28 and (b) 02:00 BT 29 November 2022 |
|
图 10 2022年11月27日20时至29日20时湖南不同预报产品平均气温预报与实况对比 Fig. 10 Comparison between the average temperature forecast of different forecast products and observations in Hunan Province from 20:00 BT 27 to 20:00 BT 29 November 2022 |
|
图 11 2022年11月29日11时湖南不同预报产品气温预报值与观测值偏差的空间分布 Fig. 11 Spatial distribution of the deviation between different temperature forecast products and observations in Hunan Province at 11:00 BT 29 November 2022 |
|
图 12 2022年11月27—29日湖南不同预报产品气温预报的RMSE空间分布 Fig. 12 Spatial distribution of RMSE in different temperature forecast products in Hunan Province from 27 to 29 November 2022 |
本文利用ECMWF-IFS高分辨率预报产品和中国气象局逐1 h气温实况资料建立了ED-LSTM-FCNN模型,实现湖南地区逐1 h精细化格点气温预报。为验证模型中LSTM模块有效性,进行消融实验构建ED-FCNN模型。综合检验评估ECMWF- IFS、SCMOC、ED-LSTM-FCNN和ED-FCNN模型预报效果,主要结论如下:
(1) 深度学习模型对于逐3 h气温预报RMSE显著低于ECMWF-IFS,降幅为20.2%~37.7%,逐1 h气温预报RMSE显著低于SCMOC,降幅为6.2%~40.0%。其中,ED-LSTM-FCNN模型在不同起报时次、所有预报时效上RMSE均最低,与ED-FCNN模型相比降低了3.5%~19.3%。
(2) 从空间分布来看,深度学习模型均能有效降低ECMWF-IFS的系统性偏差,且整体预报效果优于SCMOC,尤其在湖南西部、南部和东部的复杂地形区域。ED-LSTM-FCNN模型在湖南中部丘陵盆地和北部平原地区RMSE为1.4℃以下,格点数占总格点数的比例为52.7%,远高于ECMWF-IFS(0.0%)、SCMOC(2.2%)和ED-FCNN模型(4.0%)。从季节尺度上来看,ED-LSTM-FCNN模型在各个季节误差分布的均值与ECMWF-IFS、SCMOC、ED-FCNN模型相比降幅分别为33.3%~35.0%、29.4%~33.3%和6.7%~14.3%。
(3) ED-LSTM-FCNN模型在不同起报时次对于相对极端的气温值预报效果最优,在20时起报对于超低(高)温阈值预报的RMSE与ECMWF-IFS、SCMOC、ED-FCNN模型相比分别降低了30.3%、33.0%和8.3%(35.9%、26.7%和7.6%);08时起报分别降低了29.0%、31.7%和7.4%(41.8%、29.6%和12.7%)。通过个例分析对比可知,ED-LSTM-FCNN模型对于相对平稳、连续性天气的气温预报效果很好,对于较复杂的强降温过程(转折性天气)预报效果稍有欠缺,可能与数据集中转折性天气样本占比较少有关。
(4) ED-LSTM-FCNN模型相对于ED-FCNN模型能够更好地从短期历史气象要素时间序列中提取到深层特征信息,从而改善预报效果,并且模型属于轻量级深度学习模型,具有计算资源需求低、推断速度快、便于迭代和试验等优势。消融试验表明,LSTM模块加入尤为重要,LSTM的门控机制允许模型在不同时间尺度上适应数据模式,可以同时捕获短期和长期特征。但ED-LSTM-FCNN模型对于转折性天气的气温预报改善效果不明显,后期可以引入注意力机制或者卷积层模块来捕获气象数据中局部时间和空间模式,也可以针对转折性天气样本单独建模,以进一步提升复杂天气形势下的气温预报水平。
陈鹤, 蔡荣辉, 陈静静, 等, 2022. 基于深度学习方法的气温预报技术应用与评估[J]. 气象, 48(11): 1373-1383. Chen H, Cai R H, Chen J J, et al, 2022. Application and evaluation of temperature forecast based on deep learning method[J]. Meteor Mon, 48(11): 1373-1383 (in Chinese). DOI:10.7519/j.issn.1000-0526.2022.070101
|
陈锦鹏, 黄奕丹, 朱婧, 等, 2024. 集成学习和动态融合算法在福建省短时强降水预报中的应用[J]. 气象, 50(1): 48-58. Chen J P, Huang Y D, Zhu J, et al, 2024. Application of ensemble learning and dynamic fusion for short-time severe rainfall forecasting in Fujian Province[J]. Meteor Mon, 50(1): 48-58 (in Chinese).
|
陈昱文, 黄小猛, 李熠, 等, 2020. 基于ECMWF产品的站点气温预报集成学习误差订正[J]. 应用气象学报, 31(4): 494-503. Chen Y W, Huang X M, Li Y, et al, 2020. Ensemble learning for bias correction of station temperature forecast based on ECMWF products[J]. J Appl Meteor Sci, 31(4): 494-503 (in Chinese).
|
方鸿斌, 王珊珊, 王晓玲, 等, 2024. 基于机器学习的格点气温预报订正方法[J]. 气象, 50(1): 103-114. Fang H B, Wang S S, Wang X L, et al, 2024. Gridded temperature forecast correction method based on machine learning[J]. Meteor Mon, 50(1): 103-114 (in Chinese).
|
郝翠, 张迎新, 王在文, 等, 2019. 最优集合预报订正方法在客观温度预报中的应用[J]. 气象, 45(8): 1085-1092. Hao C, Zhang Y X, Wang Z W, et al, 2019. Application of analog ensemble rectifying method in objective temperature prediction[J]. Meteor Mon, 45(8): 1085-1092 (in Chinese).
|
刘新伟, 段伯隆, 黄武斌, 等, 2020. 基于小波分析的客观预报方法在智能网格高低温预报中的应用[J]. 大气科学学报, 43(3): 577-584. Liu X W, Duan B L, Huang W B, et al, 2020. Application of objective prediction method based on wavelet analysis in intelligent grid high and low temperature prediction[J]. Trans Atmos Sci, 43(3): 577-584 (in Chinese).
|
门晓磊, 焦瑞莉, 王鼎, 等, 2019. 基于机器学习的华北气温多模式集合预报的订正方法[J]. 气候与环境研究, 24(1): 116-124. Men X L, Jiao R L, Wang D, et al, 2019. A temperature correction method for multi-model ensemble forecast in North China based on machine learning[J]. Climatic Environ Res, 24(1): 116-124 (in Chinese).
|
邱贵强, 时少英, 王洪霞, 等, 2023. 2 m气温集成订正方法及在冬奥延庆赛区的应用[J]. 应用气象学报, 34(4): 400-412. Qiu G Q, Shi S Y, Wang H X, et al, 2023. An integrated correction method for 2 m temperature and its application to Yanqing Competition Zone of Olympic Winter Games[J]. J Appl Meteor Sci, 34(4): 400-412 (in Chinese).
|
孙健, 曹卓, 李恒, 等, 2021. 人工智能技术在数值天气预报中的应用[J]. 应用气象学报, 32(1): 1-11. Sun J, Cao Z, Li H, et al, 2021. Application of artificial intelligence technology to numerical weather prediction[J]. J Appl Meteor Sci, 32(1): 1-11 (in Chinese).
|
王丹, 王建鹏, 白庆梅, 等, 2019. 递减平均法与一元线性回归法对ECMWF温度预报订正能力对比[J]. 气象, 45(9): 1310-1321. Wang D, Wang J P, Bai Q M, et al, 2019. Comparative correction of air temperature forecast from ECMWF model by the decaying averaging and the simple linear regression methods[J]. Meteor Mon, 45(9): 1310-1321 (in Chinese).
|
吴启树, 韩美, 郭弘, 等, 2016. MOS温度预报中最优训练期方案[J]. 应用气象学报, 27(4): 426-434. Wu Q S, Han M, Guo H, et al, 2016. The optimal training period scheme of MOS temperature forecast[J]. J Appl Meteor Sci, 27(4): 426-434 (in Chinese).
|
徐景峰, 宋林烨, 陈明轩, 等, 2023. 冬奥会复杂山地百米尺度10 m风速预报的机器学习订正对比试验[J]. 大气科学, 47(3): 805-824. Xu J F, Song L Y, Chen M X, et al, 2023. Comparative machine learning-based correction experiment for a 10 m wind speed forecast at a 100 m resolution in complex mountainous areas of the Winter Olympic Games[J]. Chin J Atmos Sci, 47(3): 805-824 (in Chinese).
|
杨璐, 南刚强, 陈明轩, 等, 2021. 基于三种机器学习方法的降水相态高分辨率格点预报模型的构建及对比分析[J]. 气象学报, 79(6): 1022-1034. Yang L, Nan G Q, Chen M X, et al, 2021. The construction and comparison of high resolution precipitation type prediction models based on three machine learning methods[J]. Acta Meteor Sin, 79(6): 1022-1034 (in Chinese).
|
张桃, 林鹏飞, 刘海龙, 等, 2024. 利用长短期记忆网络LSTM对赤道太平洋海表面温度短期预报[J]. 大气科学, 48(2): 1-10. Zhang T, Lin P F, Liu H L, et al, 2024. Short- term sea surface tempera- ture forecasts for the equatorial Pacific based on long short-term memory network[J]. Chin J Atmos Sci, 48(2): 1-10 (in Chinese).
|
张延彪, 陈明轩, 韩雷, 等, 2022a. 数值天气预报多要素深度学习融合订正方法[J]. 气象学报, 80(1): 153-167. Zhang Y B, Chen M X, Han L, et al, 2022a. Multi-element deep learning fusion correction method for numerical weather prediction[J]. Acta Meteor Sin, 80(1): 153-167 (in Chinese).
|
张延彪, 宋林烨, 陈明轩, 等, 2022b. 基于卷积神经网络的京津冀地区高分辨率格点预报偏差订正试验[J]. 大气科学学报, 45(6): 850-862. Zhang Y B, Song L Y, Chen M X, et al, 2022b. A study of error correction for high-resolution gridded forecast based on a convolutional neural network in the Beijing-Tianjin-Hebei Region[J]. Trans Atmos Sci, 45(6): 850-862 (in Chinese).
|
赵琳娜, 卢姝, 齐丹, 等, 2022. 基于全连接神经网络方法的日最高气温预报[J]. 应用气象学报, 33(3): 257-269. Zhao L N, Lu S, Qi D, et al, 2022. Daily maximum air temperature forecast based on fully connected neural network[J]. J Appl Meteor Sci, 33(3): 257-269 (in Chinese).
|
周康辉, 郑永光, 王婷波, 2021. 利用深度学习融合NWP和多源观测数据的闪电落区短时预报方法[J]. 气象学报, 79(1): 1-14. Zhou K H, Zheng Y G, Wang T B, 2021. Very short-range lightning forecasting with NWP and observation data: a deep learning approach[J]. Acta Meteor Sin, 79(1): 1-14 (in Chinese).
|
Cho D, Yoo C, Im J, et al, 2020. Comparative assessment of various machine learning-based bias correction methods for numerical weather prediction model forecasts of extreme air temperatures in urban areas[J]. Earth Space Sci, 7(4): e2019EA000740. DOI:10.1029/2019EA000740
|
Cho D, Yoo C, Son B, et al, 2022. A novel ensemble learning for post-processing of NWP model's next-day maximum air temperature forecast in summer using deep learning and statistical approaches[J]. Wea Clim Extrem, 35: 100410. DOI:10.1016/j.wace.2022.100410
|
Dahouda M K, Joe I, 2021. A deep-learned embedding technique for categorical features encoding[J]. IEEE Access, 9: 114381-114391.
|
Glahn H R, Lowry D A, 1972. The use of model output statistics (MOS) in objective weather forecasting[J]. J Appl Meteor Climatol, 11(8): 1203-1211. DOI:10.1175/1520-0450(1972)011<1203:TUOMOS>2.0.CO;2
|
Han L, Chen M X, Chen K K, et al, 2021. A deep learning method for bias correction of ECMWF 24-240 h forecasts[J]. Adv Atmos Sci, 38(9): 1444-1459. DOI:10.1007/s00376-021-0215-y
|
Hewage P, Trovati M, Pereira E, et al, 2021. Deep learning-based effective fine-grained weather forecasting model[J]. Pattern Anal Appl, 24(1): 343-366. DOI:10.1007/s10044-020-00898-1
|
Hochreiter S, Schmidhuber J, 1997. Long short-term memory[J]. Neural Comput, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735
|
Jeong S, Park I, Kim H S, et al, 2021. Temperature prediction based on bidirectional long short-term memory and convolutional neural network combining observed and numerical forecast data[J]. Sensors, 21(3): 941. DOI:10.3390/s21030941
|
Paras S M, Kumar A, Chandra M, 2009. A feature based neural network model for weather forecasting[J]. Int J Comput Intelligence, 4(3): 209-216.
|
Qin Y, Liu Y B, Jiang X Y, et al, 2023. Grid-to-point deep-learning error correction for the surface weather forecasts of a fine-scale numerical weather prediction system[J]. Atmosphere, 14(1): 145. DOI:10.3390/atmos14010145
|
Wang F, Tian D, Carroll M, 2023. Customized deep learning for precipitation bias correction and downscaling[J]. Geosci Model Dev, 16(2): 535-556. DOI:10.5194/gmd-16-535-2023action?journalTitle=自动化博览&year=2024&firstpage=44&issue=03
|
Yan R, Liao J Q, Yang J, et al, 2021. Multi-hour and multi-site air quality index forecasting in Beijing using CNN, LSTM, CNN-LSTM, and spatiotemporal clustering[J]. Expert Syst Appl, 169: 114513. DOI:10.1016/j.eswa.2020.114513
|
Zhang C J, Zeng J, Wang H Y, et al, 2020. Correction model for rainfall forecasts using the LSTM with multiple meteorological factors[J]. Meteor Appl, 27(1): e1852. DOI:10.1002/met.1852
|
Zhang H, Wang Y Q, Chen D D, et al, 2022. Temperature forecasting correction based on operational GRAPES-3km model using machine learning methods[J]. Atmosphere, 13(2): 362. DOI:10.3390/atmos13020362
|
Zhao L N, Lu S, Qi D, 2023. Improvement of maximum air temperature forecasts using a stacking ensemble technique[J]. Atmosphere, 14(3): 600. DOI:10.3390/atmos14030600
|
 2025, Vol. 51
2025, Vol. 51 
