2. 西藏自治区气象台,拉萨 850000;
3. 中国人民解放军95820部队,北京 102206;
4. 中国科学院大气物理研究所云降水物理与强风暴重点实验室,北京 100029
2. Meteorological Observatory of Tibet Autonomous Region, Lhasa 850000;
3. 95820 Troops of People's Liberation Army, Beijing 102206;
4. Key Laboratory of Cloud-Precipitation Physics and Severe Storms, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029
预报检验评估是对预报产品的质量进行估算和评价的过程,是天气预报业务发展中的重要环节(陈法敬等,2019;Jolliffe and Stephenson, 2012;Casati et al, 2008),可反映产品和系统的性能,为应用提供客观参考。强对流天气由于时空尺度小等属性导致预报难度大(Yano et al, 2015),对其预报性能的评估促进了预报检验技术进步(Ebert, 2008; Kok et al, 2008)。王新敏和栗晗(2020)采用FSS(fraction skill score)和连续雨区方法对模式台风暴雨进行了空间检验评估。国家气象中心还建立了全流程的检验评估程序,以实时评估预报的各方面性能(刘凑华等,2023)。
随着预报对象精细化程度的加深和分辨率的提升,传统点对点检验难以准确反映预报方法和产品的真实性能(Gilleland et al, 2009)。强对流天气有空间尺度小和生消发展快的特点,造成灾害的尺度范围往往较小,而空间检验方法可以更准确地反映产品的性能属性特征。当前我国强对流预报业务评估中使用点-面空间检验方法对预报效果进行评估。该方法以国家检验站作为基本参考,通过检索检验站周围40 km范围内加密自动气象观测(闪电为闪电定位仪监测)的方式,将加密自动站实况纳入了检验流程(唐文苑等,2017;田付友等,2015),既充分应用了多种实况监测资料,又可反映强对流预报更真实的能力水平,因此是我国强对流业务检验中的常用方法。
融合物理理解与模糊逻辑人工智能方法的分类强对流客观短期预报系统已经业务化运行,实时生成的客观概率预报产品已纳入国家级智能网格预报产品体系。该分类强对流客观短期预报系统以对雷暴、短时强降水(≥20 mm·h-1)、雷暴大风(≥17.2 m·s-1)和冰雹(直径≥5 mm)发生发展的大尺度环境特征和物理理解为基础(田付友等,2024),基于对四类强对流天气构成要素的不同,从物理成因角度出发,分别筛选对四类强对流天气具有表征意义的物理量,并结合模糊逻辑人工智能方法,实现了短期时效内的雷暴、短时强降水、雷暴大风和冰雹客观概率预报落区的自动化制作,但尚缺乏对四类强对流天气预报性能更为详细的了解。预报产品以概率的形式给出,在展示强对流天气预报落区的同时,也传递了关于预报不确定性的信息,因此对其确定性属性和概率性属性结果进行评估,对理解产品的性能、促进产品的深入应用,甚或明确后续重点改进方向,均有重要的意义。
1 资料和方法 1.1 资料及其处理本文涉及的资料包括雷暴、短时强降水、雷暴大风和冰雹格点概率预报资料及相应的实况观测。分类强对流格点概率预报基于NCEP-GFS(National Centers for Environmental Prediction Global Forecast System)资料制作,每天08时和20时(北京时,下同)起报,时空分辨率为3 h和0.5°,具体制作方式可见参考文献(田付友等,2024)。统计检验部分仅对2022年4月1日至9月30日期间每日08时起报96 h内的分类强对流预报结果进行检验。考虑业务预报的时效覆盖长度以12 h居多(唐文苑等,2017),为便于对比,将96 h内3 h间隔的预报资料整合为8个时次的12 h间隔预报。具体方法为:通过对比12 h内5个时次的格点概率值,采用保留最大概率值的方式得到覆盖12 h时效的预报结果。预报个例为2022年6月12日20时起报13日20时的分类强对流预报落区。
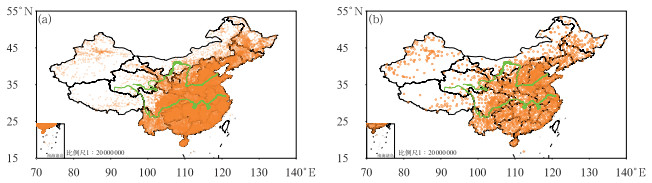
分类强对流实况为业务预报检验中使用的由闪电定位仪提供的闪电定位资料, 取自加密自动站的整点时刻短时强降水实况(图 1a), 取自加密自动站的雷暴大风实况和冰雹监测实况。其中,使用卫星监测和雷达回波等资料对短时强降水、雷暴大风和冰雹进行了基本的质量控制(郑永光等,2013),但由于2014年起冰雹仅在白天有监测报告,关于冰雹的检验结果仅供参考。
|
图 1 用于产品性能检验的(a)加密自动站和(b)检验站分布 Fig. 1 Distribution of (a) automatic weather stations and (b) verification stations |
文中地图底图基于标准地图服务网站下载的审图号为GS(2019)3082号的标准地图制作,底图无修改。
1.2 检验方法采用强对流业务检验中使用的点-面空间检验方法对预报产品进行检验(唐文苑等,2017;田付友等,2015),即以强对流业务评估中使用的2410个站为基础(图 1b),通过点-面空间检索,搜索检验站周围40 km范围内的相应实况。当检验站或40 km范围内自动站均未有相应的实况,则认为检验站未出现相应的实况,否则,则认为出现了相应的实况。需要注意的是,40 km范围内强对流的实况来源存在明显差别,短时强降水和雷暴大风实况为加密自动站观测,冰雹则来源于灾情报告和监测报告,闪电实况为闪电定位网络的闪电监测。实际处理中,当40 km范围内检索到至少1个站次的短时强降水、雷暴大风和冰雹时,则认为检验站出现了相应的实况,闪电个数则为2个。四类强对流天气的预报结果为0.5°的格点场,通过双线性插值得到检验站点的概率值。在此基础上,根据列联表(表 1),计算临界成功指数(TS)、预报偏差(Bias)、命中率(H)和虚警率(F)检验指标的公式如下:
| $ \mathrm{TS}=\frac{\text { 命中次数 }}{\text { 命中次数 }+ \text { 虚警次数 }+ \text { 空报次数 }} $ | (1) |
| $ \text { Bias }=\frac{\text { 命中次数 }+ \text { 虚警次数 }}{\text { 命中次数 }+ \text { 漏报次数 }} $ | (2) |
| $ H=\frac{\text { 命中次数 }}{\text { 命中次数 }+ \text { 漏报次数 }} $ | (3) |
| $ F=\frac{\text { 虚警次数 }}{{\text { 虚警次数 }}+{\text { 预报无的正确次数 }}} $ | (4) |
|
|
表 1 2×2列联表 Table 1 The 2×2 contingency table |
由于四类强对流的预报结果均是概率性的,则可通过0%~100%的值来表征特定的强对流天气现象出现可能性的大小。在进行确定性预报结果的检验时,以5%作为间隔,分别以格点概率是否超过相应的概率值作为预报有和无的阈值,再结合实况,统计表 1中的各项,并计算TS、Bias、F和H。四个指标中,TS和Bias主要用于确定性性能的评估,F和H用于相对操作特征(ROC)的构建,可同时从确定性和概率的角度评估产品的性能。此外,也通过可靠性图表对四类强对流的概率预报性能进行评估。ROC对Bias不敏感,其评估的是预报产品对两分类事件的区分度(Mason,1982)。一般也会计算ROC曲线右下方的覆盖面积(AUC),当AUC小于0.5时认为预报与气候态相比无技巧,超过0.5则认为是有技巧的预报,1.0则认为是完美的预报(Jolliffe and Stephenson, 2012)。可靠性图表则主要用于预报系统可靠性的评估,展示的是预报概率与相应实况观测频率之间的对应关系(Weisheimer and Palmer, 2014),当且仅当预报系统对所有概率区间的预报都可靠时,预报系统才是可靠的(Tóth et al, 2003)。一般而言,当预报概率与观测频率一致时,预报系统和产品的可靠性才是优秀的。
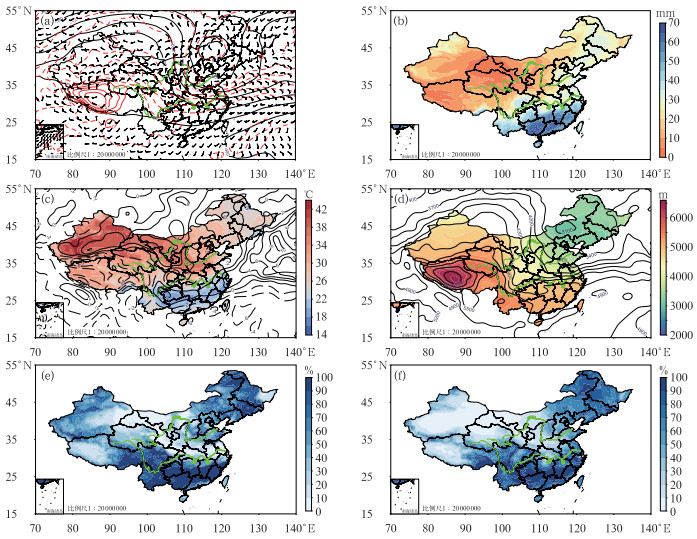
2 2022年6月13日强对流过程中的表现2022年6月13日20时环流形势和物理量场预报显示了有利于多种对流的特征(图 2)。环流形势显示,13日20时500 hPa高压总体较为强盛,我国长江以南地区及中西部大部分地区处于500 hPa上588 dagpm线控制之内,华北及东北有冷涡活动(图 2a),850 hPa风场上显示了从内蒙古东南部向南伸展至山东西部的切变线系统,为北方地区有利于对流的环流背景。与此同时,尽管南方地区500 hPa环流较为平直,但850 hPa上江南南部及华南一带存在弱切变线系统。从大的区域上而言,华北和华南是两个需要关注的潜在强对流区域。整层可降水量显示,江南南部及华南一带总的水汽含量较大,最大位于华南中部一带,在65~70 mm。北方地区整层可降水量整体偏小,仅在东北地区西部至山东东部一带存在30~40 mm的相对大值区域(图 2b)。850 hPa与500 hPa的温差和最有利抬升指数显示(图 2c),北方大部分地区的最有利抬升指数较弱,仅京津冀地区存在负区域,其他地区多在0~2℃。从内蒙古西部至山东西部有一温差大值区。与此同时,东北及华北大部地区的0℃层高度在5000 m以下,为可能出现冰雹区域(图 2d)。而500 hPa(图 2e)和850 hPa(图 2f)相对湿度分布则显示,华南大部分地区的500 hPa和850 hPa大气相对湿度均在90%以上,较为饱和,但东北及华北地区多有干湿相间的分布,即相对湿度大值区内有大量范围较小的不饱和区域存在,在山东西部,850 hPa上甚至显示了明显的东南向伸展的干舌(图 2f)。考虑环流形势和物理量场的配置,以及冷暖交界处常为强对流多发区域,可以判断南北方都有出现雷暴的可能,北方地区需要关注多种强对流天气出现的可能性,并需要关注干环境雷暴大风,南方主要以强降水为主,需要关注湿环境雷暴大风,但南方出现冰雹的可能性较小。
|
图 2 NCEP-GFS 2022年6月12日20时起报的13日20时环流形势和物理量场预报(a)500 hPa高度(黑色等值线,单位:dagpm)、温度(红色等值线,单位:℃)和850 hPa风场(风羽),(b)整层可降水量,(c)850 hPa和500 hPa温差(填色)以及最有利抬升指数(等值线,单位:℃),(d)0℃层高度(填色和等值线,单位:m),(e)500 hPa相对湿度,(f)850 hPa相对湿度 Fig. 2 Forecasting synoptic pattern and parameter field valid at 20:00 BT 13 that initiated at 20:00 BT 12 June 2022 provided by NCEP-GFS (a) 500 hPa geopotential height (black contour, unit: dagpm), temperature (red contour, unit: ℃) and 850 hPa wind field (barb), (b) precipitable water, (c) temperature difference at 850 hPa and 500 hPa (colored) and best lifted index (contour, unit: ℃), (d) 0℃ layer height (colored and contour, unit: m), (e) 500 hPa relative humidity, (f) 850 hPa relative humidity |
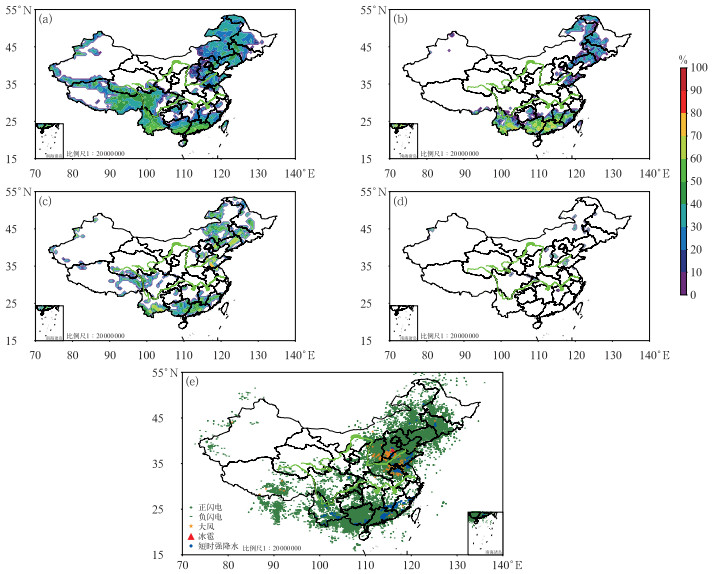
分类强对流客观概率预报落区提供了有针对性的强对流落区参考。2022年6月13日20时的雷暴概率预报显示(图 3a),主要的雷暴关注区域有东北—华北、华南和云南—西藏,新疆西部也有出现雷暴的可能性,且南方地区的雷暴可能性明显高于北方。实况显示(图 3e),东北地区出现了大范围分散性的雷暴,华北地区出现了较为集中的雷暴,南方地区中广东和广西的雷暴均较为明显,云南及西藏也均有雷暴出现,甚至新疆西部和西北部也监测到闪电,表明预报雷暴落区与实况较为一致。与雷暴范围相比,预报的短时强降水范围明显缩小,主要有东北—华北北部和华南—云南两个区域(图 3b),华南短时强降水可能性最大。实况显示华南短时强降水最为显著,云南也有分散性短时强降水出现,华北出现了较为集中的短时强降水,东北地区则出现了零星的分散性短时强降水(图 3e)。雷暴大风的预报显示,吉林—辽宁、山东中西部、华南南部和云南南部均是高概率区(图 3c)。实况显示,华北出现了较为集中的雷暴大风,东北及华南也有分散性雷暴大风出现(图 3e)。雷暴大风预报落区总体准确,但预报区域偏大。冰雹客观预报显示,山东西部和河北西部出现冰雹的可能性较大(图 3d),内蒙古东部也有出现雷暴大风的可能性,但由于缺乏足够的冰雹实况监测信息,不做过多讨论。
|
图 3 2022年6月12日20时起报的13日20时(a)雷暴,(b)短时强降水,(c)雷暴大风,(d)冰雹概率落区预报和(e)13日17—23时的实况分布 Fig. 3 Forecasting probability of (a) thunderstorm, (b) short-time severe rainfall, (c) thunderstorm gale, (d) hail valid at 20:00 BT 13 that initiated at 20:00 BT 12, and (e) the convective phenomena observation during 17:00-23:00 BT 13 June 2022 |
连续分布的检验指标可以反映产品的总体表现。以5%作为间隔,分别计算四类强对流天气不同阈值情况下的TS和Bias。
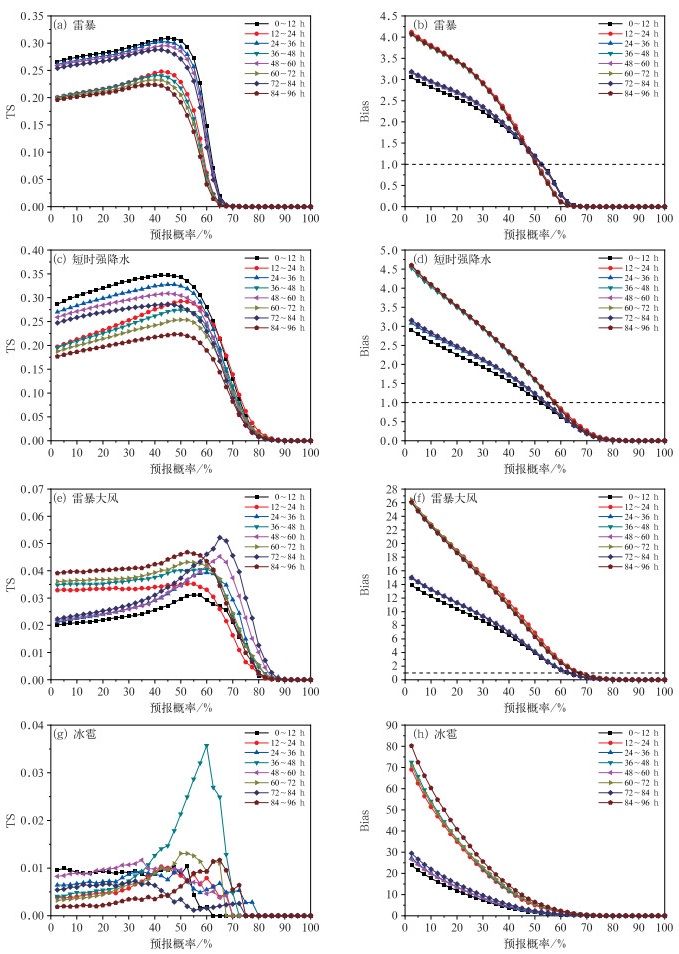
雷暴检验显示了较好的可用性。针对雷暴的TS评分显示(图 4a),同一个预报时次,TS先随预报概率的增大逐渐增大,在40%~50%达到最大,然后随预报概率的增大而逐渐减小,在75%附近接近0.0,之后均维持在0.0。不同预报时效的TS变化具有一致性,但依据预报覆盖的时段(白天和夜间)可显著分为两簇,其中覆盖白天时段的TS中,同一概率值点的TS均高于夜间时段的TS,表明雷暴预报产品在白天有更好的表现。与TS随预报概率的变化不同,不同预报时效的Bias在起始概率处均有最大的预报偏差,通常在3.0~4.5(图 4b)。就单个预报时次而言,随着概率的增加,Bias逐渐减小,在50%概率附近达到1.0的无偏状态,在60%附近接近0.0,表明预报的雷暴概率很少能达到60%以上。与TS变化相对应,Bias也存在显著的与预报覆盖时段是白天还是夜间相关的两簇,但总体有类似的变化特征。对于白天和夜间不同的覆盖时段而言,其最大TS也显著不同,覆盖白天时段的最大TS可达到0.28~0.30,夜间时段的最大TS仅能达到0.22~0.25。
|
图 4 四类强对流天气不同预报时效的TS和Bias随预报概率变化 Fig. 4 Variation of TS and Bias with probability for four convective weather phenomena with different lead times |
短时强降水也有很好的可用性。短时强降水的TS变化与雷暴的TS变化具有类似性,即对于同一个预报时次,TS先随预报概率的增大而增大,达到最大值后快速减小,且很少能预报出超过90%的概率(图 4c)。尽管TS先增后减,但对应的Bias均单调递减,在起始概率处有最大Bias(图 4d)。不同预报时次的最大TS均在50%概率附近取得,对应的Bias在1.5附近。此外,与雷暴类似,短时强降水的TS和Bias也呈现显著的两簇,仍然与预报覆盖的时段是白天还是夜间有关。这一特征很可能与所用的NCEP-GFS资料不能准确反映热力条件和湿度条件的日变化有关。Bhargava et al(2018)研究显示,NCEP-GFS预报白天时段的湿度偏大、温度偏低,而预报夜间时段的湿度偏小、温度偏高,从而使得客观预报得到的分类强对流的检验存在显著的白天—夜间聚类情况。
雷暴大风和冰雹的可用性显著低于雷暴和短时强降水。雷暴大风的TS随预报概率增大仍然呈现先增大后减小的趋势,不同时效的TS在50%~60%达到最大值(图 4e)。对应的Bias仍然在起始概率处取得最大值,最大Bias均超过14,显示了预报明显偏大,然后Bias随概率增大快速减小(图 4f)。与覆盖时段相关的白天和夜间的聚类在不同时效的TS中有一定体现(图 4e),在Bias中有明显的体现(图 4f)。冰雹预报检验显示了更低的可用性,但由于近些年冰雹人工观测的取消,难以获取足够的冰雹实况,且冰雹的局地性更强,因此,本文中冰雹相关的评估结果仅供参考,不做过多讨论。
以最优TS所对应的概率作为提取确定性预报的阈值,是将概率预报转化为确定性预报落区的可行方法(Wilks, 2011)。针对四类不同的强对流天气现象,对不同的预报时效,以取得最大TS时的概率作为阈值,给出四类强对流天气的最优TS和相应的Bias随预报时效的变化(图 5),为制作有针对性的确定性预报提供参考。
|
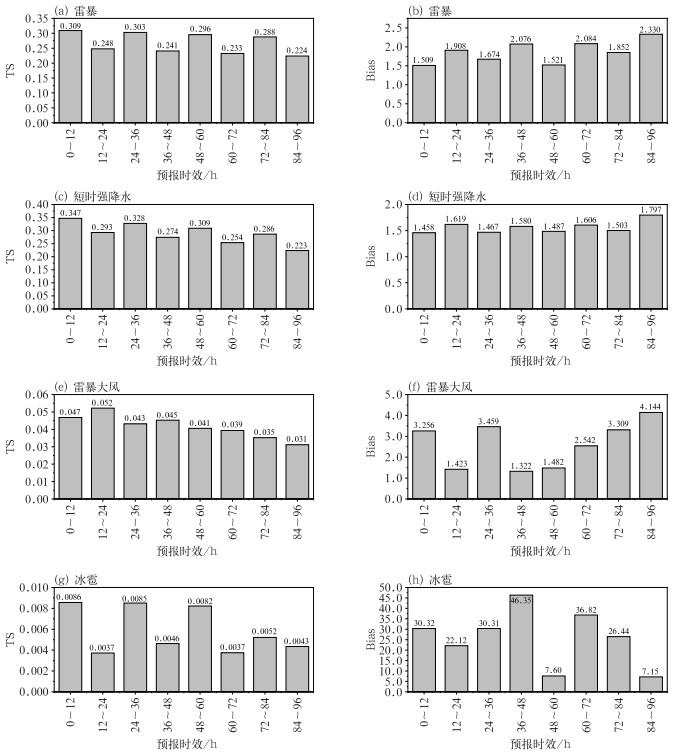
图 5 四类强对流天气不同预报时效的最优TS和相应Bias变化 Fig. 5 Variation of maximum TS and the corresponding Bias for four convective weather phenomena with different lead times |
雷暴确定性TS和Bias均显示了明显的日变化特征,对于相同的覆盖时段,预报时效越短性能越好。覆盖白天时段的TS在0.288~0.309波动(图 5a),对应的Bias波动范围在1.509~1.852(图 5b),覆盖夜间时段的TS在0.224~0.248(图 5a),对应的Bias在1.908~2.330(图 5b)。与夜间时段相比,白天时段的TS略高于夜间,Bias更接近1.0,表明雷暴预报在白天时段的表现优于在夜间时段的表现。唐文苑等(2017)针对覆盖12 h时段的业务雷暴预报的检验中,2010—2015年的雷暴预报TS范围为0.19~0.33,本文的84~96 h时效的夜间时段雷波TS也达到了0.224,表明96 h内的雷暴预报均有很好的可参考性。短时强降水确定性预报的表现甚至优于雷暴确定性预报的表现,尽管短时强降水确定性预报仍然存在与覆盖时段相关的性能波动。覆盖白天时段的短时强降水显示,TS随预报时效的延长逐渐从0.347降低至0.286,夜间时段则逐渐从0.293降低至0.223(图 5c),对应的白天时段的Bias在1.5附近,夜间时段在1.6附近(图 5d)。与此同时,用于对比的业务短时强降水最高TS仅为0.24(唐文苑等,2017),表明本文中的产品性能对业务中的短时强降水预报有较好的可参考性。
雷暴大风确定性预报的表现与雷暴和短时强降水显著不同,TS在数值上低一个量级,且随预报时效的延长呈逐渐减小的趋势,而Bias整体呈逐渐增长的趋势。雷暴大风的最大TS出现在12~24 h时效,为0.052,之后缓慢减小,84~96 h时效为0.031(图 5e), 对应的Bias区间在1.3~4.2(图 5f),显示了明显的预报落区偏大。但雷暴大风TS和Bias没有明显的日变化特征,原因尚不清楚。尽管如此,与业务检验相比,不区分雷暴大风和冰雹的业务预报TS多在0.03,仅在2015年达到0.05(唐文苑等,2017),因此,本研究中的雷暴大风仍然有很好的可参考性。冰雹由于其实况监测方面的原因,检验结果不具有代表性,对相关结论不做过多描述,明显的特征是Bias显著偏大(图 5h),显示了明显的预报落区偏大,但很大可能也与无法收集足够的实况有关。
4 概率性属性评估四类强对流天气的ROC曲线显示了显著不同的性能特征(图 6)。雷暴不同时效的ROC曲线表明(图 6a),所有预报时次的ROC曲线均位于对角线的左上方,显示了一定的可参考性,但在确定性预报中与覆盖时段有关的日变化在ROC中并无明显体现。其次,预报性能随预报时效的延长逐渐减小的趋势在ROC上并无直接体现,因此图 6中也给出了相应的ROC面积AUC。雷暴预报的AUC表明,雷暴预报性能随预报时效的延长整体呈逐渐下降趋势,AUC从0~12 h的0.787逐渐降低至84~96 h时效的0.743,但仍然显著高于0.5的阈值(Jolliffe and Stephenson, 2012),表明96 h内对有无雷暴的预报有较好的区分能力。
|
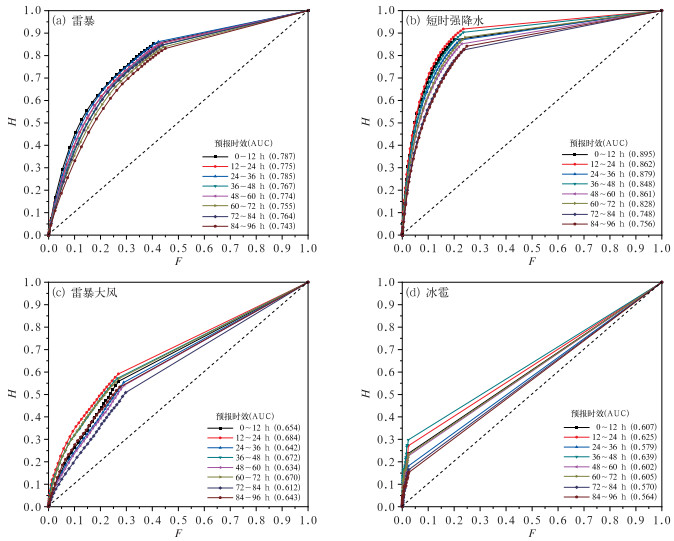
图 6 四类强对流天气不同预报时效的ROC分布 注: 括号内数字为ROC面积AUC。 Fig. 6 Distribution of ROC for four convective weather phenomena with different lead times |
短时强降水的预报能力明显优于雷暴(图 6b)。与雷暴预报相比,ROC曲线更接近左上角。ROC曲线上,覆盖白天时段的表现略优于覆盖夜间时段的表现,AUC上也有更为清晰的体现,覆盖白天时段的AUC均高于其前后时次覆盖夜间时段的AUC(图 6b)。短时强降水的最高AUC达0.895,出现在0~12 h时效,随后波动式下降,但即使是84~ 96 h时效的预报,其AUC也达到了0.756,显示了较好的短时强降水预报能力。
ROC显示雷暴大风的预报性能比雷暴和短时强降水稍差,但仍然具有可用性。所有预报时次的雷暴大风ROC均位于对角线的左上方(图 6c),其显著的不同在于,雷暴大风预报在夜间时段的表现稍优于在白天时段的表现,这在确定性预报中也有所体现,但原因并不清楚。12~24 h时效的雷暴大风AUC最大,为0.684,72~84 h时效最小,为0.612,略高于0.5,表明雷暴大风有一定的可参考性。冰雹预报的ROC是四类强对流天气中最差的,尽管所有预报时次的ROC曲线均位于对角线左上方,但整体均较接近对角线,AUC最大值仅为0.639,出现在第36~48 h时效,最小值为0.564(图 6d)。
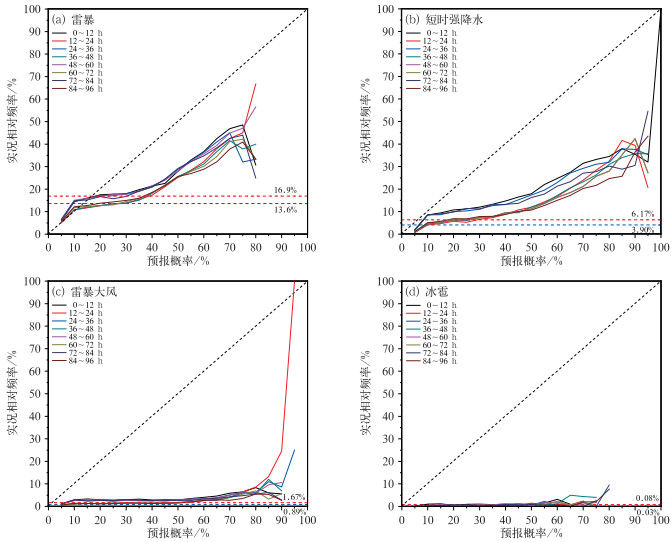
可靠性图表可从另一个角度给出系统可用性的评估。尽管ROC显示四类强对流天气概率预报产品均有一定的识别区分能力,尤其雷暴和短时强降水,但可靠性(图 7)显示,四类强对流天气均存在预报概率偏高的过度预报情况,与图 5中Bias偏大一致。雷暴预报可靠性显示(图 7a),在小于10%的低概率阶段,多个预报时次的曲线沿着对角线分布,预报和实况具有很好的一致性。当预报概率不断增长时,实况观测频率的增长速度显著低于预报概率的增长速度,表明预报概率偏高。尽管如此,白天和夜间时段的雷暴气候平均频次占比分别为16.9%和13.6%,当预报概率超过40%后,线条均位于气候态上方,表明雷暴预报仍然有很好的正技巧。短时强降水与雷暴预报表现类似。尽管与气候态相比,短时强降水预报仍然有很好的可靠性,但在所有概率区间均有明显的过度预报(图 7b),即在所有概率区间,线条均位于对角线的右下方。此外,对于确定性预报中预报技巧随覆盖时段的变化,在雷暴和短时强降水预报的可靠性(图 7a, 7b)中也有体现,尤其是在中间概率区间,在低概率区间和高概率区间这种区别均不明显。雷暴大风和冰雹的过度预报更为显著(图 7c,7d),雷暴大风仅在超过50%的概率区间显示了高于预报概率的性能。需要注意的是,雷暴大风和冰雹的平均监测频率占比均非常小,尤其是冰雹,表明二者相比于雷暴和短时强降水是更为明显的小概率事件,如何更为准确地体现对小概率事件的预报能力,仍然是需要解决的难题(Stephenson et al, 2008;Marzban, 1998)。在本研究中,ROC和可靠性分析共同展示了四类强对流预报产品的可用性,也揭示了后续工作需要改进的方向:改进预报概率过高的情况,使得预报概率和观测频率更为接近。
|
图 7 四类强对流天气不同预报时效的可靠性 注:红色和蓝色水平虚线分别表示白天和夜间时段的实况气候平均值。 Fig. 7 Reliability diagram for four convective weather phenomena with different lead times |
本文介绍了融合物理理解与模糊逻辑人工智能方法的分类强对流客观短期预报系统提供的雷暴、短时强降水、雷暴大风和冰雹四类强对流天气的预报性能,对其在2022年6月13日过程中的表现进行分析的基础上,从确定性和概率性的角度,对2022年4月1日至9月30日每天08时起报的0~96 h内12 h间隔预报产品的确定性和概率性属性特征进行了评估。主要结论如下:
(1) 个例显示,预报系统在短期时效内较为准确给出了雷暴、短时强降水、雷暴大风和冰雹四类不同强对流天气的重点关注区域。
(2) 雷暴和短时强降水确定性预报有很好的可参考性。雷暴和短时强降水的最大TS区间分别为0.224~0.309和0.223~0.347,对应的Bias区间分别为1.509~2.330和1.458~1.797。雷暴大风的性能相对较差,最大TS区间为0.031~0.052,对应的Bias区间为1.322~4.144。
(3) 雷暴和短时强降水的概率预报结果均有较好的可参考性,其中短时强降水概率预报性能更优。雷暴大风和冰雹的概率预报性能相对较差。
(4) 雷暴、短时强降水和雷暴大风预报产品均存在与预报覆盖时效有关的日变化,在确定性检验结果中表现明显,在概率性检验结果中有一定体现。
预报概率偏高的问题在强对流相关研究中也较为常见,如Gard et al(2022)针对脉冲风暴的雷暴研究中,同样发现其预报概率显著高于实况频次的情况。本文中预报概率偏高的过度预报很大可能与预报系统搭建过程中隶属度函数的获取方式有关。当前的隶属度获取方式有很强的主观性,即人为将最高隶属度区间赋予最大1.0的隶属度(Tian et al,2024;2022),与实际情况并不完全相符。如何通过更科学的方法,获取更接近真实状况的隶属度函数,将是后续重点研究的内容之一。关于不同强对流天气预报检验中的日变化,可能由多方面原因引起,如模式对大气环境状态日变化特征的准确描述、实况的日变化特征以及预报方法能否体现相关的日变化特征等,均是需要考虑的问题。此外,需要注意的是冰雹的检验结果仅供参考,由于冰雹实况获取方面的原因,可用的冰雹实况数量远远少于实际出现的冰雹实况数量。
陈法敬, 陈静, 韦青, 等, 2019. 一种基于可预报性的暴雨预报评分新方法Ⅱ: 暴雨检验评分模型及评估试验[J]. 气象学报, 77(1): 28-42. Chen F J, Chen J, Wei Q, et al, 2019. A new verification method for heavy rainfall forecast based on predictability Ⅱ: verification method and test[J]. Acta Meteor Sin, 77(1): 28-42 (in Chinese).
|
刘凑华, 代刊, 林建, 等, 2023. 天气预报全流程检验评估程序库的设计与实现[J]. 气象, 49(3): 351-364. Liu C H, Dai K, Lin J, et al, 2023. Design and implementation of whole process evaluation program library of weather forecast[J]. Meteor Mon, 49(3): 351-364 (in Chinese).
|
唐文苑, 周庆亮, 刘鑫华, 等, 2017. 国家级强对流天气分类预报检验分析[J]. 气象, 43(1): 67-76. Tang W Y, Zhou Q L, Liu X H, et al, 2017. Analysis on verification of national severe convective weather categorical forecasts[J]. Meteor Mon, 43(1): 67-76 (in Chinese).
|
田付友, 郑永光, 孙建华, 等, 2024. 融合物理理解与模糊逻辑人工智能的分类强对流客观短期预报系统: (1)系统构成[J]. 气象, 50(5): 521-531. Tian F Y, Zheng Y G, Sun J H, et al, 2024. Physical understanding and fuzzy logic combined forecasting system for short-term multi-category convective phenomena part Ⅰ: system construction[J]. Meteor Mon, 50(5): 521-531 (in Chinese).
|
田付友, 郑永光, 张涛, 等, 2015. 短时强降水诊断物理量敏感性的点对面检验[J]. 应用气象学报, 26(4): 385-396. Tian F Y, Zheng Y G, Zhang T, et al, 2015. Sensitivity analysis of short-duration heavy rainfall related diagnostic parameters with point-area verification[J]. J Appl Meteor Sci, 26(4): 385-396 (in Chinese).
|
王新敏, 栗晗, 2020. 多数值模式对台风暴雨过程预报的空间检验评估[J]. 气象, 46(6): 753-764. Wang X M, Li H, 2020. Spatial verification evaluation of typhoon rainstorm by multiple numerical models[J]. Meteor Mon, 46(6): 753-764 (in Chinese).
|
郑永光, 林隐静, 朱文剑, 等, 2013. 强对流天气综合监测业务系统建设[J]. 气象, 39(2): 234-240. Zheng Y G, Lin Y J, Zhu W J, et al, 2013. Operational system of severe convective weather comprehensive monitoring[J]. Meteor Mon, 39(2): 234-240 (in Chinese).
|
Bhargava K, Kalnay E, Carton J A, et al, 2018. Estimation of systematic errors in the GFS using analysis increments[J]. J Geophy Res Atmos, 123(3): 1626-1637.
|
Casati B, Wilson L J, Stephenson D B, et al, 2008. Forecast verification: current status and future directions[J]. Meteor Appl, 15(1): 3-18.
|
Ebert E E, 2008. Fuzzy verification of high-resolution gridded forecasts: a review and proposed framework[J]. Meteor Appl, 15(1): 51-64.
|
Gard T L, Fuelberg H E, Cintineo J L, 2022. The utility of ProbSevere v2.0 for predicting pulse severe thunderstorms[J]. Wea Forecasting, 37(9): 1601-1613.
|
Gilleland E, Ahijevych D, Brown B G, et al, 2009. Intercomparison of spatial forecast verification methods[J]. Wea Forecasting, 24(5): 1416-1430.
|
Jolliffe I T, Stephenson D B, 2012. Forecast Verification: A Practitioner's Guide in Atmospheric Science[M].
Hoboken: Wiley & Sons, Ltd: 292.
|
Kok K, Schreur B W, Vogelezang D, 2008. Valuing information from mesoscale forecasts[J]. Meteor Appl, 15(1): 103-111.
|
Marzban C, 1998. Scalar measures of performance in rare-event situations[J]. Wea Forecasting, 13(3): 753-763.
|
Mason I B, 1982. A model for assessment of weather forecasts[J]. Australian Meteor Mag, 30(4): 291-303.
|
Stephenson D B, Casati B, Ferro C A T, et al, 2008. The extreme dependency score: a non-vanishing measure for forecasts of rare events[J]. Meteor Appl, 15(1): 41-50.
|
Tian F Y, Xia K, Sun J H, et al, 2024. Ingredients-based methodology and fuzzy logic approach combined short-term short-duration heavy rainfall forecasting: an improved scheme[J]. J Trop Meteor. DOI:10.3724/j.1006-8775.2024.022
|
Tian F Y, Zhang X L, Xia K, et al, 2022. Probability forecasting of short-term short-duration heavy rainfall combining ingredients-based methodology and fuzzy logic approach[J]. Atmosphere, 13(7): 1074.
|
Tóth Z, Talagrand O, Candille G, et al, 2003. Probability and Ensemble Forecasts[M]//Joliffe I, Stephenson D. Forecast Verification: A Practitioner's Guide in Atmospheric Science. Hoboken: John Wiley & Sons: 137-163.
|
Weisheimer A, Palmer T N, 2014. On the reliability of seasonal climate forecasts[J]. J Roy Soc Interface, 11(96): 20131162.
|
Wilks D S, 2011. Statistical Methods in the Atmospheric Sciences: 3rd ed.[M].
San Diego: Academic Press.
|
Yano J I, Soares P M M, Köhler M, et al, 2015. The convective parameterization problem: breadth and depth[J]. Bull Amer Meteor Soc, 96(8): ES127-ES130.
|
 2024, Vol. 50
2024, Vol. 50 