引言

预报稳定性是指两次预测对某一事件的发生时间、持续时间或空间范围的一致程度(Pappenberger et al，2011)，在气象中从一个发布时间到下一个发布时间预报的变化程度是衡量预报系统性能的一个重要方面(Zsoter et al，2009；Griffiths et al，2019)。持续性的稳定预报对于成功地预测极端降水事件具有重要的作用，Buizza et al(2017)调查了2000年10月14—16日发生在意大利北部的一场极端天气过程(1951年以来波河最严重的洪水)，指出了一致性预报的重要性。较大的不稳定性意味着不同时效降水量预报的“反复无常”，增加了应用决策难度。因此，在天气预报业务中评估模式的稳定性，使用者能够正确认识不同数值预报模式产品性能，可以有针对性地对产品加以订正，从而提高业务预报准确性。

学者们开发了翻转指数、收敛指数、不一致指数等用以代表多次预测的变化程度。Zsoter et al(2009)提出了不一致性指数(纬度加权均方根误差)，该指数基于区域平均的连续两个预测序列差值与两次预报的平均标准差之比，较好地描述了前后两次预报之间的不一致性。Ruth et al(2009)定义了预测收敛分数，通过统计“预报跳跃”的次数进行不一致性分析，反映的是前后两次预报之间的偏差随时效的变化特征。Ehret(2010)定义了收敛指数，包含不同起报时次预报结果与预报时刻实况结果的偏差随预报时效变化情况，采用收敛(即连续多次预报趋于实况)和波动(即连续多次预报在实况附近上下波动)两个标准衡量预报的不一致性问题，体现的是前后两次预报的误差随时效变化特征。McLay(2011)研究了360 h时效内24 h间隔的共15个预报时效的稳定性，将相邻时效之差求最大值，然后利用百分位甄别出最不稳定和最稳定的情况。为了对预报趋势的翻转性进行量化，Griffiths et al(2019)在前人的基础上开发了Flip-Flop指数，该指数能够定量计算降水量变化趋势的翻转程度大小，并且不惩罚单调递增或递减的序列，可以用于比较不同时间或空间尺度以及不同周和季节的预报特征。目前国内研究较多的是基于国外的研究方法开展的应用，郭换换等(2016b)给出了Zsoter et al(2009)提出的不一致指数、Ehret(2010)定义的收敛指数、Lashley et al(2008)和Ruth et al(2009)提出的预报收敛分数以及Toth et al(2003)提出的基于Talagrand分布的时间一致性直方图等几种研究不一致方法的综述。郭换换等(2016a)、郭达烽等(2018)、智协飞等(2018)、夏旻惠和智协飞(2020)采用Zsoter et al(2009)提出的方法对ECMWF业务预报模式地面气温以及TIGGE资料中ECMWF、NCEP、CMA 3个预报系统的东亚地面气温、500 hPa位势高度场、海平面气压场等要素预报的不一致性特征进行了研究。以上学者开展的研究，或评估的是连续2个预报时效的不一致性，或不体现单调递增/单调递减等特征，或者未考虑不同气候背景下降水量级差异等情况。

本文改进了Flip-Flop指数(改进后简称FF_norm)，使用相对标准偏差指标计算降水量波动大小，使用FF_norm指数衡量降水量预报趋势的翻转程度以及变化趋势稳定性等，研究在实况有降水和暴雨及以上两种降水情况下，5种模式对中国6个气候分区(熊敏诠，2017)的随时效临近降水量预报的变化特征，以探讨多个业务常用模式多个连续时效降水量预报趋势的稳定性，为预报以及模式的改进提供参考。

1 参与检验的模式及资料 1.1 参与检验的模式介绍

欧洲数值预报中心(ECMWF)和美国国家环境预报中心(NCEP-GFS)是目前国内预报业务最常参考和应用的全球数值模式，中国气象局区域中尺度天气数值预报系统(CMA-MESO)和华东区域气象中心高分辨率数值模式(CMA-SH9)是业务常用的区域模式(辛辰和漆梁波，2018；王晓峰和周荣卫，2021；苏翔等，2022；刘静等，2022)。其中，ECMWF 2016年3月8日起进行了全面升级(Hólm et al，2016)，此后不间断进行IFS循环和同化等方面更新(Buizza et al，2017；Diamantakis and Váňa，2022)；NCEP-GFS最近的两次升级分别在2019年6月和2021年3月(https://www.emc.ncep.noaa.gov/users/meg/home/future.html[2021-3-18])；GRAPES_MESO v4.0版本包含了分辨率的提高、模式动力框架和物理过程改进以及有效应用雷达资料的云分析系统的引入(沈学顺等，2020)，雨带分布更接近观测，能够更好地描述降水细节分布(黄丽萍等，2017)，2021年10月该模式停止下发产品，升级改进后的系统为CMA-MESO 3 km(CMA-MESO v5.1)；CMA-SH9 2.0版利用ADAS同化系统有效融合了全国雷达基数据、FY红外和可见光数据等在内的多源资料，采用了复杂的云分析，并在模式物理过程等方面较上一版本进行大量改进(吕林宜等，2019)。参与对比的还有山东省气象科学研究所逐半小时同化预报系统(HHUPS-ST)，该系统于2020年1月1日正式运行，每12小时更换一次背景场，每半小时同化一次数据等。模式动力框架、资料同化、参数化方案以及时空分辨率等的不同，可能会使得不同模式的稳定性存在差异。各模式产品的主要特征见表 1。参与检验的模式资料为每日08时(北京时，下同)和20时起报的24、36、48、60和72 h时效的降水量预报产品，检验时段为2020—2021年6—9月。

1.2 实况观测资料

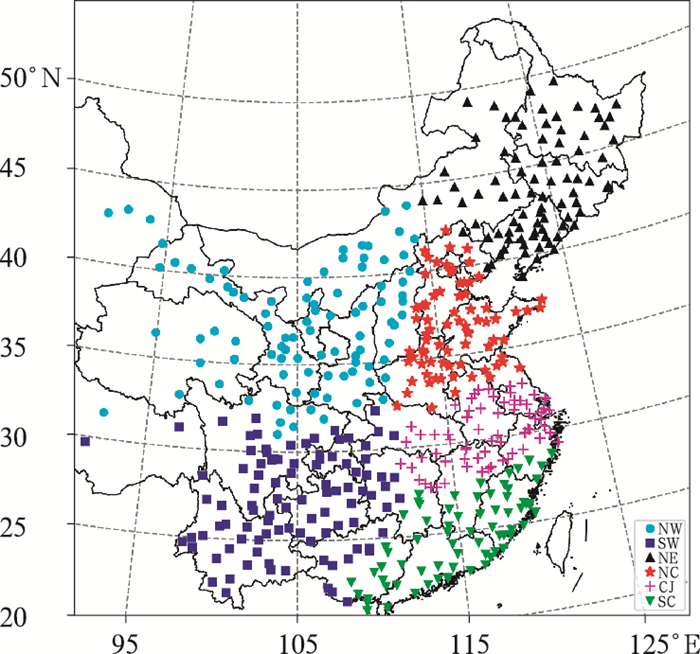
由于我国东临太平洋、西接欧亚大陆，为季风气候，降水量具有区域性特征，因此本文采用熊敏诠(2017)利用近60年中国日降水量资料得到的分区进行稳定性评估。研究的区域包括西北区(简称NW)、西南区(简称SW)、东北区(简称NE)、华北区(简称NC)、长江中下游地区(简称CJ)和华南区(简称SC)。分区及站点分布如图 1所示。实况资料采用熊敏诠(2017)选取的484个国家级(地面)气象观测站，研究的时间段为2020—2021年汛期(6—9月)。

本文对24 h累计降水量(实况20时至次日20时)进行模式预报的稳定性评估，分为实况有降水(24 h降水量大于等于0.1 mm)、暴雨及以上降水(24 h降水量大于等于50 mm)2种情况。另外，当实况有降水时，单站样本数最少为11 d，最多为194 d，全部样本参与统计评估；当实况为暴雨及以上的强降水时，由于该降水等级天气相对较少，筛掉样本数不足5 d的样本，选取≥5 d的站点进行分析。

2 方法 2.1 相对标准偏差

相对标准偏差(RSD)又叫标准偏差系数、变异系数、变动系数等，公式如下：

$ \operatorname{RSD}=\frac{\sqrt{\frac{1}{n-1} \sum\limits_{i=1}^n\left(f_i-\bar{f}\right)^2}}{\bar{f}} $

(1)

式中: f_i代表某个时效的降水量预报值，f代表多时效预报的平均值，n为参与检验的时效个数，文中选取了24、36、48、60和72 h共5个时效。本文将RSD用于多时效降水量预报的波动性特征分析，与标准偏差(用以衡量数据值偏离算术平均值的程度)相比，相对标准偏差能够去除样本平均值差异的影响，有利于消除不同气候背景的差异性，RSD值越大说明多时效的降水量预报波动性越大。然而，该方法不能反映降水量预报变化趋势的特征。

2.2 Flip-Flop_norm指数

为了研究多时效预报变化趋势的稳定性，Griffiths et al(2019)提出了Flip-Flop指数(简称FF指数)，该指数能够定量化地给出多时效降水量预报趋势的翻转幅度，公式如下：

$ \mathrm{FF}=\frac{1}{n-2}\left\{\sum\limits_{i=1}^{n-1}\left|f_i-f_{i+1}\right|-A\right\} $

(2)

$ A=\max f_i-\min f_i $

(3)

式中：f_i代表某个时效的降水量预报值，f_i+1代表与f_i相邻时效的预报值，maxf_i代表所有时效中预报的降水量最大值，minf_i代表所有时效中预报的降水量最小值，n为参与检验的时效个数。指数的范围区间为[0，A]，当指数为0时，表示预报值随时效的临近单调递增或递减；指数越大说明降水量变化趋势的翻转程度越大；指数的最大值A为多个预报时效中的降水量最大值与最小值的差。以24、36、48 h时效为例，降水量的预报值分别为f₂₄、f₃₆、f₄₈，当f₂₄≤f₃₆≤f₄₈或f₂₄≥f₃₆≥f₄₈时，表示随时效的临近降水量预报单调递减或递增，如果f₃₆与f₂₄和f₄₈相比是一个异常大或者小的值，那么FF指数代表f₃₆分别与f₂₄和f₄₈之间的差异较小的值，该值越大，预报值的翻转程度越大。

由于FF指数值受降水量大小影响较大，而不同区域降水量差异显著，为消除降水量差异产生的干扰，本文对FF指数进行了改进，将其进行归一化处理，改进后称为Flip-Flop_norm指数，简称FF_norm指数，改进后的公式如下：

$ \mathrm{FF}_{\text {norm }}=\frac{1}{n-2}\left\{\frac{\sum\limits_{i=1}^{n-1}\left|f_i-f_{i+1}\right|}{A}-1\right\} $

(4)

式中f_i、f_i+1和n同公式(2)，具体参与检验时效同2.1节，该指数的区间范围是[0，1]，当指数为0时，表示预报值随时效的临近单调递增或递减，随着指数的增大，预报降水量的翻转程度越大。

以2021年8月12日20时至13日20时过程为例(表 2)，ECMWF、NCEP-GFS和HHUPS-ST模式60 h和48 h时效降水量预报较72 h明显增大，随着时效的临近，36 h和24 h时效预报的降水量再减小，因此5个时效(72~24 h)的预报呈现增加—减小的波动趋势，而CMA-MESO、CMA-SH9则是从72~24 h的降水量预报基本为单调递减的，因此其FF_norm明显小于ECMWF、NCEP-GFS和HHUPS-ST。

3 多种模式预报稳定性特征分析 3.1 相对标准偏差分布特征

通过统计有降水时各模式多时效的相对标准偏差可知，全球模式ECMWF和NCEP-GFS的相对标准偏差均较小，分别为0.586、0.594。区域模式的相对标准偏差较大，其中CMA-MESO最大为0.926，其次是CMA-SH9为0.903。总体而言，全球模式随时效临近预报的降水量波动幅度小于区域模式。

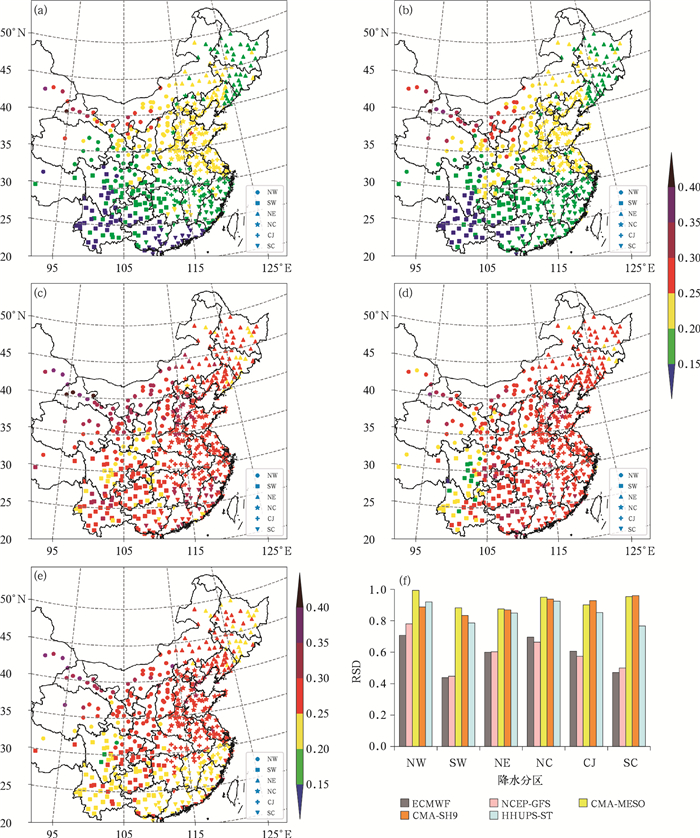
图 2给出的是有降水时不同区域的5种模式的多时效降水预报的相对标准偏差空间分布及其区域平均值特征。全球模式ECMWF(图 2a)和NCEP-GFS(图 2b)的相对标准偏差均较小，其预报的最小区域位于SW、SC的西部和南部(小于0.4)，其次是SC的大部地区、NE的东部、NW的南部和CJ的中游地区，在0.4~0.6，相对标准偏差较大的地区位于NC、NE的中西部，为0.6~0.8，最大的区域位于NW的西北部，大于0.8。区域模式中HHUPS-ST(图 2e)的相对标准偏差相对较小，在SW、SC和NE的东部地区较小，为0.6~0.8，其他区域基本大于0.8，其中NW的西北部最大值达1.35；CMA-MESO(图 2c)和CMA-SH9模式(图 2d)的相对标准偏差相对较大，在SW和NE的部分地区以及NW的南部相对较小，为0.6~0.8，其他区域大于0.8，其中NC、SC、CJ和NW均有站点相对标准偏差大于1.2，2种模式的最大值均位于NW的西北部。

结合不同区域平均的相对标准偏差(图 2f)可知，ECMWF对NW、SW、NE、SC和NCEP-GFS对NC、CJ区域的相对标准偏差相对较小，CMA-MESO模式对NW、SW、NE、NC和CMA-SH9对CJ、SC区域的相对标准偏差相对较大。各模式对SW的西部和NE的东部以及SC的南部预报的波动幅度较小，对西北区的西部预报的波动幅度较大。

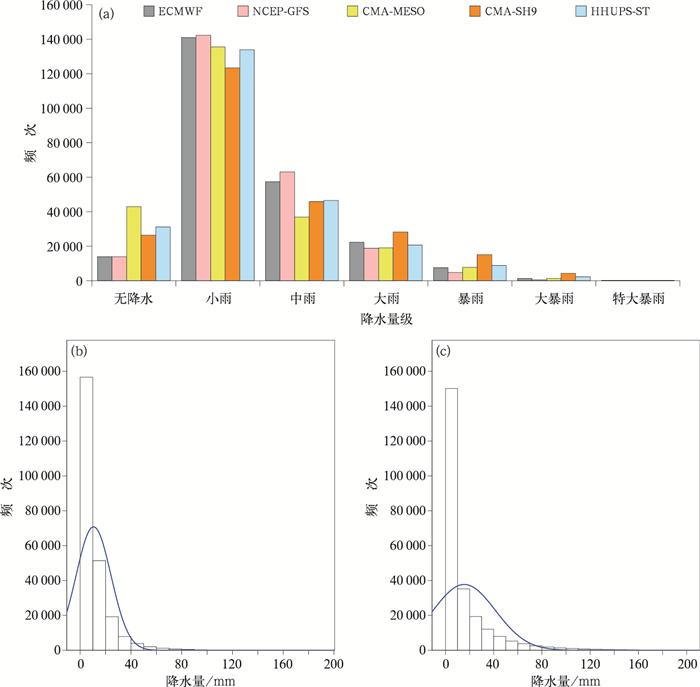
为了探索不同模式相对标准偏差指标存在差异的原因，本文分析了各模式降水量预报量级分布特征。统计表明，在实况有降水的情况下，多种模式全部时效的不同降水量级预报的频次(图 3a)特征为：各模式预报的降水量级频次峰值均为小雨，随着降水量级增大频次迅速降低；全球模式对小雨和中雨的预报次数最多，区域模式对大雨、暴雨和大暴雨的次数相对较多；对于预报无降水而言，区域模式尤其是CMA-MESO 72~36 h时效未预报降水的次数远远高于其他模式。以NCEP-GFS(图 3b)和CMA- SH9(图 3c)为例分析了不同模式降水预报的频次分布特征，结果显示，CMA-SH9频次分布较宽，尤其是对70 mm以上降水量的预报频次显著大于NCEP-GFS，这与区域模式对局地大降水有更强的反应能力有关。以上表明，区域模式降水预报的局地性特征更加明显，是其相对标准偏差指标大于全球模式的可能原因之一。

3.2 FF_norm指数特征对比分析

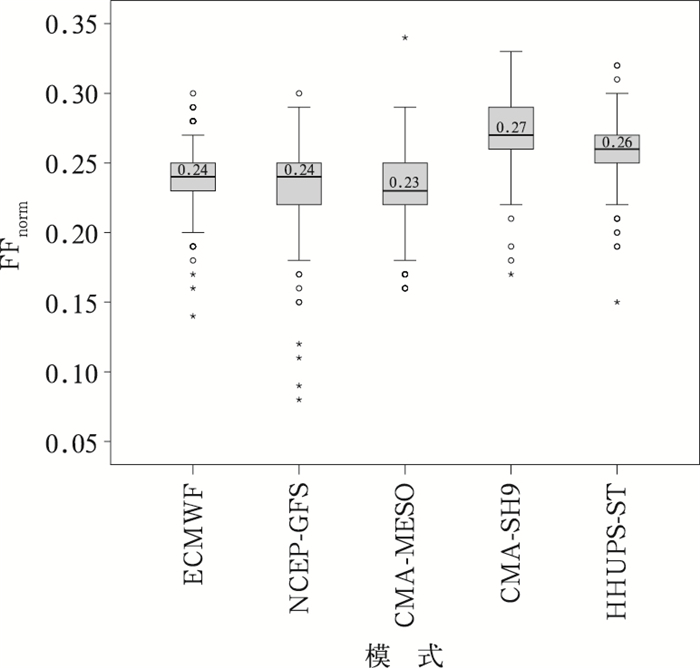
采用箱线图对实况有降水时多种模式的FF_norm指数进行综合分析(图 4)，CMA-MESO指数的中位数最小, 为0.23；NCEP-GFS和ECMWF指数的中位数相同, 为0.24，只是ECMWF的整体分布比NCEP-GFS更加集中，说明ECMWF对各站的稳定性预报特征较为一致；HHUPS-ST的中位数为0.26；CMA-SH9的中位数最大，为0.27，且整体高于其他模式。总的来说，CMA-MESO多时效降水预报趋势的稳定性最好，其后依次是ECMWF、NCEP-GFS和HHUPS-ST，CMA-SH9多时效降水预报趋势的稳定性最差。

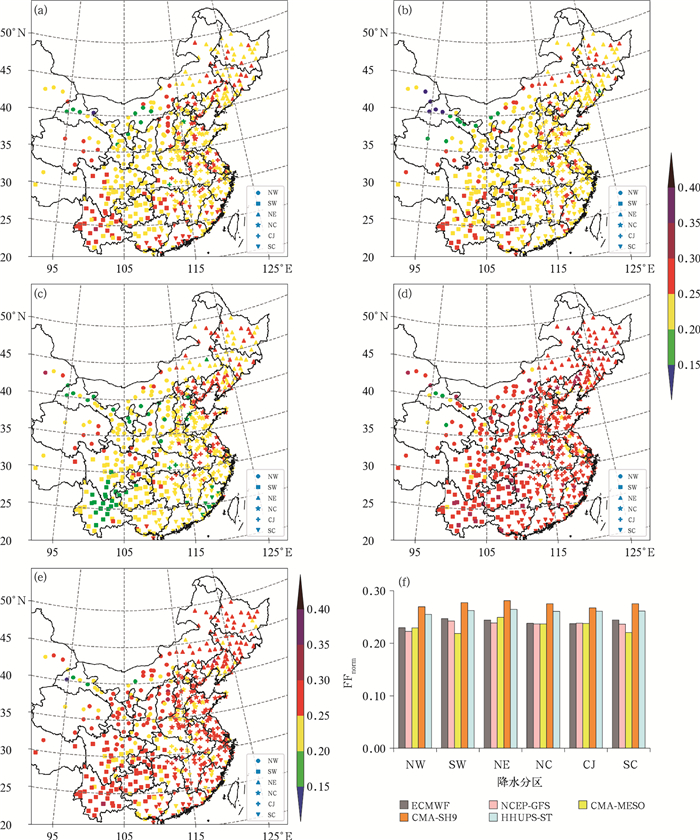
下面探讨当实况有降水时，多个模式对各降水分区的FF_norm指数预报特征。CMA-MESO(图 5c)在各区均有FF_norm指数小于0.20的站点，尤其是SW的站点数最多，SC的南部和NW的西部指数均较小，指数较大的站点位于NE的北部和南部地区、CJ的下游地区以及NC的北部地区，在0.25~0.30。ECMWF模式(图 5a)FF_norm指数小于0.20的站点主要位于NW，指数较大的站点(0.25~0.30)主要位于SW的西部、NE的中东部、NC的西部、CJ的下游地区和SC的西南部。NCEP-GFS(图 5b)在NW有部分站点FF_norm指数较小，小于0.20，NCEP-GFS在各区均有0.25~0.30的指数较大站点，其中在CJ、SW的西南部和NE的北部的站点数最多。HHUPS-ST(图 5e)仅有4个位于NW的站点FF_norm指数小于0.20，大部分区域指数在0.20~0.30，在NW、SW、NE和CJ区域均有少量站点的指数大于0.30。CMA-SH9(图 5d)仅3个站点(NW区)FF_norm指数小于0.20，大部分区域指数≥0.25，且是各模式中指数大于0.30的站点数最多的，其中位于SW的站点数最多，SC的南部以及NW、NE和NC的交界处也有较多的站点分布。

综合区域平均的FF_norm指数(图 5f)可得出以下结论：各区均为CMA-MESO、NCEP-GFS、ECMWF的降水量预报趋势稳定性指数小于CMA-SH9和HHUPS-ST；CMA-MESO对SW和SC的预报趋势稳定性指数明显小于其他模式，NCEP-GFS对NW、NE的FF_norm指数最小，降水量预报趋势的稳定性较好；CMA-SH9对于6个区域的FF_norm指数均最大，说明CMA-SH9随着时效的临近降水预报趋势的翻转程度较大，降水预报趋势不够稳定，尤其是对NE的降水预报趋势的稳定性较差。

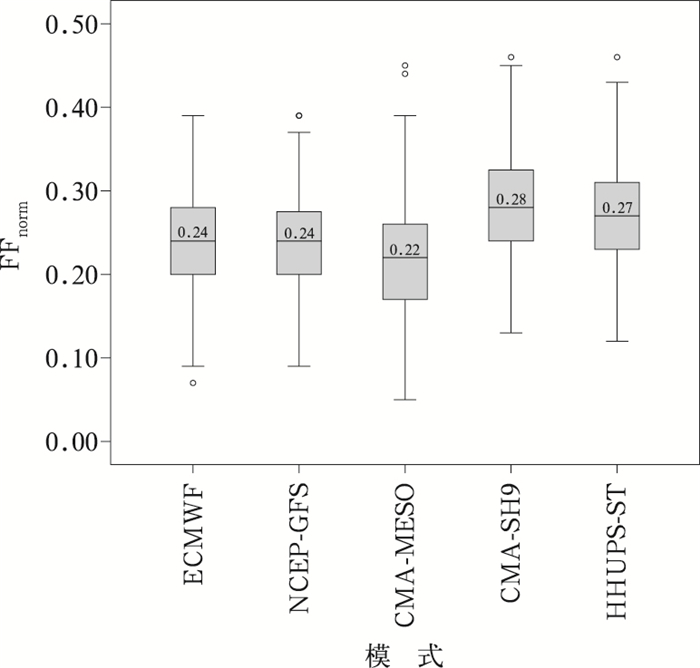
当实况为暴雨及以上量级降水时，多种模式FF_norm指数的综合分布情况(图 6)为：CMA-MESO模式FF_norm指数的中位数最小，为0.22；NCEP-GFS和ECMWF模式指数的中位数相同，为0.24；HHUPS-ST模式指数的中位数为0.27；CMA-SH9模式指数的中位数最大，为0.28，整体高于其他模式。与有降水时的特征一致，CMA-MESO降水预报趋势的稳定性最好，CMA-SH9降水预报趋势的稳定性最差。

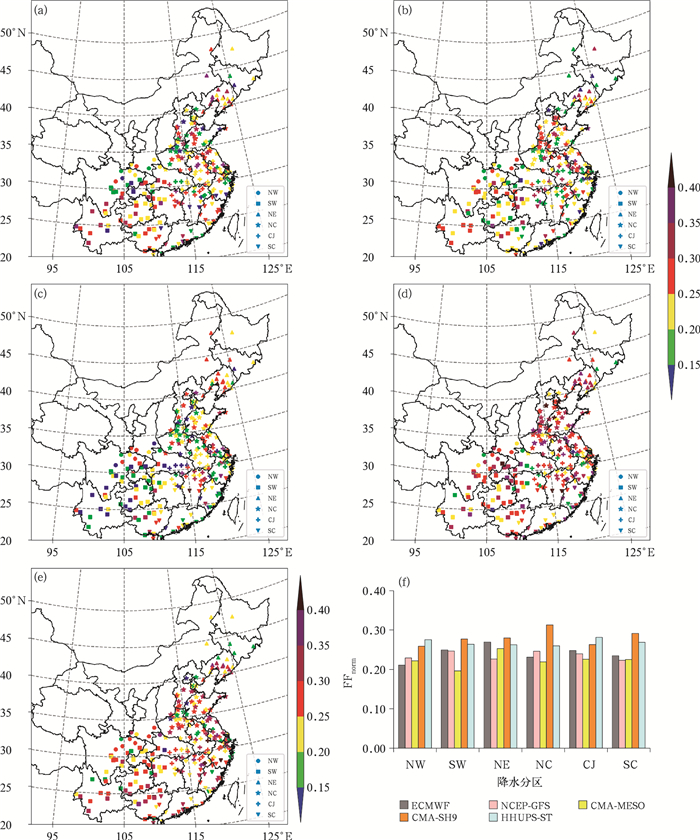
分析多种模式对不同区域的暴雨及以上降水预报的FF_norm指数空间分布可知，小于0.15的站数为CMA-MESO(图 7c)最多(23个)，其次是ECMWF(图 7a)为18个，NCEP-GFS(图 7b)为11个，HHUPS-ST(图 7e)为4个，CMA-SH9(图 7d)最少为2个。

CMA-MESO模式的FF_norm指数在5种模式中相对较小，指数小于0.15的区域位于SW、CJ的中游和NC西部的部分地区，此外，各个区域均有指数大于0.3的站点，其中CJ的站数较多，最大值位于NE的辽宁省；其次是ECMWF和NCEP-GFS模式，ECMWF模式FF_norm指数小于0.15的站点主要分散在NC、SC和SW的局部地区，而在SW、NE、NC、CJ和SC区域均有大于0.3的站点，其中SW和CJ区所占的站数相对较多，指数最大位于CJ，NCEP-GFS模式FF_norm指数小于0.15的站点主要位于CJ下游的浙江省，除NW外，其他区均有大于0.3的站点，其中CJ的站数最多，其次是SW的中东部，指数最大位于CJ；HHUPS-ST模式FF_norm指数小于0.15的站点位于NC的西部地区，各区均有大于0.3的站点，其中CJ的站数最多，其次是NC和SW，指数最大位于SW的东南部；CMA-SH9在5种模式中大于0.3的站数最多，其中位于NC的站数最多，其后依次是SW、SC和CJ，指数最大的站点位于NC的北部。上述分析表明，对暴雨及以上降水，各模式在不同区域的预报趋势稳定性指数差异较大，而对CJ的随时效临近降水预报趋势的稳定性均较差。

结合区域平均(图 7f)可以得出，与有降水时的预报特征相似，各区FF_norm指数均为CMA-MESO、NCEP-GFS、ECMWF小于CMA-SH9和HHUPS-ST模式；CMA-MESO对SW、NC、CJ和NCEP-GFS对NE、SC以及ECMWF对NW的FF_norm指数明显小于其他模式，降水预报趋势的稳定性较好；CMA-SH9对于大部分区域的FF_norm指数均最大，尤其是对NC降水预报趋势的稳定性较差。

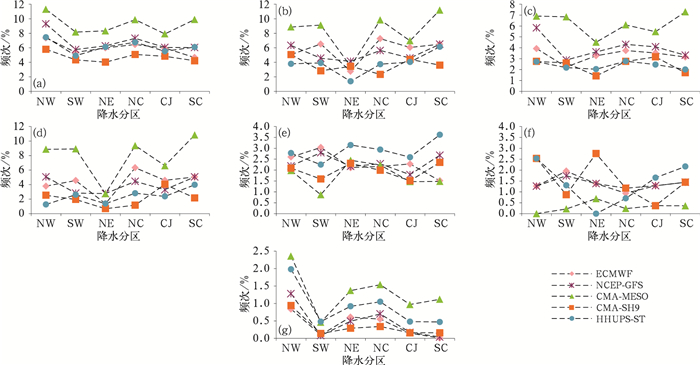
4 降水量预报变化趋势稳定的频次特征分析

多时效降水量预报变化趋势稳定频次是指各模式随时效的临近，预报的降水量单调递增、递减或均预报无降水的次数。图 8a为当实况有降水时，各模式降水量预报变化趋势稳定的频次分布，CMA-MESO对各区的变化趋势稳定预报频次均最多，显著高于其他模式，其次是NCEP-GFS，HHUPS-ST和ECMWF的变化趋势稳定预报频次比较接近，最低为CMA-SH9。各模式对于NW的变化趋势稳定预报频次均较高。当实况为暴雨及以上降水时，模式预报变化趋势稳定的频次分布如图 8b所示，CMA-MESO对NW、SW、NC、CJ和SC预报的总频次最多，NCEP-GFS对NE预报的总频次最多，CMA-SH9对SW、NC和SC预报的频次最少，HHUPS-ST对NW、NE和CJ预报的频次最少。

进而分析随时效临近模式预报的降水量单调递增(图 8c, 8d)和递减(图 8e, 8f)特征，结合单调递增与递减频次的差值(表 3)来看，无论是何种降水，CMA-MESO和NCEP-GFS对各区的预报均为随时效临近预报的降水量单调递增次数大于递减的，且CMA-MESO对NW、SW、NC、CJ和SC的单调递增次数显著大于其他模式。ECMWF在NW、NE、NC、CJ和SC区域对有降水的预报单调递增次数大于递减的，在SW区的预报相反；对各区暴雨及以上降水的预报均为单调递增次数大于递减的，尤其是对NC的预报。CMA-SH9在有降水时，对NW、NC、SW和CJ区域预报的单调递增次数略大于递减次数，对NE和SC区域的预报则相反；关于暴雨及以上降水的预报在CJ单调递增大于递减，在NE的预报相反，其他地区单调递增和递减次数基本一致。HHUPS-ST对各区降水的预报均为随着时效临近降水量单调递减大于递增次数，在NW、NE、NC、CJ和SC递减的次数大于其他模式；对暴雨及以上降水的预报在大部分地区预报的递增次数大于递减的(NW除外)。

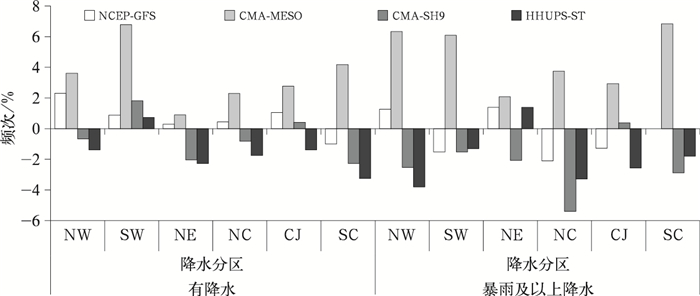
在此基础上，为了部分消除气候背景和样本局限性的影响，以ECMWF作为参考对象，考察NCEP-GFS、CMA-MESO、CMA-SH9和HHUPS-ST模式随时效临近降水量预报单调递增与递减的情况(图 9)。总体上，NCEP-GFS的单调递增与递减频次的差值比较接近ECMWF；CMA-MESO的频次差值大于ECMWF，随时效临近降水量预报逐渐增大的特征比较明显；CMA-SH9和HHUPS-ST在大部分区域预报的频次差值比ECMWF偏小，尤其是有降水时，HHUPS-ST随着时效临近逐渐减小频次大于逐渐增加频次。

图 8g为当实况有降水时，模式的多时效降水预报量均为0 mm的频次分布，CMA-MESO对各区预报的频次均最多，其次是HHUPS-ST，CMA-SH9预报的频次相对最少。各模式对NW预报的频次最高，对SW和SC预报的频次相对较低。当实况为暴雨及以上降水时(图略)，各模式基本上未有预报降水量为0 mm的情况。

以上分析表明，当实况有降水时，CMA-MESO预报的降水量随时效临近单调递增、递减和预报无降水的总次数均最多，其次是NCEP-GFS，并且该2种模式对各区的降水量预报均为随时效临近递增次数大于递减的，稳定预报频次最少的是CMA-SH9；当实况为暴雨及以上降水，CMA-MESO在大部分地区的稳定预报频次最高，各模式基本为单调递增次数大于递减次数；以ECMWF模式为基准，CMA-MESO随时效临近单调递增与单调递减的差值大于ECMWF，NCEP-GFS与ECMWF较为接近，CMA-SH9和HHUPS-ST模式在大部分区域小于ECMWF。

5 结论与讨论

为更好地了解不同数值模式降水预报产品性能，本文深入研究了业务常用的全球模式ECMWF、NCEP-GFS以及区域模式CMA-MESO、CMA-SH9、HHUPS-ST预报的稳定性。采用相对标准偏差指标计算不同时效降水量预报波动大小、改进并使用FF_norm指数衡量降水量预报趋势的翻转程度以及变化趋势稳定预报的频次等方法，分实况有降水、暴雨及以上降水2种情况，对5种模式在中国6个气候分区汛期(6—9月)降水预报的稳定性特征进行了分析。主要结论如下：

(1) 当实况有降水时，全球模式多时效降水预报的相对标准偏差小于区域模式，即全球模式降水量预报波动相对较小，这可能与全球模式降水量频率分布较窄，对大雨及以上降水预报频次相对较少，区域模式降水量频率分布较宽，降水量预报局地性特征更加显著有关。各模式对西南区的西部、东北区东部以及华南区的南部预报的波动性较小，对西北区的西部预报的波动性较大。

(2) 就降水预报趋势的稳定性而言，2种降水情况下均为CMA-MESO、NCEP-GFS和ECMWF的稳定性较好，FF_norm指数小于HHUPS-ST和CMA-SH9，CMA-SH9对各区的FF_norm指数最大、降水量预报变化趋势稳定性较差。当实况有降水时，各模式均对西北区的西北部预报趋势的稳定性最好，此外，CMA-MESO对西南区、华南区南部降水量预报变化趋势的稳定性较为突出；当实况为暴雨及以上降水时，CMA-MESO对西南区、NCEP-GFS对华南区的预报稳定性最好。各模式对长江中下游地区的指数相对较大，多时效降水预报趋势的稳定性较差。

(3) 趋势稳定预报(单调递增、递减或均预报无降水)的频次特征为：有降水时，CMA-MESO预报的降水量随时效临近单调递增、递减和预报无降水的总次数均最多，其次是NCEP-GFS，此2种模式对各区的降水量预报均为随时效临近递增次数大于递减的，且CMA-MESO以单调递增为主，稳定预报频次最少的是CMA-SH9；暴雨及以上降水时，CMA-MESO在大部分地区的稳定预报频次最高(仅NCEP-GFS在东北区次数最多)，各模式基本为单调递增次数大于递减次数(CMA-SH9对东北区、HHUPS-ST对西北区预报除外)；以ECMWF作为参考对象，NCEP-GFS与ECMWF较为接近，CMA-MESO随时效临近单调递增与递减差值的频次大于ECMWF，即随时效临近降水量预报逐渐增大的特征较为明显，CMA-SH9和HHUPS-ST在大部分区域小于ECMWF。

本文研究了多种模式多时效降水预报的稳定性特征，以上结论能够为模式调试以及模式产品在预报业务和决策中应用提供参考。本文未涉及模式预报的准确性，需要在后续工作中将预报准确率与稳定性结合展开探讨。