2. 河北省气象与生态环境重点实验室,石家庄 050021;
3. 河北省气象服务中心,石家庄 050021;
4. 国网河北省电力有限公司,石家庄 050011
2. Key Laboratory of Meteorological and Ecological Environment of Hebei Province, Shijiazhuang 050021;
3. Hebei Meteorological Service Center, Shijiazhuang 050021;
4. State Grid Hebei Electric Power Supply Co., Ltd., Shijiazhuang 050011
在全球变暖的大背景下,极端高温事件频发给电网负荷调度带来巨大压力(付桂琴等,2015;任永建等,2020;吴向阳和张海东,2008;郑贤等,2008;兰辉等,2021)。随着我国经济和人民生活水平的快速提升,夏季以空调为主的降温负荷在地区负荷的占比达3~5成,成为夏季用电主要负荷,然而气象条件的变化直接影响降温负荷设备的启停,日峰降温电力负荷(以下简称日峰降温负荷)问题已成为影响电力供求平衡的重要因素,当前准确预测城市降温负荷成为电力部门的一大难点,准确、定量地研究日峰降温负荷与气象因子的关系,无疑对精准预报降温负荷有帮助,同时也是电力气象服务的迫切需求。
目前关于降温负荷预测研究主要集中在两个方面:一是夏季降温负荷与气象要素的相关性研究(Selakov et al,2014;楚成博等,2013;Deihimi et al,2013;罗慧等,2016;高赐威等,2015;童述林和文福拴,2010),该类研究通常采用基准负荷比较法、最大负荷比较法、非线性回归等统计方法,在相同基准负荷值或曲线条件下估算降温负荷曲线,并讨论不同气象要素对日最大降温负荷的影响,虽然统计分析法能在一定程度上定量分析气象要素对降温负荷的影响,普适性较强,但存在一些亟待解决的通用问题,如在日降温负荷的分解研究中,未考虑基准负荷存在周期性和增长性;二是建立降温负荷与气象因子预测或评估模型(陈海燕等,2006;谢敏等,2017),该类研究多以运用相关分析、回归分析、方差分析、旋转经验正交函数和BP人工神经网络等方法,将日降温负荷与气温之间建立明确函数式,能够解决电网关注的温度升高1℃对降温负荷的影响,但未将不确定因子、节假日效应等引起的基准负荷变化考虑在内,也未综合考虑温度、湿度、风力等气象因素的影响,在实际电网气象服务中预测的降温负荷的准确度还有待提高。当前表征多个气象要素共同影响的综合指标在夏季日最大电力负荷研究方面已有应用,被证明与电力负荷具有更高的关联度(尹炤寅等,2017;杜翼等,2013;张伟,2013),但在逐日日峰降温负荷剥离阶段的应用仍鲜见报道,当前许多研究定量衡量降温负荷变幅的出发点仍为单一气象因子,因此,有必要扩展综合温度、湿度等要素的人体舒适度指标的应用领域,并定量分析其对日峰降温负荷的影响。
基于石家庄地区逐15分钟电力负荷资料及同期气象资料,考虑日峰降温负荷受经济、人类生产活动、气象等多方面因素影响,且各因素作用占比在当前信息背景下是不全面、不充分的,因此日峰降温负荷预测系统为“小样本、缺信息”的灰色系统,所以利用灰色模型、滤波法,同时考虑相同时刻日基准负荷是具有稳定发展趋势的时间序列和不确定因子、节假日效应作用,求得石家庄夏季逐15分钟逐日基准负荷,从而将降温负荷进行剥离,引入人体舒适度指标温湿指数,通过相关分析法和分段回归法得到日峰降温负荷预报模型,实现了逐日计算和发布日峰降温负荷的预报产品,为电力部门“迎峰度夏”和提高能源利用效率提供参考依据。
1 资料及方法研究中电力资料源自国网河北省电力有限公司,为2017年1月至2019年12月逐日石家庄市逐15分钟电力负荷;气象数据源自河北省气象信息中心,气象因子包括逐日最高气温、最低气温、平均气温、10分钟平均风速、平均相对湿度、日累计降水量等。同时引入用来表征夏季人体舒适度指标的有效温度和温湿指数(也称不适指数),人体舒适度指标是从气象学角度评价人体在不同气候条件下舒适感的一项生物气象指标(韩玮等,2013;胡毅等,2005)。在夏季气象因子对电力负荷峰值影响的研究中,有效温度和温湿指数等人体舒适度指标被认为比单纯的气象因子具有指示意义(曹磊和祖蓓, 2011)。
1.1 有效温度定义相对湿度、环境气温与风作用组合到一起的空气的热感觉相同的饱和湿空气温度为室外有效温度(Te),计算公式为(徐大海和朱蓉,2000;刘思捷等, 2016):
| $ \begin{array}{c} T_{\mathrm{e}}=37- \\ \frac{37-T_{\mathrm{a}}}{0.68-0.14 R_{\mathrm{h}}+\left[1 /\left(1.76+1.4 V^{0.75}\right)\right]}- \\ 0.29 T_{\mathrm{a}}\left(1-R_{\mathrm{h}}\right) \end{array} $ | (1) |
式中: Te、Ta分别为有效温度和日平均气温(单位:℃),Rh为日平均相对湿度(单位:%),V为日平均风速(单位:m·s-1)。
1.2 温湿指数温湿指数(DI)为考虑气温、湿度对人体舒适度影响的指标,又称不适指数(尹炤寅等,2017;李兴荣等,2010),计算公式为:
| $ D_{\mathrm{I}}=T-0.55\left(1-R_{\mathrm{h}}\right)(T-58) $ | (2) |
| $ T=1.8 T_{\mathrm{a}}+32 $ | (3) |
式中:T为气温(单位:℉),由式(2)和式(3)最终得到DI:
| $ D_{\mathrm{I}}=1.8 T_{\mathrm{a}}-0.55\left(1.8 T_{\mathrm{a}}-26\right)\left(1-R_{\mathrm{h}}\right)+32 $ | (4) |
灰色模型GM(1, 1)是通过因素之间的关联分析,对原始数据进行生成处理寻找变化规律,构建有规律性数据序列,建立微分方程进行预测。模型可对少量的、杂乱无章的原始数据寻找内在趋势,每次预测均对模型做一次修正, 即预测值在动态过程中产生,可揭示出系统内部事物连续发展变化周期,模型预测精度高。
由于每日同一时刻的电力负荷为具有稳定发展趋势的时间序列,同时需考虑基准负荷存在的周期性和增长性,为准确剥离石家庄市夏季(6—8月)工作日的日峰降温负荷,本文以2017—2019年石家庄市逐15分钟电力负荷资料及同期国家站数据,采用一阶一元灰色模型GM(1, 1)建模(邓聚龙,1986;李晓梅等,2004),预测2017—2019年6—8月石家庄市所有工作日的基准负荷曲线。
3 降温负荷剥离 3.1 石家庄市日峰负荷变化特征图 1为2017—2019年石家庄市日峰负荷变化情况。由图可见,石家庄市日峰负荷具有明显季节变化特征,夏季为一年中电力负荷峰值区,3年来逐日用电负荷极值和平均值呈波动中整体逐步增长趋势,其中,在7—8月达到最大值且远高于其他月份,2月春节前后电力负荷最小。3年来石家庄市平均日峰负荷为5839.17 kW,最小值为4056.04 kW,出现在2017年1月28日;最大值为8697.97 kW,出现在2019年7月28日。当前电网负荷中空调等降温负荷占比日益增大,因此定量分析夏季日峰负荷与气温因子的相关性尤为重要。
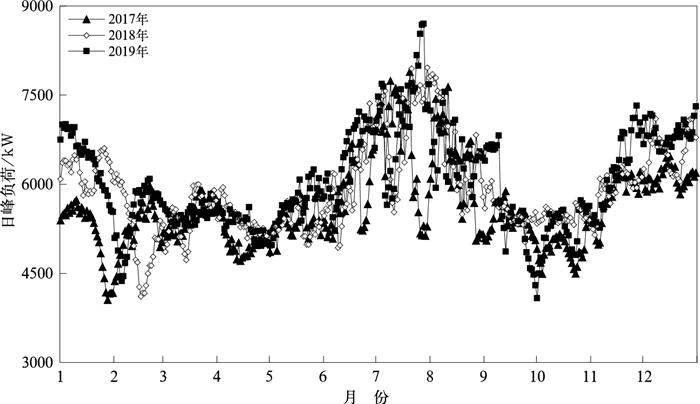
|
图 1 2017—2019年石家庄市日峰负荷曲线 Fig. 1 Daily peak load curve of Shijiazhuang from 2017 to 2019 |
图 2为选取的2018年石家庄市各季节典型负荷日变化曲线。由图可见,石家庄市负荷高峰出现的时间段季节差异明显,其中春秋冬季出现明显的双峰,而夏季负荷高峰出现在11:00—22:00,这主要是与夏季工作日的上下班时间有关。根据2017—2019年石家庄市逐15分钟电力负荷原始数据统计可知,春季日峰负荷出现在11:00—11:45和18:00—19:30的概率分别为55.07%、37.32%,夏季日峰负荷出现在11:00—12:00和17:00—18:45的概率分别为57.65%、17.26%,秋季日峰负荷出现在17:15—18:45的概率为89.74%,冬季日峰负荷出现在17:15—18:45的概率为87.41%。由于夏季与秋冬季日峰负荷出现时刻差异较大,因此以目前常用的最大负荷比较法进行降温负荷分离,即利用夏季日峰负荷与秋冬季的日峰负荷平均值的差值求得夏季日峰降温负荷明显不合理。
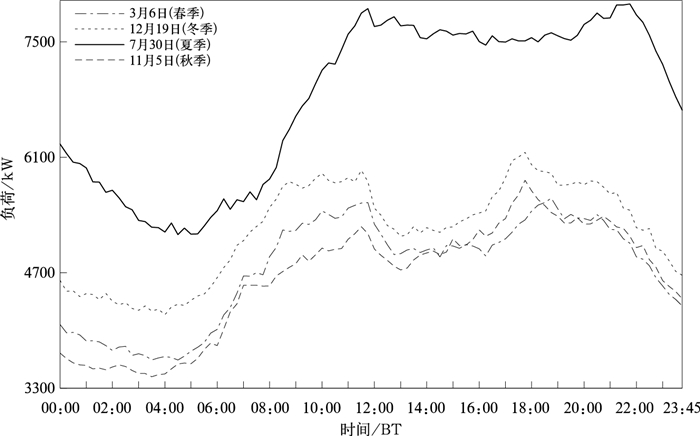
|
图 2 2018年石家庄市各季节典型负荷日变化曲线 Fig. 2 Daily variation curve of typical load in each season in Shijiazhuang in 2018 |
日负荷曲线受基准负荷、气象因素敏感度高的降温负荷以及不确定因子等方面的影响。相同时刻日基准负荷为具有稳定发展趋势的时间序列,且随社会经济发展、用电结构呈现增长性和周期性特征,为准确将石家庄市夏季(6—8月)工作日降温负荷从逐日电力负荷曲线中剥离,合理分析降温负荷特征及影响因子,本研究以2017—2019年石家庄市日用电负荷和国家级气象站数据,以剔除节假日、有降水日和Tmax>27℃后的4月上旬至5月中旬无降温负荷日的逐15分钟原始数据,建立灰色系统模型GM(1, 1)预测石家庄市2017—2019年6—8月所有工作日逐日基准负荷曲线,图 3为利用GM(1, 1)模型得出的2017年石家庄市夏季部分工作日的基准负荷曲线,经与对应日的负荷曲线比较发现变化趋势相近,基准负荷峰值出现在16:00—18:00,且8月峰值大小依次高于7月和6月,即夏季基准负荷峰值呈逐月稳定增长趋势。
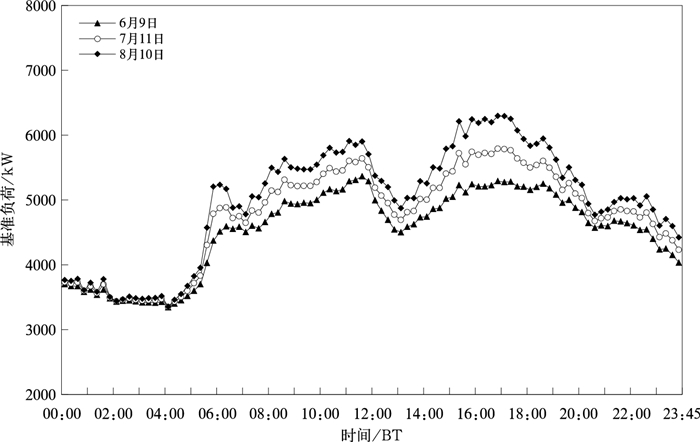
|
图 3 2017年石家庄市夏季部分工作日基准负荷曲线 Fig. 3 Benchmark load curve of some work days in summer of Shijiazhuang in 2017 |
2017—2019年石家庄市夏季(6—8月)的工作日降温负荷曲线,可由逐15分钟电力负荷减去对应时刻的基准负荷和不确定因子负荷变化而得。值得注意的是,为更好地反映出石家庄市夏季日降温负荷与气象因子的响应关系,本文在相关分析中不仅计算了日基准负荷曲线,同时将不确定因子引起的负荷变化考虑在内,即对剥离基准负荷后的日负荷曲线进行滤波,设定滤波阈值为10 d,滤波后仅保留小于10 d的高频变化,即将其视为降温负荷曲线,然后再计算日峰降温负荷与有效温度、温湿指数的相关性,以减少政府决策、重大活动保障等不确定因子影响引起的异常值对模型误差的影响,最大限度反映日峰降温负荷变率对气象条件变化的敏感度。图 4为剥离出的2017年石家庄市夏季部分工作日的降温负荷曲线,可见日降温负荷曲线整体呈W型分布,2个峰值分别出现在12:30和20:00左右,2个谷值分别出现在07:00和17:00左右。这与石家庄市日电力负荷构成、气象条件和居民生产生活等有着密切关系,07:00左右城镇居民起床后会关闭空调、开窗通风,所以降温负荷较小,07:00后居民开始上班,生活和工业空调等设备用电负荷均迅速增大,至12:00—13:00达到日最高气温,降温负荷达到峰值;17:00—18:00由于错峰上下班,降温负荷较小,19:00之后居民空调等降温设备使用量增大,降温负荷大幅上升,达到第二个峰值。

|
图 4 2017年石家庄市夏季部分工作日的降温负荷曲线 Fig. 4 Cooling load curve of some working days in summer of Shijiazhuang in 2017 |
日峰降温负荷可由日降温负荷曲线峰值得到,据统计,2017—2019年石家庄市夏季工作日的日峰降温负荷与日峰负荷比值如表 1所示,两者比值主要集中在35%以下,2017—2019年分别占当年夏季工作日天数的85.4%、62.8%、79.1%,达到35%以上的比值在14.6%~37.2%,其中比值最大值为2019年的46.63%。
|
|
表 1 2017—2019年石家庄市夏季工作日日峰降温负荷在日峰负荷中占比分布 Table 1 Distribution of daily cooling load in daily peak load of summer work days in Shijiazhuang from 2017 to 2019 |
相关系数是反映变量间变化关系密切程度的一个统计指标,其绝对值越大,表示相关性越强,两者越接近于线性关系。为避免其他气象因子的影响,选取无降水的工作日为研究对象,计算2017—2019年石家庄市夏季(6—8月)工作日的日峰降温负荷与有效温度、温湿指数之间的相关系数,分别为0.83和0.87,可见日峰降温负荷与有效温度、温湿指数之间相关性很强。
5 日峰降温负荷预测模型 5.1 日峰降温负荷与有效温度回归预测模型以2017—2019年石家庄市夏季(6—8月)剥离出的降温负荷(Pmax)与有效温度做拟合,得到3种日峰降温负荷回归预测模型:
一次函数拟合:
| $ P_{\max }=295 T_{\mathrm{e}}+5085 $ | (5) |
二次函数拟合:
| $ P_{\max }=5.5 T_{\mathrm{e}}^2+30.6 T_{\mathrm{e}}+1953.9 $ | (6) |
分段函数拟合
| $\begin{array}{c} P_{\max }=\\ \left\{\begin{array}{l} 29.5\left(T_{\mathrm{e}}-26.2\right)^2+491.1\left(T_{\mathrm{e}}-26.2\right)+ \\ \;\;\;\;\;\;\;\;2891.08 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;T_{\mathrm{e}} \leqslant 26.2^{\circ} \mathrm{C} \\ -118.7\left(T_{\mathrm{e}}-26.2\right)^2+248.9\left(T_{\mathrm{e}}-26.2\right)+ \\ \;\;\;\;\;\;\;\;2891.08 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;T_{\mathrm{e}}>26.2^{\circ} \mathrm{C} \end{array}\right. \end{array} $ | (7) |
利用2017—2019年的河北石家庄市逐15分钟电力负荷数据和考虑温度、湿度、风速等要素的同期有效温度,分别进行一次函数、二次函数、分段函数拟合(图 5),对夏季日峰降温负荷预报进行建模,同时应用2020年夏季(6—8月)工作日的日峰降温负荷与有效温度进行检验,发现3种预测模型中分段函数预测精度较高,误差在-5%~5%所占比例为57.1%,误差在-10%~10%所占比例为90.5%,与一次、二次函数拟合比较,分段函数平均相对误差减小(表 2),较准确地反映出了日最大降温负荷与有效温度的拟合关系,且有效温度在26.2℃时为预测模型的分段点。
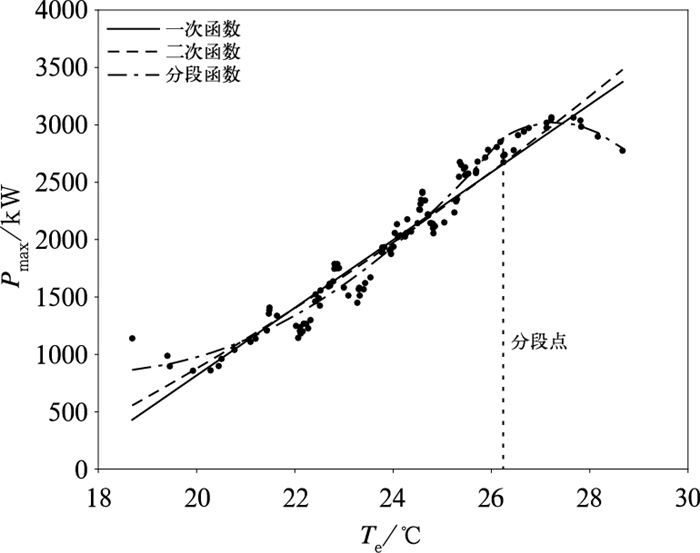
|
图 5 日峰降温负荷与有效温度的3种回归预测模型拟合曲线 Fig. 5 Fitting curve of three regression prediction models for daily peak cooling load and effective temperature |
|
|
表 2 有效温度与日峰降温负荷3种回归预测模型的相对误差及其所占比例(单位:%) Table 2 Relative errors and its proportion of three regression prediction models for effective temperature and daily peak cooling load (unit: %) |
以2017—2019年石家庄市夏季(6—8月)剥离出的降温负荷与温湿指数做拟合,得到3种日峰降温负荷回归预测模型:
一次函数拟合:
| $ P_{\max }=212 D_1-14529.8 $ | (8) |
二次函数拟合:
| $ P_{\max }=3.04 D_1^2+686.2 D_1-33006.3 $ | (9) |
分段函数拟合:
| $ \begin{array}{c} P_{\max }= \\ \left\{\begin{array}{l} 63.02\left(D_{\mathrm{I}}-75.86\right)^2+344.0\left(D_{\mathrm{I}}-75.86\right)+ \\ \;\;\;\;\;\;1404.26 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;D_{\mathrm{I}} \leqslant 75.86 \\ -18.15\left(D_{\mathrm{I}}-75.86\right)^2+346.3\left(D_{\mathrm{I}}-75.86\right)+ \\ \;\;\;\;\;\;1404.26 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;D_{\mathrm{I}}>75.86 \end{array}\right. \end{array} $ | (10) |
利用2017—2019年的河北石家庄市逐15分钟电力负荷数据和考虑温度、湿度要素的温湿指数,对夏季日峰降温负荷预报进行建模,同时应用2020年夏季(6—8月) 工作日的日峰降温负荷与温湿指数进行检验,经检验发现3种模型中分段函数预测精度较高(图 6),误差在-5%~5%所占比例为55.1%,误差在-10%~10%所占比例为88.1%,与一次、二次函数拟合比较,分段函数平均相对误差减小(表 3),较准确地反映出了日最大降温负荷与温湿指数的拟合关系,且温湿指数在75.86%时为预测模型的分段点。
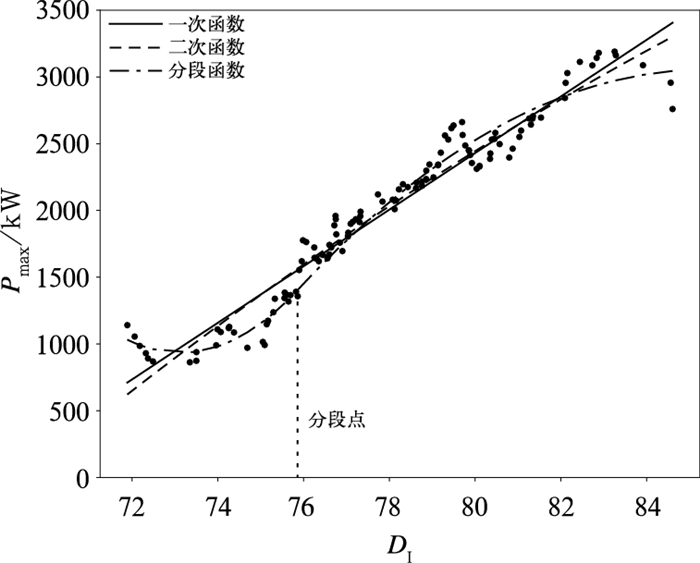
|
图 6 日峰降温负荷与温湿指数3种回归预测模型拟合曲线 Fig. 6 Fitting curve of three regression prediction models of daily peak cooling load and temperature-humidity index |
|
|
表 3 温湿指数与日峰降温负荷3种回归预测模型的相对误差及其所占比例(单位:%) Table 3 Relative error and its proportion of three regression prediction models for temperature-humidity index and daily peak cooling load (unit: %) |
(1) 石家庄电力负荷具有明显的逐年增长趋势,夏季为一年中电力负荷峰值区,剥离出的日降温负荷曲线呈W型分布,其中7—8月达到峰值且远高于其他月份,日峰负荷随季节变化明显。
(2) 提出了将有效温度和温湿指数等综合指标作为影响夏季日峰降温负荷的主要因素,以灰色系统模型GM(1, 1)进行逐日基准负荷预测,同时采用滤波法设置阈值为10 d分解出降温负荷曲线,将分离出的日峰降温负荷与有效温度和温湿指数做拟合,得到日峰降温负荷回归预测模型。
(3) 相较于考虑温度、湿度的温湿指数,有效温度综合温、湿、风共同作用,建立的夏季日峰降温负荷预测模型预测准确率更高,回归模型分段点为26.2℃,误差在-5%~5%所占比例为57.1%,误差在-10%~10%所占比例为90.5%,该夏季日峰降温负荷模型可以较好地预报出日峰降温负荷。
曹磊, 祖蓓, 2011. 夏季温湿指数与气象敏感电力负荷的研究[J]. 现代电力, 28(5): 41-45. Cao L, Zu B, 2011. Research on summer temperature-humidity index and weather sensitive electric load[J]. Mod Electr Power, 28(5): 41-45 (in Chinese). DOI:10.3969/j.issn.1007-2322.2011.05.009
|
陈海燕, 周剑波, 骆月珍, 等, 2006. 浙江盛夏降温用电负荷评估模型研究[J]. 气象科技, 34(6): 758-762. Chen H Y, Zhou J B, Luo Y Z, et al, 2006. Evaluation model of electricity loads in midsummer in Zhejiang Province[J]. Meteor Sci Technol, 34(6): 758-762 (in Chinese). DOI:10.3969/j.issn.1671-6345.2006.06.023
|
楚成博, 刘继东, 张利, 等, 2013. 山东电网夏季降温负荷特性及影响因素分析[J]. 电力需求侧管理, 15(1): 20-24. Chu C B, Liu J D, Zhang L, et al, 2013. Studies on temperature-lowering load regional characteristics of Shandong power network[J]. Power Demand Side Manage, 15(1): 20-24 (in Chinese). DOI:10.3969/j.issn.1009-1831.2013.01.006
|
邓聚龙, 1986. 灰色预测与决策[M]. 武汉: 华中理工大学出版社: 97-148. Deng J L, 1986. Grey Forecast and Decision-Making[M].
Wuhan: Huazhong University of Technology Press: 97-148 (in Chinese).
|
杜翼, 方鸽飞, 王玉芬, 2013. 考虑气象信息的短期负荷预测[J]. 华东电力, 41(5): 1051-1055. Du Y, Fang G F, Wang Y F, 2013. Short-term load forecasting considering weather factors[J]. East China Electr Power, 41(5): 1051-1055 (in Chinese).
|
付桂琴, 尤凤春, 曹欣, 等, 2015. 积温效应在电力日峰谷负荷中的应用及检验[J]. 应用气象学报, 26(4): 492-499. Fu G Q, You F C, Cao X, et al, 2015. Application and verification of accumulated temperature effects on daily peak load and daily valley load of power[J]. J Appl Meteor Sci, 26(4): 492-499 (in Chinese).
|
高赐威, 李倩玉, 苏卫华, 等, 2015. 短期负荷预测中考虑积温效应的温度修正模型研究[J]. 电工技术学报, 30(4): 242-248. Gao C W, Li Q Y, Su W H, et al, 2015. Temperature correction model research considering temperature cumulative effect in short-term load forecasting[J]. Trans China Electrotech Soc, 30(4): 242-248 (in Chinese). DOI:10.3969/j.issn.1000-6753.2015.04.030
|
韩玮, 苏敬, 王琳, 2013. 长江三角洲城市发展与人体舒适度的关系[J]. 应用气象学报, 24(3): 380-384. Han W, Su J, Wang L, 2013. Effects of urbanization on human comfort in the Yangtze River Delta[J]. J Appl Meteor Sci, 24(3): 380-384 (in Chinese). DOI:10.3969/j.issn.1001-7313.2013.03.015
|
胡毅, 李萍, 杨建功, 等, 2005. 应用气象学: 第2版[M]. 北京: 气象出版社. Hu Y, Li P, Yang J G, et al, 2005. Applied Meteorology Specialty[M]. 2nd ed. Beijing: China Meteorological Press(in Chinese).
|
兰辉, 于佳卉, 曹经福, 等, 2021. 基于温湿效应的日用电量分段方法与预测效果初探[J]. 气象, 47(7): 872-879. Lan H, Yu J H, Cao J F, et al, 2021. Study on segmental method and prediction effect of daily electricity load based on temperature and humidity[J]. Meteor Mon, 47(7): 872-879 (in Chinese).
|
李晓梅, 周晖, 李冬梅, 2004. 夏季日峰荷与有效温度的灰色建模及灵敏度分析[J]. 电网技术, 28(14): 23-27. Li X M, Zhou H, Li D M, 2004. Grey model and sensitivity analysis of summer daily peak load and effective temperature[J]. Power System Tech, 28(14): 23-27 (in Chinese). DOI:10.3321/j.issn:1000-3673.2004.14.006
|
李兴荣, 张小丽, 隋高林, 等, 2010. 深圳夏季典型晴天不同小气候区温湿及舒适度特征[J]. 气象, 36(10): 62-66. Li X R, Zhang X L, Sui G L, et al, 2010. The characteristics of temperature, humidity and comfort index of different microclimate zones on typical clear days in Shenzhen in summer[J]. Meteor Mon, 36(10): 62-66 (in Chinese).
|
刘思捷, 张海鹏, 林舜江, 等, 2016. 夏季日最大降温负荷的估算和预测方法[J]. 电力系统保护与控制, 44(5): 75-81. Liu S J, Zhang H P, Lin S J, et al, 2016. An estimating and forecasting method for daily maximum cooling load in summer[J]. Power Syst Prot Control, 44(5): 75-81 (in Chinese).
|
罗慧, 徐军昶, 肖波, 等, 2016. 气象因子对西安城市用电量的影响研究及中长期系统化预测[J]. 气象, 42(1): 54-60. Luo H, Xu J C, Xiao B, et al, 2016. Study on the impact of weather on electricity consumption in Xi'an and its application to mid-long term prediction[J]. Meteor Mon, 42(1): 54-60 (in Chinese).
|
任永建, 熊守权, 洪国平, 等, 2020. 气象因子对夏季最大电力负荷的敏感性分析[J]. 气象, 46(9): 1245-1253. Ren Y J, Xiong S Q, Hong G P, et al, 2020. Sensitivity analysis of meteorological factors to summer maximum power load[J]. Meteor Mon, 46(9): 1245-1253 (in Chinese).
|
童述林, 文福拴, 2010. 节能减排环境下广东省年最大降温负荷的测算与分析[J]. 华北电力大学学报, 37(5): 32-37. Tong S L, Wen F S, 2010. Calculation and analysis of the annual maximum high-temperature related load in the energy saving and emission reduction environment in Guangdong Province[J]. J North China Electr Power Univ, 37(5): 32-37 (in Chinese).
|
吴向阳, 张海东, 2008. 北京市气温对电力负荷影响的计量经济分析[J]. 应用气象学报, 19(5): 531-538. Wu X Y, Zhang H D, 2008. Econometric analysis on Beijing temperature influence upon electricity load[J]. J Appl Meteor Sci, 19(5): 531-538 (in Chinese).
|
谢敏, 邓佳梁, 吉祥, 等, 2017. 基于信息熵和变精度粗糙集优化的支持向量机降温负荷预测方法[J]. 电网技术, 41(1): 210-214. Xie M, Deng J L, Ji X, et al, 2017. Cooling load forecasting method based on support vector machine optimized with entropy and variable accuracy roughness set[J]. Power Syst Technol, 41(1): 210-214 (in Chinese).
|
徐大海, 朱蓉, 2000. 人对温度、湿度、风速的感觉与着衣指数的分析研究[J]. 应用气象学报, 11(4): 430-439. Xu D H, Zhu R, 2000. The sensation of human to temperature & humility & wind speed and the clothing[J]. J Appl Meteor Sci, 11(4): 430-439 (in Chinese).
|
尹炤寅, 范进进, 陈幼姣, 等, 2017. 体感温度对夏季气象负荷率变化的影响研究——以湖北省黄石市为例[J]. 气象, 43(5): 620-627. Yin Z Y, Fan J J, Chen Y J, et al, 2017. Impact of sensible temperature on summer weather-sensitive power load rate in Huangshi City[J]. Meteor Mon, 43(5): 620-627 (in Chinese).
|
张伟, 2013. 基于人体舒适度指数的配电网短期负荷预测方法[J]. 电力系统保护与控制, 41(9): 74-79. Zhang W, 2013. A distribution short-term load forecasting based on human comfort index[J]. Power Syst Prot Control, 41(9): 74-79 (in Chinese).
|
郑贤, 唐伍斌, 贝宇, 等, 2008. 桂林电网日负荷与气象因素的关系及其预测[J]. 气象, 34(10): 96-101. Zheng X, Tang W B, Bei Y, et al, 2008. A relationship between daily load and meteorological factors for Guilin power network and forecasting[J]. Meteor Mon, 34(10): 96-101 (in Chinese).
|
Deihimi A, Orang O, Showkati H, 2013. Short-term electric load and temperature forecasting using wavelet echo state networks with neural reconstruction[J]. Energy, 57: 382-401.
|
Selakov A, Cvijetinović D, Milović L, et al, 2014. Hybrid PSO-SVM method for short-term load forecasting during periods with significant temperature variations in city of Burbank[J]. Appl Soft Comput, 16: 80-88.
|
 2024, Vol. 50
2024, Vol. 50 
